一、引言
装箱问题算法、Bin-Packing算法是一种典型的优化问题,广泛应用于物流、资源分配、内存管理等领域。
二、算法原理
Bin-Packing问题可以描述为:给定一组大小不同的物品和一个容量有限的背包,如何将物品放入背包,使得背包内物品的总价值最大,且不超过背包容量。这里的物品大小和背包容量均为整数。
Bin-Packing算法的目标是:将n个物品放入最少数量的背包中,使得每个背包的容量不超过给定值。
Bin-Packing算法是一种组合优化问题,旨在将一组物品(具有不同的大小)放入有限数量的容器(或"箱子")中,使得使用的容器数量最小化。该问题属于NP-hard问题,意味着没有已知的多项式时间算法可以解决所有实例。
三、数据结构
物品:一个物品包含两个属性,分别是大小和编号。
背包:一个背包包含一个属性,即当前已装入物品的总大小。
- 数组:用于存储物品的大小。
- 列表:用于存储每个容器中物品的分配情况。
- 堆:用于实现最佳适应算法时的快速查找。
四、算法使用场景
Bin-Packing算法的应用场景包括:
- 内存管理:操作系统在内存分配时需要将进程的内存需求放入可用内存块中。
- 物流与运输:在运输过程中,将货物装载到卡车或集装箱中。
-
云计算:在云服务中,合理分配虚拟机资源。
-
**仓库存储:**将不同规格的货物放入仓库,使得仓库空间利用率最高。
**虚拟机调度:**将多个虚拟机分配到物理服务器上,使得服务器资源利用率最高。
五、算法实现
Bin-Packing算法有多种实现方式,以下介绍两种常见的算法:
贪心算法(First Fit) (1)将物品按大小从小到大排序。 (2)遍历每个物品,将其放入第一个能容纳它的背包中。 (3)如果所有背包都无法容纳该物品,则创建一个新的背包。
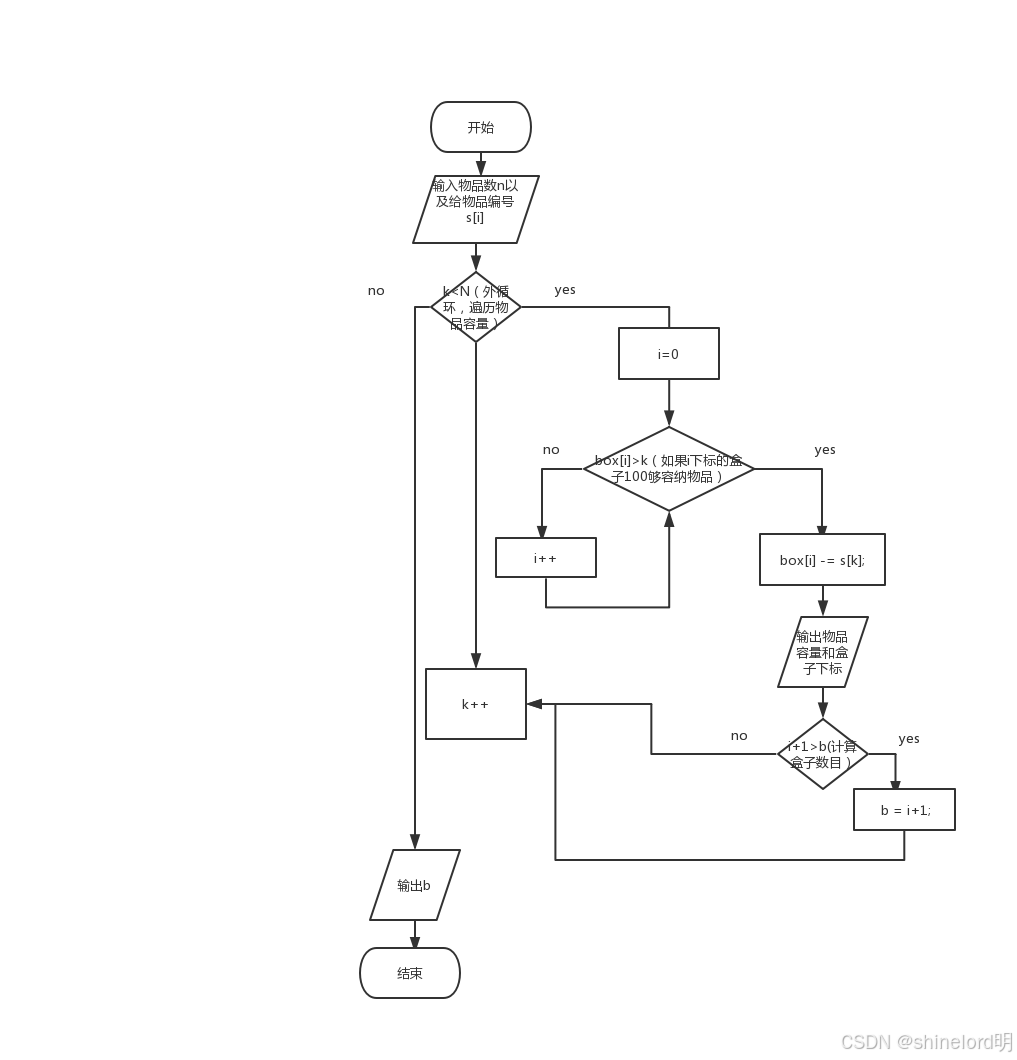
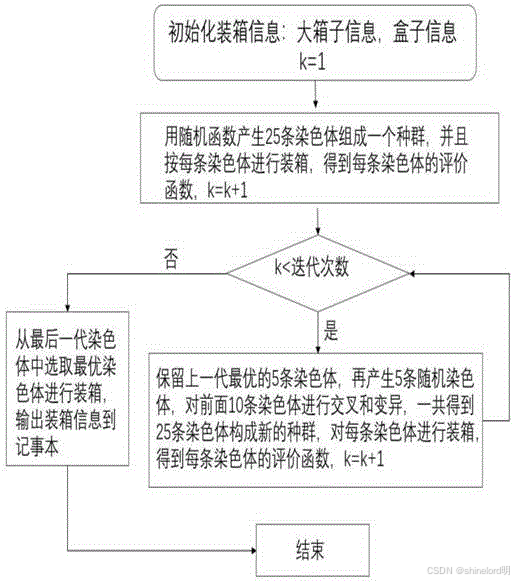
动态规划算法(Best Fit) (1)将物品按大小从小到大排序。 (2)遍历每个物品,找到能容纳它且剩余空间最小的背包。 (3)将物品放入该背包,更新背包的剩余空间。
六、其他同类算法对比
- First Fit:按顺序放入第一个合适的容器。
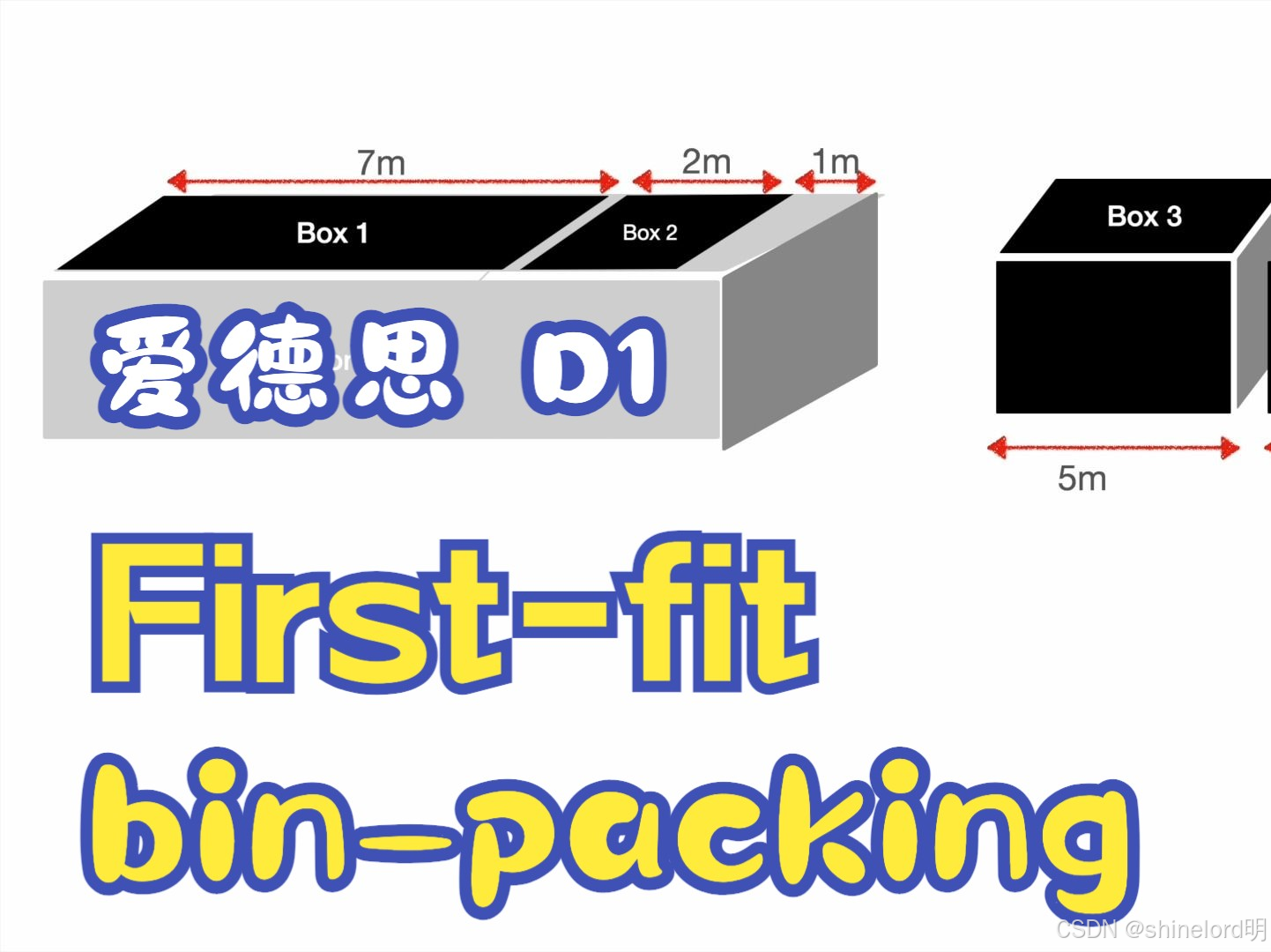
- Best Fit:放入能够容纳剩余空间最小的容器。
- Next Fit:在上一个容器无法放入时,尝试放入新的容器。
- Worst Fit:放入剩余空间最大的容器。
- 贪心算法:Bin-Packing问题的贪心算法通常表现良好,但不能保证找到最优解。相较于动态规划,贪心算法实现简单且效率高。
- 动态规划:可以找到最优解,但时间复杂度较高,适合物品数量和箱子数量较小的情况。
- 回溯算法:通过尝试所有可能的组合来找到最优解,适合小规模问题,但效率低下。
七、多语言实现
Java
java
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class BinPacking {
public static List<List<Integer>> firstFit(int[] items, int binCapacity) {
List<List<Integer>> bins = new ArrayList<>();
for (int item : items) {
boolean placed = false;
for (List<Integer> bin : bins) {
int binWeight = bin.stream().mapToInt(Integer::intValue).sum();
if (binWeight + item <= binCapacity) {
bin.add(item);
placed = true;
break;
}
}
if (!placed) {
List<Integer> newBin = new ArrayList<>();
newBin.add(item);
bins.add(newBin);
}
}
return bins;
}
public static void main(String[] args) {
int[] items = {4, 8, 1, 4, 2, 1};
int binCapacity = 10;
List<List<Integer>> bins = firstFit(items, binCapacity);
System.out.println("Bins: " + bins);
}
}Python
python
def first_fit(items, bin_capacity):
bins = []
for item in items:
placed = False
for bin in bins:
if sum(bin) + item <= bin_capacity:
bin.append(item)
placed = True
break
if not placed:
bins.append([item])
return bins
if __name__ == "__main__":
items = [4, 8, 1, 4, 2, 1]
bin_capacity = 10
bins = first_fit(items, bin_capacity)
print("Bins:", bins)C++
cpp
#include <iostream>
#include <vector>
#include <numeric>
std::vector<std::vector<int>> firstFit(int items[], int n, int binCapacity) {
std::vector<std::vector<int>> bins;
for (int i = 0; i < n; i++) {
bool placed = false;
for (auto &bin : bins) {
if (std::accumulate(bin.begin(), bin.end(), 0) + items[i] <= binCapacity) {
bin.push_back(items[i]);
placed = true;
break;
}
}
if (!placed) {
bins.push_back({items[i]});
}
}
return bins;
}
int main() {
int items[] = {4, 8, 1, 4, 2, 1};
int binCapacity = 10;
int n = sizeof(items) / sizeof(items[0]);
auto bins = firstFit(items, n, binCapacity);
std::cout << "Bins:\n";
for (const auto &bin : bins) {
std::cout << "[ ";
for (int item : bin) {
std::cout << item << " ";
}
std::cout << "]\n";
}
return 0;
}Go
Go
package main
import (
"fmt"
)
func firstFit(items []int, binCapacity int) [][]int {
bins := [][]int{}
for _, item := range items {
placed := false
for i := range bins {
binWeight := 0
for _, bItem := range bins[i] {
binWeight += bItem
}
if binWeight+item <= binCapacity {
bins[i] = append(bins[i], item)
placed = true
break
}
}
if !placed {
bins = append(bins, []int{item})
}
}
return bins
}
func main() {
items := []int{4, 8, 1, 4, 2, 1}
binCapacity := 10
bins := firstFit(items, binCapacity)
fmt.Println("Bins:", bins)
}八、实际服务应用场景代码框架
服务框架设计
- 服务接口:提供一个API接收物品和箱子容量。
- 处理逻辑:使用Bin-Packing算法处理请求。
- 返回结果:返回每个箱子的物品分配情况。
示例代码(使用Python Flask)
python
from flask import Flask, request, jsonify
app = Flask(__name__)
def first_fit(items, bin_capacity):
bins = []
for item in items:
placed = False
for bin in bins:
if sum(bin) + item <= bin_capacity:
bin.append(item)
placed = True
break
if not placed:
bins.append([item])
return bins
@app.route('/bin-packing', methods=['POST'])
def bin_packing():
data = request.json
items = data.get('items', [])
bin_capacity = data.get('bin_capacity', 10)
bins = first_fit(items, bin_capacity)
return jsonify(bins)
if __name__ == "__main__":
app.run(debug=True)测试服务
可以使用Postman或curl发送POST请求测试服务:
rust
curl -X POST http://127.0.0.1:5000/bin-packing -H "Content-Type: application/json" -d '{"items": [4, 8, 1, 4, 2, 1], "bin_capacity": 10}'