1.1 傅里叶变换 (Fourier Transform)
介绍
傅里叶变换是一种数学变换,用于将图像从空间域转换到频率域。它广泛应用于图像去噪和滤波。
原理
傅里叶变换将图像表示为频率成分的叠加,使得频率成分可以独立处理。通过对频率成分的分析和处理,可以实现对图像的去噪、增强和其他操作。
公式
连续傅里叶变换:

离散傅里叶变换(DFT):
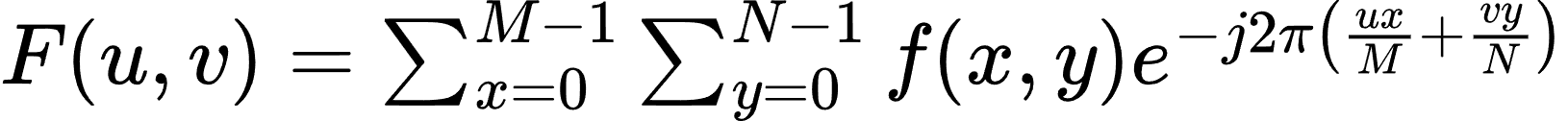
案例1
使用Python和OpenCV进行傅里叶变换。
代码解析
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('image.jpg', 0)
# 进行傅里叶变换
dft = cv2.dft(np.float32(image), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
# 计算频谱图
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))
# 显示原始图像和频谱图
plt.subplot(121), plt.imshow(image, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
案例2:低通滤波器应用
在医学图像处理中,经常使用傅里叶变换进行低通滤波,以去除图像中的噪声。
代码解析
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('image.jpg', 0)
# 进行傅里叶变换
dft = cv2.dft(np.float32(image), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
# 创建一个低通滤波器
rows, cols = image.shape
crow, ccol = rows // 2 , cols // 2
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
# 应用滤波器并逆变换
fshift = dft_shift * mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0], img_back[:,:,1])
# 显示结果
plt.subplot(131), plt.imshow(image, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(mask[:,:,0], cmap='gray')
plt.title('Mask'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(img_back, cmap='gray')
plt.title('After LPF'), plt.xticks([]), plt.yticks([])
plt.show()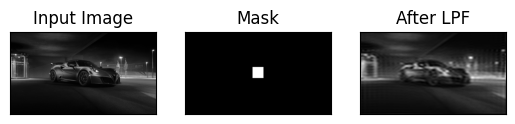
生活场景案例
傅里叶变换在图像压缩、去噪和医学成像中应用广泛。
总结
傅里叶变换将图像从空间域转换到频率域,便于频率分析和处理。
1.2 离散余弦变换 (Discrete Cosine Transform, DCT)
介绍
离散余弦变换(DCT)用于将图像分解为不同频率的余弦分量,广泛应用于图像压缩,如JPEG。
原理
DCT将图像表示为余弦函数的线性组合,有效地集中能量,使得大部分能量集中在较少的DCT系数中,便于压缩。
公式
一维离散余弦变换:
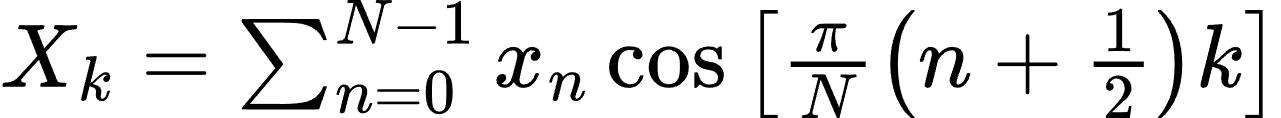
案例:JPEG图像压缩
在JPEG图像压缩中,DCT用于将图像块分解为频率成分,然后仅保留低频分量进行压缩。
代码解析
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('image.jpg', 0)
# 进行离散余弦变换
dct = cv2.dct(np.float32(image))
# 显示原始图像和DCT结果
plt.subplot(121), plt.imshow(image, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(dct, cmap='gray')
plt.title('DCT Image'), plt.xticks([]), plt.yticks([])
plt.show()
生活场景案例
DCT在JPEG图像压缩中广泛应用,通过压缩高频成分减少数据量。
总结
DCT将图像分解为余弦分量,实现能量集中和数据压缩。
1.3 小波变换 (Wavelet Transform)
介绍
小波变换用于多分辨率分析,可以在不同尺度上分析图像特征,广泛应用于图像压缩和去噪。
原理
小波变换通过小波函数将图像分解为不同尺度和位置的子带,可以有效地表示图像中的局部特征。
公式
连续小波变换:
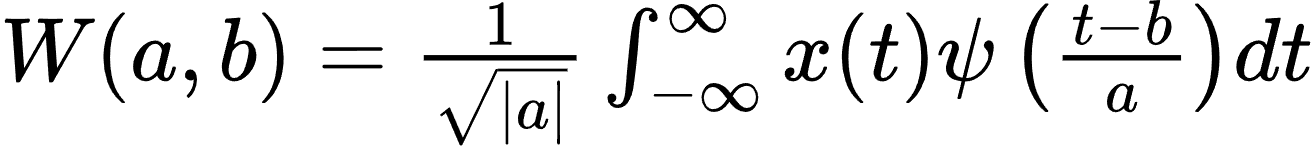
案例
使用Python和PyWavelets进行小波变换。
代码解析
python
import pywt
import cv2
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('image.jpg', 0)
# 进行小波变换
coeffs2 = pywt.dwt2(image, 'bior1.3')
LL, (LH, HL, HH) = coeffs2
# 显示结果
plt.figure(figsize=(12, 3))
titles = ['Approximation', ' Horizontal detail', 'Vertical detail', 'Diagonal detail']
for i, a in enumerate([LL, LH, HL, HH]):
plt.subplot(1, 4, i + 1)
plt.imshow(a, cmap='gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
案例2:图像去噪
小波变换可以用于图像去噪,通过分解图像,滤除高频噪声并重构图像。
代码解析
python
import pywt
import cv2
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('image.jpg', 0)
# 进行小波变换
coeffs2 = pywt.dwt2(image, 'bior1.3')
LL, (LH, HL, HH) = coeffs2
# 进行去噪处理
coeffs2_filtered = LL, (LH * 0.5, HL * 0.5, HH * 0.5)
# 重构图像
image_reconstructed = pywt.idwt2(coeffs2_filtered, 'bior1.3')
# 显示结果
plt.subplot(131), plt.imshow(image, cmap='gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(LL, cmap='gray')
plt.title('Approximation'), plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(image_reconstructed, cmap='gray')
plt.title('Denoised Image'), plt.xticks([]), plt.yticks([])
plt.show()
生活场景案例
小波变换在医学图像处理、数据压缩和去噪等领域有重要应用。
总结
小波变换通过多分辨率分析,有效处理图像中的细节和特征,实现压缩和去噪。