排序算法之堆排序

title: 堆排序

date: 2024-7-23 15:48:25 +0800

categories:

排序算法
tags:
排序
算法
堆排序
description: 堆排序（Heap Sort）是一种基于堆的排序算法，具有较高的效率和稳定性。
math: true

堆排序

堆排序（Heap Sort）是一种基于堆的排序算法，具有较高的效率和稳定性。堆排序利用堆这种完全二叉树的数据结构进行排序，常用的是大顶堆（最大堆）来实现升序排序。本文将详细介绍堆排序的原理、步骤、示例、复杂度分析及其Java代码实现。

堆排序的原理

堆的定义 ：堆是一种完全二叉树，其中每个节点的值都大于或等于其左右子节点的值，这种堆称为大顶堆；每个节点的值都小于或等于其左右子节点的值，这种堆称为小顶堆。
通常堆是通过一维[数组]来实现的。在数组起始位置为0的情形中：

父节点i的左子节点在位置 ( 2 i + 1 ) (2i+1) (2i+1);
父节点i的右子节点在位置 ( 2 i + 2 ) (2i+2) (2i+2);
子节点i的父节点在位置 ( i − 1 ) / 2 (i−1)/2 (i−1)/2;

堆排序的基本思想 ：
- 将待排序的数组构造成一个大顶堆。
- 取出堆顶元素（当前堆中最大值），将其与堆的最后一个元素交换。
- 调整堆结构，使其满足堆的性质，重复上述步骤直到整个数组排序完成。

堆排序的步骤

构建初始堆：将无序数组构建成一个大顶堆。
交换堆顶元素与末尾元素：将堆顶元素（最大值）与末尾元素交换。
调整堆：将剩余元素重新调整为大顶堆。
重复步骤2和3，直到所有元素有序。

图示

示例

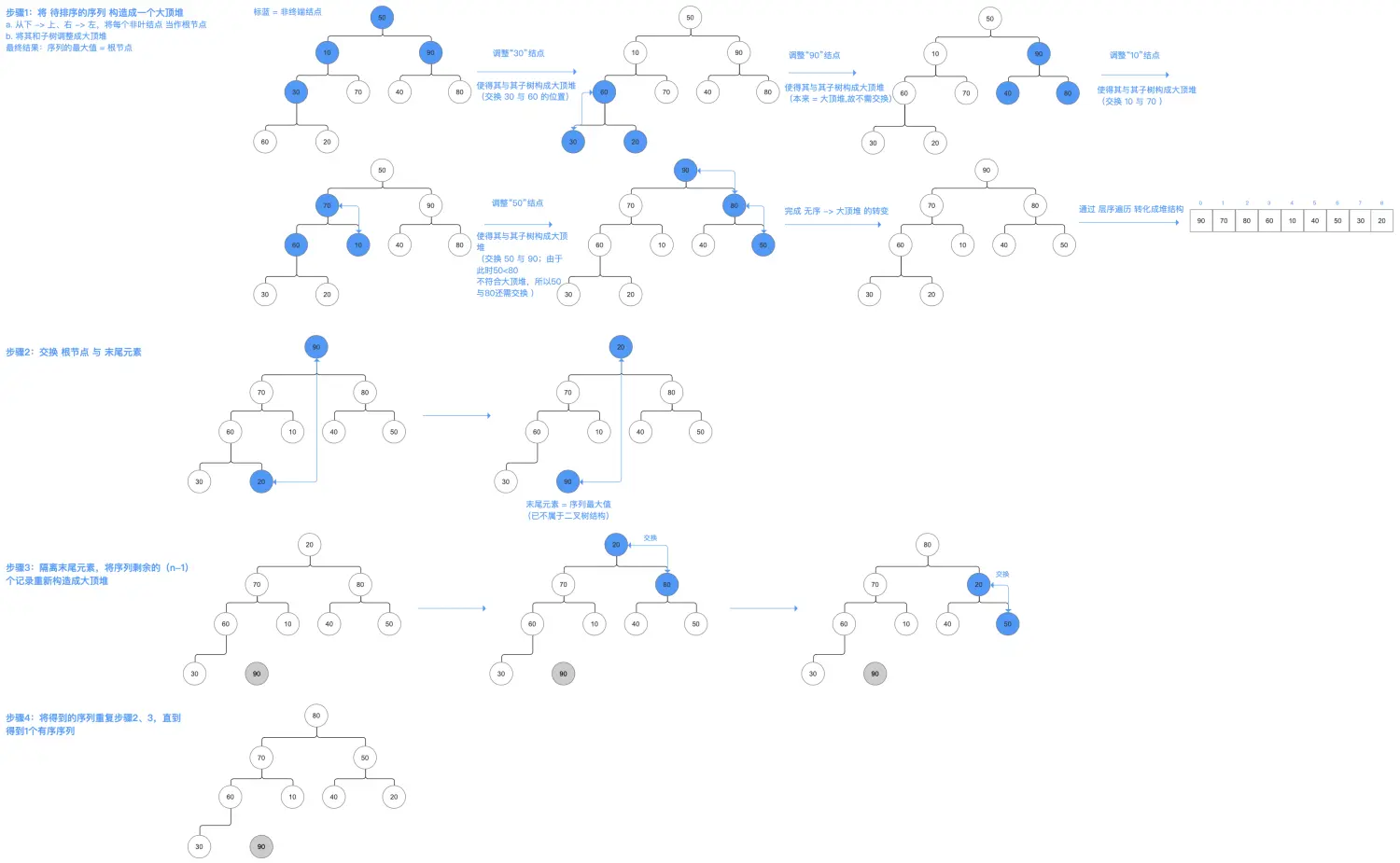
复杂度分析

时间复杂度为 O ( n log ⁡ n ) O(n \log n) O(nlogn)、非自适应排序 ：建堆操作使用 O ( n ) O(n) O(n) 时间。从堆中提取最大元素的时间复杂度为 O ( log ⁡ n ) O(\log n) O(logn) ，共循环 n − 1 n - 1 n−1 轮。
空间复杂度为 O ( 1 ) O(1) O(1)、原地排序 ：几个指针变量使用 O ( 1 ) O(1) O(1) 空间。元素交换和堆化操作都是在原数组上进行的。
非稳定排序：在交换堆顶元素和堆底元素时，相等元素的相对位置可能发生变化。

时间复杂度

所有时间复杂度 ： O ( n log ⁡ n ) O(n \log n) O(nlogn)。

空间复杂度

空间复杂度 ： O ( 1 ) O(1) O(1)

堆排序的代码实现（Java）

java 复制代码

public class HeapSort {

    // 主排序函数
    public static void heapSort(int[] arr) {
        int n = arr.length;

        // 构建初始大顶堆,从非叶子结点的元素处开始遍历
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        // 逐步将堆顶元素与末尾元素交换，并调整堆
        for (int i = n - 1; i > 0; i--) {
            // 将当前堆顶元素与末尾元素交换
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            // 调整堆
            heapify(arr, i, 0);
        }
    }

    // 调整堆
    public static void heapify(int[] arr, int n, int i) {
        int largest = i; // 当前节点
        int left = 2 * i + 1; // 左子节点
        int right = 2 * i + 2; // 右子节点

        // 如果左子节点大于当前节点，则更新最大值
        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }

        // 如果右子节点大于当前节点，则更新最大值
        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }

        // 如果最大值不是当前节点，则交换，并递归调整堆
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
			//如果交换了,需要确认被交换的叶子节点仍然是个大顶堆
            heapify(arr, n, largest);
        }
    }

    // 主函数
    public static void main(String[] args) {
        int[] arr = {38, 27, 43, 3, 9, 82, 10};
        System.out.println("Given Array:");
        for (int num : arr) {
            System.out.print(num + " ");
        }
        System.out.println();

        // 调用堆排序函数
        heapSort(arr);

        System.out.println("\nSorted Array:");
        for (int num : arr) {
            System.out.print(num + " ");
        }
        System.out.println();
    }
}