算法之动态规划
动态规划(dp)
概念:
- 将递归算法重新写成非递归算法 ,让后者把那些子问题的答案系统地记录在一个表(dp数组)内 ,这种方法叫做动态规划
- 通常用于求解具有最优性质的问题(最优子结构&最优子问题),希望找到具有最优值的解。
- 核心为穷举,动态规划问题往往具有最优子结构,重叠子问题和状态转移方程的特征。
基本思想:
- 适用于子问题不是独立的情况,也就是各子问题包含公共的子问题,鉴于会重复的求解各个子问题,对每个问题只求一遍,将其保存在一张表中,从而避免重复计算。
特征:
-
最优子结构:当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。
-
重叠子问题:在用递归算法自顶向下解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。动态规划算法利用这个子问题重叠性质,对每一个问题只解一次,而后将其解保存在一个表格(dp数组)中,在以后尽可能多地利用这些子问题的解。
-
状态转移方程(最关键):
- 是动态规划中本阶段的状态往往是上一阶段状态和上一阶段决策的结果。如果给定了第K阶段的状态Sk 以及决策uk (Sk ),则第K+1阶段的状态Sk+1也就完全确定
- 也就是递推方程,一个状态的解往往可以由前一个状态的解得出
- 状态是由自己定义的通常可以认为是函数参数,dp数组的索引。
- 状态转移 就是从一个状态变成另一个状态,就例如本质为斐波那契数列的爬楼梯问题,从N-1阶或N-2的楼梯上到N阶的楼梯就称为状态转移.
- 状态压缩 :有时候并不需要保存所有状态 ,当保存的状态减少,导致算法的空间复杂度降低的技巧叫做状态压缩
能解决的问题:
- 计数
- 最值
- 存在性(是和否的问题,例如01背包)
解题步骤:
- 明确状态 :
也就是原问题和子问题中会变化的变量,状态的种数决定dp数组的维度。根据题意定义状态,这个状态可能是求解题目会变化的量,因为动态规划本质就是穷举,所以这个状态应该是穷举所有方案能够找到求解的目标 - 明确选择 :
也就是导致状态产生变化的行为。选择就是限制,当我们需要求解问题时,就需要不断地更新选择限制中的数据,来不断地产生多个方案,从而从中找到最优方案。 - 明确dp函数/数组的定义:就是求解的问题的函数,这个函数要求什么
- base case:初始状态,根据题意找到初始状态,然后写出状态转移方程然后写出自顶向下或者自底向上递推的解法
分析问题:
- 先分析问题,用备忘录消除重叠子问题,写出自顶向下解法
- 进一步,可以写出自底向上解法
- 再进一步,可能可以优化空间复杂度
动态规划框架:
cpp
//初始化 base case
dp[0][0][...]=base;
//进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...]=求最值(选择1,选择2,...);例子:
零钱兑换问题:
分析问题:
- 设F(n)为求解凑出目标金额为n的最少硬币数,通过分析问题,求解目标金额为n的最小硬币数F(n)=min(F(n-coin1),F(n-coin2)...),当coins=[1,2,5],目标金额为11时,则F(11)=min(F(11-1),F(11-2),F(11-5)),然后依次递推下去,这样就形成了自顶向下的求法,但是会有重复计算,因此需要使用备忘录也就是记忆性递归来剪枝进行优化
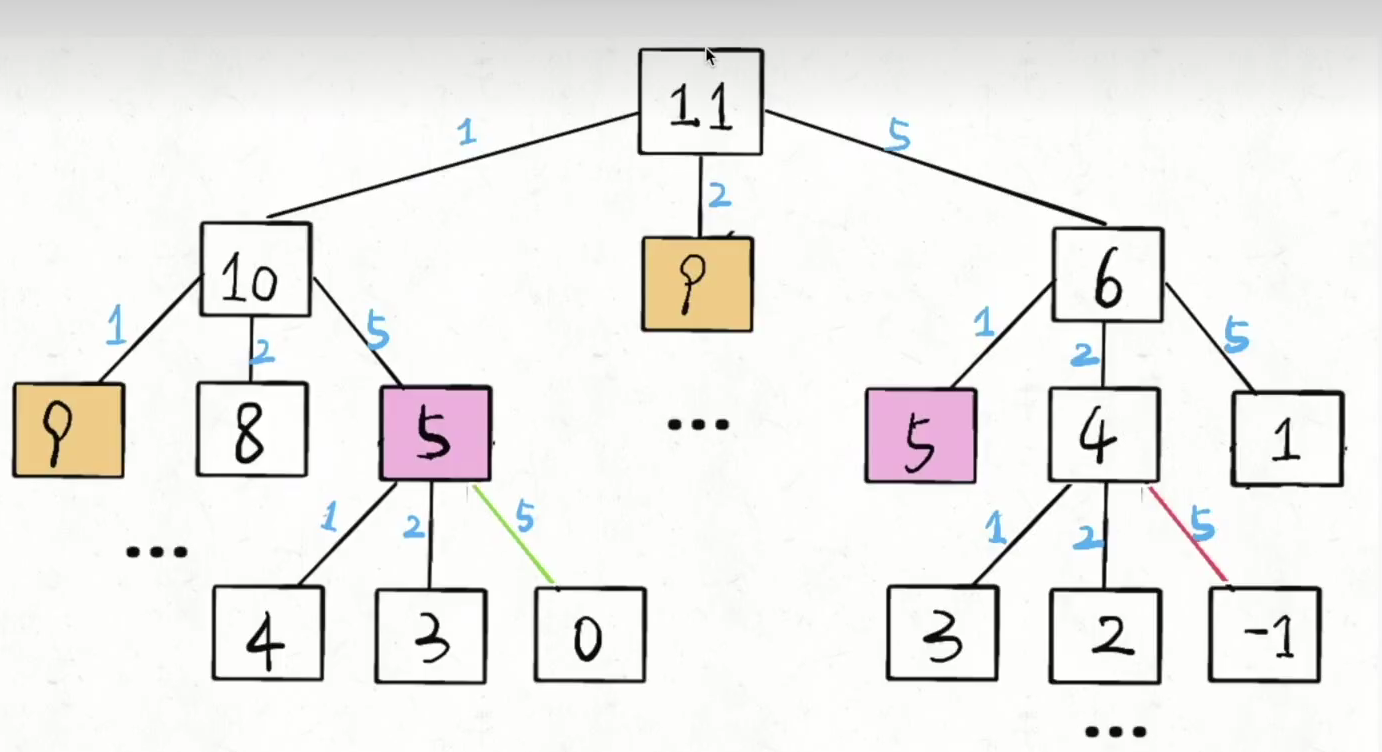
- 自顶向下解法:
cpp
class Solution {
//因为这是自顶向下递推,初始化则只需要初始化为达不到的值就行了
vector<int>v;
int dp(vector<int> coins,int amount){
if(amount==0) return 0;
if(amount<0) return -1;
if(v[amount]!=-2) return v[amount];
int res=INT_MAX;
for(int coin:coins){
int sub=dp(coins,amount-coin);
if(sub==-1) continue;
res=min(res,sub+1);
}
//存到备忘录中
v[amount]=(res==INT_MAX)?-1:res;
return v[amount];
}
public:
int coinChange(vector<int>& coins, int amount) {
v.assign(amount+1,-2);
return dp(coins,amount);
}
};- 自底向上解法:
cpp
class Solution {
public:
//状态:目标金额 amount 因为每选择一枚硬币就会导致amount数值减少
//选择:coins数组,包含着硬币面额,选择不同面额的硬币就会导致amount的不同,凑出amount的方案也不同
//函数定义:coinChange函数,对于目标金额amount,至少需要coinChange(coins,amount)枚硬币
//base case:当amount=0时,则最少需要0个硬币,当amount<0,则无法凑出目标金额
int coinChange(vector<int>& coins, int amount) {
//目标金额所用最多硬币数为amount,因为是求解最小硬币数问题,所以应该初始化比amount还大
vector<int>dp(amount+1,amount+1);
//base case
dp[0]=0;
//枚举所有状态
for(int i=0;i<amount+1;i++){
for(int j:coins){
//判断当前amount是否小于选择的面额,如果小于就跳过
if(i-j<0) continue;
//状态转移,求出凑出当前面额i的最小硬币数
dp[i]=min(dp[i],dp[i-j]+1);
}
}
return (dp[amount]>=amount+1)?-1:dp[amount];
}
};01背包问题

- 经典的动态规划题目,01背包的01就对应着我是否将当前物品放入背包中,由题意可知,我们只需要求解dp[N] [W]就可以得到答案,分析题目对于选择i物品时,当前背包剩余重量为w时,我们将物品i放入背包则dp[i] [w]=dp[i-1] [w-wt[i-1]]+val[i-1],我们不将物品i放入背包则dp[i] [w]=dp[i-1] [w],因此我们取其最大值就可以求出对于前i个物品,当背包容量为w时,可以装的最大价值,因此状态转移方程为max(dp[i-1] [w],dp[i-1] [w-wt[i-1]]+val[i-1]);
cpp
#include <iostream>
using namespace std;
//状态:背包的空余容量剩多少,可选择的物品还有哪些
//选择:把这个物品是否放进背包
//dp[i][w]定义,对于前i个物品,当背包的容量为w时,可以装的最大价值是dp[i][w]
//base case:dp[0][...]=dp[...][0]=0,因为当选择物品为0的时候无论w多少都为0,当背包容量为0时,无论物品多少都无法放进
int main(){
int N,W;
cin>>N>>W;
int val[N],wt[N];
for(int i=0;i<N;i++){
cin>>val[N]>>wt[N];
}
int dp[N+1][W+1];
memset(dp,0, sizeof(int)*((N+1)*(W+1)));
for(int i=1;i<=N;i++){
for(int w=W;w>=wt[i-1];w--){
dp[i][w]=max(dp[i-1][w],dp[i-1][w-wt[i-1]]+val[i-1]);
}
}
cout<<dp[N][W];
return 0;
}完全背包问题:
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
二维dp:
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+1;
int n,m;
int v[N],w[N],dp[N][N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i) cin>>v[i]>>w[i];
for(int i=1;i<=n;++i){
for(int j=0;j<=m;++j){
dp[i][j]=dp[i-1][j];
if(j-v[i]>=0) dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);
}
}
cout<<dp[n][m]<<endl;
return 0;
}状态压缩:
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+1;
int n,m;
int v[N],w[N],dp[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i) cin>>v[i]>>w[i];
for(int i=1;i<=n;++i){
for(int j=v[i];j<=m;++j){
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[m]<<endl;
return 0;
}