【NLP】注意力机制：规则、作用、原理、实现方式

文章目录

1、本章目标
2、注意力机制介绍
3、注意力计算规则
- 3.1、打个比喻
- 3.2、公式
- - [3.2.1、线性变换 + 点积注意力](#3.2.1、线性变换 + 点积注意力)
  - 3.2.2、加性注意力
  - 3.2.3、点积注意力
  - 3.2.4、对比与总结
  - 3.2.5、bmm运算
4、注意力机制的作用
5、注意力机制原理⭐
6、注意力机制实现步骤
7、小结

🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎人工智能和前端开发。

🦅个人主页：@逐梦苍穹

📕所属专栏：人工智能

🌻gitee地址：xzl的人工智能代码仓库

✈ 您的一键三连，是我创作的最大动力🌹

1、本章目标

了解什么是注意力计算规则以及常见的计算规则
了解什么是注意力机制及其作用
掌握注意力机制的原理
掌握注意力机制的实现步骤

下一章节详细介绍的是 Self-Attention

2、注意力机制介绍

2.1、注意力概念

我们观察事物时，之所以能够快速判断一种事物(当然允许判断是错误的)，是因为我们大脑能够很快把注意力放在事物最具有辨识度的部分从而作出判断，而并非是从头到尾的观察一遍事物后，才能有判断结果。

正是基于这样的理论，就产生了注意力机制

2.2、注意力机制

注意力机制（Attention Mechanism）是现代深度学习，特别是自然语言处理（NLP）和计算机视觉领域中的关键技术，是注意力计算规则能够应用的深度学习网络的载体, 同时包括一些必要的全连接层以及相关张量处理, 使其与应用网络融为一体

其核心思想是模拟人类视觉注意力的机制，即在处理大量信息时，可以集中注意力在最相关的部分，而忽略不太重要的信息。
使用自注意力计算规则的注意力机制称为自注意力机制

NLP领域中, 当前的注意力机制大多数应用于seq2seq架构, 即编码器和解码器模型

传统的序列模型（如RNN和LSTM）在处理长序列时存在困难，因为它们倾向于遗忘早期输入的信息。

注意力机制通过允许模型在每个时间步都"注意"整个输入序列的不同部分，从而有效解决了这个问题。

这种机制最早在机器翻译中被引入（如Bahdanau等人提出的机制），但现在已经广泛应用于各种NLP任务和其他领域

2.3、翻译举例

如果你在翻译网站上面依次输入"I love the 2022 Beijing Winter Games"，你会看到实时变化的翻译结果，这个结果会随着你输入的完整，而逐渐趋于正确。

只考虑games，则是游戏或比赛；beijin+games，则翻译为比赛更合理；

当2022+beijin+winter+games，翻译为冬奥会就是非常准确的了。

3、注意力计算规则

它需要三个指定的输入Q(query)，K(key)，V(value)，然后通过计算公式得到注意力的结果，

这个结果代表query在key和value作用下的注意力表示；

当输入的Q=K=V时，称作 自注意力计算规则 。

3.1、打个比喻

Q, K, V的比喻解释：

假如我们有一个问题：给出一段文本，使用一些关键词对它进行描述

为了方便统一正确答案，这道题可能预先已经给大家写出了一些关键词作为提示

其中这些给出的提示就可以看作是key，

而整个的文本信息就相当于是query，

value的含义则更抽象，可以比作是你看到这段文本信息后，脑子里浮现的答案信息

这里我们又假设大家最开始都不是很聪明 ，

第一次看到这段文本后脑子里基本上浮现的信息就只有提示这些信息，
因此key与value基本是相同的 ，但是随着我们对这个问题的深入理解，通过我们的思考脑子里想起来的东西原来越多，并且能够开始对我们query也就是这段文本，提取关键信息进行表示。

这就是注意力作用的过程，通过这个过程，我们最终脑子里的value发生了变化，根据提示key生成了query的关键词表示方法，也就是另外一种特征表示方法

刚刚我们说到key和value一般情况下默认是相同，与query是不同的，这种是我们一般的注意力输入形式，

但有一种特殊情况，就是我们query与key和value相同，这种情况我们称为 自注意力机制 ；

就如同我们的刚刚的例子，使用 一般注意力机制 ，是使用不同于给定文本的关键词表示它；

而 自注意力机制 ，需要用给定文本自身 来表达自己，也就是说你需要从给定文本中抽取关键词来表述它，相当于对文本自身的一次特征提取。(下一篇文章讲这个自注意力机制)

3.2、公式

3.2.1、线性变换 + 点积注意力

公式：
Attention ( Q , K , V ) = Softmax ( Linear ( [ Q , K ] ) ) ⋅ V \text{Attention}(Q, K, V) = \text{Softmax}(\text{Linear}([Q, K])) \cdot V Attention(Q,K,V)=Softmax(Linear([Q,K]))⋅V

这个公式描述了一个基于线性变换和点积的注意力机制。

步骤如下：

线性变换 ：将查询 Q Q Q 和键 K K K 拼接后，通过一个线性层（即全连接层）进行变换。这个过程可以捕捉到查询和键之间的线性关系。
点积注意力：对变换后的结果进行softmax操作，得到注意力权重。
加权和 ：用注意力权重对值 V V V 进行加权和。

3.2.2、加性注意力

公式：
Attention ( Q , K , V ) = Softmax ( sum ( tanh ⁡ ( Linear ( [ Q , K ] ) ) ) ) ⋅ V \text{Attention}(Q, K, V) = \text{Softmax}(\text{sum}(\tanh(\text{Linear}([Q, K])))) \cdot V Attention(Q,K,V)=Softmax(sum(tanh(Linear([Q,K]))))⋅V

这个公式描述了一个基于tanh激活函数和线性变换的注意力机制，通常称为加性注意力（Additive Attention）。步骤如下：

线性变换 ：将查询 Q Q Q 和键 K K K 拼接后，通过一个线性层进行变换。
激活函数：对变换后的结果应用tanh激活函数，这可以捕捉到非线性关系。
加性注意力：对经过激活函数处理的结果进行求和，再通过softmax操作得到注意力权重。
加权和 ：用注意力权重对值 V V V 进行加权和。

3.2.3、点积注意力

公式：
Attention ( Q , K , V ) = Softmax ( Q ⋅ K T d k ) ⋅ V \text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{Q \cdot K^T}{\sqrt{d_k}}\right) \cdot V Attention(Q,K,V)=Softmax(dk Q⋅KT)⋅V

这个公式是标准的缩放点积注意力（Scaled Dot-Product Attention），是Transformer模型中的核心机制。

步骤如下：

点积：计算查询 Q Q Q 和键 K K K 的点积。
缩放：将点积结果除以键向量的维度的平方根 d k \sqrt{d_k} dk ，以防止值过大。
softmax：对缩放后的结果进行softmax操作，得到注意力权重。
加权和 ：用注意力权重对值 V V V 进行加权和。

3.2.4、对比与总结

上述公式本质上是描述了不同的注意力机制变种：

第一个公式采用线性变换和点积注意力的组合。
第二个公式使用线性变换和加性注意力的组合，其中加入了tanh激活函数。
第三个公式是标准的缩放点积注意力。

这些公式通过不同的方式计算查询和键之间的相似性，并利用这些相似性来加权输入的值 V V V，从而实现不同的注意力机制。在具体应用中，选择哪种机制往往取决于任务的需求和数据的特点。

3.2.5、bmm运算

说明：当注意力权重矩阵和V都是三维张量且第一维代表为batch条数时, 则做bmm运算.bmm是一种特殊的张量乘法运算.
如果参数1形状是(b × n × m), 参数2形状是(b × m × p), 则输出为(b × n × p)

4、注意力机制的作用

在 解码器端 的注意力机制：能够根据 模型目标 有效的聚焦编码器的输出结果，当其作为解码器的输入时提升效果，改善以往编码器输出是单一定长张量，无法存储过多信息的情况；

在 编码器端 的注意力机制：主要解决表征问题，相当于特征提取过程，得到输入的注意力表示

一般使用自注意力(self-attention)

注意力机制在网络中实现的图形表示：

5、注意力机制原理⭐

5.1、注意力机制示意图

Attention机制的工作原理并不复杂，我们可以用下面这张图做一个总结

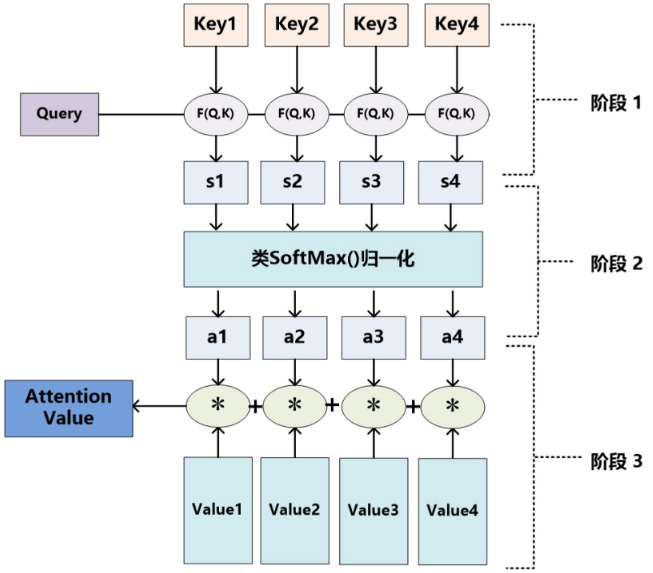
5.2、Attention计算过程

query 和 key 进行相似度计算，得到一个query 和 key 相关性的分值
将这个分值进行归一化(softmax)，得到一个注意力的分布
使用注意力分布和 value 进行计算，得到一个融合注意力的更好的 value 值

为了更好的说明上面的情况，我们通过注意力来做一个机器翻译(NMT) 的任务，机器翻译中，我们会使用 seq2seq 的架构，每个时间步从词典里生成一个翻译的结果。
就像下面这张图一样：

在没有注意力之前，我们每次都是根据 Encoder 部分的输出结果来进行生成，提出注意力后，就是想在生成翻译结果时并不是看 Encoder 中所有的输出结果，而是先来看看想生成的这部分和哪些单词可能关系会比较大，关系大的我多借鉴些；关系小的，少借鉴些。

就是这样一个想法，我们看看该如何操作：

这里为了生成单词，我们把 Decoder 部分输入后得到的向量作为 query；把 Encoder 部分每个单词的向量作为 key；
首先我们先把 query 和每一个单词进行点乘score=query⋅keyscore=query⋅key，得到相关性的分值；
有了这些分值后，我们对这些分值做一个softmaxsoftmax ，得到一个注意力的分布；
有了这个注意力，我们就可以用它和 Encoder 的输出值 (value) 进行相乘，得到一个加权求和后的值；
这个值就包含注意力的表示，我们用它来预测要生成的词。

5.3、Attention计算逻辑

当然，Attention 并不是只有这一种计算方式，后来还有很多人找到了各种各样的计算注意力的方法；

比如我们上面介绍的三种计算规则，但是从本质上，它们都遵循着这个三步走的逻辑：

query 和 key 进行相似度计算，得到一个query 和 key 相关性的分值
将这个分值进行归一化(softmax)，得到一个注意力的分布
使用注意力分布和 value 进行计算，得到一个融合注意力的更好的 value 值

5.4、有无attention模型对比🔺

5.4.1、无attention机制的模型

RNN模型建立起了网络隐层之间的时序关联：

两个RNN组合，即为Encoder-Decoder模型：

工作机制如下：

文本处理领域的Encoder-Decoder框架可以这么直观地去理解 ：可以把它看作适合处理由一个句子（或篇章）生成另外一个句子（或篇章）的通用处理模型。

对于句子对 ，我们的目标是给定输入句子Source，期待通过Encoder-Decoder框架来生成目标句子Target。

Source和Target可以是同一种语言，也可以是两种不同的语言。

而Source和Target分别由各自的单词序列构成：
S o u r c e = ⟨ X 1 , X 2 ⋯ X m ⟩ Source = \langle X_1, X_2 \cdots X_m \rangle Source=⟨X1,X2⋯Xm⟩
T a r g e t = ⟨ y 1 , y 2 ⋯ y n ⟩ Target = \langle y_1, y_2 \cdots y_n \rangle Target=⟨y1,y2⋯yn⟩

encoder顾名思义就是对输入句子Source进行编码，将输入句子通过非线性变换转化为中间语义表示 C C C，
C = F ( X 1 , X 2 ⋯ X m ) C = F(X_1, X_2 \cdots X_m) C=F(X1,X2⋯Xm)

对于解码器Decoder来说，其任务是根据句子 S o u r c e Source Source的中间语义表示 C C C和之前已经生成的历史信息 y 1 , y 2 , ⋯ y i − 1 y_1, y_2, \cdots y_{i-1} y1,y2,⋯yi−1来生成期待得到的单词 y i y_i yi： y i = G ( C , y 1 , y 2 ⋯ y i − 1 ) y_i = G(C, y_1, y_2 \cdots y_{i-1}) yi=G(C,y1,y2⋯yi−1)

上述图中展示的Encoder-Decoder框架是没有体现出"注意力模型"的，

所以可以把它看作是 注意力未集中 的模型

为什么说它注意力不集中呢？请观察下目标句子Target中每个单词的生成过程如下：
y 1 = f ( C ) y_1 = f(C) y1=f(C)
y 2 = f ( C , y 1 ) y_2 = f(C, y_1) y2=f(C,y1)
y 3 = f ( C , y 1 , y 2 ) y_3 = f(C, y_1, y_2) y3=f(C,y1,y2)

其中 f f f是Decoder的非线性变换函数。

从这里可以看出，在生成目标句子的单词时，不论生成哪个单词，它们使用的输入句子Source的语义编码 C C C都是一样的，没有任何区别 。

每个 y i y_i yi都依次这么产生，那么看起来就是整个系统根据输入句子Source生成了目标句子Target

如果Source是中文句子，Target是英文句子，那么这就是解决 机器翻译问题的Encoder-Decoder框架 ；

如果Source是一篇文章，Target是概括性的几句描述语句，那么这是 文本摘要的Encoder-Decoder框架 ；

如果Source是一句问句，Target是一句回答，那么这是问答系统或者 对话机器人的Encoder-Decoder框架。

由此可见，在文本处理领域，Encoder-Decoder的应用领域相当广泛

问题点是：语义编码 C C C是由句子Source的每个单词经过Encoder 编码产生的，这意味着不论是生成哪个单词，其实句子Source中任意单词对生成某个目标单词 y i y_i yi来说影响力都是相同的，这是为何说这个模型没有体现出注意力的缘由。这类似于人类看到眼前的画面，但是眼中却没有注意焦点一样.

5.4.2、有attention机制的模型

如果拿机器翻译来解释这个分心模型的Encoder-Decoder框架更好理解，比如输入的是英文句子"Tom chase Jerry"，Encoder-Decoder框架逐步生成中文单词："汤姆"，"追逐"，"杰瑞"；
在翻译"杰瑞"这个中文单词的时候，分心模型里面的每个英文单词对于翻译目标单词"杰瑞"贡献是相同的，很明显这里不太合理，显然"Jerry"对于翻译成"杰瑞"更重要，但是分心模型是无法体现这一点的，这就是为何说它没有引入注意力的原因。
没有引入注意力的模型在输入句子比较短的时候问题不大，但是如果输入句子比较长，此时所有语义完全通过一个中间语义向量来表示，单词自身的信息已经消失，可想而知会丢失很多细节信息，这也是为何要引入注意力模型的重要原因。

上面的例子中，如果引入Attention模型的话，应该在翻译"杰瑞"的时候，体现出英文单词对于翻译当前中文单词不同的影响程度，比如给出类似下面一个概率分布值：（Tom,0.3）(Chase,0.2) (Jerry,0.5)；

每个英文单词的概率代表了翻译当前单词"杰瑞"时，注意力分配模型分配给不同英文单词的注意力大小。

这对于正确翻译目标语单词肯定是有帮助的，因为引入了新的信息。

同理，目标句子中的每个单词都应该学会其对应的源语句子中单词的注意力分配概率信息。

这意味着在生成每个单词的时候，原先都是相同的中间语义表示 C C C会被替换成根据当前生成单词而不断变化的。

理解Attention模型的关键就是这里，即由固定的中间语义表示 C C C换成了根据当前输出单词来调整成加入注意力模型的变化的。

增加了注意力模型的Encoder-Decoder框架理解起来如下图所示：

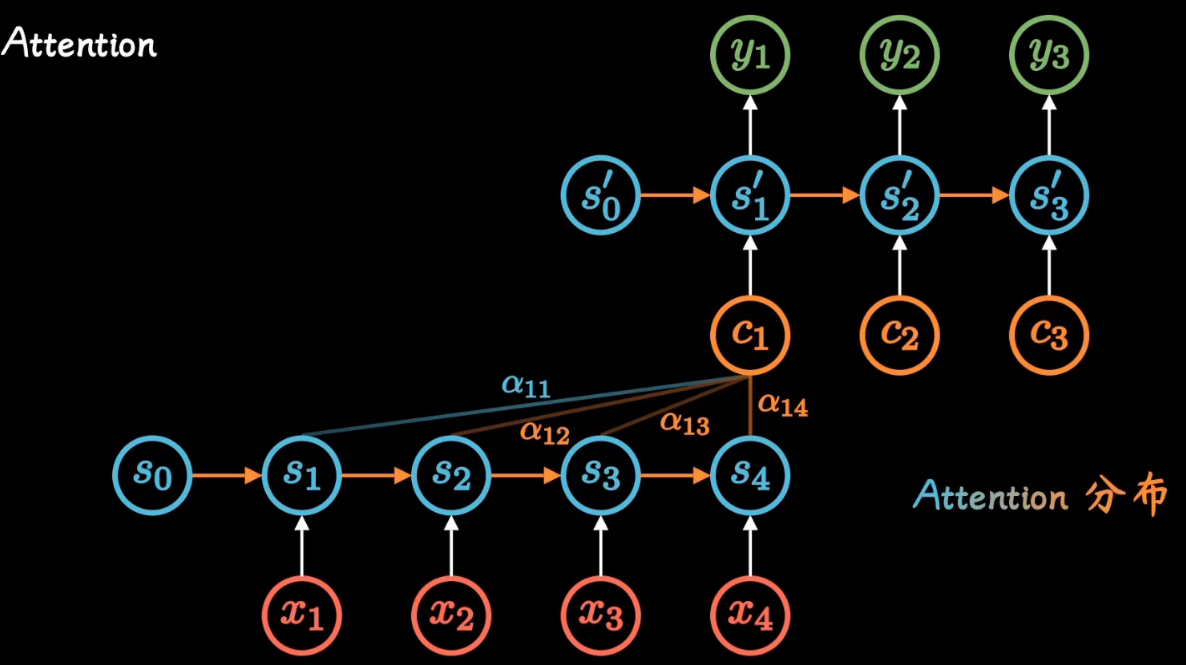
每个时间输入不同的 C C C

由于RNN并行运算效率太低，而Attention又对每一步进行了source打分，那么简化一下，就是self-attention。

多次重复，得到更佳结果：

回到简单的引入Attention机制的Encoder-Decoder模型：

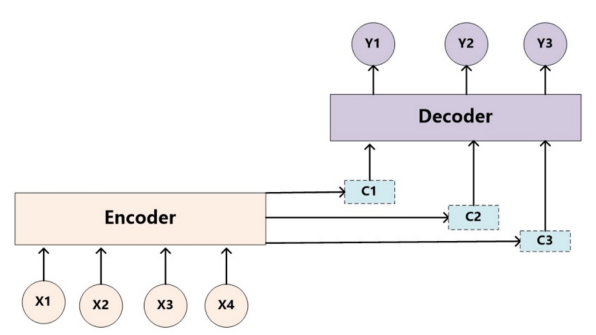
即生成目标句子单词的过程成了下面的形式：
y 1 = f 1 ( C 1 ) y_1 = f1(C_1) y1=f1(C1)
y 2 = f 1 ( C 2 , y 1 ) y_2 = f1(C_2, y_1) y2=f1(C2,y1)
y 3 = f 1 ( C 3 , y 1 , y 2 ) y_3 = f1(C_3, y_1, y_2) y3=f1(C3,y1,y2)

而每个 C i C_i Ci可能对应着不同的源句子单词的注意力分配概率分析，比如对于上面的英语翻译来说，其对应的信息可能如下：
C T o m = g ( 0.6 ∗ f 2 ( T o m ) , 0.2 ∗ f 2 ( C h a s e ) , 0.2 ∗ f 2 ( J e r r y ) ) C_{Tom} = g(0.6 * f_2(Tom), 0.2 * f_2(Chase), 0.2 * f_2(Jerry)) CTom=g(0.6∗f2(Tom),0.2∗f2(Chase),0.2∗f2(Jerry)) C C h a s e = g ( 0.2 ∗ f 2 ( T o m ) , 0.7 ∗ f 2 ( C h a s e ) , 0.1 ∗ f 2 ( J e r r y ) ) C_{Chase} = g(0.2 * f_2(Tom), 0.7 * f_2(Chase), 0.1 * f_2(Jerry)) CChase=g(0.2∗f2(Tom),0.7∗f2(Chase),0.1∗f2(Jerry)) C J e r r y = g ( 0.3 ∗ f 2 ( T o m ) , 0.2 ∗ f 2 ( C h a s e ) , 0.5 ∗ f 2 ( J e r r y ) ) C_{Jerry} = g(0.3 * f_2(Tom), 0.2 * f_2(Chase), 0.5 * f_2(Jerry)) CJerry=g(0.3∗f2(Tom),0.2∗f2(Chase),0.5∗f2(Jerry))

f 2 f_2 f2函数代表Encoder对输入 A A A英文单词的 某种变换函数

比如，如果Encoder是用的RNN模型的话，这个 f 2 f_2 f2函数的结果往往是某个时刻输入后隐层节点的状态值；

g g g代表Encoder根据单词的中间表示 h h h 合成每个句子单词 C i C_i Ci表示的 变换函数，

一般的做法中， g g g函数就是对构成元素加权求和，即下列公式 C i = ∑ j = 1 L x a i j h j C_i = \sum_{j=1}^{L_x} a_{ij}h_j Ci=∑j=1Lxaijhj

L x L_x Lx代表输入句子source的长度；
a i j a_{ij} aij代表在Target输出第 i i i个单词时 source输入句子的第 j j j个单词的 注意力分配系数；

前面 C T o m C_{Tom} CTom就是Decoder输入句子中第一个单词 y 1 y_1 y1翻译'汤姆'时的 C 1 C_1 C1，

那么 L x = 3 L_x=3 Lx=3， h 1 = f 2 ( T o m ) , h 2 = f 2 ( C h a s e ) , h 3 = f 2 ( J e r r y ) h_1=f_2(Tom),h_2=f_2(Chase),h_3=f_2(Jerry) h1=f2(Tom),h2=f2(Chase),h3=f2(Jerry)分别输入句子每个单词的变换编码，对应的注意力模型权值分别为 0.6 , 0.2 , 0.2 0.6, 0.2, 0.2 0.6,0.2,0.2，所以 g g g函数 本质上就是加权求和函数 。

6、注意力机制实现步骤

6.1、步骤

根据注意力计算规则，对Q，K，V进行相应的计算
根据第一步采用的计算方法，如果是拼接方法，则需要将Q与第二步的计算结果再进行拼接；如果是转置点积，一般是自注意力；Q与V相同, 则不需要进行与Q的拼接
最后为了使整个Attention机制按照指定尺寸输出，使用线性层作用在第二步的结果上做一个线性变换，得到最终对Q的注意力表示

6.2、代码实现

常见注意力机制的代码：

python 复制代码

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/8/15 0:30
import torch  # 导入PyTorch库
import torch.nn as nn  # 导入PyTorch的神经网络模块
import torch.nn.functional as F  # 导入PyTorch的函数模块


class Attn(nn.Module):
    def __init__(self, query_size, key_size, value_size1, value_size2, output_size):
        """初始化函数中的参数有5个, query_size代表query的最后一维大小
           key_size代表key的最后一维大小, value_size1代表value的倒数第二维大小,
           value = (1, value_size1, value_size2)
           value_size2代表value的倒数第一维大小, output_size输出的最后一维大小"""
        super(Attn, self).__init__()  # 调用父类的初始化方法

        # 将以下参数传入类中
        self.query_size = query_size  # query的最后一维大小
        self.key_size = key_size  # key的最后一维大小
        self.value_size1 = value_size1  # value的倒数第二维大小
        self.value_size2 = value_size2  # value的倒数第一维大小
        self.output_size = output_size  # 输出的最后一维大小

        # 初始化注意力机制实现第一步中需要的线性层.
        self.attn = nn.Linear(self.query_size + self.key_size, value_size1)

        # 初始化注意力机制实现第三步中需要的线性层.
        self.attn_combine = nn.Linear(self.query_size + value_size2, output_size)

    def forward(self, Q, K, V):
        """forward函数的输入参数有三个, 分别是Q, K, V, 根据模型训练常识, 输入给Attention机制的
           张量一般情况都是三维张量, 因此这里也假设Q, K, V都是三维张量"""

        # 第一步, 按照计算规则进行计算,
        # 我们采用常见的第一种计算规则
        # 将Q，K进行纵轴拼接, 做一次线性变化, 最后使用softmax处理获得结果
        attn_weights = F.softmax(
            self.attn(torch.cat((Q[0], K[0]), 1)), dim=1)

        # 然后进行第一步的后半部分, 将得到的权重矩阵与V做矩阵乘法计算,
        # 当二者都是三维张量且第一维代表batch条数时, 则做bmm运算
        attn_applied = torch.bmm(attn_weights.unsqueeze(0), V)

        # 之后进行第二步, 通过取[0]是用来降维, 根据第一步采用的计算方法,
        # 需要将Q与第一步的计算结果再进行拼接
        output = torch.cat((Q[0], attn_applied[0]), 1)

        # 最后是第三步, 使用线性层作用在第三步的结果上做一个线性变换并扩展维度，得到输出
        # 因为要保证输出也是三维张量, 因此使用unsqueeze(0)扩展维度
        output = self.attn_combine(output).unsqueeze(0)

        return output, attn_weights


if __name__ == '__main__':
    query_size = 32  # 定义query的最后一维大小
    key_size = 32  # 定义key的最后一维大小
    value_size1 = 32  # 定义value的倒数第二维大小
    value_size2 = 64  # 定义value的倒数第一维大小
    output_size = 64  # 定义输出的最后一维大小
    attn = Attn(query_size, key_size, value_size1, value_size2, output_size)  # 初始化注意力机制模型

    # 生成随机的Q, K, V张量用于测试
    Q = torch.randn(1, 1, 32)  # 生成形状为(1, 1, 32)的随机张量Q
    K = torch.randn(1, 1, 32)  # 生成形状为(1, 1, 32)的随机张量K
    V = torch.randn(1, 32, 64)  # 生成形状为(1, 32, 64)的随机张量V

    # 调用注意力机制模型的forward函数
    out = attn(Q, K, V)
    print(out[0])  # 打印输出张量
    print(out[1])  # 打印注意力权重张量

输出效果:

E:\anaconda3\python.exe D:\Python\AI\自然语言处理\9-注意力机制.py
tensor([[[ 0.5189, -0.2593, -0.5739, -0.2848, 0.4385, 0.1746, -0.1233,
-0.1704, 0.1818, -0.1095, -0.2231, 0.2711, 0.2172, 0.3662,
0.0158, 0.3471, -0.3707, 0.0891, -0.2715, -0.1124, 0.0235,
-0.2087, 0.1196, -0.1750, -0.6529, 0.6124, -0.2354, -0.3289,
-0.2785, 0.2235, -0.0422, 0.2207, -0.3690, -0.3820, -0.3206,
-0.2428, -0.3565, -0.4306, 0.0448, -0.1710, 0.5619, -0.2440,
1.0866, 0.0629, -0.1259, 0.3751, 0.3944, -0.0861, 0.1009,
-0.1897, -0.1188, 0.1966, 0.0359, 0.1093, -0.3068, 0.4103,
0.0935, 0.4947, 0.2785, 0.3605, 0.1665, -0.1661, -0.5690,
0.0392]]], grad_fn=<UnsqueezeBackward0>)
tensor([[0.0140, 0.0424, 0.0132, 0.0285, 0.0503, 0.0429, 0.0255, 0.0216, 0.0376,
0.0287, 0.0218, 0.0429, 0.0217, 0.0182, 0.0299, 0.0089, 0.0481, 0.0251,
0.0209, 0.0198, 0.0654, 0.0380, 0.0291, 0.0229, 0.0468, 0.0715, 0.0350,
0.0192, 0.0162, 0.0258, 0.0402, 0.0279]], grad_fn=<SoftmaxBackward0>)

Process finished with exit code 0

从这部分代码，多少也能看出点东西，其实：Attention就是权重

6.3、代码流程图

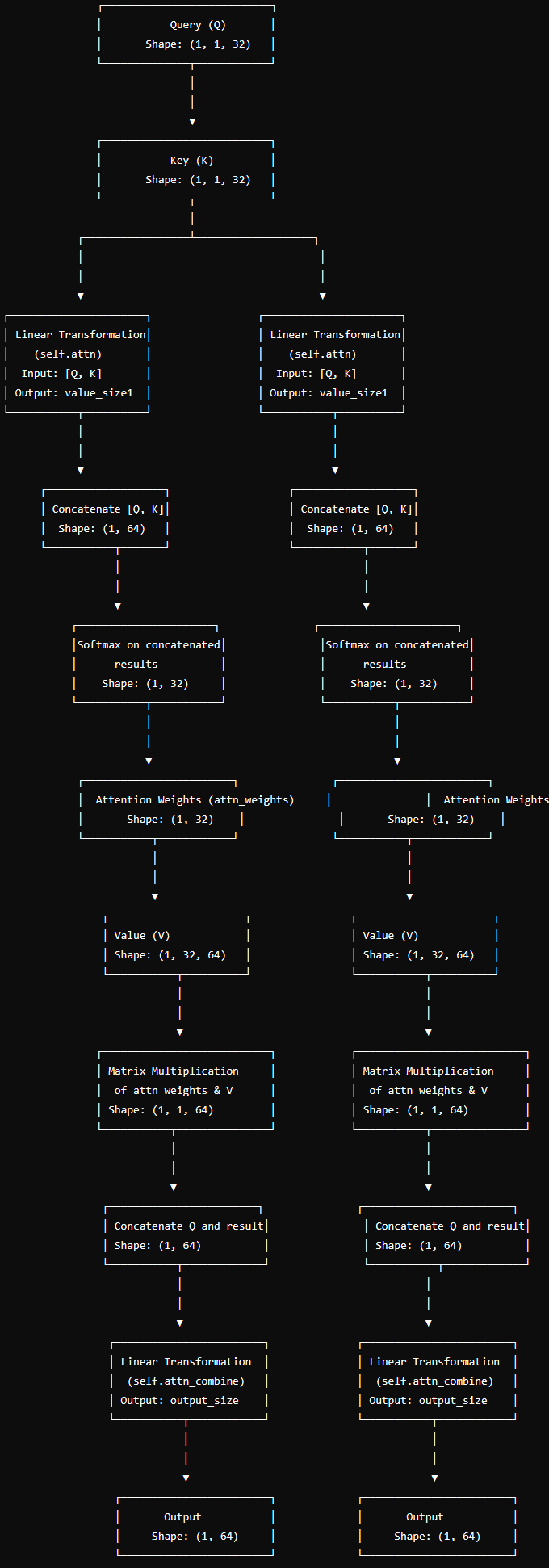
6.4、数学表达式

这段代码实现的是一种加性注意力（Additive Attention）的简化形式 具体数学表达式如下：

计算注意力得分（ s c o r e score score）： s c o r e = L i n e a r ( [ Q ; K ] ) score = Linear([\mathbf{Q}; \mathbf{K}]) score=Linear([Q;K])

其中 [ Q ; K ] [\mathbf{Q}; \mathbf{K}] [Q;K]表示 Q \mathbf{Q} Q和 K \mathbf{K} K的拼接

计算注意力权重（ w e i g h t s weights weights）： w e i g h t s = S o f t m a x ( s c o r e ) weights = Softmax(score) weights=Softmax(score)
计算上下文向量（ c o n t e x t v e c t o r context\ vector context vector）： c o n t e x t = w e i g h t s × V context = weights \times \mathbf{V} context=weights×V
拼接并线性变换： o u t p u t = L i n e a r ( [ Q ; c o n t e x t ] ) output = Linear([\mathbf{Q}; context]) output=Linear([Q;context])

7、小结

学习了什么是注意力计算规则：
1. 它需要三个指定的输入Q(query), K(key), V(value), 然后通过计算公式得到注意力的结果
2. 这个结果代表query在key和value作用下的注意力表示
3. 当输入的Q=K=V时, 称作自注意力计算规则
常见的注意力计算规则：
1. 将Q，K进行纵轴拼接, 做一次线性变化, 再使用softmax处理获得结果最后与V做张量乘法.
2. 将Q，K进行纵轴拼接, 做一次线性变化后再使用tanh函数激活, 然后再进行内部求和, 最后使用softmax处理获得结果再与V做张量乘法.
3. 将Q与K的转置做点积运算, 然后除以一个缩放系数, 再使用softmax处理获得结果最后与V做张量乘法.
学习了什么是注意力机制：
1. 注意力机制是注意力计算规则能够应用的深度学习网络的载体, 同时包括一些必要的全连接层以及相关张量处理, 使其与应用网络融为一体. 使自注意力计算规则的注意力机制称为自注意力机制.
注意力机制的作用：
1. 在解码器端的注意力机制：能够根据模型目标有效的聚焦编码器的输出结果, 当其作为解码器的输入时提升效果. 改善以往编码器输出是单一定长张量, 无法存储过多信息的情况.
2. 在编码器端的注意力机制：主要解决表征问题, 相当于特征提取过程, 得到输入的注意力表示. 一般使用自注意力(self-attention).
注意力机制原理：
1. query 和 key 进行相似度计算，得到一个query 和 key 相关性的分值
2. 将这个分值进行归一化(softmax)，得到一个注意力的分布
3. 使用注意力分布和 value 进行计算，得到一个融合注意力的更好的 value 值
注意力机制实现步骤：
1. 第一步：根据注意力计算规则, 对Q，K，V进行相应的计算.
2. 第二步：根据第一步采用的计算方法, 如果是拼接方法，则需要将Q与第二步的计算结果再进行拼接, 如果是转置点积, 一般是自注意力, Q与V相同, 则不需要进行与Q的拼接.
3. 第三步：最后为了使整个attention机制按照指定尺寸输出, 使用线性层作用在第二步的结果上做一个线性变换, 得到最终对Q的注意力表示.
学习并实现了一种常见的注意力机制的类Attn.