目录
引言
在 数据结构------栈 中我们学习了栈的相关知识,今天我们接着来学习数据结构------队列。
队列的定义
队列(Queue)是一种先进先出(FIFO, First-In-First-Out)的线性数据结构。它只允许在队列的一端(队尾)进行插入(enqueue)操作,而在另一端(队头)进行删除(dequeue)操作。这种操作方式确保了队列中元素的顺序性,即最先进入队列的元素将最先被移除。
如图所示:

队头(Front):队头是指队列中允许删除操作的一端。也就是说,队列中的元素将按照它们被添加到队列中的顺序,从队头开始被逐一移除。
队尾(Rear):队尾是指队列中允许插入操作的一端。新元素将被添加到队尾,以保持队列的先进先出(FIFO)特性。
队列的分类
队列与栈类似,同样可以用两种方式实现。分别是单链表和数组。接下来我们来分析一下如何使用两种方法实现队列。
1.单链表实现
我们可以将链表的头节点与尾节点分别作为队列的队首与队尾,这样我们就能用两个指针来对其进行操作。
如下图所示:

2.数组实现
问题一:
在使用数组实现队列时,可能会出现"假溢出"的情况。这是因为数组的头部和尾部是固定的,当队列的尾部达到数组的末尾时,即使数组的头部还有很多空闲空间,也无法再向队列中添加新元素。这种情况下,队列虽然看起来是满的,但实际上还有很多空间没有被利用。
解决方法:
我们可以将数组相接变成循环数组。
问题二:
变成循环数组又会出现新的问题:当队首与队尾下标都指向同一个节点 时,这个队列是空 还是满呢?
解决方法:
多使用一个空间便于我们区分队空和队满。若队列不为空,让队尾下标指向队尾的下一个位置。我们约定以队头指针在队尾指针的下一位置作为队满 的标志,即Queue->rear+1=Queue->front。
如下图所示:
队满状态:

队列的功能
1.队列的初始化。
2.判断队列是否为空。
3.判断队列是否已满。
4.返回队头元素。
5.返回队尾元素
6.返回队列的大小。
7.元素入队列。
8.元素出队列。
9.打印队列的元素。
10.销毁队列。
队列的声明
1.链式队列
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QDataType val;
}QNode;
typedef struct Queue
{
QNode* front;
QNode* rear;
int size;
}Queue;2.循环队列
typedef int QDataType;
#define MAXSIZE 30 //定义队列的最大值
typedef struct
{
QDataType* data;
int front; //头指针
int rear; //尾指针
}Queue;队列的功能实现
1.队列初始化
给队列中的各个元素给定值,以免出现随机值。
(1)链式队列
//初始化
void QueueInit(Queue* q)
{
assert(q);
q->front = NULL;
q->rear = NULL;
q->size = 0;
}(2)循环队列
//初始化
void QueueInit(Queue* q)
{
// 为队列的数据存储空间分配内存。
q->data = (QDataType*)malloc(sizeof(QDataType) * MAXSIZE);
if (q->data == NULL)
{
perror("malloc fail:");
return;
}
// 初始化队首和队尾指针为0,表示队列为空
q->front = q->rear = 0;
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列花费的是一个固定大小的空间,因此空间复杂度为O(1)。循环队列需要开辟整个队列的大小,因此空间复杂度为O(N)。
2.判断队列是否为空
(1)链式队列
判断size是否为0即可。
代码如下:
//判断队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);
return q->size == 0;
}(2)循环队列
判断front是否等于rear即可。
代码如下:
//判断队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);
return q->front == q->rear;
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
3.判断队列是否已满
(1)链式队列
链式队列不需要判断队列是否已满。
(2)循环队列
循环队列判断是否已满需要进行一些特殊处理。
代码如下:
//判断队列是否已满
bool QueueFull(Queue* q)
{
assert(q);
// 取模操作是避免越界
return q->front == (q->rear + 1) % MAXSIZE;
}(3)复杂度分析
时间复杂度:由于循环队列花费时间是一个常数,因此时间复杂度为O(1)。
空间复杂度:循环队列花费的是一个固定大小的空间,所以空间复杂度为O(1)。
4.返回队头元素
(1)链式队列
//读取队头数据
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->front);
return q->front->val;
}(2)循环队列
//读取队头数据
QDataType QueueFront(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->data[q->front];
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
5.返回队尾元素
(1)链式队列
//读取队尾数据
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->rear);
return q->rear->val;
}(2)循环队列
//读取队尾数据
QDataType QueueBack(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
// 当rear为0时,rear-1会导致负数索引,这在数组中是无效的
// 通过加上MAXSIZE并取模MAXSIZE,我们可以确保索引始终在有效范围内
// 这里(q->rear - 1 + MAXSIZE) % MAXSIZE计算的是队尾元素的索引
return q->data[(q->rear - 1 + MAXSIZE) % MAXSIZE];
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
6.返回队列大小
(1)链式队列
链式队列求队列大小很简单,直接返回size即可。
代码如下:
//统计队列数据个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}(2)循环队列
我们来分析一下:

像这个可以使用rear-front求出队列的大小。但是要知道,这是个循环队列,rear时=是可以跑到front之后的,如下图所示:
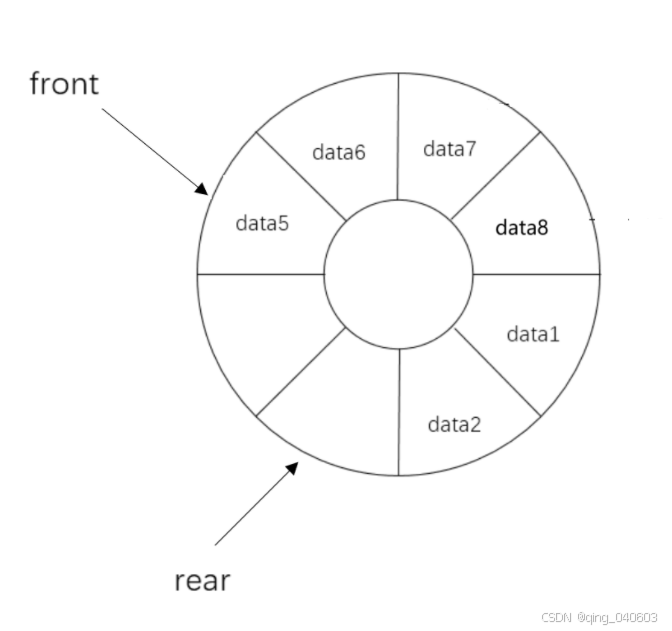
解决方法:rear减去front之后加个MAXSIZE就好了。
代码如下:
//统计队列数据个数
int QueueSize(Queue* q)
{
assert(q);
return (q->rear - q->front + MAXSIZE) % MAXSIZE;
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
7.元素入队列
(1)链式队列
链式队列元素入队需要判断队列是否为空的情况。
代码如下:
//队尾插入
void QueuePush(Queue* q, QDataType x)
{
assert(q);
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
perror("malloc fail");
return;
}
newNode->next = NULL;
newNode->val = x;
// 如果队列为空
if (q->rear == NULL)
{
// 新节点既是队首也是队尾
q->front = q->rear = newNode;
}
else
{
// 将当前队尾节点的next指向新节点
q->rear->next = newNode;
// 更新队尾指针为新节点
q->rear = newNode;
}
q->size++;
}(2)循环队列
取模操作不能少,确保不会越界。
//队尾插入
void QueuePush(Queue* q, QDataType x)
{
assert(q);
if (QueueFull)
{
printf("队列已满\n");
return;
}
q->data[q->rear] = x;
// rear指针向后移动
// (q->rear + 1) % MAXSIZE这段代码
// 确保了rear指针的值始终在0到MAXSIZE-1的范围内循环
q->rear = (q->rear + 1) % MAXSIZE;
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
8.元素出队列
(1)链式队列
//队头删除
void QueuePop(Queue* q)
{
assert(q);
assert(q->size != 0);
// 检查队列中是否只有一个节点
if (q->front->next == NULL)
{
free(q->front);
// 队列变为空,队首和队尾指针都设置为NULL
q->front = q->rear = NULL;
}
// 多个节点
else
{
// 保存下一个节点的指针
QNode* next = q->front->next;
// 释放队首节点
free(q->front);
// 更新队首指针为下一个节点
q->front = next;
}
q->size--;
}(2)循环队列
//队头删除
void QueuePop(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
// front指针向后移动
// (q->front + 1) % MAXSIZE这段代码
// 确保了front指针的值始终在0到MAXSIZE-1的范围内循环
q->front = (q->front + 1) % MAXSIZE;
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列花费时间都是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
9.打印队列元素
(1)链式队列
//打印队列元素
void QueuePrint(Queue* q)
{
assert(q);
QNode* cur = q->front;
QNode* tail = q->rear;
printf("队头->");
while (cur != tail->next)
{
printf("%d->", cur->val);
cur = cur->val;
}
printf("队尾\n");
}(2)循环队列
//打印队列元素
void QueuePrint(Queue* q)
{
assert(q);
int cur = q->front;
printf("队头->");
while (cur != q->rear)
{
printf("%d->", q->data[cur]);
// 避免越界
cur = (cur + 1) % MAXSIZE;
}
printf("队尾\n");
}(3)复杂度分析
时间复杂度:由于链式队列和循环队列都需要遍历整个队列,因此时间复杂度为O(n)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
10.销毁队列
(1)链式队列
//销毁
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
q->front = q->rear = NULL;
q->size = 0;
}(2)循环队列
//销毁
void QueueDestroy(Queue* q)
{
assert(q);
free(q->data);
q->data = NULL;
q->front = q->rear = 0;
}(3)复杂度分析
时间复杂度:由于链式队列需要遍历整个队列,因此时间复杂度为O(n)。循环队列花费时间是一个常数,因此时间复杂度为O(1)。
空间复杂度:由于链式队列和循环队列花费空间都是一个常数,因此空间复杂度为O(1)。
链式队列和循环队列的对比
|----------|------------------------------------|-----------------------------------------------|
| | 链式列表 | 循环列表 |
| 数据结构 | 使用链表实现,队列中的每个元素都是一个链表节点,节点之间通过指针相连 | 使用数组实现,但在逻辑上将数组的头尾相连,形成一个环形结构。 |
| 内存管理 | 出队或清空队列时需要释放链表节点的内存 | 无需手动释放内存,因为队列元素存储在数组中,数组的内存由系统自动管理 |
| 时间效率 | 由于使用头指针与尾指针,因此链式队的出队与入队的时间都相对较小 | 循环队列是基于数组实现的,支持下标的随机访问,所以时间消耗并不大 |
| 空间效率 | 空间使用灵活,可以根据需要动态地增加或减少内存分配 | 空间使用相对固定,需要预先定义最大容量。如果队列的实际大小远小于最大容量,则会造成空间浪费 |
完整代码
1.链式队列
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QDataType val;
}QNode;
typedef struct Queue
{
QNode* front;
QNode* rear;
int size;
}Queue;
//初始化
void QueueInit(Queue* q);
//销毁
void QueueDestroy(Queue* q);
//队尾插入
void QueuePush(Queue* q, QDataType x);
//队头删除
void QueuePop(Queue* q);
//读取队头数据
QDataType QueueFront(Queue* q);
//读取队尾数据
QDataType QueueBack(Queue* q);
//统计队列数据个数
int QueueSize(Queue* q);
//判断队列是否为空
bool QueueEmpty(Queue* q);
//打印队列元素
void QueuePrint(Queue* q);Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"
//初始化
void QueueInit(Queue* q)
{
assert(q);
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
//销毁
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
q->front = q->rear = NULL;
q->size = 0;
}
//队尾插入
void QueuePush(Queue* q, QDataType x)
{
assert(q);
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
perror("malloc fail");
return;
}
newNode->next = NULL;
newNode->val = x;
// 如果队列为空
if (q->rear == NULL)
{
// 新节点既是队首也是队尾
q->front = q->rear = newNode;
}
else
{
// 将当前队尾节点的next指向新节点
q->rear->next = newNode;
// 更新队尾指针为新节点
q->rear = newNode;
}
q->size++;
}
//队头删除
void QueuePop(Queue* q)
{
assert(q);
assert(q->size != 0);
// 检查队列中是否只有一个节点
if (q->front->next == NULL)
{
free(q->front);
// 队列变为空,队首和队尾指针都设置为NULL
q->front = q->rear = NULL;
}
// 多个节点
else
{
// 保存下一个节点的指针
QNode* next = q->front->next;
// 释放队首节点
free(q->front);
// 更新队首指针为下一个节点
q->front = next;
}
q->size--;
}
//读取队头数据
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->front);
return q->front->val;
}
//读取队尾数据
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->rear);
return q->rear->val;
}
//统计队列数据个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
//判断队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);
return q->size == 0;
}
//打印队列元素
void QueuePrint(Queue* q)
{
assert(q);
QNode* cur = q->front;
QNode* tail = q->rear;
printf("队头->");
while (cur != tail->next)
{
printf("%d->", cur->val);
cur = cur->val;
}
printf("队尾\n");
}2.循环队列
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int QDataType;
#define MAXSIZE 30
typedef struct
{
QDataType* data;
int front;
int rear;
}Queue;
//初始化
void QueueInit(Queue* q);
//销毁
void QueueDestroy(Queue* q);
//队尾插入
void QueuePush(Queue* q, QDataType x);
//队头删除
void QueuePop(Queue* q);
//读取队头数据
QDataType QueueFront(Queue* q);
//读取队尾数据
QDataType QueueBack(Queue* q);
//统计队列数据个数
int QueueSize(Queue* q);
//判断队列是否为空
bool QueueEmpty(Queue* q);
//打印队列元素
void QueuePrint(Queue* q);
//判断队列是否已满
bool QueueFull(Queue* q);Queue.h
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"
//初始化
void QueueInit(Queue* q)
{
// 为队列的数据存储空间分配内存。
q->data = (QDataType*)malloc(sizeof(QDataType) * MAXSIZE);
if (q->data == NULL)
{
perror("malloc fail:");
return;
}
// 初始化队首和队尾指针为0,表示队列为空
q->front = q->rear = 0;
}
//销毁
void QueueDestroy(Queue* q)
{
assert(q);
free(q->data);
q->data = NULL;
q->front = q->rear = 0;
}
//队尾插入
void QueuePush(Queue* q, QDataType x)
{
assert(q);
if (QueueFull(q))
{
printf("队列已满\n");
return;
}
q->data[q->rear] = x;
// rear指针向后移动
// (q->rear + 1) % MAXSIZE这段代码
// 确保了rear指针的值始终在0到MAXSIZE-1的范围内循环
q->rear = (q->rear + 1) % MAXSIZE;
}
//队头删除
void QueuePop(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
// front指针向后移动
// (q->front + 1) % MAXSIZE这段代码
// 确保了front指针的值始终在0到MAXSIZE-1的范围内循环
q->front = (q->front + 1) % MAXSIZE;
}
//读取队头数据
QDataType QueueFront(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->data[q->front];
}
//读取队尾数据
QDataType QueueBack(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));
// 当rear为0时,rear-1会导致负数索引,这在数组中是无效的
// 通过加上MAXSIZE并取模MAXSIZE,我们可以确保索引始终在有效范围内
// 这里(q->rear - 1 + MAXSIZE) % MAXSIZE计算的是队尾元素的索引
return q->data[(q->rear - 1 + MAXSIZE) % MAXSIZE];
}
//统计队列数据个数
int QueueSize(Queue* q)
{
assert(q);
return (q->rear - q->front + MAXSIZE) % MAXSIZE;
}
//判断队列是否为空
bool QueueEmpty(Queue* q)
{
assert(q);
return q->front == q->rear;
}
//判断队列是否已满
bool QueueFull(Queue* q)
{
assert(q);
return q->front == (q->rear + 1) % MAXSIZE;
}
//打印队列元素
void QueuePrint(Queue* q)
{
assert(q);
int cur = q->front;
printf("队头->");
while (cur != q->rear)
{
printf("%d->", q->data[cur]);
// 避免越界
cur = (cur + 1) % MAXSIZE;
}
printf("队尾\n");
}结束语
本篇博客大致介绍了数据结构------队列的内容。
感谢每位能点进来阅读的大佬们!!!
十分感谢!!!
求点赞收藏关注!!!