目录
- [一、LeetCode 150. 逆波兰表达式求值](#一、LeetCode 150. 逆波兰表达式求值)
- [二、LeetCode 239. 滑动窗口最大值](#二、LeetCode 239. 滑动窗口最大值)
- [三、LeetCode 347.前 K 个高频元素](#三、LeetCode 347.前 K 个高频元素)
- 总结
一、LeetCode 150. 逆波兰表达式求值
题目链接: LeetCode 150. 逆波兰表达式求值
文章讲解:代码随想录
思路:
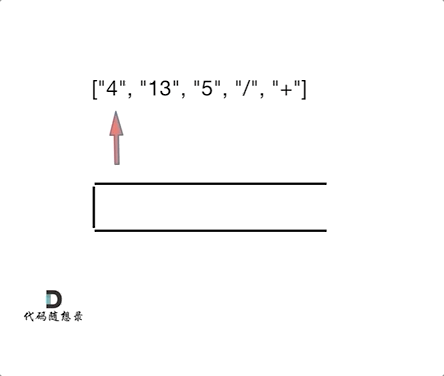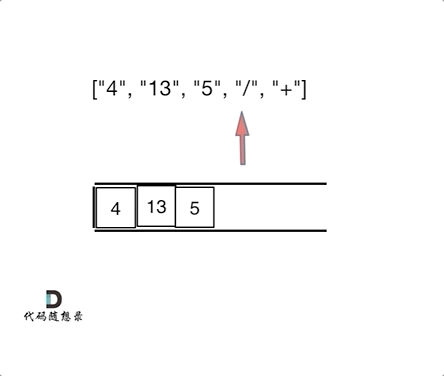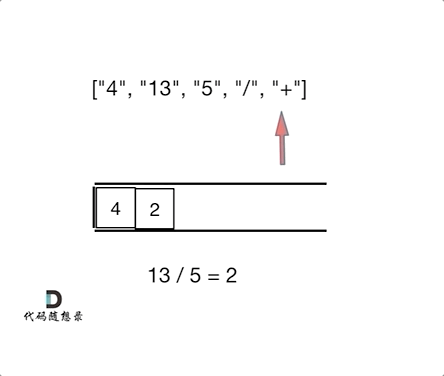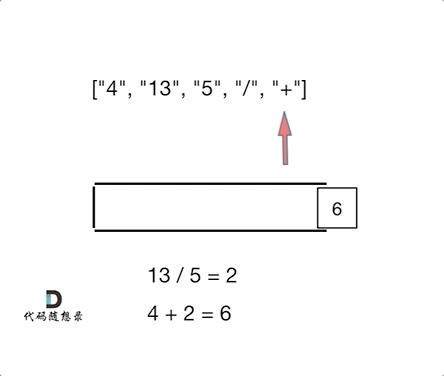
本题要求逆波兰表达式(后缀表达式)的值,后缀表达式实际上是一棵运算二叉树的后序遍历序列,中间结点为运算符,左右孩子为运算数字。由于后序遍历可以借助递归来实现,那么同样的,我们借助栈也能实现对这棵表达式二叉树的遍历运算。
具体算法思路为:当遍历到数字时,数字入栈;遍历到运算符时,将栈中最上面两个元素出栈,分别作为目标操作数( D S T DST DST)和源操作数( S R C SRC SRC),使用运算符运算后,将结果存在SRC中,运算结果入栈。表达式遍历结束后,栈中剩余的元素就是运算结果。
C++代码
cpp
class Solution {
public:
int evalRPN(vector<string>& tokens) {
long long src, dst;
stack<long long> nums;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" ||
tokens[i] == "/") {
dst = nums.top();
nums.pop();
src = nums.top();
nums.pop();
if (tokens[i][0] == '+') {
src += dst;
} else if (tokens[i][0] == '-') {
src -= dst;
} else if (tokens[i][0] == '*') {
src *= dst;
} else if (tokens[i][0] == '/') {
src /= dst;
}
} else {
src = stoll(tokens[i]);
}
nums.push(src);
}
int result = nums.top();
nums.pop();
return result;
}
};二、LeetCode 239. 滑动窗口最大值
题目链接: 添加链接描述
文章讲解:代码随想录
思路
本题可以自行构建一个单调队列进行解决。
单调队列,即队列中的元素按照一定顺序排列的数据结构。由于我们本题需要找出滑动窗口最大元素,因此我们可以自己构建一个降序的单调队列,队头为最大元素。单调队列设置一个自我维护的机制,即元素大于前面元素的时候,弹出前面元素,新元素入队尾,可以保证队列中的元素一定是降序排列的。
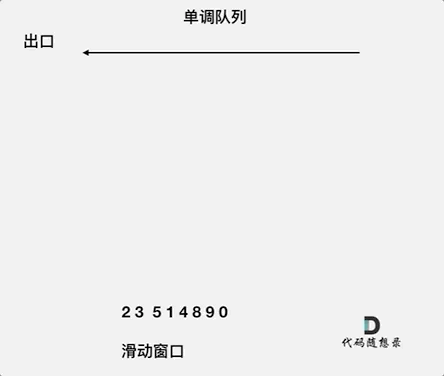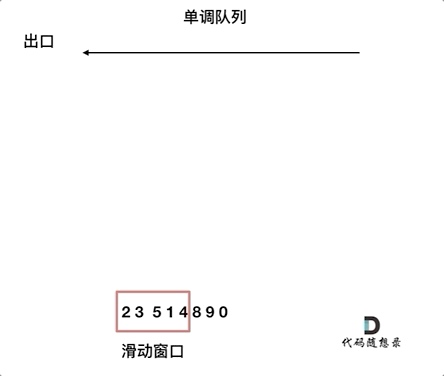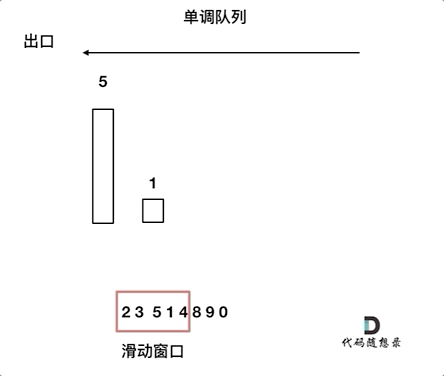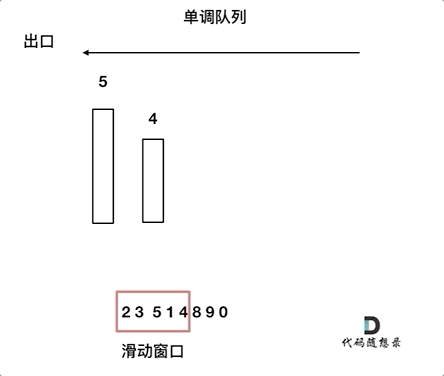
C++代码
cpp
class Solution {
private:
class MonoQue{ //构建单调队列,队列头部即为滑动窗口最大值
public:
deque<int> queue;
void push(int value){
while(!queue.empty() && value > queue.back()){
//大于号确保了不存在重复元素
queue.pop_back(); //从尾部入队,如果前面的元素小则弹出
}
queue.push_back(value);
}
void pop(int value){
if(value == queue.front()){ //队列中没有重复元素,可以直接判断相等
queue.pop_front();
}
}
};
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> output;
MonoQue que;
for(int i = 0; i < k; i++){ //第一个窗口中的元素入队
que.push(nums[i]);
}
output.push_back(que.queue.front());
for(int i = k; i < nums.size(); i++){
que.pop(nums[i-k]);
que.push(nums[i]);
output.push_back(que.queue.front());
}
return output;
}
};三、LeetCode 347.前 K 个高频元素
题目链接: LeetCode 347.前 K 个高频元素
文章讲解:代码随想录
思路
需要返回出现频率最高的前几个元素,首先我们需要统计各个元素出现次数,这里使用一种哈希结构unordered_map来实现统计;
统计结束后,需要对元素按照出现频率进行排序。我们选择构建一个优先级队列(小顶堆)
cpp
priority_queue<pair<int,int>, vector<pair<int,int>>, comparison> pri_que;其中尖括号内第一项是数据类型,第二项是实现该结构的底层容器,第三项是维护优先级队列的比较函数。
构建优先队列实现小顶堆,使堆中元素保持在3个,这样可以保证每次弹出的都是频率最小的元素,最后留在堆中的就是出现频率最大的元素。
C++代码
cpp
class Solution {
public:
class comparison{
public:
bool operator()(const pair<int,int> &l, const pair<int,int> &r){ //定义小顶堆比较函数
return l.second > r.second;
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int,int> freq_map;
for(int x: nums){ //map统计出现频率
freq_map[x]++;
}
priority_queue<pair<int,int>, vector<pair<int,int>>, comparison> pri_que;
//分别定义优先队列数据类型、底层容器与比较函数
for(auto it = freq_map.begin(); it != freq_map.end(); it++){
pri_que.push(*it);
if(pri_que.size() > k){ //保证固定大小k
pri_que.pop(); //小顶堆优先弹出最小值,因此后续可直接输出堆中k个值
}
}
vector<int> result;
while(!pri_que.empty()){
result.push_back(pri_que.top().first);
pri_que.pop();
}
return result;
}
};总结
接触到了单调队列和优先级队列两个新工具,对于滑动窗口最大值和前k个高频元素的代码思想应再进行复习理解。
文章图片来源:代码随想录 (https://programmercarl.com/)