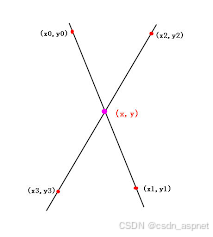
示例图
给定对应于线 AB 的点 A 和 B 以及对应于线 PQ 的点 P 和 Q,找到这些线的交点。这些点在 2D 平面中给出,并带有其 X 和 Y 坐标。示例:
输入:A = (1, 1), B = (4, 4)
C = (1, 8), D = (2, 4)
输出:给定直线 AB 和 CD 的交点
是:(2.4, 2.4)
输入:A = (0, 1), B = (0, 4)
C = (1, 8), D = (1, 4)
输出:给定直线 AB 和 CD 平行。
首先,假设我们有两个点 (x 1 , y 1 ) 和 (x 2 , y 2 )。现在,我们找到由这些点形成的直线方程。假设给定的直线为:
- a1x + b1y = c1
- a2x + b2y = c2
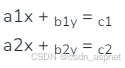
现在我们必须解这两个方程来找到交点。 为了求解,我们将 1 乘以 b 2并将 2 乘以 b 1这样我们得到 a 1 b 2 x + b 1 b 2 y = c 1 b 2 a 2 b 1 x + b 2 b 1 y = c 2 b 1减去这些我们得到 (a 1 b 2 -- a 2 b 1 ) x = c 1 b 2 -- c 2 b 1这样我们得到了 x 的值。 类似地,我们可以找到 y 的值。 (x, y) 给出了交点。**注意:**这给出了两条线的交点,但如果我们给出的是线段而不是直线,我们还必须重新检查这样计算出的点是否实际上位于两条线段上。如果线段由点 (x 1 , y 1 ) 和 (x 2 , y 2 ) 指定,那么要检查 (x, y) 是否在线段上,我们只需检查
- 最小值 (x 1 , x 2 ) <= x <= 最大值 (x 1 , x 2 )
- 最小值 (y 1 , y 2 ) <= y <= 最大值 (y 1 , y 2 )
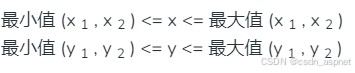
上述实现的伪代码:
determinant = a1 b2 - a2 b1
if (determinant == 0)
{
// Lines are parallel
}
else
{
x = (c1b2 - c2b1)/determinant
y = (a1c2 - a2c1)/determinant
}这些可以通过首先直接获得斜率,然后找到直线的截距来推导出来。
// C++ Implementation. To find the point of
// intersection of two lines
#include <bits/stdc++.h>
using namespace std;
// This pair is used to store the X and Y
// coordinates of a point respectively
#define pdd pair<double, double>
// Function used to display X and Y coordinates
// of a point
void displayPoint(pdd P)
{
cout << "(" << P.first << ", " << P.second
<< ")" << endl;
}
pdd lineLineIntersection(pdd A, pdd B, pdd C, pdd D)
{
// Line AB represented as a1x + b1y = c1
double a1 = B.second - A.second;
double b1 = A.first - B.first;
double c1 = a1*(A.first) + b1*(A.second);
// Line CD represented as a2x + b2y = c2
double a2 = D.second - C.second;
double b2 = C.first - D.first;
double c2 = a2*(C.first)+ b2*(C.second);
double determinant = a1*b2 - a2*b1;
if (determinant == 0)
{
// The lines are parallel. This is simplified
// by returning a pair of FLT_MAX
return make_pair(FLT_MAX, FLT_MAX);
}
else
{
double x = (b2*c1 - b1*c2)/determinant;
double y = (a1*c2 - a2*c1)/determinant;
return make_pair(x, y);
}
}
// Driver code
int main()
{
pdd A = make_pair(1, 1);
pdd B = make_pair(4, 4);
pdd C = make_pair(1, 8);
pdd D = make_pair(2, 4);
pdd intersection = lineLineIntersection(A, B, C, D);
if (intersection.first == FLT_MAX &&
intersection.second==FLT_MAX)
{
cout << "The given lines AB and CD are parallel.\n";
}
else
{
// NOTE: Further check can be applied in case
// of line segments. Here, we have considered AB
// and CD as lines
cout << "The intersection of the given lines AB "
"and CD is: ";
displayPoint(intersection);
}
return 0;
}
输出:
给定直线 AB 和 CD 的交点为:(2.4,2.4)
时间复杂度: O(1)
辅助空间: O(1)