通过探索看似不相关的大语言模型(LLM)架构之间的潜在联系,我们可能为促进不同模型间的思想交流和提高整体效率开辟新的途径。
尽管Mamba等线性循环神经网络(RNN)和状态空间模型(SSM)近来备受关注,Transformer架构仍然是LLM的主要支柱。这种格局可能即将发生变化:像Jamba、Samba和Griffin这样的混合架构展现出了巨大的潜力。这些模型在时间和内存效率方面明显优于Transformer,同时在能力上与基于注意力的LLM相比并未显著下降。
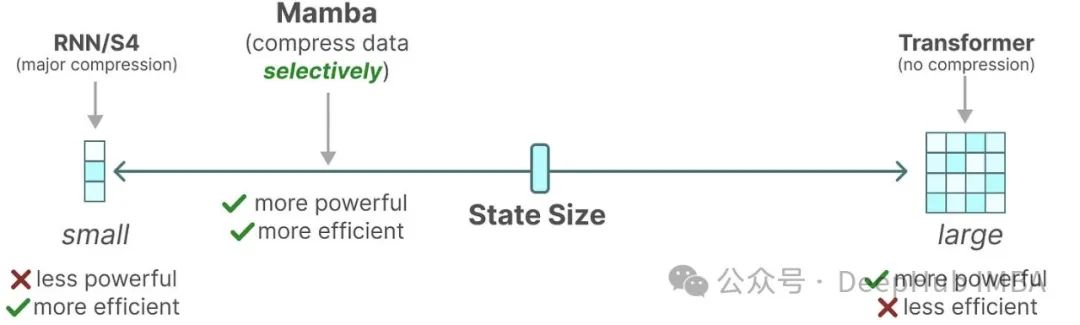
近期研究揭示了不同架构选择之间的深层联系,包括Transformer、RNN、SSM和matrix mixers,这一发现具有重要意义,因为它为不同架构间的思想迁移提供了可能。本文将深入探讨Transformer、RNN和Mamba 2,通过详细的代数分析来理解以下几点:
- Transformer在某些情况下可以视为RNN(第2节)
- 状态空间模型可能隐藏在自注意力机制的掩码中(第4节)
- Mamba在特定条件下可以重写为掩码自注意力(第5节)
这些联系不仅有趣,还可能对未来的模型设计产生深远影响。
LLM中的掩码自注意力机制
首先,让我们回顾一下经典的LLM自注意力层的结构:
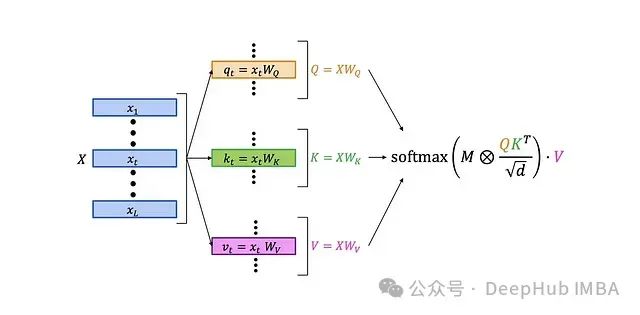
更详细的结构如下:
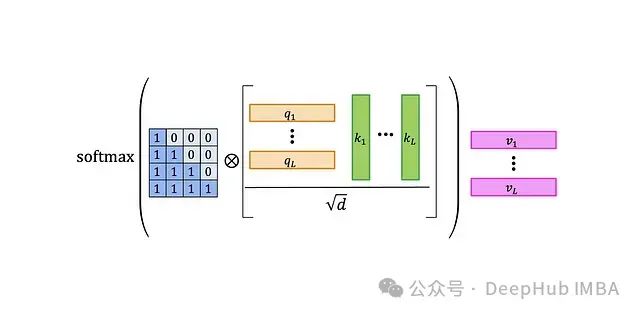
自注意力层的工作流程如下:
- 将查询矩阵Q和键矩阵K相乘,得到一个L×L的矩阵,包含查询和键的标量积。
- 对结果矩阵进行归一化。
- 将归一化后的矩阵与L×L的注意力掩码进行元素级乘法。图中展示了默认的因果掩码------左侧的0-1矩阵。这一步骤将较早查询与较晚键的乘积置零,防止注意力机制"看到未来"。
- 对结果应用softmax函数。
- 最后,将注意力权重矩阵A与值矩阵V相乘。输出的第t行可表示为:
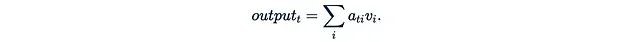
这意味着第i个值是通过"第t个查询对第i个键的注意力权重"来加权的。
这种架构中的多个设计选择都可能被修改。接下来我们将探讨一些可能的变体。
线性化注意力
注意力公式中的Softmax函数确保了值是以和为1的正系数混合的。这种设计保持了某些统计特性,但同时也带来了限制。例如即使我们希望利用结合律,如(QK^T)V = Q(K^TV),也无法突破Softmax的限制。
为什么结合律如此重要?因为改变乘法顺序可能显著影响计算复杂度:
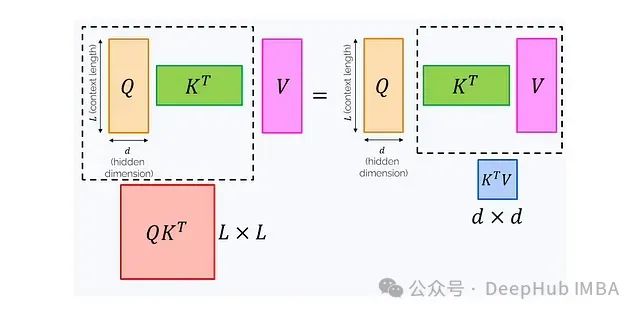
左侧公式需要计算一个L×L矩阵,如果这个矩阵完全显现在内存中,复杂度为O(L²d),内存消耗为O(L²)。右侧公式需要计算一个d×d矩阵,复杂度为O(Ld²),内存消耗为O(d²)。
随着上下文长度L的增加,左侧公式的计算成本rapidly become prohibitively非常的高。为了解决这个问题,我们可以考虑移除Softmax。详细展开带有Softmax的公式:

其中
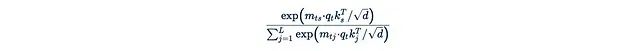
是Softmax函数。指数函数是主要的障碍,它阻止了我们从中提取任何项。如果我们直接移除指数函数:
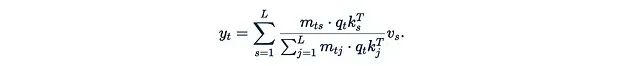
那么归一化因子
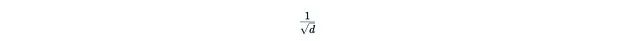
也随之消失。
这个简化后的公式存在一个问题:q_t^T k_s不能保证为正,这可能导致值以不同符号的系数混合,这在理论上是不合理的。更糟糕的是,分母可能为零,会导致计算崩溃。为了缓解这个问题,我们可以引入一个"良好的"元素级函数φ(称为核函数):

原始研究建议使用φ(x) = 1 + elu(x)作为核函数。
这种注意力机制的变体被称为线性化注意力。它的一个重要优势是允许我们利用结合律:
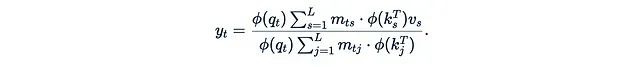
括号中M, K^T和V之间的关系现在变得相当复杂,不再仅仅是普通的矩阵乘法和元素级乘法。我们将在下一节详细讨论这个计算单元。
如果M是一个因果掩码,即对角线及以下为1,对角线以上为0:
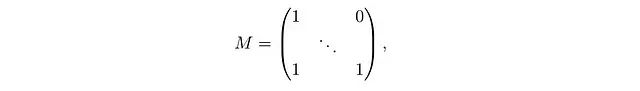
那么计算可以进一步简化:
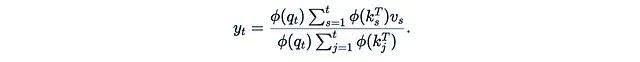
这可以通过一种简单的递归方式计算:
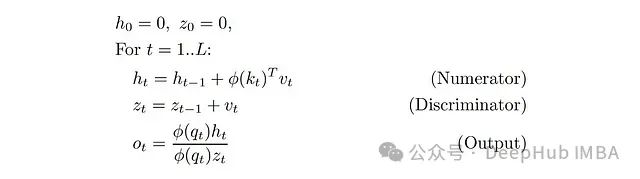
这是在2020年ICML上首次提出线性化注意力的论文"Transformers are RNNs"。在这个公式中,我们有两个隐藏状态:向量z_t和矩阵h_t(φ(k_t)^T v_t是列向量乘以行向量,得到一个d×d矩阵。
而近期的研究often以更简化的形式呈现线性化注意力,去除了φ函数和分母:
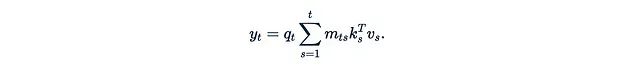
线性化注意力具有两个主要优势:
- 作为递归机制,它在推理时相对于序列长度L具有线性复杂度。
- 作为Transformer模型,它可以高效地并行训练。
但是你可能会问:如果线性化注意力如此优秀,为什么它没有在所有LLM中广泛应用?我们在讨论注意力的二次复杂度问题?实际上基于线性化注意力的LLM在训练过程中stability较低,且capability略逊于标准自注意力。这可能是因为固定的d×d形状的瓶颈比可调整的L×L形状的瓶颈能传递的信息更少。
进一步探索
RNN和线性化注意力之间的联系在近期的多项研究中得到了重新发现和深入探讨。一个common pattern是使用具有如下更新规则的矩阵隐藏状态:
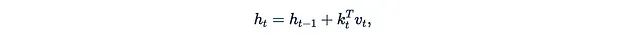
其中k_t和v_t可以视为某种"键"和"值",RNN层的输出形式为:
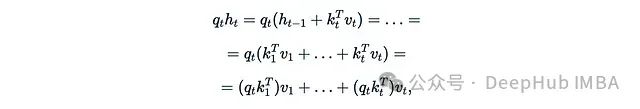
这本质上等同于线性注意力。下面两篇论文提供了有趣的一些样例:
1、xLSTM (2024年5月): 该论文提出了对著名的LSTM递归架构的改进。其mLSTM块包含一个矩阵隐藏状态,更新方式如下:
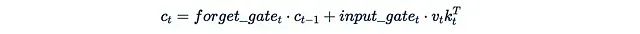
输出通过将这个状态与一个"查询"相乘得到。(注意:该论文的线性代数设置与我们的相反,查询、键和值是列向量而非行向量,因此v_t k_t^T的顺序看起来可能有些奇怪。)
2、Learning to (learn at test time) (2024年7月): 这是另一种具有矩阵隐藏状态的RNN架构,它的隐藏状态W是一个函数的参数,在t的迭代过程中通过梯度下降优化:
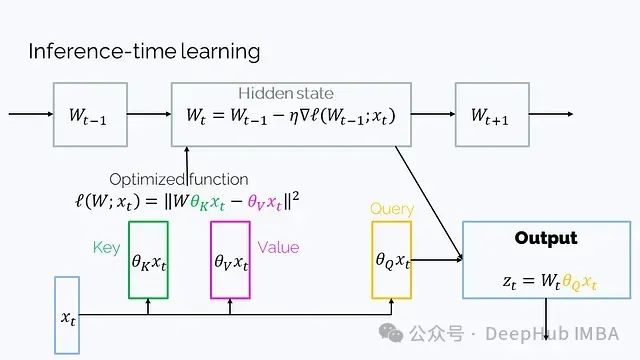
这里的设置也是转置的,因此顺序看起来有些不同。尽管数学表达比W_t = W_{t-1} + v_t k_t^T更复杂,但可以简化为这种形式。
以上两篇论文我们都详细介绍过,有兴趣的可以自行搜索
注意力掩码
在简化了掩码注意力机制后,我们可以开始探索其潜在的发展方向。一个明显的研究方向是选择不同的下三角矩阵(确保不会"看到未来")作为掩码M,而不是简单的0-1因果掩码。在进行这种探索之前,我们需要解决由此带来的效率问题。
在前一节中,我们使用了一个简单的0-1因果掩码M,这使得递归计算成为可能。但在一般情况下,这种递归技巧不再适用:
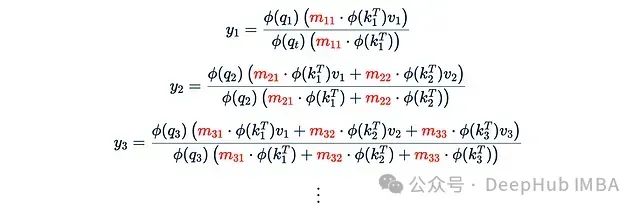
系数m_ts不再相同,也不存在将y_3与y_2关联的简单递归公式。因此,对于每个t我们都需要从头开始计算总和,这使得计算复杂度再次变为L的二次方而不是线性的。
解决这个问题的关键在于我们不能使用任意的掩码M,而应该选择特殊的、"良好"的掩码。我们需要那些可以快速与其他矩阵相乘(注意不是元素级乘法)的掩码。为了理解如何从这种特性中获益,让我们详细分析如何高效计算:
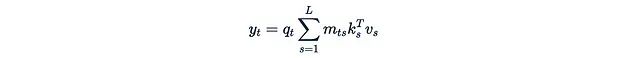
首先明确这个表达式的含义:
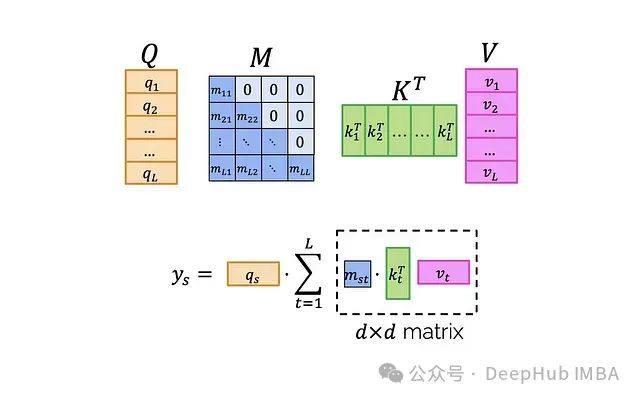
如果深入到单个索引级别:
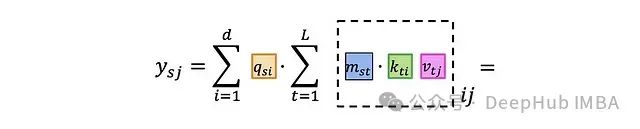
为了便于后续讨论,可以用不同的颜色标记索引,而不是块:
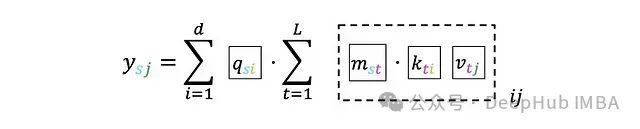
现在我们可以提出一个四步算法:
步骤1. 利用K和V创建一个三维张量Z,其中:

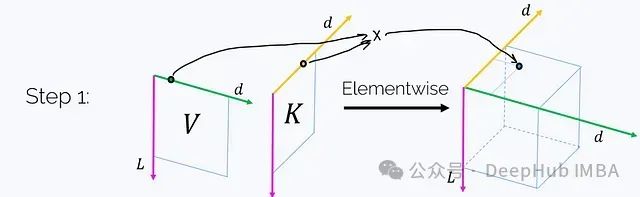
(每个轴都标注了其长度。)这一步骤需要O(Ld²)的时间和内存复杂度。值得注意的是,如果我们在洋红色轴t上对这个张量求和,我们将得到矩阵乘积K^T V:
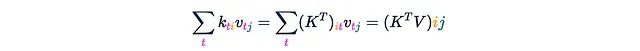
步骤2. 将M乘以这个张量(注意不是元素级乘法)。M乘以Z沿着洋红色轴t的每个"列"。
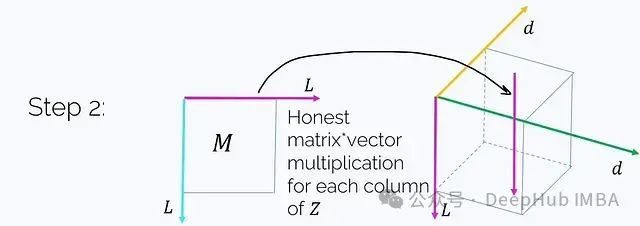
这正好得到:
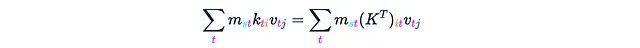
将这个结果记为H。接下来只需要将所有内容乘以q,这将在接下来的两个步骤中完成。
步骤3a. 取Q并与H的每个j = const层进行元素级乘法:
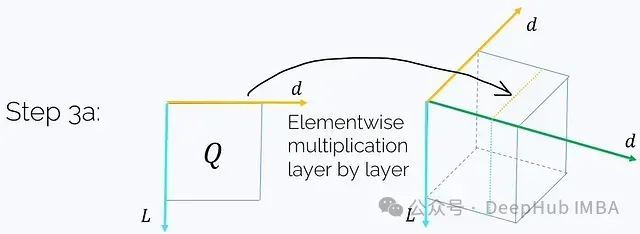
这将得到:
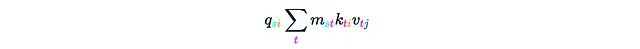
这一步骤需要O(Ld²)的时间和内存复杂度。
步骤3b. 沿i轴对结果张量求和:
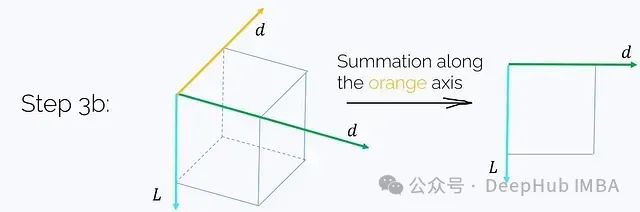
这一步骤同样需要O(Ld²)的时间和内存复杂度。最终得到了所需的结果:
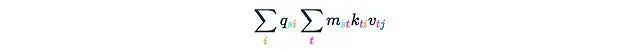
在这个过程中,最关键的是第二步,我们故意省略了其复杂度分析。一个简单的估计是:
每次矩阵乘法需要O(L²)的复杂度,重复d²次
这将导致一个巨大的O(L²d²)复杂度。但是我们的目标是选择特殊的M,使得将M乘以一个向量的复杂度为O(RL),其中R是某个不太大的常数。
例如如果M是0-1因果矩阵,那么与它相乘实际上就是计算累积和,这可以在O(L)时间内完成。但还存在许多其他具有快速向量乘法特性的结构化矩阵选项。
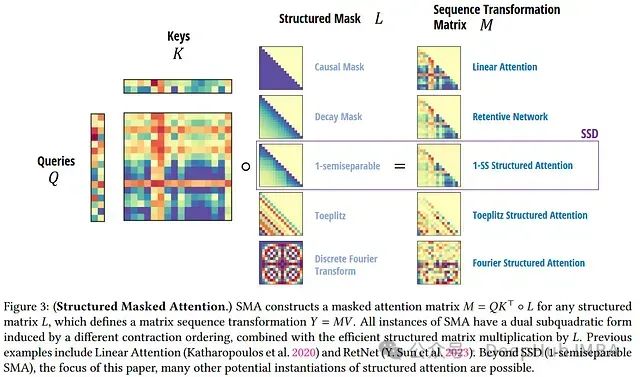
在下一节中将讨论这种矩阵类型的一个重要例子------半可分离矩阵,它与状态空间模型有着密切的联系。
半可分离矩阵与状态空间模型
让我们回顾一下(离散化的)状态空间模型(SSM)的定义。SSM是一类连接1维输入x_t、r维隐藏状态h_t和1维输出u_t的序列模型,其数学表达式如下:
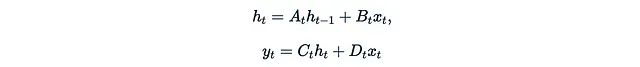
在离散形式中,SSM本质上是一个带有跳跃连接的复杂线性RNN。为了简化后续讨论,我们甚至可以通过设置D_t = 0来忽略跳跃连接。
让我们将SSM表示为单个矩阵乘法:
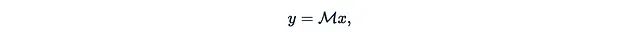
其中
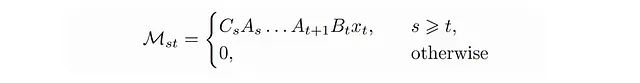
M是一个下三角矩阵,类似于我们之前讨论的注意力掩码。
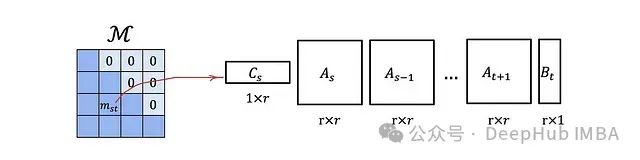
这种类型的矩阵具有一个重要的优势:
一个L × L的下三角矩阵,如果其元素可以以这种方式表示,则可以使用O(rL)的内存存储,并且具有O(rL)的矩阵-向量乘法复杂度,而不是默认的O(L²)。
这意味着每个状态空间模型都对应一个结构化的注意力掩码M,可以在具有线性化注意力的高效Transformer模型中使用。
即使没有周围的查询-键-值机制,半可分离矩阵M本身已经相当复杂和富有表现力。它本身可能就是一个掩码注意力机制。我们将在下一节中详细探讨这一点。
状态空间对偶性
在这里,我们将介绍Mamba 2论文中的一个核心结果。
让我们再次考虑y = Mu,其中u = u(x)是输入的函数,M是一个可分离矩阵。如果我们考虑一个非常特殊的情况,其中每个A_t都是一个标量矩阵:A_t = a_t I。在这种情况下公式变得特别简单:
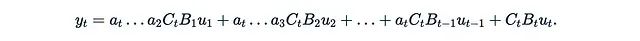
这里的

只是一个标量。还可以将C_i和B_i堆叠成矩阵B和C,使得:
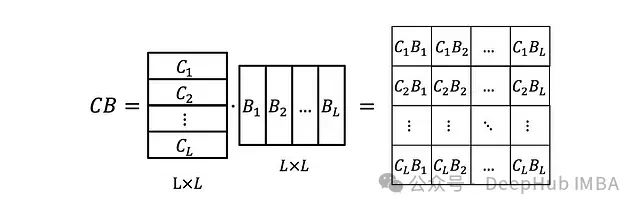
现在我们还需要定义矩阵
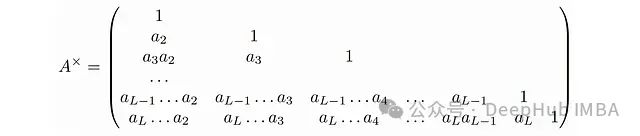
然后就可以很容易地验证:

这个表达式是否看起来很熟悉?这实际上是一个掩码注意力机制,其中:
- G作为掩码
- C作为查询矩阵Q
- B作为转置的键矩阵K^T
- u作为值矩阵V
在经典的SSM中,B和C是常量。但在Mamba模型中,它们被设计为依赖于数据,这进一步强化了与注意力机制的对应关系。这种特定状态空间模型与掩码注意力之间的对应关系在Mamba 2论文中被称为状态空间对偶性。
进一步探索
使用矩阵混合器而不是更复杂的架构并不是一个全新的idea。一个早期的例子是是MLP-Mixer,它在计算机视觉任务中使用MLP而不是卷积或注意力来进行空间混合。
尽管当前研究主要集中在大语言模型(LLM)上,但也有一些论文提出了用于编码器模型的非Transformer、矩阵混合架构。例如:
- 来自Google研究的FNet,其矩阵混合器M基于傅里叶变换。
- Hydra,除了其他创新外,还提出了半可分离矩阵在非因果(非三角)工作模式下的适应性方案。
总结
本文深入探讨了Transformer、循环神经网络(RNN)和状态空间模型(SSM)之间的潜在联系。文章首先回顾了传统的掩码自注意力机制,然后引入了线性化注意力的概念,解释了其计算效率优势。接着探讨了注意力掩码的优化,引入了半可分离矩阵的概念,并阐述了其与状态空间模型的关系。最后介绍了状态空间对偶性,揭示了特定状态空间模型与掩码注意力之间的对应关系。通过这些分析,展示了看似不同的模型架构之间存在深层联系,为未来模型设计和跨架构思想交流提供了新的视角和可能性。
https://avoid.overfit.cn/post/cc1b1bb7816b412790e9224484cd5b56
作者:Stanislav Fedotov