Bayesian Networks
1 Bayesian Networks
• A Bayesian Network (BN) represents the dependencies among variables and encodes
the full joint probability distribution concisely.
• A BN is a directed graph, where each node is annotated with probability information.
--- The set of random variables makes up the nodes of the network.
--- A set of directed links connects pairs of nodes, encoding a parent-child relationship.
--- Each node Xi has a conditional probability distribution P (Xi | P arents(Xi))
--- The graph has no directed cycles.
• Intuitively, an arrow from X to Y means that X has a direct influence on Y
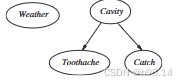
• The conditional independence of Toothache from Catch given Cavity is indicated by
the absence of a link between them.
• The network indicates that Toothache is dependent on cavity (as is catch); weather is
independent of all other variables in the network.
• A BN also has a conditional probability table (CPT) indicating the conditional
probability for each node value for a conditioning case --- the possible combination
of values for its parent nodes.
• Since each row must sum to 1, if we are dealing with boolean variables, we need only
show the positive case.
• If a variable has k parents, the table should have 2k rows.
-
贝叶斯网络(BN):
- 依赖关系与联合概率分布: 贝叶斯网络捕捉了变量集合之间的条件依赖关系,并以一种紧凑的方式编码了这些变量的完整联合概率分布。
-
有向图结构:
- 节点: 网络中的每个节点代表一个随机变量。
- 有向链接: 节点之间的有向链接表示因果关系,箭头的方向指示了影响力的流向。例如,如果从节点X到节点Y有一条箭头,这意味着X的值会影响Y的概率。
- 条件概率分布: 网络中的每个节点Xi都有一个条件概率分布P(Xi | Parents(Xi)),它指定了在给定其父节点值的情况下,Xi取不同值的概率。
- 无有向循环: 图是无环的,这意味着没有从任何节点出发通过一系列有向链接回到该节点的路径。
-
条件独立性:
- 在贝叶斯网络中,如果两个节点之间没有直接链接,给定第三个节点的情况下,这表明这两个节点在给定第三个节点的情况下是条件独立的。例如,如果"牙疼"和"探针检测"之间没有链接,在已知"蛀牙"的情况下,这意味着在蛀牙存在的情况下,牙疼的概率与探针是否检测到某物是独立的。
-
网络依赖关系:
- 网络结构表明"牙疼"依赖于"蛀牙",同样"探针检测"也依赖于"蛀牙"。这意味着牙疼的发生和探针检测到的情况都受到蛀牙存在的影响。
- "天气"与其他网络中的所有变量都是独立的,如"天气"节点没有来自其他节点的传入箭头所示。
-
条件概率表(CPT):
- 与贝叶斯网络中的每个节点相关联的是一个CPT,它提供了在给定其父节点值的情况下,节点的每个可能值的条件概率。
- 布尔变量: 对于布尔(二进制)变量,每个变量只能为真或假,CPT只需要显示变量为真的概率,因为变量为假的概率就是1减去变量为真的概率。
- 行数: 如果一个变量有k个父节点,并且每个父节点可以取两个可能值(对于布尔变量来说就是真/假),那么CPT将会有2^k行,每一行对应父节点值的一种可能组合。
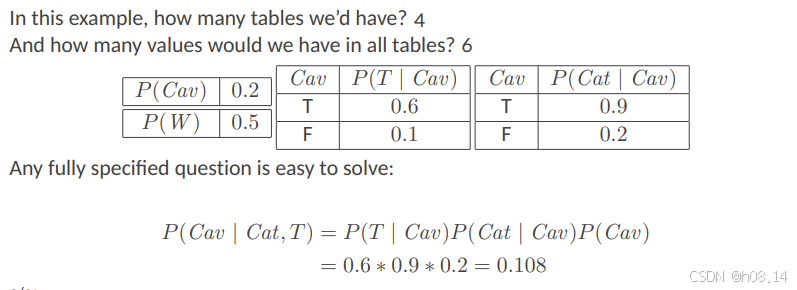
- P(T | Cav) 是在已知有蛀牙的情况下出现牙疼的条件概率,这里给出的值是 0.6。
- P(Cat | Cav) 是在已知有蛀牙的情况下,探针检测到某物的条件概率,这里给出的值是 0.9。
- P(Cav) 是蛀牙的先验概率,即在考虑任何其他信息之前,蛀牙存在的概率,这里给出的值是 0.2。
- 这个等式假设了探针检测到某物和牙疼这两个事件在给定蛀牙的情况下是条件独立的,也就是说,知道其中一个事件的发生不影响另一个事件发生的概率。这个假设使得我们可以将两个条件概率相乘,然后乘以蛀牙的先验概率来得到后验概率。

- P(Cav | Cat) 是在已知探针检测到某物的情况下存在蛀牙的后验概率。
由于我们没有关于牙疼(T)的具体信息,我们需要考虑两种情况:牙疼发生(T)和牙疼不发生(¬T)。因此,后验概率可以表示为这两种情况的概率之和:
P(Cav∣Cat)=α(P(T∣Cav)P(Cat∣Cav)P(Cav)+P(¬T∣Cav)P(Cat∣Cav)P(Cav))P(Cav∣Cat)=α(P(T∣Cav)P(Cat∣Cav)P(Cav)+P(¬T∣Cav)P(Cat∣Cav)P(Cav))
这里的α是归一化常数,它确保了所有可能情况的概率总和为1。
现在,让我们代入给定的数值:
P(Cav∣Cat)=α(0.6×0.9×0.2+0.4×0.9×0.2)P(Cav∣Cat)=α(0.6×0.9×0.2+0.4×0.9×0.2)
P(Cav∣Cat)=α(0.108+0.072)P(Cav∣Cat)=α(0.108+0.072)
P(Cav∣Cat)=α×0.18P(Cav∣Cat)=α×0.18
α的计算需要使用归一化常数,它等于1除以P(Cat),即探针检测到某物的总概率。P(Cat)可以通过以下方式计算:
P(Cat)=P(Cat∣Cav)P(Cav)+P(Cat∣¬Cav)P(¬Cav)P(Cat)=P(Cat∣Cav)P(Cav)+P(Cat∣¬Cav)P(¬Cav)
其中,P(¬Cav)是蛀牙不存在的概率,它可以通过1减去P(Cav)来计算,即:
P(¬Cav)=1−P(Cav)
因此,α可以表示为:
α=1/P(Cat)α
综上所述,α是1除以探针检测到某物的总概率,它确保了后验概率P(Cav | Cat)在所有可能情况下的总和为1。具体的数值需要根据P(Cat | ¬Cav)和P(¬Cav)来计算。
 Conditional Independence in BNs
Conditional Independence in BNs
• We just saw the numerical semantics of BNs, but we also have a "topological"
semantics:
• In a BN, each variable is conditionally independent of:
(a) Non-descendants given its parents
E.g. JohnCalls is independent of Burglary, Earthquake, and MaryCalls given Alarm
(b) All other nodes in the network given parents, children, and children's parents
(its Markov Blanket)
E.g. Burglary is independent of JohnCalls and MaryCalls, given Alarm and Earthquake




