
================================
分享 一篇 J. Phys. Chem. C:机器学习模型的结构嵌入方法加速堆叠二维材料的研究的文章 。
感谢论文的原作 者 !
================================
主要内容
"二维材料的性能可以通过堆叠进行高自由度控制,因此探索堆叠二维(2D)材料的结构与性能之间的关系至关重要。然而,高自由度造成的大物质空间和莫尔效应造成的大系统使得密度泛函理论(DFT)计算非常昂贵。在这里,为了加速对堆叠二维材料的研究,我们开发了一种用于机器学习模型的结构嵌入方法,该方法平等地对待层内键合相互作用和层间非键合相互作用。该方法的性能明显优于其他传统的边缘嵌入方法。排列重要性分析表明,电子显着影响堆叠二维材料的性能。由于结构嵌入方法精度的提高,我们使用结构嵌入PAINN(SE-PAINN)来预测扭曲堆叠二维材料的结合能和带隙,基本再现了DFT计算结果,而计算成本为减少了几个数量级。结构嵌入方法使得研究堆叠二维材料的扭转特性成为可能。SE-PAINN在势能面预测方面也显示出了良好的应用前景。这项工作提出了一种结构嵌入方法来可靠地预测层状堆叠二维材料的性能,这将为研究扭曲堆叠二维材料开辟一条重要途径。"------取自文章摘要。
================================

================================
Figure 1
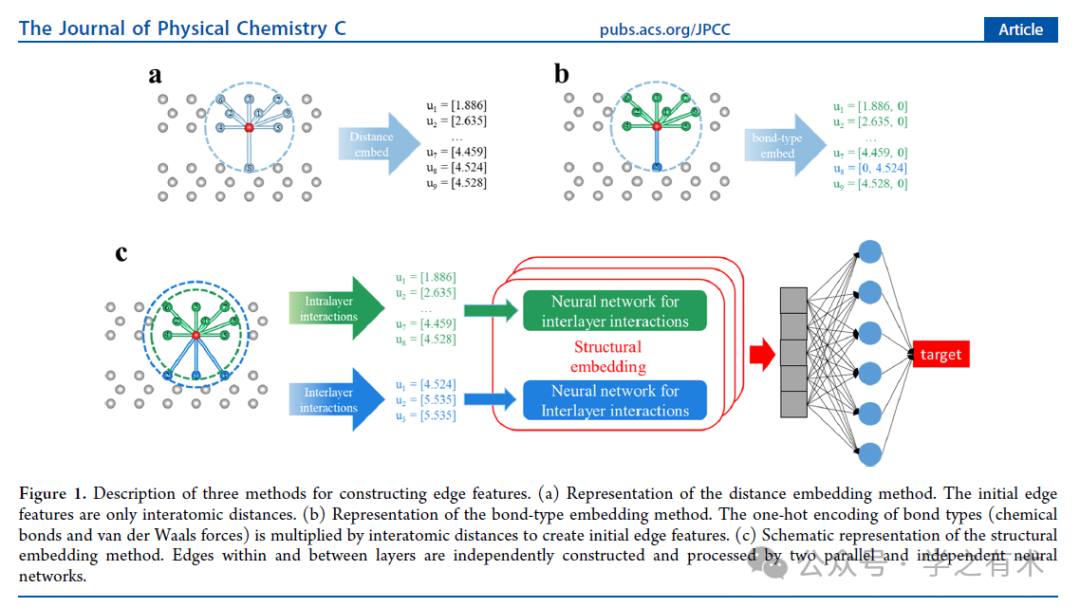
Figure 2
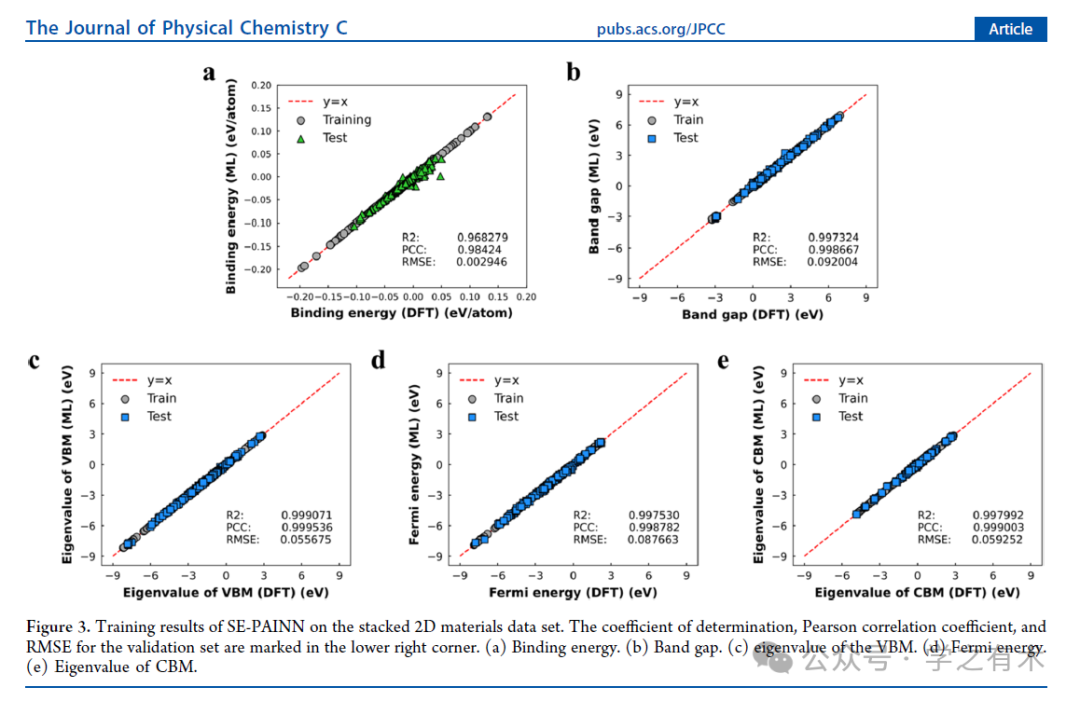
Figure 3
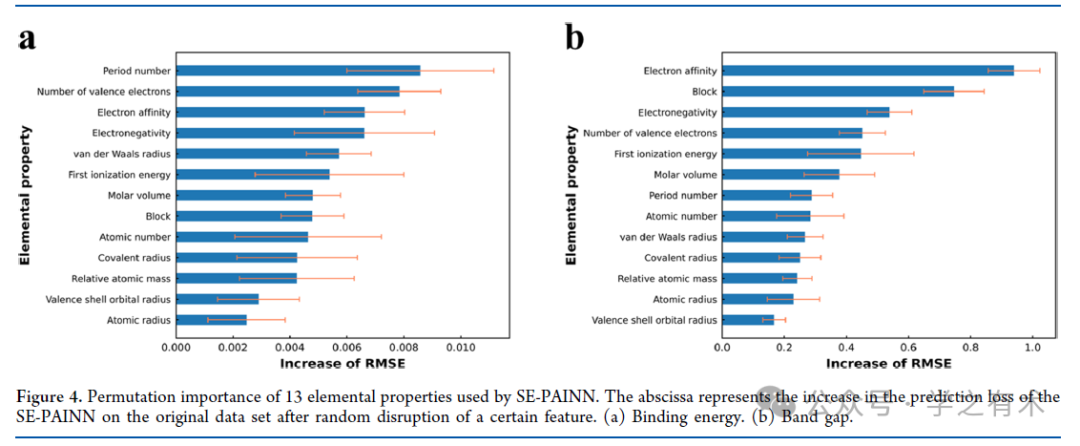
Figure 4
================================
以上是我们分享的一些经验或者文章的搬运,或有不足,欢迎大家指出。若留言未回复,重要的消息可以留言再提醒一下,因为超过48小时不可回复。
如有侵权,请联系我们立马删除!
👇
文章题目:
Structural Embedding Methods for Machine Learning Models Accelerate Research on Stacked 2D Materials
👇