＜刷题笔记＞力扣236题——二叉树的公共祖先

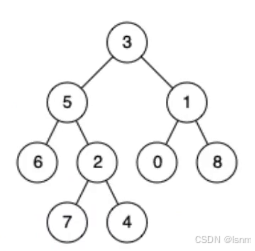
题目解释：

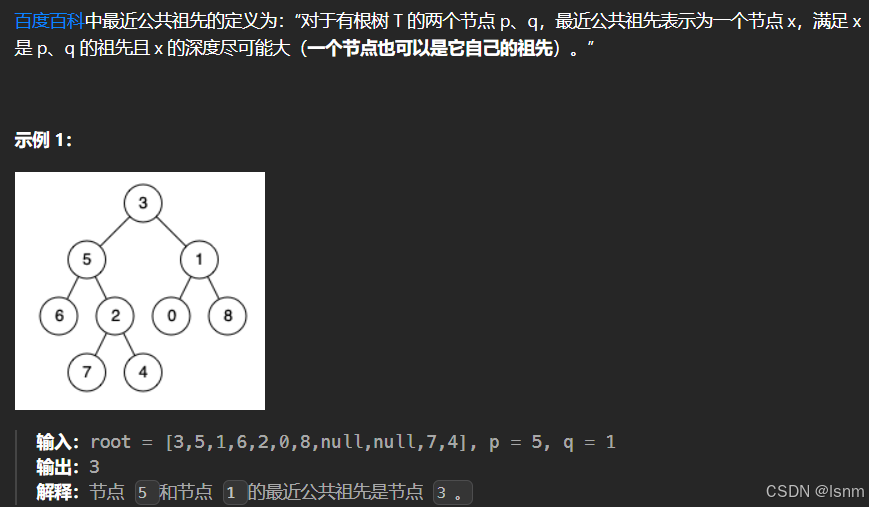
我们以这棵树为例，来观察找不同的最近公共祖先有何特点：

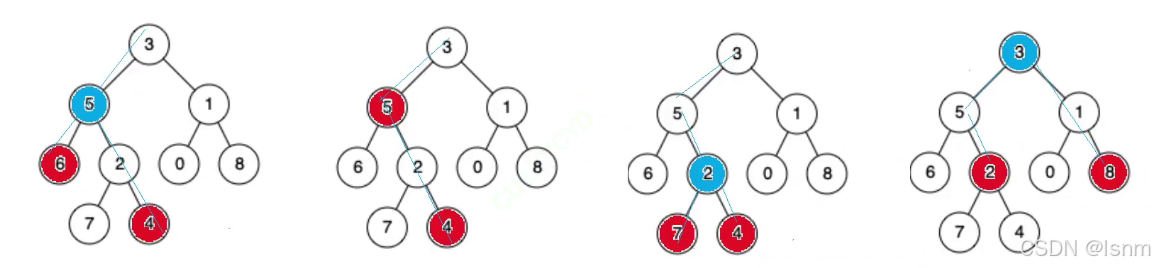
思路一：

除了第二种情况，最近公共祖先满足：一个节点在他的左边，一个节点在他的右边。

并且，其他公共祖先不满足这个条件，只有最近公共祖先满足这一点。

所以我们可以利用这个逻辑来破题：从根节点开始往下查找，找到的第一个满足"p和q分别在他的左右两侧的节点"，就是要找的最近公共祖先。

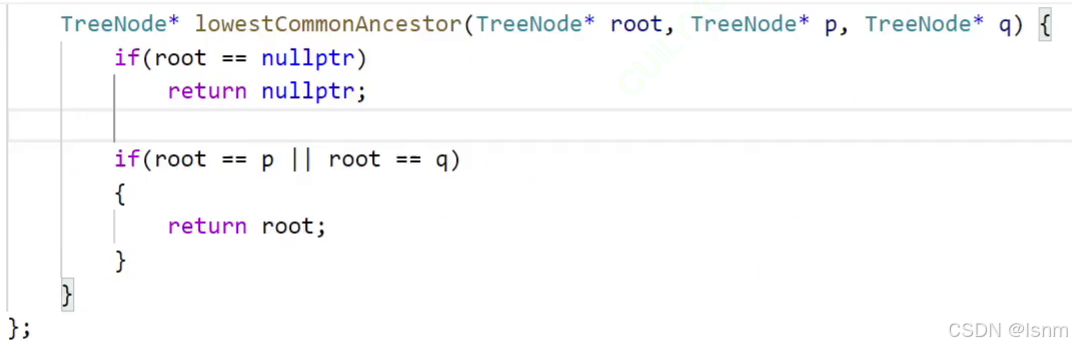
先来特殊处理第二种情况：

然后涉及到最关键的步骤：

分别用bool值封装q和p找位置的函数，便于依次罗列出q和p对于当前节点的位置（是否满足一左一右）

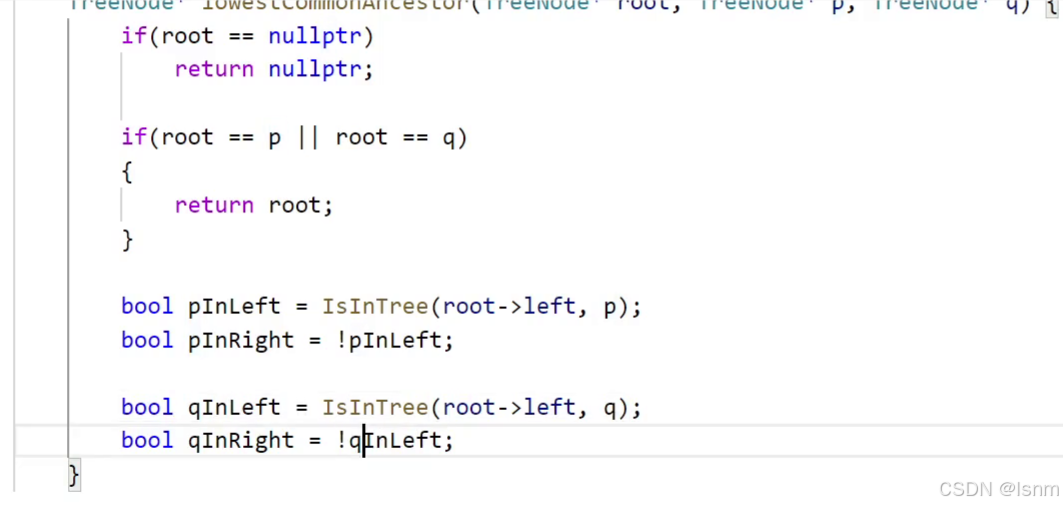
实现IsInTree：

完整代码：

cpp 复制代码

bool IsInTree(TreeNode* tree,TreeNode* k){
        if(tree==nullptr) return false;
        return tree==k
            || IsInTree(tree->left,k)
            || IsInTree(tree->right,k);
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
       //特殊处理本身存在爷孙或父子关系的情况
        if(root == p || root == q){
            return root;
        }
        //罗列出p和q是否存在的条件
        bool PInLeft = IsInTree(root->left,p);
        bool PInRight = !PInLeft;
        bool QInLeft = IsInTree(root->left,q);
        bool QInRight = !QInLeft;
        //分类讨论
        if((PInLeft && QInRight) || (QInLeft && PInRight)){
            return root;
        }else if(PInLeft && QInLeft){
            return lowestCommonAncestor(root->left,p,q);
        }else{
            return lowestCommonAncestor(root->right,p,q);
        }
        //return nullptr;
    }
};

但是实际运行速度并不理想：运行速度几乎都要接近一秒了

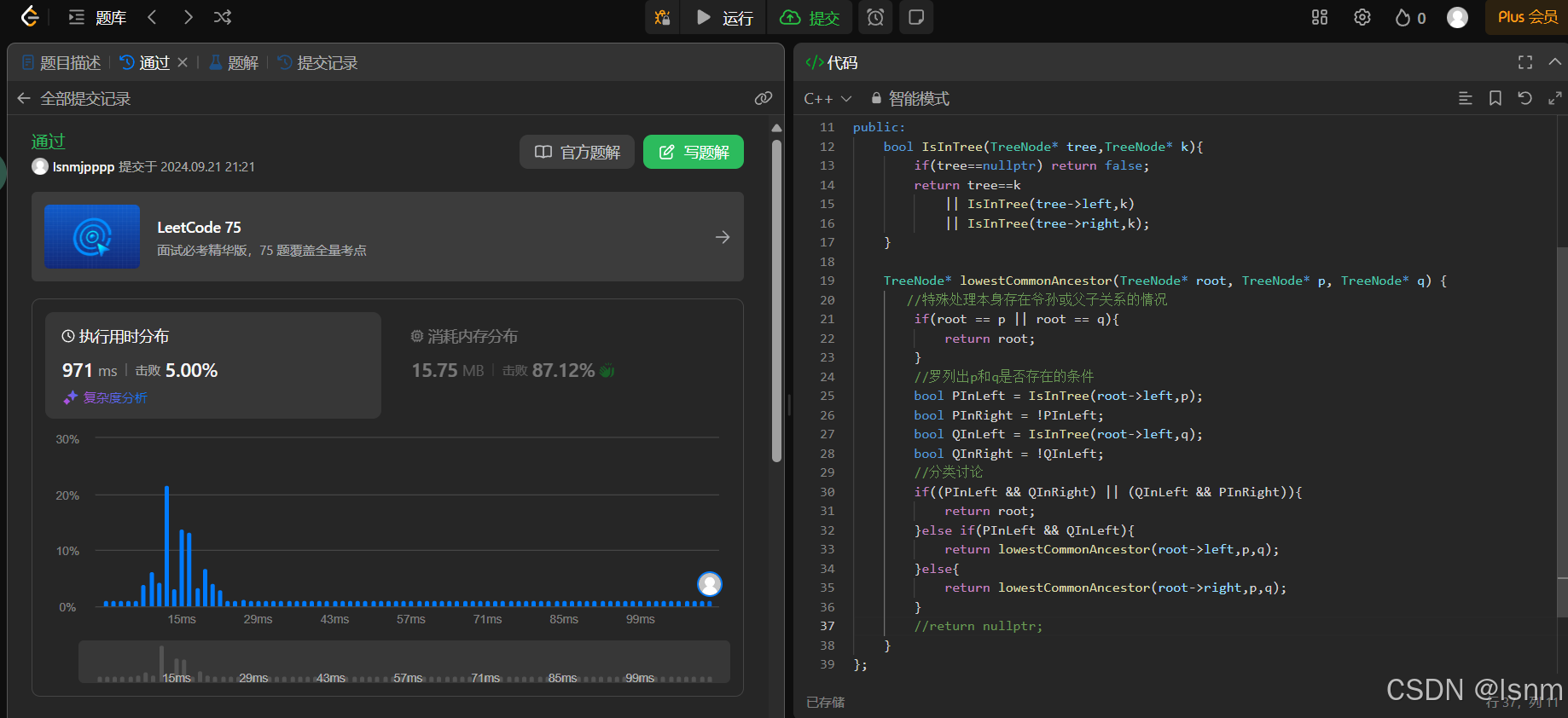
这样操作的时间复杂度是O(N^2)：

因为我们的树是一个毫无数据存放逻辑的任意形状的二叉树。所以，每一次去判断IsInTree都是把当前root下面的数据都遍历一遍，因此其本质其实是：第一遍从3开始查左查右，第二次从5开始查左查右，再从6开始查左查右......

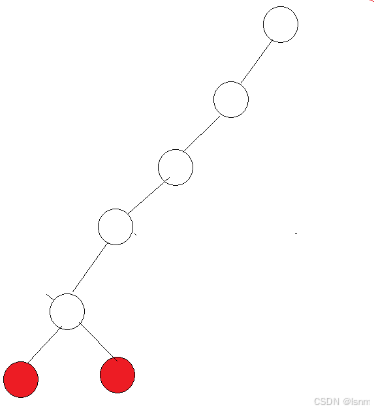
如果遇到最坏的如下图一样的环境：

其时间复杂度是O(N^2)

当然，如果越接近完全二叉树的情形，时间复杂度越低，最理想能达到O(n)

思路二：

如果我们能根据找祖先的两个节点往回走，一切都会很好解决。

这样就变成了两条相交链表找交点。

使用前序查找+栈来找记录路径，然后再进行一次"两条相交链表找交点"

比如这张图，要找7，那么我们的路径应该记录为：3-5-2-7

在遇到6这样的错误的分支方向时，我们先将其入栈，发现他不对就出栈。

cpp 复制代码

class Solution {
public:
    bool FindPath( stack<TreeNode*>& st , TreeNode* des , TreeNode* root){
        if(root==nullptr) {
            return false;
        }
        st.push(root);
        if(root == des){
            return true;
        }else if((!FindPath(st,des,root->left))&&
                 (!FindPath(st,des,root->right))){
                  st.pop();
                  return false;
                }
            return true;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> q_path;
        stack<TreeNode*> p_path;
        FindPath(q_path,q,root);
        FindPath(p_path,p,root);

        while(q_path.size()!=p_path.size()){
            if(q_path.size()>p_path.size()) q_path.pop();
            if(p_path.size()>q_path.size()) p_path.pop();
        }

        while(q_path.top()!=p_path.top()){
            q_path.pop();
            p_path.pop();
        }

        return q_path.top();
    }
};

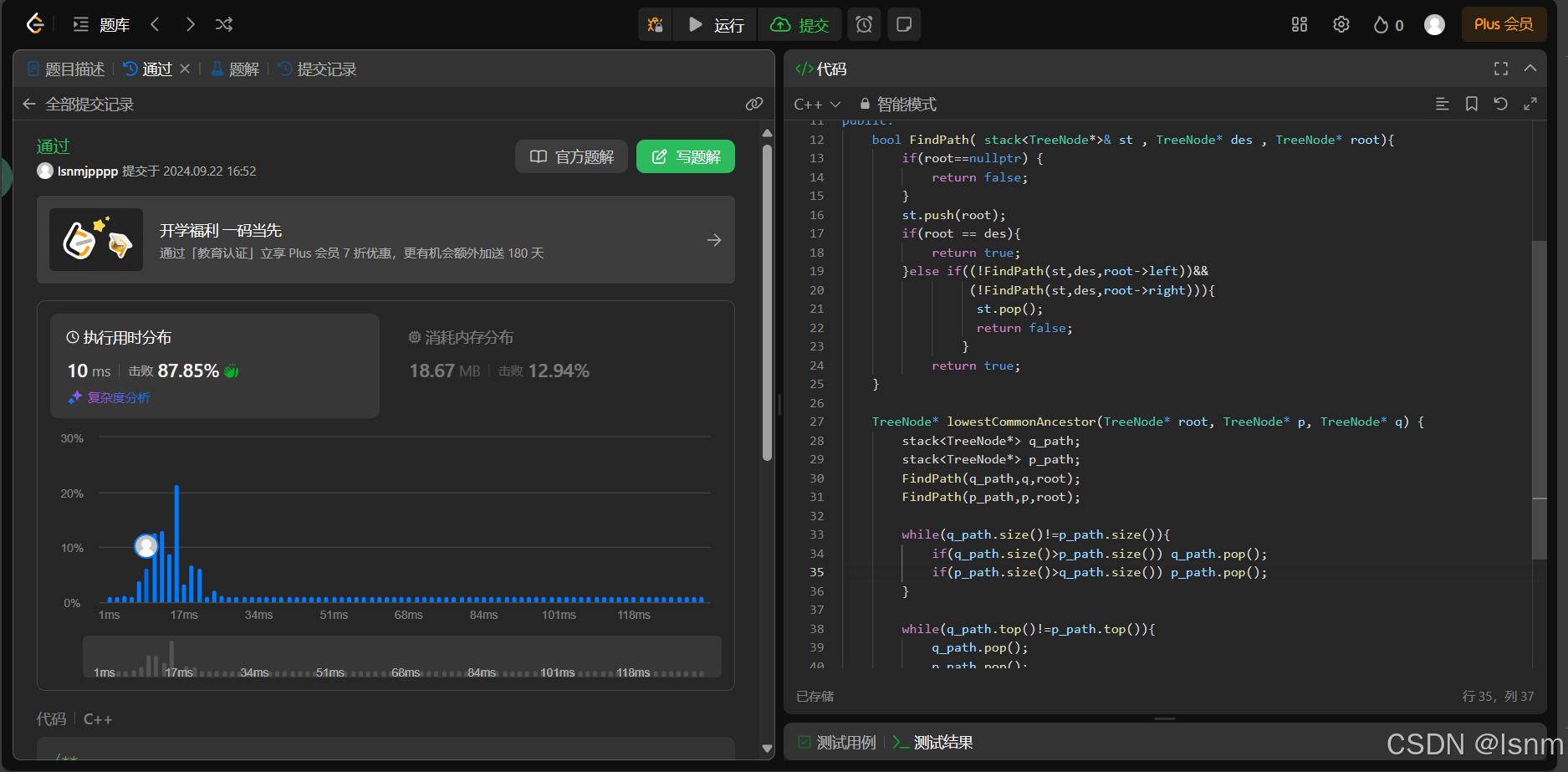
可以发现现在这种方法提升了不少速度：

欢迎各位看官在评论区写出对这道题的其他解法。

＜刷题笔记＞ 力扣236题——二叉树的公共祖先

思路一：

思路二：

＜刷题笔记＞力扣236题——二叉树的公共祖先