1.数字图像处理:空间域滤波
1.1 滤波器核(相关核)与卷积

图像上的邻域计算

线性空间滤波的原理


滤波器核(相关核)是如何得到的?
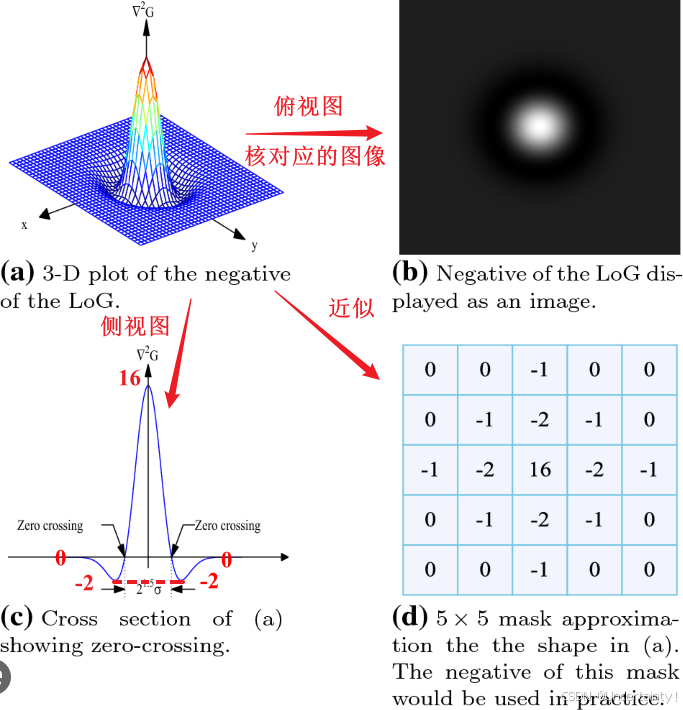
空间域的卷积



卷积:滤波器核与window中的对应值相乘后所有值相加得到一个像素值,滑动窗口遍历整个图像




滤波器核(相关核)与卷积的区别


截图来源:【小动画】彻底理解卷积【超形象】卷的由来,小元老师




滤波器核对称时,翻转与不翻转没有影响,所以卷积等于相关性


卷积的物理实质可以通过以下几个方面进行理解,这些方面涉及到信号处理、系统响应和图像处理等领域

1.2 图像加噪

噪声点的判定标准

由灰度直方图得到概率密度函数的方法





从含噪图像中确定具体噪声模型的系统化方法?

选取实验用的实验图像,完成图像读取和显示,给图像加上高斯噪声
python
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 打开图片并转换为灰度图像
img_dir = r'D:\Document\Experiment\data\image1.jpg'
# 读取图像并转换为灰度
gray = cv.imread(img_dir, 0)
image_array = np.array(gray)
# 定义高斯噪声的参数
mean = 0 # 均值
sigma = 80 # 标准差(调整噪声强度)
# 生成高斯噪声
gaussian_noise = np.random.normal(mean, sigma, image_array.shape)
# 将噪声加入图像
noisy_image = image_array + gaussian_noise
# 将噪声后的图像剪裁到0-255范围内,并转换为uint8
noisy_image_clipped = np.clip(noisy_image, 0, 255).astype(np.uint8)
# 显示原图和加入噪声后的图像
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.title('Original Image')
plt.imshow(image_array, cmap='gray')
plt.subplot(1,2,2)
plt.title('Noisy Image')
plt.imshow(noisy_image_clipped, cmap='gray')
plt.show()
1.3 均值滤波、高斯滤波、中值滤波
均值滤波

高斯滤波



中值滤波


为了使得卷积能够正常进行,对原图像外围进行填充(padding)

用自己编写的滤波函数分别对实验图像进行滤波;
python
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 读取图像并转换为灰度
img_dir = r'D:\Document\Experiment\data\image1.jpg' # 图像路径
gray = cv.imread(img_dir, 0) # 读取图像,并将其转换为灰度图像
# 定义高斯噪声的参数
mean = 0 # 高斯噪声的均值
sigma = 80 # 高斯噪声的标准差,用于控制噪声强度
# 生成高斯噪声并添加到图像
gaussian_noise = np.random.normal(mean, sigma, gray.shape) # 生成与图像相同大小的高斯噪声
noisy_image = gray + gaussian_noise # 将生成的噪声添加到图像
noisy_image_clipped = np.clip(noisy_image, 0, 255).astype(np.uint8) # 将噪声叠加后的图像值限制在0到255,并转换为uint8类型
# 均值滤波实现
# 其中,均值滤波一般的具体实现步骤是:
# .选择一个(2n+l) x (2n+l)的窗口(通常为3 x 3或5 x 5),并用该窗口沿图像数据进行行或列的滑动;
# .读取窗口下各对应像素的灰度值;
# .求取这些像素的灰度平均值替代窗口中心位置的原始像素灰度值。
def mean_filter(image, kernel_size=3):
# 填充大小
# 根据传入的窗口大小 kernel_size 计算需要的填充尺寸
# 因为均值滤波会涉及到窗口的滑动,所以为了保持输出图像的尺寸与输入图像相同,需要在图像的边缘进行填充。对于 3x3 的窗口,pad_size 为 1;对于 5x5 的窗口,pad_size 为 2
pad_size = kernel_size // 2 # 根据核大小计算需要的填充尺寸
# 使用 np.pad 函数将原始图像进行填充,pad_size 为填充的边界大小,mode='constant' 指定使用常数值填充,constant_values=0 表示用 0 填充。这使得在处理图像边缘时能够避免索引超出边界的错误。
padded_image = np.pad(image, pad_size, mode='constant', constant_values=0) # 用常数0填充图像边缘
# 创建一个与输入图像 image 形状相同的全零数组 output_image,用于存储均值滤波后的结果。
output_image = np.zeros_like(image) # 初始化输出图像,大小与原图一致
# 滑动窗口进行均值滤波
# 外层循环:通过 for 循环遍历填充后的图像的行,从 pad_size 开始到 padded_image.shape[0] - pad_size 结束。这样做是为了避免在处理图像边缘时出现越界
for i in range(pad_size, padded_image.shape[0] - pad_size):
# 内层循环:同样通过 for 循环遍历填充后的图像的列,范围与行的处理相同。这两个嵌套循环用于对图像的每一个像素进行处理
for j in range(pad_size, padded_image.shape[1] - pad_size):
# 获取窗口内的像素:通过切片操作从填充后的图像中获取当前窗口的像素值。窗口的大小为 (kernel_size, kernel_size),即从 (i-pad_size, j-pad_size) 到 (i+pad_size, j+pad_size) 的区域
window = padded_image[i-pad_size:i+pad_size+1, j-pad_size:j+pad_size+1] # 获取窗口内的像素
# 使用 np.mean(window) 计算窗口中像素值的平均值,并将结果赋值给输出图像 output_image 的对应位置。为了保持位置一致性,索引使用 i-pad_size 和 j-pad_size
output_image[i-pad_size, j-pad_size] = np.mean(window) # 计算窗口像素的平均值,并赋给输出图像的对应位置
return output_image # 返回滤波后的图像
# 高斯滤波实现
# 高斯滤波一般的具体实现步骤是:
# .选择一个(2n+l) x (2n+l)的窗口(通常为3 x 3或5 x 5),生成二维高斯模板,并用该窗口沿图像数据进行行或列的滑动;
# .读取窗口下各对应像素的灰度值;
# .求取这些像素与二维高斯模板对应位置元素的乘积再求和,用该值替代窗口中心位置的原始像素灰度值。
def gaussian_kernel(kernel_size=3, sigma=1.0):
k = kernel_size // 2 # 计算高斯核中心的偏移
gaussian_kernel = np.zeros((kernel_size, kernel_size), dtype=np.float32) # 初始化高斯核
for x in range(-k, k + 1): # 遍历核的行坐标
for y in range(-k, k + 1): # 遍历核的列坐标
gaussian_kernel[x + k, y + k] = np.exp(-(x**2 + y**2) / (2 * sigma**2)) # 根据高斯公式计算权重
gaussian_kernel /= (2 * np.pi * sigma**2) # 归一化常数
gaussian_kernel /= gaussian_kernel.sum() # 对高斯核进行归一化,使其所有元素的和为1
return gaussian_kernel # 返回生成的高斯核
def gaussian_filter(image, kernel_size=3, sigma=1.0):
pad_size = kernel_size // 2 # 计算填充大小
padded_image = np.pad(image, pad_size, mode='constant', constant_values=0) # 用常数0填充图像边缘
output_image = np.zeros_like(image) # 初始化输出图像
kernel = gaussian_kernel(kernel_size, sigma) # 生成高斯核
# 滑动窗口进行高斯滤波
for i in range(pad_size, padded_image.shape[0] - pad_size):
for j in range(pad_size, padded_image.shape[1] - pad_size):
window = padded_image[i-pad_size:i+pad_size+1, j-pad_size:j+pad_size+1] # 获取窗口内的像素
output_image[i-pad_size, j-pad_size] = np.sum(window * kernel) # 计算窗口像素与高斯核的加权和
return output_image # 返回滤波后的图像
# 中值滤波实现
# 中值滤波一般的具体实现步骤是:
# .选择一个(2n+l)x(2n+l)的窗口(通常为3x3或5x5),并用该窗口沿图像数据进行行或列的滑动;
# .读取窗口下各对应像素的灰度值;
# .将这些灰度值从小到大排成一列,用排序所得的中值替代窗口中心位置的原始像素灰度值;
def median_filter(image, kernel_size=3):
pad_size = kernel_size // 2 # 计算填充大小
padded_image = np.pad(image, pad_size, mode='constant', constant_values=0) # 用常数0填充图像边缘
output_image = np.zeros_like(image) # 初始化输出图像
# 滑动窗口进行中值滤波
for i in range(pad_size, padded_image.shape[0] - pad_size):
for j in range(pad_size, padded_image.shape[1] - pad_size):
# 获取窗口内的像素
window = padded_image[i-pad_size:i+pad_size+1, j-pad_size:j+pad_size+1]
output_image[i-pad_size, j-pad_size] = np.median(window) # 计算窗口像素的中值,并赋给输出图像的对应位置
return output_image # 返回滤波后的图像
# 进行均值滤波、高斯滤波、中值滤波
mean_filtered_img = mean_filter(noisy_image_clipped, kernel_size=3) # 应用均值滤波,使用3x3窗口
gaussian_filtered_img = gaussian_filter(noisy_image_clipped, kernel_size=3, sigma=1.0) # 应用高斯滤波,使用3x3窗口,sigma为1.0
median_filtered_img = median_filter(noisy_image_clipped, kernel_size=3) # 应用中值滤波,使用3x3窗口
# 定义运算及其标题
operations = [
("Original", gray), # 原始图像
("Noised", noisy_image_clipped), # 添加噪声后的图像
("Mean Filter", mean_filtered_img), # 均值滤波后的图像
("Gaussian Filter", gaussian_filtered_img), # 高斯滤波后的图像
("Median Filter", median_filtered_img) # 中值滤波后的图像
]
# 绘图
plt.figure(figsize=(15, 7)) # 设置绘图窗口大小
for i, (title, result) in enumerate(operations, 1): # 遍历运算结果
plt.subplot(2, 3, i) # 创建子图,2行3列
plt.title(title) # 设置子图标题
plt.imshow(result, cmap='gray') # 显示图像,使用灰度颜色映射
plt.axis('off') # 关闭坐标轴显示
plt.tight_layout() # 自动调整子图布局,使之不重叠
plt.show() # 显示图像
用OpenCV自带的滤波函数对实验图像分别进行滤波;
python
# (4)用OpenCV自带的滤波函数对实验图像分别进行滤波;
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 读取图像并转换为灰度
img_dir = r'D:\Document\Experiment\data\image1.jpg'
gray = cv.imread(img_dir, 0)
# 灰度加噪(添加高斯噪声)
mean = 0 # 均值
sigma = 80 # 标准差(调整噪声强度)
gaussian_noise = np.random.normal(mean, sigma, gray.shape) # 生成高斯噪声
noisy_image = gray + gaussian_noise # 将噪声加入图像
noisy_image_clipped = np.clip(noisy_image, 0, 255).astype(np.uint8) # 剪裁到0-255范围并转换为uint8
# 均值滤波实现
def mean_filter(image, kernel_size=5):
# 使用cv2的blur函数进行均值滤波
return cv.blur(image, (kernel_size, kernel_size))
# 高斯滤波实现
def gaussian_filter(image, kernel_size=5, sigma=1.0):
# 使用cv2的GaussianBlur函数进行高斯滤波
return cv.GaussianBlur(image, (kernel_size, kernel_size), sigma)
# 中值滤波实现
def median_filter(image, kernel_size=5):
# 使用cv2的medianBlur函数进行中值滤波
return cv.medianBlur(image, kernel_size)
# 进行均值滤波、高斯滤波、中值滤波
mean_filtered_img = mean_filter(noisy_image_clipped)
gaussian_filtered_img = gaussian_filter(noisy_image_clipped)
median_filtered_img = median_filter(noisy_image_clipped)
# 定义运算及其标题
operations = [
("Original", gray),
("Noised", noisy_image_clipped),
("Mean Filter", mean_filtered_img),
("Gaussian Filter", gaussian_filtered_img),
("Median Filter", median_filtered_img)
]
# 绘图
plt.figure(figsize=(15, 7))
for i, (title, result) in enumerate(operations, 1):
plt.subplot(2, 3, i)
plt.title(title)
plt.imshow(result, cmap='gray')
plt.axis('off') # 关闭坐标轴显示
plt.tight_layout()
plt.show()