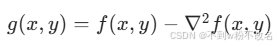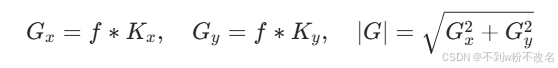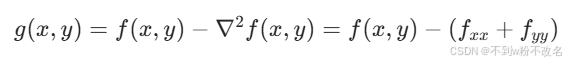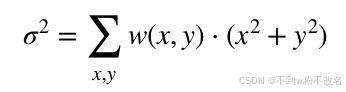目录
[(一)线性滤波器(Linear Filter)](#(一)线性滤波器(Linear Filter))
[(二)非线性滤波器(Non-linear Filter)](#(二)非线性滤波器(Non-linear Filter))
[中值滤波(Median Filter)](#中值滤波(Median Filter))
[最大值 / 最小值滤波](#最大值 / 最小值滤波)
[1. 定义与本质](#1. 定义与本质)
[2. 典型滤波器及原理](#2. 典型滤波器及原理)
[3. 应用场景](#3. 应用场景)
[1. 定义与本质](#1. 定义与本质)
[2. 典型滤波器及原理](#2. 典型滤波器及原理)
[3. 应用场景](#3. 应用场景)
1、下面的滤波器哪些可作为图像平滑滤波器,哪些可作为图像锐化滤波器?为什么?
问题1:以下两个滤波器属于平滑滤波器还是锐化滤波器?为什么?
问题2:下面2个高斯滤波器对图像平滑,哪个滤波器使图像平滑后更模糊?为什么?
一、空域滤波基础
一、空域滤波的基本概念
空域滤波(Spatial Filtering) 是图像处理中最基础的操作之一,其核心思想是通过对图像像素及其邻域进行局部运算 来修改图像的像素值。与频域滤波(基于傅里叶变换处理频率成分)不同,空域滤波直接在图像的空间域上进行操作,主要通过滤波器(Filter) 或模板(Kernel) 实现。
二、空域滤波的数学原理
-
核心操作:卷积(Convolution)
空域滤波的本质是滤波器与图像的卷积运算。对于一幅图像 f(x,y) 和一个大小为 m×n 的滤波器 h(x,y),输出图像 g(x,y) 的计算方式为:
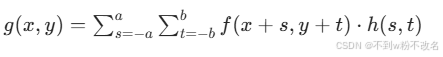
其中 (a,b) 为滤波器中心坐标,通常取 m=2a+1,n=2b+1(奇数大小便于定位中心)。

-
滤波器滑动过程
- 滤波器从图像左上角开始,以像素为步长逐行滑动。
- 每个位置上,滤波器中心与当前像素对齐,计算邻域像素与滤波器权重的乘积和,作为输出像素值。
三、空域滤波器的分类与典型示例
(一)线性滤波器(Linear Filter)
基于线性加权求和,满足叠加原理,主要用于平滑去噪或模糊处理。
| 滤波器类型 | 核心特点 | 典型模板(3×3) | 应用场景 |
|---|---|---|---|
| 均值滤波 | 简单平均邻域像素值,降低噪声但模糊边缘。 | 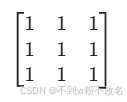 |
去除高斯噪声、图像模糊 |
| 高斯滤波 | 基于高斯分布加权,中心像素权重高,边缘权重低,平滑效果更自然。 | 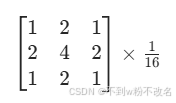 |
图像去噪、高斯模糊、边缘检测前预处理 |
| 加权平均滤波 | 自定义权重,可针对特定方向或特征增强,如边缘保持滤波(EPF)。 | 自定义权重矩阵,如边缘方向加权 | 保留细节的同时去噪 |
(二)非线性滤波器(Non-linear Filter)
不满足线性叠加原理,通过排序、取极值等操作处理像素,更适合去除脉冲噪声(如椒盐噪声)。
中值滤波(Median Filter)
- 原理:将邻域像素值排序后取中值,替换中心像素。
- 模板示例(3×3):将 9 个像素值排序,取第 5 大的值。
- 特点:有效去除椒盐噪声,同时保留边缘(相比均值滤波)。
最大值 / 最小值滤波
- 最大值滤波:取邻域最大值,增强亮区域,适用于突出亮点(如检测光斑)。
- 最小值滤波:取邻域最小值,增强暗区域,适用于去除亮噪声(如盐噪声)。
四、空域滤波的应用场景
图像去噪
- 线性滤波(如高斯滤波)适合处理高斯噪声(连续分布噪声)。
- 非线性滤波(如中值滤波)适合处理脉冲噪声(离散噪声点)。
边缘检测预处理
高斯滤波常用于模糊图像,减少噪声对边缘检测的干扰(如 Canny 算子前的高斯平滑)。
特征增强与抑制
- 锐化滤波(如拉普拉斯算子)通过增强像素梯度突出边缘,公式为:
其中 ∇2f 为拉普拉斯算子,典型模板:图像模糊与降采样
均值滤波或高斯滤波常用于图像缩放前的预处理,减少锯齿效应。
五、空域滤波的关键参数与影响
滤波器大小
- 小尺寸(3×3、5×5):保留细节,去噪能力弱。
- 大尺寸(7×7 及以上):去噪能力强,但过度模糊图像,丢失细节。
权重分布
- 线性滤波器的权重决定了对不同位置像素的敏感度(如高斯滤波的中心权重更高)。
- 非线性滤波器的操作逻辑(如排序取中值)决定了对异常值的鲁棒性。
六、空域与频域滤波的对比
| 维度 | 空域滤波 | 频域滤波 |
|---|---|---|
| 处理空间 | 直接在像素空间操作,直观易理解。 | 基于傅里叶变换,处理频率成分。 |
| 计算复杂度 | 复杂度低,适合实时处理(尤其小模板)。 | 需进行傅里叶变换,计算开销大。 |
| 典型应用 | 去噪、边缘检测、局部特征增强。 | 全局频率成分调整(如高通 / 低通滤波)。 |

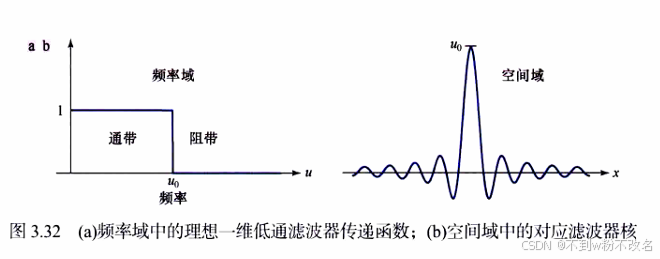
七、总结
空域滤波是图像处理的基石,通过设计不同的滤波器模板,可实现去噪、模糊、锐化等多种效果。理解其数学原理(如卷积运算)和滤波器特性(线性 / 非线性),有助于根据实际需求(如图像噪声类型、处理目标)选择合适的滤波方法。实际应用中,常需结合滤波器大小、权重设计与多次实验,平衡去噪效果与细节保留。
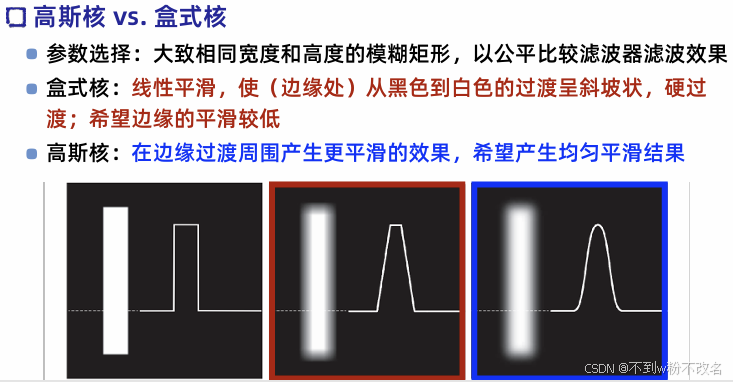
二、平滑空间滤波器
平滑空间滤波器:去噪与模糊的核心工具
1. 定义与本质
平滑滤波通过邻域像素加权平均 减少局部像素值波动,本质是低通滤波(抑制高频,保留低频)。
作用效果:去除图像中的噪声(如高斯噪声、椒盐噪声),模糊细节(如平滑纹理、弱化边缘)。
2. 典型滤波器及原理
| 滤波器类型 | 原理描述 | 公式 / 模板示例 | 特点与应用场景 |
|---|---|---|---|
| 均值滤波 | 邻域像素值算术平均,权重均匀分布。 | 3×3 模板: 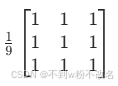 |
简单高效,但易模糊边缘,适合轻度高斯噪声。 |
| 高斯滤波 | 基于高斯函数加权,中心像素权重最大,离中心越远权重越小。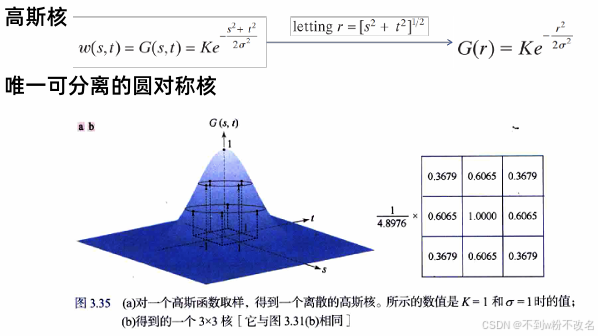 |
二维高斯核: 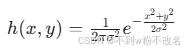 |
平滑效果更自然,可通过调整 σ 控制模糊程度,常用于图像预处理(如 CNN 前的降采样)。 |
| 中值滤波 | 取邻域像素值的中值替代中心像素,属于非线性滤波。 | 操作:排序邻域像素,取中间值。 | 对椒盐噪声(脉冲噪声)效果极佳,能保护边缘(因不依赖加权平均)。 |
| 双边滤波 | 同时考虑像素空间距离和灰度差异的加权平均,属于保边平滑。 | 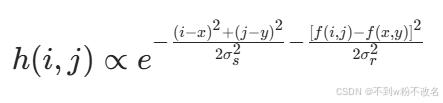 |
保留边缘的同时去除噪声,常用于人像磨皮(保留轮廓,平滑皮肤)。 |
3. 应用场景
- 噪声去除:医学影像(CT/MRI)去噪、卫星图像去云雾干扰。
- 图像预处理:降低图像分辨率前的平滑,避免锯齿效应(如双线性插值前的高斯滤波)。
- 风格化处理 :油画效果、卡通化中的背景模糊。
三、锐化空间滤波器
锐化空间滤波器:边缘增强与细节提取
1. 定义与本质
锐化滤波通过增强像素梯度变化 突出边缘和细节,本质是高通滤波(抑制低频,保留高频)。
作用效果:使模糊图像变清晰,强化物体轮廓(如文字边缘、细胞边界),提升图像对比度。
2. 典型滤波器及原理
| 滤波器类型 | 原理描述 | 公式 / 模板示例 | 特点与应用场景 |
|---|---|---|---|
| 梯度算子(一阶导数) | 通过计算像素灰度梯度值增强边缘,常用算子包括 Sobel、Prewitt、Roberts。 | Sobel 算子(x 方向):  |
对水平 / 垂直边缘敏感,输出为梯度幅值,常用于边缘检测(如 Canny 算法前处理)。 |
| 拉普拉斯算子(二阶导数) | 计算像素邻域的二阶导数,边缘处二阶导数值为零(过零点),用于定位边缘位置。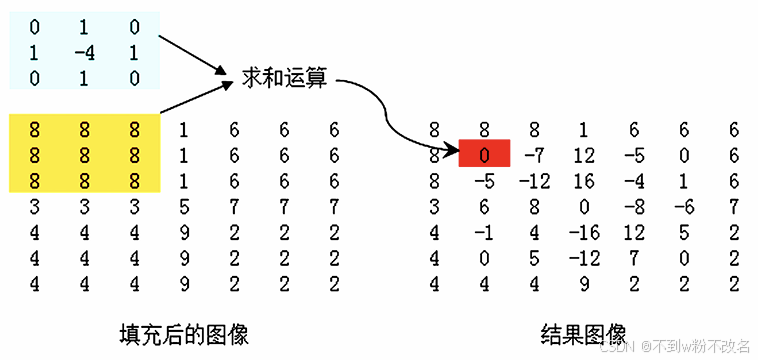 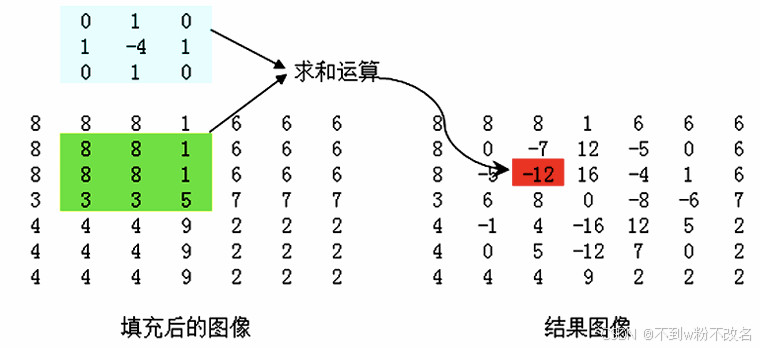 |
4×4 拉普拉斯模板:  |
对噪声敏感(因强化高频),常与原图叠加使用(锐化 = 原图 + 拉普拉斯结果)。 |
| 非锐化掩模(Unsharp Mask) | 先模糊图像,再用原图减去模糊图,得到高频细节增强的结果。 | 流程: 1. 高斯模糊  2. 掩模 2. 掩模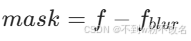 3. 锐化结果 fsharp=f+k⋅mask 3. 锐化结果 fsharp=f+k⋅mask |
效果自然,广泛用于摄影后期(如风光片增强岩石纹理)。 |
| 高提升滤波(High Boost Filter) | 非锐化掩模的增强版,通过调整权重突出特定频率成分。 | 公式: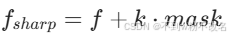 (k>1 时增强效果更明显) (k>1 时增强效果更明显) |
可自定义增强强度,适合需要突出微小细节的场景(如显微图像)。 |
3. 应用场景
- 边缘检测:医学图像中的器官轮廓提取、文档扫描中的文字边缘强化。
- 图像增强:老照片修复(锐化模糊的人像边缘)、遥感图像中的地形轮廓突出。
- 特征提取:计算机视觉中预处理步骤(如车牌识别前的边缘增强)。
四、平滑与锐化的核心区别对比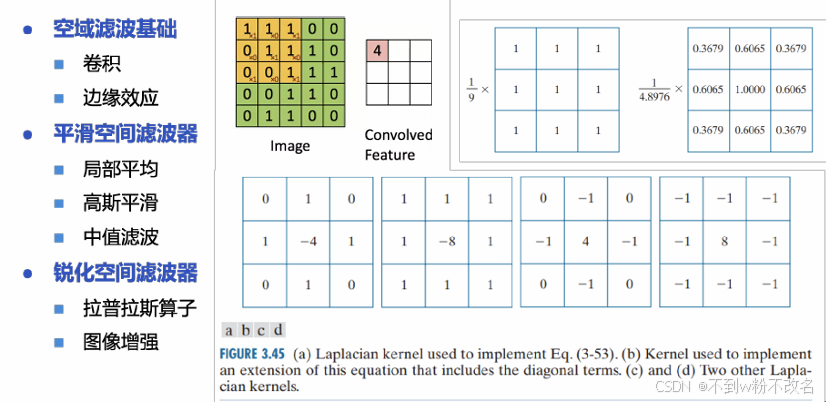
| 维度 | 平滑滤波 | 锐化滤波 |
|---|---|---|
| 数学本质 | 邻域加权平均(积分操作) | 梯度计算(微分操作) |
| 频域特性 | 低通滤波器(抑制高频,保留低频) | 高通滤波器(抑制低频,保留高频) |
| 对噪声的影响 | 减少噪声(但可能模糊细节) | 放大噪声(因噪声多为高频成分) |
| 边缘处理 | 弱化边缘,使边缘过渡平滑 | 强化边缘,使边缘更陡峭 |
| 典型算子示例 | 均值、高斯、中值 | 拉普拉斯、Sobel、非锐化掩模 |
| 视觉效果 | 图像变模糊,噪声减少 | 图像变清晰,细节更突出 |
选择策略:何时用平滑?何时用锐化?
1. 优先使用平滑滤波的场景
- 图像存在明显噪声(如拍摄时的 ISO 过高导致的噪点)。
- 需要去除小尺度纹理(如背景虚化),突出主体。
- 预处理步骤中需要降低图像分辨率(先平滑再缩放可减少锯齿)。
2. 优先使用锐化滤波的场景
- 图像因对焦不准或运动模糊导致细节模糊。
- 需要从图像中提取边缘特征(如物体识别、OCR 文字识别)。
- 增强图像的视觉冲击力(如广告图片中的产品细节强化)。
3. 组合使用案例
- 去噪 + 锐化流程:先中值滤波去除椒盐噪声,再用非锐化掩模恢复细节(如天文图像处理)。
- 保边处理:双边滤波(平滑噪声)+ 拉普拉斯锐化(增强保留的边缘),用于医学图像的器官分割前处理。
五、技术深层解析:为什么这些滤波器能实现对应效果?
1. 平滑滤波的数学原理
- 均值滤波 :通过邻域平均降低像素值方差,公式表达为:
邻域噪声通常是随机高频信号,平均后被弱化。
- 高斯滤波:权重符合高斯分布,离中心越近的像素影响越大,等效于对不同频率成分按高斯函数衰减,数学上可证明高斯滤波是唯一的 "各向同性" 平滑操作(无方向偏好)。
2. 锐化滤波的数学原理
- 一阶导数(梯度) :边缘处灰度值突变,梯度幅值大,因此梯度算子可定位边缘位置,如 Sobel 算子通过横向和纵向模板分别计算梯度:
- 二阶导数(拉普拉斯) :边缘处二阶导数为零,通过检测过零点可更精确地定位边缘,同时拉普拉斯算子的输出与原图叠加时,会在边缘处产生 "过冲" 和 "下冲",增强视觉对比度:
六、总结:平滑与锐化的辩证关系
- 互补性:平滑和锐化是图像处理中的 "对立统一"------ 平滑去除不必要的高频(噪声),锐化增强需要的高频(边缘)。
- 应用关键 :根据噪声类型和目标特征选择滤波器,例如:
- 高斯噪声→高斯滤波(线性平滑);
- 椒盐噪声→中值滤波(非线性平滑);
- 弱边缘目标→拉普拉斯锐化(二阶导数增强);
- 强边缘目标→Sobel 梯度(一阶导数定位)。
实际应用中常结合两者,如 "先平滑去噪,再适度锐化恢复细节",或通过参数调整(如高斯滤波的 σ、锐化的权重 k)平衡去噪与细节保留。
五、题目
1、下面的滤波器哪些可作为图像平滑滤波器,哪些可作为图像锐化滤波器?为什么?
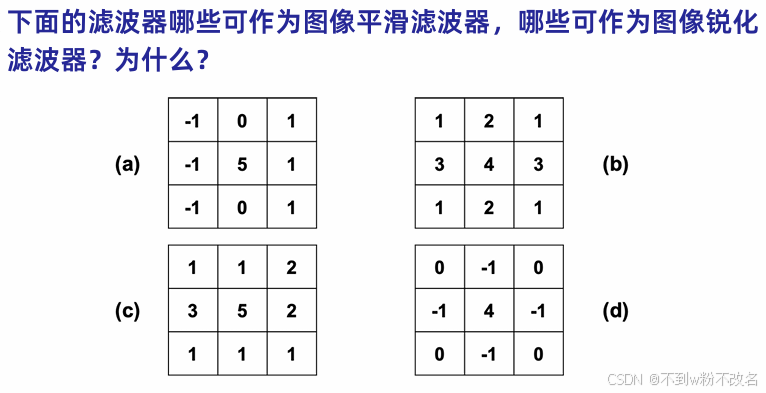
平滑滤波器(低通滤波)特点
数值均匀:所有值相近(如均值滤波器);
无正负交替:通常全为正数,中心值一般较大,邻近值较小且正。正数为平滑的必要条件。
锐化滤波器(高通滤波)特点
正负交替:通过正负值相乘增强边缘对比(例如,边缘像素与背景的差异被放大);
中心权重高:突出当前像素与邻域的差异,邻域像素为负或较小正数。
解:




2、问题1+问题2
问题1:以下两个滤波器属于平滑滤波器还是锐化滤波器?为什么?
都是平滑,都是正数,总和>9,模糊效果明显
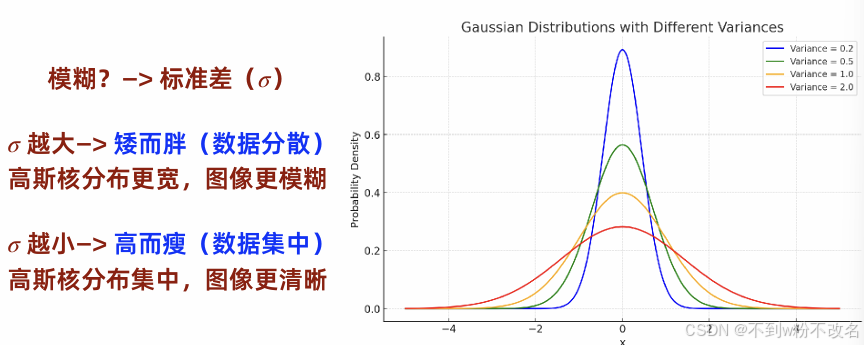
问题2:下面2个高斯滤波器对图像平滑,哪个滤波器使图像平滑后更模糊?为什么?
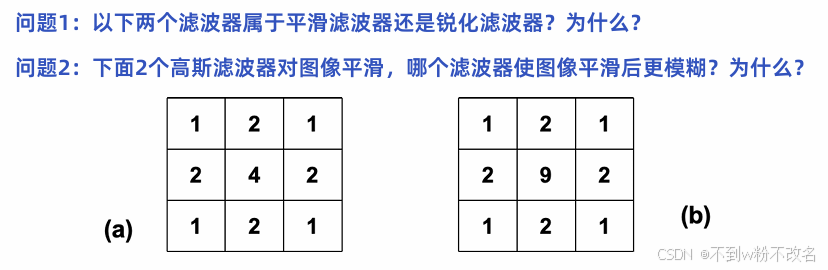
σ越大->高斯核分布更宽,图像模糊+
σ越小->高斯核分布集中,图像模糊 -
观察法(定性分析)
(a)中央元素为4,整体权重之和为:1+2+1+2+4+2+1+2+1=16
(b)中央元素为9,整体权重之和为:1+2+1+2+9+2+1+2+1=21
【中央值9相对于周围值占比更大,意味着它更倾向于保留当前像素本身的信息,对邻域的平滑作用较弱。 】
计算法(定量分析):通过离散统计方差估算标准差
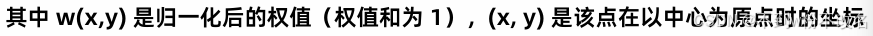
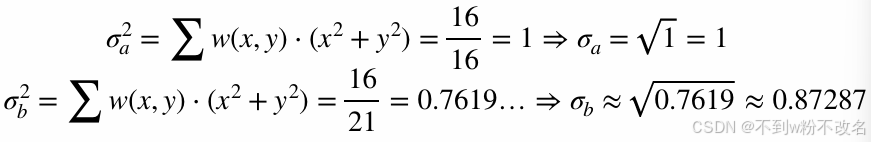
a更模糊,原因见上分析