在学习 StreetGS 代码中发现了其中的 Densification 策略与原 3DGS 不太一样,其是使用的 Gaussian Opacity Fields 中的一个的策略
我们先来回忆一下 3DGS 中一个比较重要 contribution:自适应密度控制
1 自适应密度控制
其具体步骤如下:
-
计算
xyz_gradient_accum和denom的比值,得到每个点的平均梯度grads -
densify_and_clone克隆:
-
筛选出梯度大于等于阈值的点。再进一步筛选出这些点中尺度小于等于场景范围的点。
-
直接复制一个添加即可(xyz不需要改变 ------ 之后训练会优化)
-
-
densify_and_split分裂: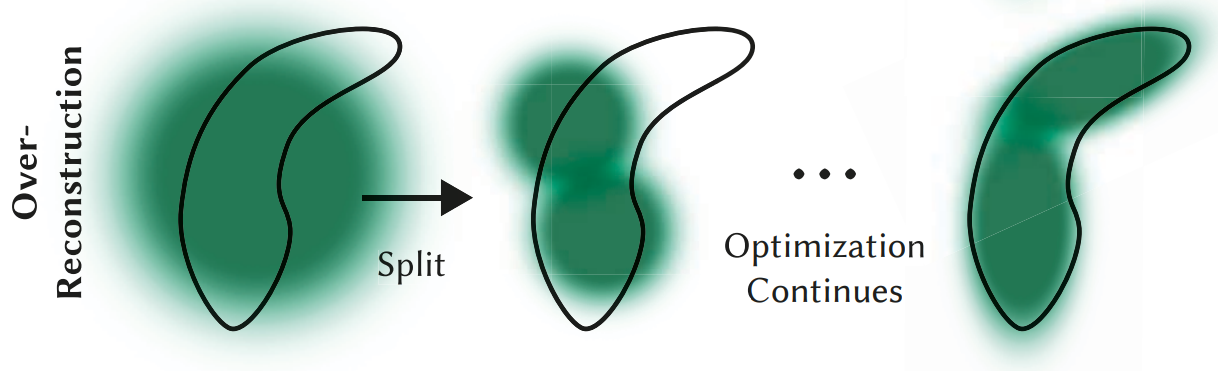
- 筛选出梯度大于等于阈值的点。再进一步筛选出这些点中尺度大于等于场景范围的点。
- 标准差
stds复制原来的值,均值means设为0(位置在原点)。生成新的samples。旋转矩阵也是原来的 - 计算新的位置
new_xyz:紧挨原本的点 - 计算新的缩放
new_scaling:两个点都同时除以1.6使变小 - 旋转、SH、不透明度、语义信息都复制即可
- 删除中间变量点(缩放前的两个大点)
-
修剪低不透明度的点和巨大点
-
重置
xyz_gradient_accum、denom和max_radii2D
可以看到计算 xyz_gradient_accum 和 denom 的比值,得到每个点的平均梯度 grads 是 clone 和 split 的第一个指标,其是拿来判断当前点是否拟合的较好的,高于一个阈值就说明当前这个点的梯度太大,拟合较差,需要进行优化,然后进一步判断是否进行 clone / split
2 绝对梯度策略
2.1 原 3DGS 策略
致密化是通过观察某个高斯函数的中心位置在视图空间中的变化梯度来进行的。这个变化梯度是通过分析该高斯对像素的贡献来计算的。
数学上,梯度 d L d x \frac{dL}{d\mathbf{x}} dxdL 对应的是目标函数相对于高斯中心 x \mathbf{x} x 的变化率。为了计算这个梯度,需要对高斯函数影响的所有像素 p i \mathbf{p}_i pi 进行求和。
M o l d = ∥ d L d x ∥ 2 = ∥ ∑ i d L d p i ⋅ d p i d x ∥ 2 M_{old} = \|\frac{dL}{d\mathbf{x}}\|_2 = \|\sum_i \frac{dL}{d\mathbf{p}_i} \cdot \frac{d\mathbf{p}_i}{d\mathbf{x}}\|_2 Mold=∥dxdL∥2=∥i∑dpidL⋅dxdpi∥2
------ 对应就是mean2D的梯度的前两维的L2范数
其中, p i \mathbf{p}_i pi 是像素, d L d p i \frac{dL}{d\mathbf{p}_i} dpidL 是目标函数对每个像素的梯度, d p i d x \frac{d\mathbf{p}_i}{d\mathbf{x}} dxdpi 是像素位置相对于高斯中心位置的梯度。
如果计算出的梯度范数 ∥ d L d x ∥ 2 \|\frac{dL}{d\mathbf{x}}\|2 ∥dxdL∥2 超过预设的阈值 τ x \tau{\mathbf{x}} τx,则该高斯函数会被选为致密化的候选对象。这意味着它可能处于一个需要增加更多点来更好描述的区域。
2.2 改进后策略
然而,Gaussian Opacity Fields 中作者发现上述度量并不能有效识别过度模糊的区域 。这是因为在某些情况下,不同像素的梯度信号可能会相互抵消,从而导致总的梯度大小较小,尽管该区域的重建质量实际上较差。
为了解决这个问题,作者提出了一种简单的改进方法,即直接累积每个像素梯度的范数,而不是计算总的梯度大小。这种做法可以更好地反映每个像素的重建误差,并避免梯度相互抵消的情况。
改进后的度量方式:
M n e w = ∑ i ∥ d L d p i ⋅ d p i d x ∥ M_{new} = \sum_i \left\|\frac{dL}{d\mathbf{p}_i} \cdot \frac{d\mathbf{p}_i}{d\mathbf{x}}\right\| Mnew=i∑ dpidL⋅dxdpi
------ 对应就是mean2D的梯度的最后一维,各个像素梯度的范数之和(CUDA代码是这样写的)
通过这种修改,新的度量标准 M n e w M_{new} Mnew 能更有效地识别出那些存在显著重建误差的区域,从而带来更好的场景重建和视图合成效果。
3 具体实现
这里的第一行就是原 3DGS 的 add_densification_stats 中累计梯度的操作,而第二行就是保存新的度量的操作,即直接保存 mean2D 的梯度的最后一维(CUDA代码中是有实现在最后一维保存各个像素梯度的范数之和)
python
model.xyz_gradient_accum[visibility_model, 0:1] += torch.norm(viewspace_point_tensor_grad_model[visibility_model, :2], dim=-1, keepdim=True)
model.xyz_gradient_accum[visibility_model, 1:2] += torch.norm(viewspace_point_tensor_grad_model[visibility_model, 2:], dim=-1, keepdim=True)这样,xyz_gradient_accum 的第一维就是以前的度量 M o l d M_{old} Mold ,第二维就是新的度量 M n e w M_{new} Mnew
在 densify_and_prune 中如果用绝对梯度策略就用第二维的 M n e w M_{new} Mnew 即可:
python
if cfg.optim.get('densify_grad_abs_bkgd', False):
grads = self.xyz_gradient_accum[:, 1:2] / self.denom
else:
grads = self.xyz_gradient_accum[:, 0:1] / self.denom在使用绝对梯度策略之后,可以明显看出绝对梯度比原梯度要大,每次 Densification 的点的数量相比较以前也大大增加:

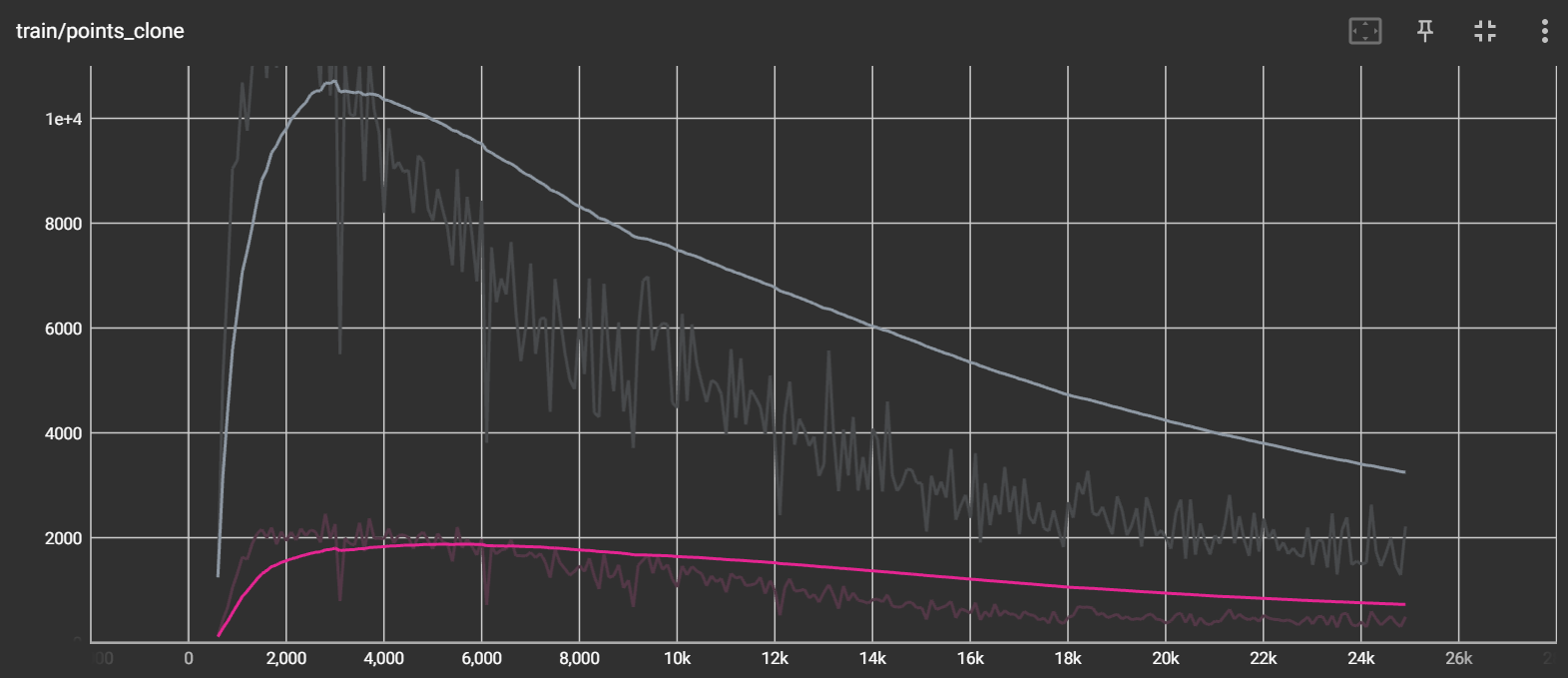
如上图可以看到,灰色即启用了绝对梯度策略的 clone 和 split,红线即没有启用的情况,两者差别还是挺大的