题目:
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在**原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
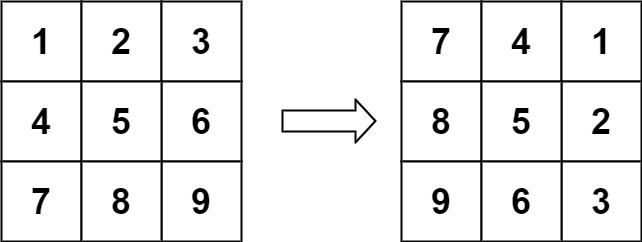
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
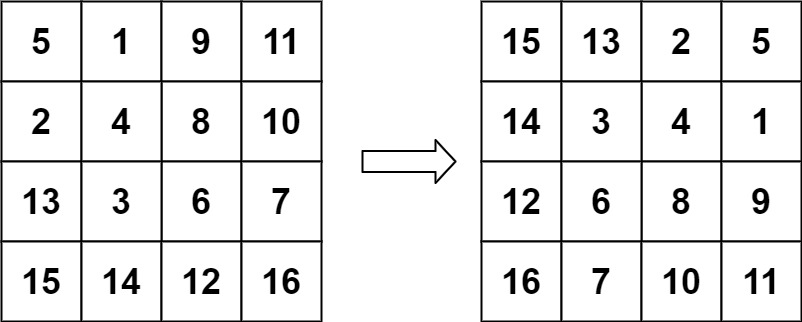
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]提示:
-
n == matrix.length == matrix[i].length -
1 <= n <= 20 -
-1000 <= matrix[i][j] <= 1000
步骤 1:问题分析
题目要求:
我们需要将一个 n × n 的二维矩阵(图像)顺时针旋转 90 度,且要求在原地进行操作。这意味着我们需要在输入矩阵本身上修改,不允许借助额外的矩阵存储。
输入输出条件:
- 输入 :一个二维矩阵
matrix,大小为 n × n ,其中1 <= n <= 20,且矩阵中每个元素的值在-1000到1000之间。 - 输出 :直接修改
matrix,使其成为顺时针旋转 90 度的结果。
约束与边界条件:
- 矩阵的大小 :n 的范围较小(最大为 20),因此在时间复杂度和空间复杂度上我们有一定的灵活性,可以考虑在 O(n\^2) 以内的算法。
- 原地旋转 :必须直接修改
matrix,不能借助另一个矩阵存储中间状态。
步骤 2:解题思路
目标描述:
顺时针旋转 90 度后的矩阵元素 (i, j) 会移动到新的位置 (j, n - i - 1)。为实现这一转换,我们可以分解成以下两步:
- 矩阵转置 :即将矩阵的行转换为列。此时
matrix[i][j]变为matrix[j][i]。 - 水平翻转:将转置后的每一行元素反转,从而完成 90 度旋转。
具体步骤解析:
- 矩阵转置 :
- 交换矩阵中
(i, j)和(j, i)位置的元素。 - 只需要遍历矩阵的上三角区域(即满足
i < j的位置),这样可以避免重复交换。
- 交换矩阵中
- 水平翻转 :
- 遍历矩阵的每一行,将每一行的元素进行对称交换(即
matrix[i][j]和matrix[i][n - j - 1]互换)。
- 遍历矩阵的每一行,将每一行的元素进行对称交换(即
时间复杂度和空间复杂度:
- 时间复杂度:O(n\^2),因为我们需要遍历矩阵的所有元素。
- 空间复杂度:O(1),因为是原地修改,没有使用额外的空间。
这种方法在效率和空间使用上是最优的。
还有一种方法那就是利用螺旋矩阵提取出来的元素,然后在换一个边界循环填充回去.
法一:

法二:
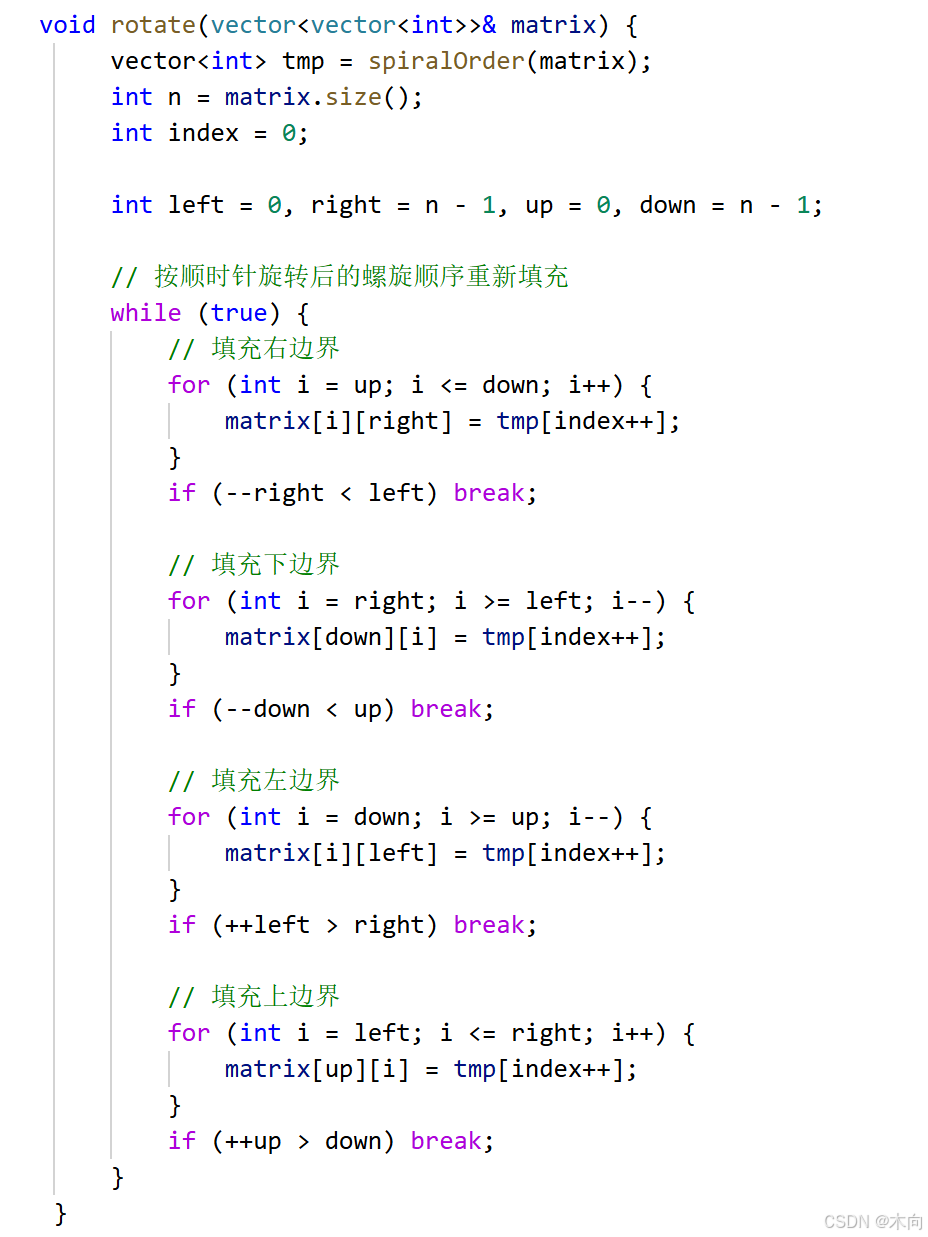
步骤 4:算法的启发与优化
法一展示了矩阵变换的分解思路 ,即通过分步操作(转置和水平翻转)来实现整体的旋转操作。这种方法避免了重复操作和多余的空间开销。针对二维矩阵的其他旋转操作(例如逆时针 90 度),可以类比这种分解方法,通过组合不同的操作(如转置和垂直翻转)来实现。
步骤 5:实际应用
应用场景
图像和视频处理领域经常需要对二维图像矩阵进行旋转、翻转等变换。顺时针旋转 90 度在图像旋转、照片编辑、游戏引擎开发、地图视角切换等方面都十分常见。
示例应用
在一个地理信息系统(GIS)中,地图显示需要根据用户的设备方位调整视角(比如将北方置于屏幕顶部)。假设地图数据以二维矩阵的形式存储,那么可以在后台使用该算法快速旋转视图,实现顺时针调整或适应不同的用户视角。具体实现时可以先根据角度选择旋转操作,再在应用中显示旋转后的数据,提升用户的交互体验。