导航
-
-
- [1.6 系统的Petri网模型](#1.6 系统的Petri网模型)
-
- [例 1.6 化学反应](#例 1.6 化学反应)
- [例 1.7 进程的通信协议](#例 1.7 进程的通信协议)
- [例 1.8 P/V操作](#例 1.8 P/V操作)
- [例 1.9 临界段互斥问题](#例 1.9 临界段互斥问题)
- [例 1.10 生产者/消费者问题](#例 1.10 生产者/消费者问题)
- [例 1.11 哲学家就餐问题](#例 1.11 哲学家就餐问题)
-
1.6 系统的Petri网模型
理论的目的在于应用,接下来是一些关于用Petri网标识离散事件系统的例子
这里就直接搬运书上的内容了,了解一下
例 1.6 化学反应
图 1.23 给出了一个含有 3 个库所 s 1 s_1 s1、 s 2 s_2 s2、 s 3 s_3 s3 和一个变迁 t t t 的加权 Petri 网,易知从图 1.23a) 的标识经过 t t t 的发生可以产生图 1.23b) 的标识。如果我们用库所 s 1 s_1 s1、 s 2 s_2 s2 和 s 3 s_3 s3 中的标志分别表示氢分子、氧分子和水分子的个数,变迁 t t t 表示化合反应,那么变迁 t t t 的发生和这个网中标识的变化反映了
2 H 2 + 2 O 2 → 2 H 2 O + O 2 2H_2 + 2O_2 \rightarrow 2H_2O + O_2 2H2+2O2→2H2O+O2
的化学反应过程。

例 1.7 进程的通信协议
图 1.24 是两个进程之间的通信协议的简化模型。进程 A A A 准备好的信息通过变迁 t 2 t_2 t2 的发生向进程 B B B 发送,先送到缓冲寄存器 s 4 s_4 s4。如果进程 B B B 做好接收信息的准备,便通过变迁 t 4 t_4 t4 的发生从 s 4 s_4 s4 中接收进程 A A A发送的信息,并通过变迁 t 5 t_5 t5 的发生向进程 A A A 发送应答,应答信息通过缓冲寄存器 s 5 s_5 s5 回送到进程 A A A。变迁 t 3 t_3 t3 是进程 A A A 接收应答的描述。当进程 A A A 发送信息(即 t 2 t_2 t2 发生)后,库所 s 3 s_3 s3 中有一个标志,表示进程 A A A 随时准备接收应答。以上过程可重复多次。
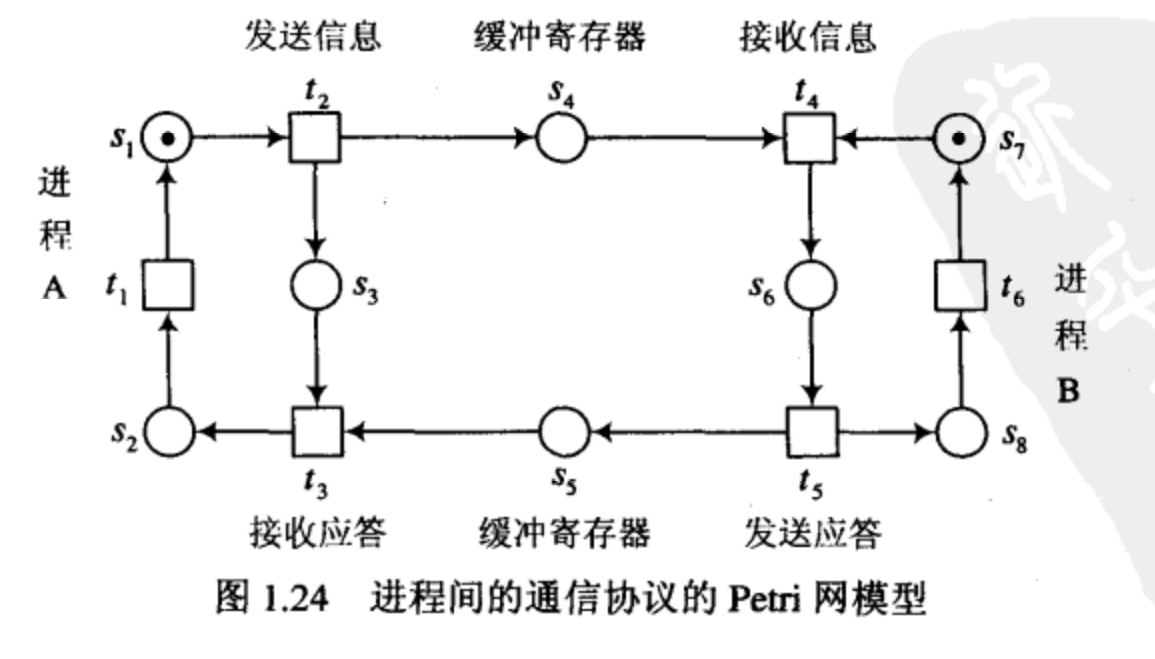
例 1.8 P/V操作
P/V 操作是操作系统中的一种基本操作,它们是定义在信号量(semaphore)上的。信号量是一个非负整数量,一个 V 操作使信号量的值加 1,而一个 P 操作使信号量的值减 1。由于要求信号量的值为非负,所以只有当信号量的值为正时,P 操作才能进行。信号量的 P/V 操作可以用图 1.25 的 Petri 网模型表示,其中库所 s s s 中的标志数量是信号量 S S S 的值。
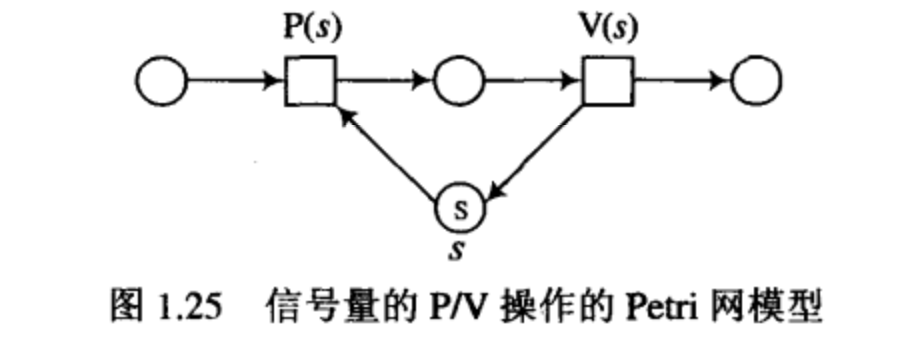
例 1.9 临界段互斥问题
在多个进程共享一个数据项的情况下,各个进程对数据项的最基本操作是读和写。然而,一个进程读到数据项的值后,通过计算可能修改数据项的值,然后写回原处。这便是对数据项进行更新。在这种情况下,另一个进程是使用这个数据项的原值还是使用更新后的值,结果是不一样的。如果要使用更新后的值,就应设置临界段,要求一个进程使用共享的数据项期间,另一个进程不能读取这个数据项。这就是所谓进程的互斥问题。这样的一个系统可以用图 1.26 的 Petri 网模型来描述。图中 s 4 s_{4} s4表示共享的数据项。
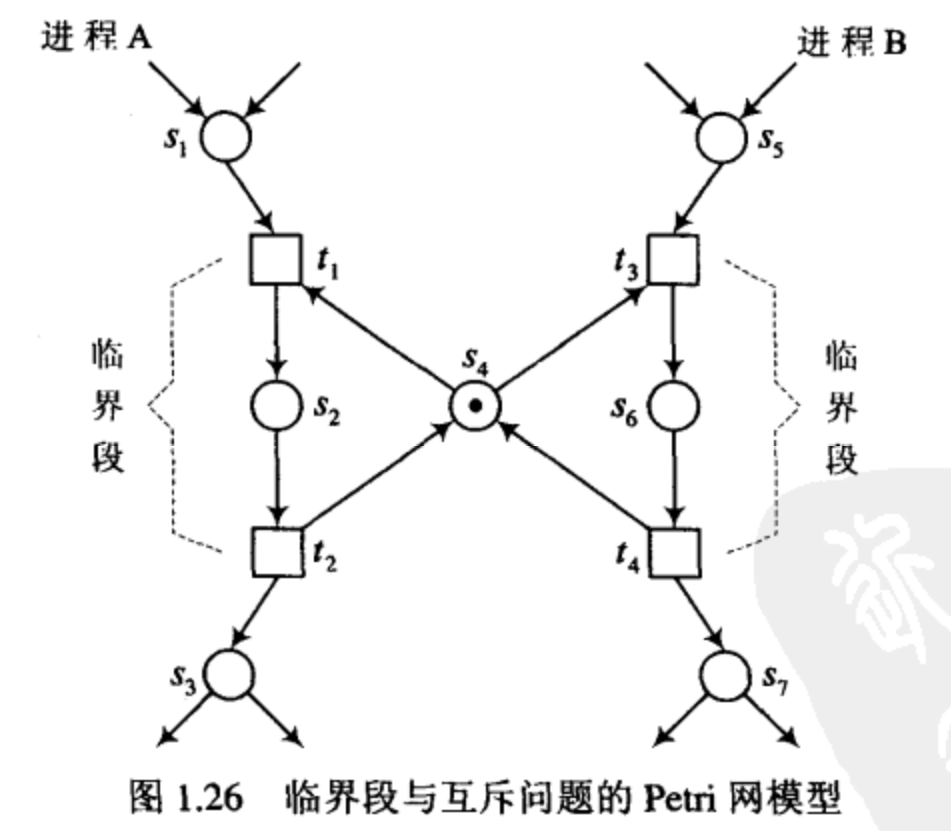
例 1.10 生产者/消费者问题
生产者/消费者系统属于另一类资源共享系统。生产者进程和消费者进程的共享资源是缓冲寄存器(buffer),不过缓冲寄存器对它们有不同的作用。生产者进程把生产出来的数据项存入缓冲寄存器,而消费者进程从缓冲寄存器中取走数据项,并消费它们。
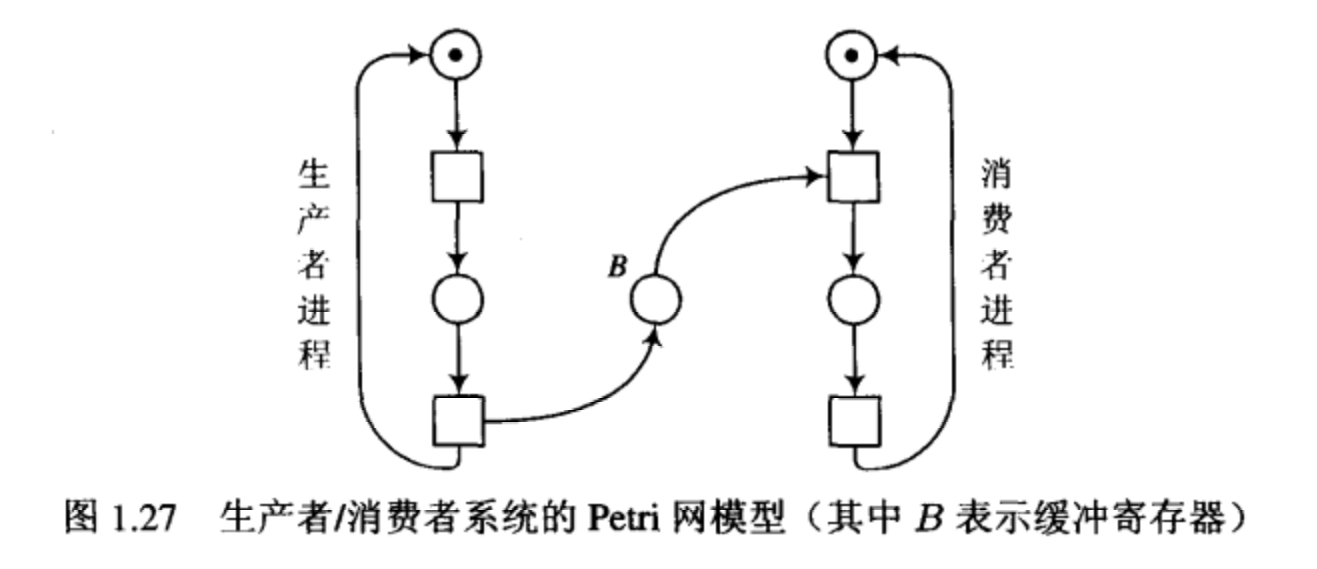
消费者进程能够运行的条件是缓冲寄存器中含有未被消费的数据项。而生产者进程能够运行的条件是缓冲寄存器不溢出,因为缓冲寄存器的容量一般是有限制的。生产者/消费者系统的 Petri 网模型如图 1.27 所示。
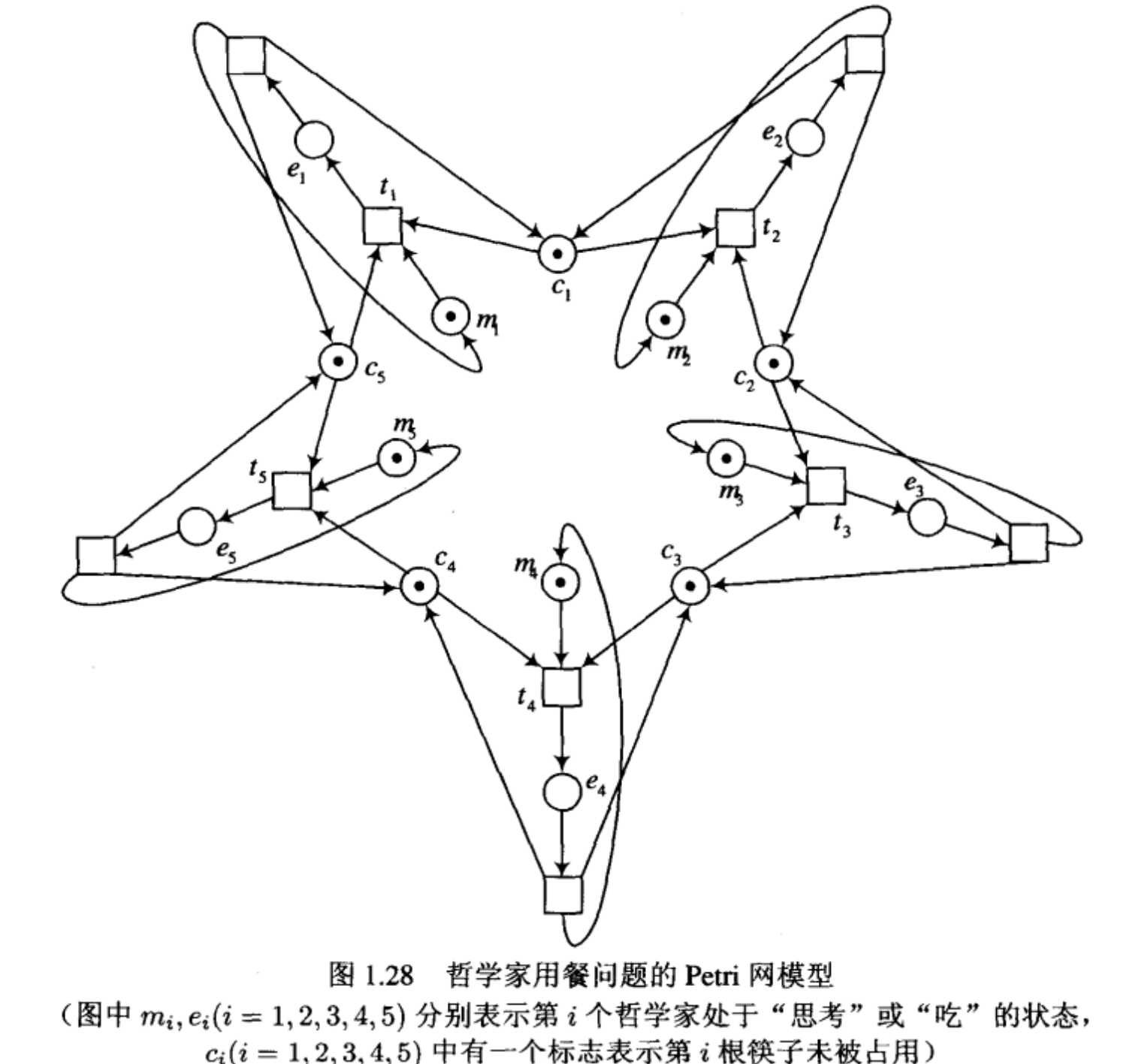
例 1.11 哲学家就餐问题
Dijkstra 提出的哲学家用餐问题是资源共享系统的一个通俗的典型例子。5个哲学家坐在一个圆桌旁,圆桌上摆满了中餐食品,每两个哲学家之间摆了一根筷子。一个哲学家要吃食品时,必须同时拿起他左边的和右边的筷子。这时坐在他旁边的两位哲学家就不可能有足够的筷子来吃食品,只能坐在那里思考问题。每位哲学家从"思考"状态进入"吃食品"状态的条件是在他左、右两边的两根筷子未被使用。图1.28 是这个问题的一个 Petri 网模型(引自参考文献[8])。这个模型已对问题进行了一定的处理:规定只有当一个哲学家身边的左右两根筷子都未被占用时,他才能拿起筷子(而且同时拿两根筷子)。这样才能避免这样一种情况:每位哲学家都拿起一根(譬如说右边的一根)筷子不放下,等待别人让步,而结果谁也吃不上。
比较复杂的建模问题,用高级Petri网建模
到此第一章完结撒花~~