从零开始机器学习——基于PyTorch构建你的第一个线性回归模型

bjxiaxueliang2024-10-28 11:39

随着人工智能技术的迅猛发展，机器学习成为了现代科技领域中最炙手可热的话题之一。然而，对于初学者来说，机器学习似乎总是充满了复杂的理论和难以理解的概念。本文将带你从零开始，使用PyTorch深度学习框架，构建一个最简单的线性回归模型，一步步揭开机器学习的神秘面纱。无需预先的专业背景知识，只需跟随本文的指导，你就能亲手实现一个可以预测数据的机器学习模型！

一、什么是线性回归

线性回归是一种最基本的监督学习方法，其试图找到输入特征与输出结果之间的线性关系。通过训练模型，我们可以学习到一组参数，使得模型能够预测新的未知数据。

二、构建线性模型

在本文中，我们将使用 Python 的 PyTorch 库来构建一个简单的线性回归模型。PyTorch 是一个强大的深度学习框架，它不仅支持动态计算图，还提供了大量的预定义模块和工具，使得机器学习变得更加容易。

2.1 数据准备

首先，我们需要准备一些训练数据。假设我们有三个样本点，每个样本有一个输入特征和一个对应的样本输出值：

python 复制代码 
# 数据准备：x_data 和 y_data 是两个张量（Tensor），分别代表"输入数据"和对应的"标签数据"。
# x_data 包含了数值 [1.0, 2.0, 3.0]，而 y_data 包含了 [2.0, 4.0, 6.0]，这表明 y_data 中的每个值都是对应 x_data 值的两倍。
# 我们的目标是训练一个模型，使其能够学习到这种输入与输出之间的映射关系。
x_data = torch.Tensor([[1.0], [2.0], [3.0]])  # 输入数据
y_data = torch.Tensor([[2.0], [4.0], [6.0]])  # 标签数据

这里，x_data 是输入特征，y_data 是样本输出值。

2.2 定义模型

接下来，我们需要定义一个模型来学习输入特征与输出值之间的关系。这里我们使用 PyTorch 提供的 torch.nn.Module 来定义一个简单的线性模型。

python 复制代码 
# 定义一个名为 LinearModel 的类，该类继承自 torch.nn.Module
class LinearModel(torch.nn.Module):
    # 在 __init__ 方法中，创建了一个线性层 self.linear = torch.nn.Linear(1, 1)，接受一个输入特征并产生一个输出特征
    def __init__(self):
        super(LinearModel, self).__init__()
        # 实例化了一个具有单个输入和单个输出的线性层。
        # 这意味着该层会学习一个权重和一个偏差值，用于将输入标量转换成输出标量。
        self.linear = torch.nn.Linear(1, 1)
    # 定义了如何通过模型进行前向传播。对于输入 x，它返回经过线性变换后的结果 y_pred。
    def forward(self, x): 
        y_pred = self.linear(x) 
        return y_pred

在这个模型中，我们创建了一个线性层，它将输入的标量值转换为一个标量输出。

2.3 损失函数和优化器

为了训练模型，我们需要定义损失函数和优化器。

  • 损失函数衡量了模型预测值与实际值之间的差异；
  • 优化器则负责根据损失函数的反馈来更新模型参数。
python 复制代码 
# 创建一个 LinearModel 类的实例
model = LinearModel()
# 均方误差损失函数：torch.nn.MSELoss 计算预测值和真实值之间的均方误差
# size_average=False 控制损失值是否会被平均
criterion = torch.nn.MSELoss(size_average=False)
# 随机梯度下降优化器：torch.optim.SGD 随机梯度下降优化器，通过沿着梯度方向更新参数来最小化损失函数。
# model.parameters() 获取模型的所有可学习参数。LinearModel 中定义了一个线性层，其有两个参数"权重weight"、"偏置bias"。model.parameters()返回这两个参数。
# lr=0.01 学习率（Learning Rate），决定了每次参数更新的步长大小。
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

2.4 训练模型

现在，我们可以开始训练模型了，通过多次迭代来调整模型参数，使其能够更好地拟合数据。

python 复制代码 
# 训练模型:
# 在 for 循环中迭代执行 1000 次训练周期（epoch）。每一次迭代中：
for epoch in range(1000):
    # 计算模型对 x_data 的预测 y_pred
    y_pred = model(x_data)
    # 计算损失 loss，即 y_pred 与实际标签 y_data 之间的差异
    loss = criterion(y_pred, y_data)
    # 打印当前的 epoch 数和损失值
    print(epoch, loss.item())
    # 清空梯度缓存：
    # 在PyTorch中，梯度是通过反向传播计算出来的。
    # 当我们调用 loss.backward() 时，PyTorch会自动计算损失函数关于模型参数的梯度，并将这些梯度存储在每个参数的.grad 属性中。
    # 如果不显式地清零梯度，那么每次调用loss.backward()都会将新计算出的梯度加上上次计算的结果，导致梯度不正确。
    optimizer.zero_grad()
    # 反向传播计算梯度
    loss.backward()
    # 在完成一次反向传播计算梯度之后，根据这些梯度更新模型的参数。利用优化器中定义的更新规则，来调整模型的权重和偏置，以期减少损失函数的值。
    optimizer.step()

在训练过程中，我们通过 loss.backward() 计算损失相对于模型参数的梯度，并通过 optimizer.step() 使用这些梯度来更新模型参数。

2.5 测试模型

训练完成后，我们可以查看模型学习到的权重和偏置，并用它来预测新的输入数据。

python 复制代码 
#
# 打印出模型的权重 model.linear.weight.item()
print('w = ', model.linear.weight.item())
# 打印出模型的偏置 model.linear.bias.item()
print('b = ', model.linear.bias.item())
#
# 使用训练好的模型预测新的输入 x_test = [[4.0]] 对应的输出值 y_test 并打印出来
x_test = torch.Tensor([[4.0]]) 
y_test = model(x_test) 
print('y_pred = ', y_test.data)

三、模型网络结构及源码

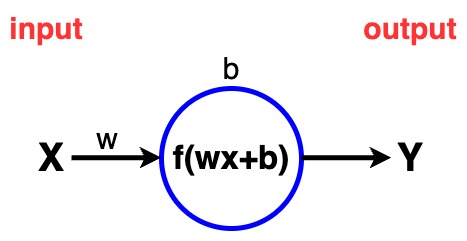
这个模型可以被视为最简单的线性回归模型，其结构可以用以下公式表示：

y = f ( w ∗ x + b ) y=f(w * x + b) y=f(w∗x+b)

其中：

  • x 是输入数据；
  • y 是预测输出；
  • w 是权重；
  • b 是偏置项；
  • f是激活函数：由于该模型为一个非常简单的线性回归模型，只包含一个线性层，代码实现中并没有使用激活函数，但还是有必要了解一下激活函数，所以这里将其写了出来。
    激活函数的作用是将那些无边界的输入转化成一组良好的，可预测的输出形式。一种常用的激活函数是Sigmoid函数，该激活函数仅输出范围(0,1)之间的数，你可以把它想象成将一组存在于(−∞,+∞)间的数字压缩到(0,1)之间，越大的负数（指绝对值越大）输出后会越接近0，越大的正数输出后会越接近1。

3.1 模型网络结构

其模型网络结构也是非常简单，只有一个网络节点。

3.2 完整源代码

在模型训练过程中，模型通过不断调整权重 w 和偏置 b 来最小化损失函数（均方误差），使得模型的预测值 y_pred 尽可能接近实际标签 y_data。

最终完整的可执行源代码如下：

python 复制代码 
# 案例详细展示了如何使用 PyTorch 框架，从零开始构建一个单输入单输出的线性回归模型。
# 然后通过梯度下降法对模型进行训练，以预测输入值对应的输出值。
# 以下是详细的步骤解析说明：
import torch
# 数据准备：x_data 和 y_data 是两个张量（Tensor），分别代表"输入数据"和对应的"标签数据"。
# x_data 包含了数值 [1.0, 2.0, 3.0]，而 y_data 包含了 [2.0, 4.0, 6.0]，这表明 y_data 中的每个值都是对应 x_data 值的两倍。
# 因此，我们的目标是训练一个模型，使其能够学习到这种输入与输出之间的映射关系。
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])

# 定义一个名为 LinearModel 的类，该类继承自 torch.nn.Module
class LinearModel(torch.nn.Module):
    # 在 __init__ 方法中，创建了一个线性层 self.linear = torch.nn.Linear(1, 1)，接受一个输入特征并产生一个输出特征
    def __init__(self):
        super(LinearModel, self).__init__()
        # 实例化了一个具有单个输入和单个输出的线性层。
        # 这意味着该层会学习一个权重和一个偏差值，用于将输入标量转换成输出标量。
        self.linear = torch.nn.Linear(1, 1)
    # 定义了如何通过模型进行前向传播。对于输入 x，它返回经过线性变换后的结果 y_pred。
    def forward(self, x): 
        y_pred = self.linear(x) 
        return y_pred

# 创建一个 LinearModel 类的实例
model = LinearModel()
# 均方误差损失函数：torch.nn.MSELoss 计算预测值和真实值之间的均方误差
# size_average=False 控制损失值是否会被平均
criterion = torch.nn.MSELoss(size_average=False)
# 随机梯度下降优化器：torch.optim.SGD 随机梯度下降优化器，通过沿着梯度方向更新参数来最小化损失函数。
# model.parameters() 获取模型的所有可学习参数。LinearModel 中定义了一个线性层，其有两个参数"权重weight"、"偏置bias"。model.parameters()返回这两个参数。
# lr=0.01 学习率（Learning Rate），决定了每次参数更新的步长大小。
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
#
# 训练模型:
# 在 for 循环中迭代执行 1000 次训练周期（epoch）
for epoch in range(1000):
    # 计算模型对 x_data 的预测 y_pred
    y_pred = model(x_data)
    # 计算损失 loss，即 y_pred 与实际标签 y_data 之间的差异
    loss = criterion(y_pred, y_data)
    # 打印当前的 epoch 数和损失值
    print(epoch, loss.item())
    # 清空梯度缓存：
    # 在PyTorch中，梯度是通过反向传播计算出来的。
    # 当我们调用 loss.backward() 时，PyTorch会自动计算损失函数关于模型参数的梯度，并将这些梯度存储在每个参数的.grad 属性中。
    # 如果不显式地清零梯度，那么每次调用loss.backward()都会将新计算出的梯度加上上次计算的结果，导致梯度不正确。
    optimizer.zero_grad()
    # 反向传播计算梯度
    loss.backward()
    # 在完成一次反向传播计算梯度之后，根据这些梯度更新模型的参数。利用优化器中定义的更新规则，来调整模型的权重和偏置，以期减少损失函数的值。
    optimizer.step()
#
# 打印出模型的权重 model.linear.weight.item()
print('w = ', model.linear.weight.item())
# 打印出模型的偏置 model.linear.bias.item()
print('b = ', model.linear.bias.item())
#
# 使用训练好的模型预测新的输入 x_test = [[4.0]] 对应的输出值 y_test 并打印出来
x_test = torch.Tensor([[4.0]]) 
y_test = model(x_test) 
print('y_pred = ', y_test.data)

3.3 训练参数及预测结果

模型的训练参数及预测结果输出：

java 复制代码 
w =  1.9996986389160156
b =  0.0006850397912785411
y_pred =  tensor([[7.9995]])

这个模型是一个非常基础的单输入单输出线性回归模型，适用于解决简单的回归问题，例如预测输入标量与输出标量之间的线性关系。尽管模型结构简单，但它为我们提供了一个很好的起点，以了解如何使用 PyTorch 构建和训练模型。

四、增加模型节点

要增加模型的节点，即增加隐藏层或增加隐藏层中的节点数，可以通过修改模型定义来实现。以下是增加隐藏层数和增加隐藏层节点数的示例。

4.1 增加隐藏层数

如果我们想增加隐藏层数，可以在模型中添加隐藏层。例如，增加一个隐藏层。

python 复制代码 
# 定义带有隐藏层的线性模型  
class MultiLayerLinearModel(torch.nn.Module):  
    def __init__(self):  
        super(MultiLayerLinearModel, self).__init__()  
        # 添加一个隐藏层，输入1个特征，输出1个特征  
        self.hidden = torch.nn.Linear(1, 1)  
        # 添加一个输出层，输入1个特征，输出1个特征  
        self.output = torch.nn.Linear(1, 1)  
  
    def forward(self, x):  
        # 通过隐藏层，激活函数可以使用ReLU或其他激活函数  
        x = torch.relu(self.hidden(x))  
        # 通过输出层  
        y_pred = self.output(x)  
        return y_pred

4.2 增加隐藏层数

如果我们想增加隐藏层的节点数，可以修改隐藏层的输入和输出特征数。例如，将隐藏层的输出特征数从 1 增加到 3。

python 复制代码 
# 定义一个名为 LinearModel 的类，该类继承自 torch.nn.Module  
class MultiLayerLinearModel(torch.nn.Module):  
    def __init__(self):  
        super(MultiLayerLinearModel, self).__init__()  
        # 添加一个隐藏层，输入1个特征，输出3个特征  
        self.hidden = torch.nn.Linear(1, 3)  
        # 添加一个输出层，输入3个特征，输出1个特征  
        self.output = torch.nn.Linear(3, 1)  
  
    def forward(self, x):  
        # 通过隐藏层，激活函数可以使用ReLU或其他激活函数  
        x = torch.relu(self.hidden(x))  
        # 通过输出层  
        y_pred = self.output(x)  
        return y_pred

4.3 完整代码

以下是完整的代码示例，包括增加隐藏层节点数和增加隐藏层数的情况：

python 复制代码 
import torch  
  
# 数据准备：x_data 和 y_data 是两个张量（Tensor），分别代表"输入数据"和对应的"标签数据"。  
# x_data 包含了数值 [1.0, 2.0, 3.0]，而 y_data 包含了 [2.0, 4.0, 6.0]，这表明 y_data 中的每个值都是对应 x_data 值的两倍。  
# 因此，我们的目标是训练一个模型，使其能够学习到这种输入与输出之间的映射关系。  
x_data = torch.Tensor([[1.0], [2.0], [3.0]])  
y_data = torch.Tensor([[2.0], [4.0], [6.0]])  
#  
# 定义一个名为 LinearModel 的类，该类继承自 torch.nn.Module  
class MultiLayerLinearModel(torch.nn.Module):  
    def __init__(self):  
        super(MultiLayerLinearModel, self).__init__()  
        # 添加一个隐藏层，输入1个特征，输出3个特征  
        self.hidden = torch.nn.Linear(1, 3)  
        # 添加一个输出层，输入3个特征，输出1个特征  
        self.output = torch.nn.Linear(3, 1)  
  
    # 定义了如何通过模型进行前向传播。  
    def forward(self, x):  
        # 通过隐藏层，激活函数可以使用ReLU或其他激活函数  
        x = torch.relu(self.hidden(x))  
        # 通过输出层  
        y_pred = self.output(x)  
        return y_pred  
  
#  
# 创建一个 MultiLayerLinearModel 类的实例  
model = MultiLayerLinearModel()  
# 均方误差损失函数：torch.nn.MSELoss 计算预测值和真实值之间的均方误差  
# size_average=False 控制损失值是否会被平均  
criterion = torch.nn.MSELoss(size_average=False)  
# 随机梯度下降优化器：torch.optim.SGD 随机梯度下降优化器，通过沿着梯度方向更新参数来最小化损失函数。  
# model.parameters() 获取模型的所有可学习参数。LinearModel 中定义了一个线性层，其有两个参数"权重weight"、"偏置bias"。model.parameters()返回这两个参数。  
# lr=0.01 学习率（Learning Rate），决定了每次参数更新的步长大小。  
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  
#  
# 训练模型:  
# 在 for 循环中迭代执行 1000 次训练周期（epoch）  
for epoch in range(1000):  
    # 计算模型对 x_data 的预测 y_pred  
    y_pred = model(x_data)  
    # 计算损失 loss，即 y_pred 与实际标签 y_data 之间的差异  
    loss = criterion(y_pred, y_data)  
    # 打印当前的 epoch 数和损失值  
    print(epoch, loss.item())  
    # 清空梯度缓存：  
    # 在PyTorch中，梯度是通过反向传播计算出来的。    # 当我们调用 loss.backward() 时，PyTorch会自动计算损失函数关于模型参数的梯度，并将这些梯度存储在每个参数的.grad 属性中。    # 如果不显式地清零梯度，那么每次调用loss.backward()都会将新计算出的梯度加上上次计算的结果，导致梯度不正确。    optimizer.zero_grad()  
    # 反向传播计算梯度  
    loss.backward()  
    # 在完成一次反向传播计算梯度之后，根据这些梯度更新模型的参数。利用优化器中定义的更新规则，来调整模型的权重和偏置，以期减少损失函数的值。  
    optimizer.step()  
#  
# 打印模型参数  
print('Hidden layer：')  
print('w = ', model.hidden.weight)  
print('b = ', model.hidden.bias)  
print('Output layer：')  
print('w = ', model.output.weight)  
print('b = ', model.output.bias)  
  
# 测试模型  
x_test = torch.Tensor([[4.0]])  
y_test = model(x_test)  
print('y_pred = ', y_test.data)

4.4 训练参数及预测结果

模型的训练参数及预测结果输出：

java 复制代码 
Hidden layer：
w =  Parameter containing:tensor([[0.1732],[1.4368],[-0.9307]], requires_grad=True)
b =  Parameter containing:tensor([ 0.0400, -0.1946,  0.5237], requires_grad=True)
Output layer：
w =  Parameter containing:tensor([[0.0159, 1.3901, 0.5729]], requires_grad=True)
b =  Parameter containing:tensor([0.2699], requires_grad=True)
y_pred =  tensor([[8.0000]])

4.5 模型网络结构

增加隐藏层和增加隐藏层中的节点数后的模型网络结构如下图所示。

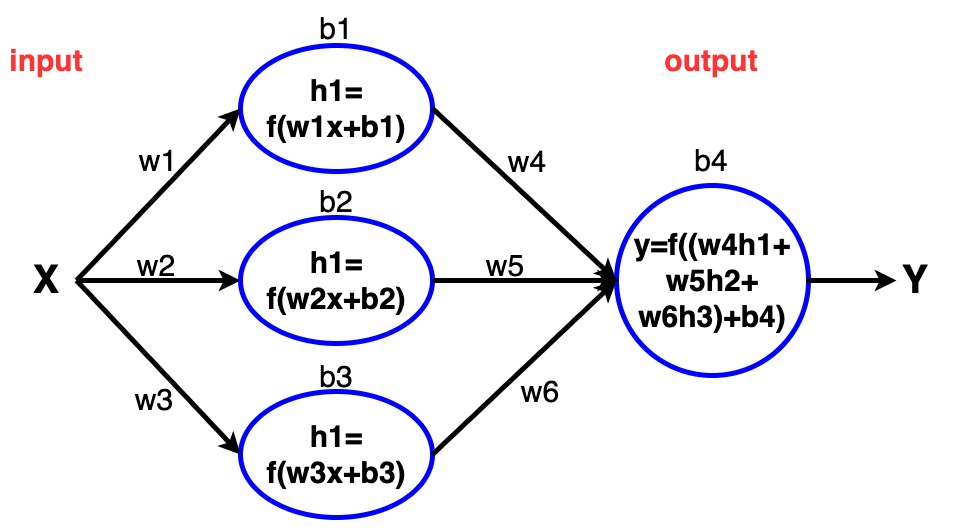
注：
f是激活函数，激活函数用来将那些无边界的输入转化成一组良好的，可预测的输出形式。一种常用的激活函数是Sigmoid函数，该激活函数仅输出范围(0,1)之间的数，你可以把它想象成将一组存在于(−∞,+∞)间的数字压缩到(0,1)之间，越大的负数（指绝对值越大）输出后会越接近0，越大的正数输出后会越接近1。

五、参考

An Introduction to Neural Networks
https://victorzhou.com/blog/intro-to-neural-networks/

PyTorch简单示例：
https://blog.csdn.net/yj13811596648/article/details/106886666

相关推荐
铁盒薄荷糖1 小时前
【Pytorch】Pytorch的安装
人工智能·pytorch·python
yyfhq1 小时前
rescorediff
python·深度学习·机器学习
思通数据1 小时前
AI助力医疗数据自动化：诊断报告识别与管理
大数据·人工智能·目标检测·机器学习·计算机视觉·目标跟踪·自动化
(●'◡'●)知1 小时前
基于树莓派的安保巡逻机器人--（一、快速人脸录入与精准人脸识别）
人工智能·python·opencv·机器学习·计算机视觉
迷路爸爸1803 小时前
深入理解Allan方差：用体重数据分析误差的时间尺度与稳定性
机器学习·数据分析·概率论
Kalika0-04 小时前
多层感知机从零开始实现
pytorch·学习
T0uken4 小时前
【机器学习】过拟合与欠拟合
人工智能·机器学习
机器学习之心5 小时前
GCN+BiLSTM多特征输入时间序列预测（Pytorch）
人工智能·pytorch·python·gcn+bilstm
qiaoxinyu19896 小时前
线性代数（1）——线性方程组的几何意义
线性代数·算法·机器学习
热门推荐
01Windows10安装PCL1.14.0及点云配准02组基轨迹建模 GBTM的介绍与实现（Stata 或 R）03【经验分享】Ubuntu22.04安装微信(linux官方版)04前端vue3实现本地及在线文件预览（含pdf/txt/mp3/mp4/docx/xlsx/pptx）05制冷毛细管的计算方法介绍06RAG 实践- Ollama+RagFlow 部署本地知识库07ECharts 地图实战分析：实现一个完整的地图下钻功能08Coze扣子平台完整体验和实践（附国内和国际版对比）09苍穹外卖面试总结10基于YOLOv10深度学习的CT扫描图像肾结石智能检测系统【python源码+Pyqt5界面+数据集+训练代码】深度学习实战、目标检测