dp(完全,线性,树状,状压,数位)>= 搜索 == 基础算法(二分,前缀和,高精度,公约数,公倍数,质数,排序) > 数据结构(树的构造,树的遍历,公共祖先,链表,树状数组,队列) > 图论(并查集,diji,floyd,prim,拓扑) ≈ 数论
C++ 头文件
数据流输入/输出:cin>>,cout<<的头文件:#include
c语言输入流:#include <stdio.h>
算法类函数:sort()...的头文件 #include
各个数学函数:max(),min(),sqrt()...的头文件 #include <math.h> 或 #include
字符串操作的头文件 #include 或 #include
结构类的头文件:
链表 #include
图 #include
队列 #include
迭代器 #include
栈 #include
闰年:两个条件均可(能被4整除不能被100整除)(能被400整除)
动态规划
题单:
目录
背包问题
背包问题初始化总结
AcWing 2. 01背包问题
AcWing 3. 完全背包问题
AcWing 4. 多重背包问题
AcWing 5. 多重背包问题 II
AcWing 9. 分组背包问题
线性DP
AcWing 898. 数字三角形
AcWing 895. 最长上升子序列
AcWing 896. 最长上升子序列 II(贪心)
AcWing 897. 最长公共子序列
AcWing 902. 最短编辑距离
AcWing 899. 编辑距离
区间DP
AcWing 282. 石子合并(m i n minmin)
计数类DP
AcWing 900. 整数划分(完全背包求方案数,体积恰好)
数位统计DP
AcWing 338. 计数问题
状态压缩DP
AcWing 291. 蒙德里安的梦想
AcWing 91. 最短Hamilton路径
树形DP
AcWing 285. 没有上司的舞会
记忆化搜索
AcWing 901. 滑雪
一.从记忆化搜索到递推
启发思路:选或不选---》状态转移方程
dp三步走:
- 思考回溯写法
- 改成记忆化搜索
- 1:1翻译成递推
举例:打家劫舍
1.思考回溯写法
dfs(i,nums):意味着找前i个数的最大和
对于第i个数选还是不选,
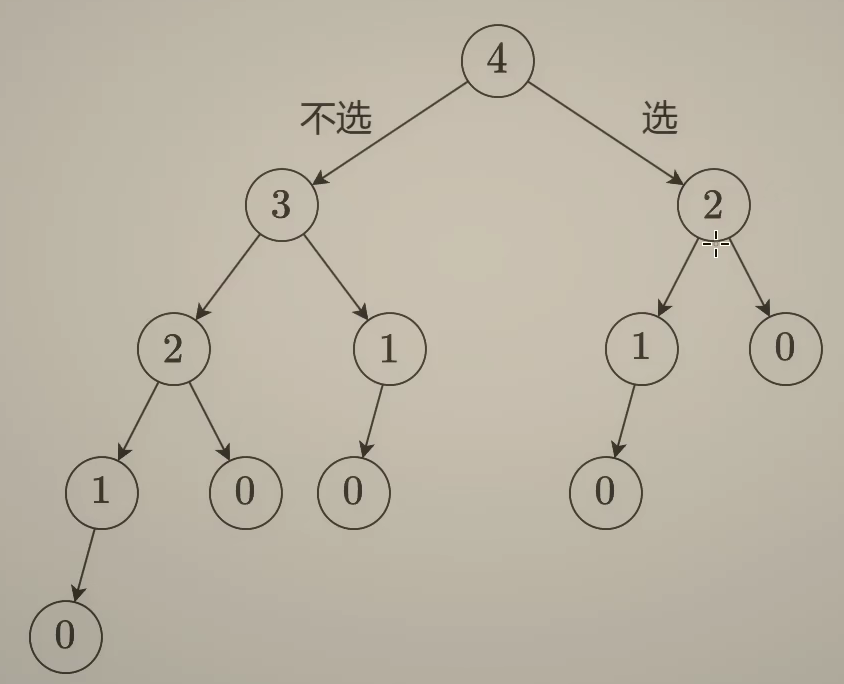
cpp
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
return dfs(n-1,nums);
}
int dfs(int i,vector<int> nums){
if(i<0) return 0;
return max(dfs(i-1,nums),dfs(i-2,nums)+nums[i]);
}
};2.改成记忆化搜索
就例如2已经多次进行了完整的dfs,可以进行了一次的时候就将其记录在缓存数组中,有用则调用
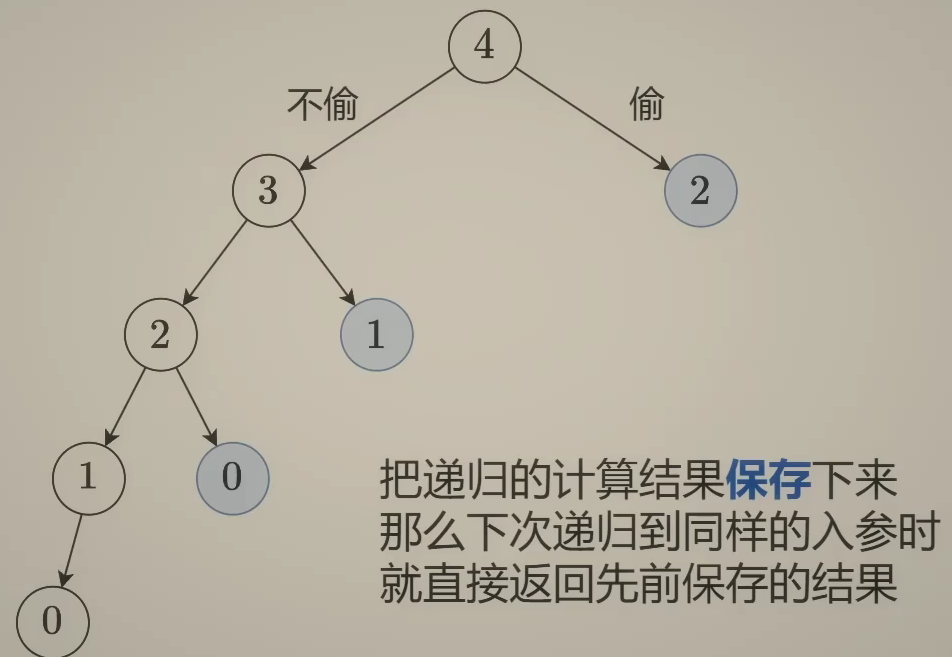
cpp
class Solution {
public:
vector<int> memo;
int rob(vector<int>& nums) {
int n = nums.size();
memo.resize(n,-1);
return dfs(n-1,nums);
}
int dfs(int i,vector<int> nums){
if(i<0) return 0;
if(memo[i]!=-1) return memo[i];
int res = max(dfs(i-1,nums),dfs(i-2,nums)+nums[i]);
memo[i] = res;
return res;
}
};3.1:1翻译成递推
既然我们知道从哪个点可以"归到哪个点",那我们就舍弃"递"的过程,就直接"归",3=2+1,4=3+2,也可以是是自下而上去递,这就叫"递推"
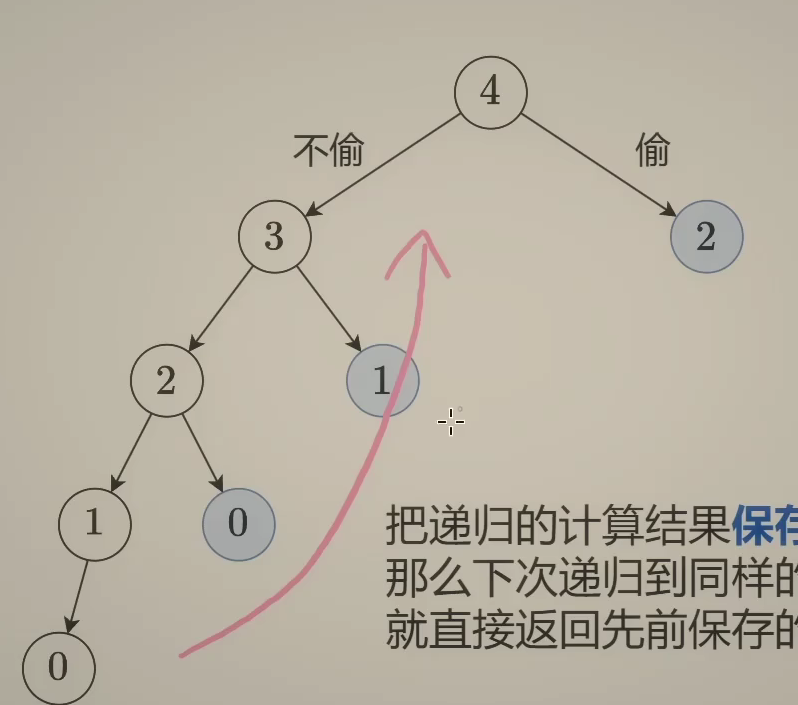

f为dfs的结果数组
自下而上,当前点不选就意味着选下面的点
cpp
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
vector<int> merge(n,-1);
if(n==1) return nums[0];
else if(n==2) return max(nums[0],nums[1]);
merge[0]=nums[0];
merge[1]=max(nums[0],nums[1]);
for(int i=2;i<=n-1;i++)merge[i] = max(merge[i-1],merge[i-2]+nums[i]);
return merge[n-1];
}
};因为只涉及了三个变量可以再进一步优化为空间复杂度为O(1)
cpp
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
int a,b,c;
if(n==1) return nums[0];
else if(n==2) return max(nums[0],nums[1]);
a=nums[0];
b=max(nums[0],nums[1]);
for(int i=2;i<=n-1;i++){
c = max(b,a+nums[i]);
a=b;
b=c;
}
return c;
}
};二.0-1背包
1.每种只能选一个

cpp
int findTargetSumWays(vector<int>& weight, vector<int>& value,int c) {
return dfs(weight,value,c,weight.size()-1);
}
int dfs(vector<int>& weight, vector<int>& value,int c,int i){
if(i<0) return 0;
if(c<weight[i]) return dfs(weight,value,c,i-1);
return max(dfs(weight,value,c,i-1),dfs(weight,value,c-weight[i],i-1)+value[i]);
}2.leetcode 102题
1.分析状态转移方程
2.写出dfs
3.写出递推
1.创建同dfs结果值的f数组,并为其以边界条件附初始值,边界
2.循环(对每个点选或不选)为f数组赋值,循环
3.优化空间复杂度(一般来说,空间都能优化到影响的变量数-1维),优化
java
class Solution {
// 从个体,选or不选,状态转移,转为递推
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i:nums) sum+=i;
sum+=target;
//假设添加正号的数的和是p,添加负号的数就是数组和s-p,所以target = p-(s-p) = 2p-s,则p = (target+s)/2
// 1.target+p一定为偶数,2.且大于等于0
if(sum<0||sum%2==1) return 0;
return dfs(nums,sum/2,nums.length-1);
}
public int dfs(int[] nums,int t,int n){
if(n<0) return t==0?1:0;
if(t<nums[n]) return dfs(nums,t,n-1);
else return dfs(nums,t,n-1)+dfs(nums,t-nums[n],n-1);
}
}1.递推,两行解决
java
class Solution {
// 从个体,选or不选,状态转移,转为递推
public int findTargetSumWays(int[] nums, int target) {
int sum = 0,n = nums.length;
for(int i:nums) sum+=i;
sum+=target;
//假设添加正号的数的和是p,添加负号的数就是数组和s-p,所以target = p-(s-p) = 2p-s,则p = (target+s)/2
// 1.target+p一定为偶数,2.且大于等于0
if(sum<0||sum%2==1) return 0;
sum /= 2;
int[][] f = new int[2][sum+1];
f[0][0] = 1;
// n:i==0时即N<0时
// n\sum 0 1 2 3 4...
// n<0
// 1
for(int i=0;i<n;i++){
// sum
for(int j=0;j<=sum;j++){
if(j<nums[i]) f[(i+1)%2][j] = f[i%2][j];
else f[(i+1)%2][j] = f[i%2][j]+f[i%2][j-nums[i]];
}
}
return f[n%2][sum];
}
}2.递推优化空间为一行
plain
class Solution {
// 从个体,选or不选,状态转移,转为递推
public int findTargetSumWays(int[] nums, int target) {
int sum = 0,n = nums.length;
for(int i:nums) sum+=i;
sum+=target;
//假设添加正号的数的和是p,添加负号的数就是数组和s-p,所以target = p-(s-p) = 2p-s,则p = (target+s)/2
// 1.target+p一定为偶数,2.且大于等于0
if(sum<0||sum%2==1) return 0;
sum /= 2;
int[] f = new int[sum+1];
// 下一层只依赖上层,不依赖本层
f[0] = 1;
for(int i=0;i<n;i++){
// 这里再j<nums[i]停止循环的原因,就是当满足此条件直接等于上层值
for(int j=sum;j>=nums[i];j--){
f[j] = f[j-nums[i]]+f[j];
}
}
return f[sum];
}
}3.leetcode 494题
这里也是选择在哪加正号,是选或不选的问题-》01背包
设选正数的和为p,总和为s,则负数和为s-p,那么t=p-(s-p)=2p-s,则右面为常量式子p=(t+s)/2,那么就转换为,在数组中选出一些正数其和恰好与p即(t+s)/2相等

cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
for(auto i:nums) sum+=i;
sum+=target;
//sum就是t
if(sum<0||sum%2==1) return 0;
return dfs(nums,sum/2,nums.size()-1);
}
int dfs(vector<int>& nums, int target,int i){
if(i<0) return target==0?1:0;
if(target<0) return 0;
return dfs(nums,target,i-1)+dfs(nums,target-nums[i],i-1);
}
};每个结点向下是选或不选,确定下一个结点,再调用dfs返回选或不选的dfs结果之和
转换为递推 1.两个影响dfs结果的变量,target,i 3.初始值是i<0时 c=0时此时加一,因为i<0取不到,所以i再往上扩展一层使其为i=0,其实是i=-1
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size();
int sum=0;
for(auto i:nums) sum+=i;
sum+=target;
//sum就是t
if(sum<0||sum%2==1) return 0;
sum/=2;
vector<vector<int>> ves(n+1, vector<int>(sum+1,0));
ves[0][0] = 1;
for(int i=0;i<n;i++){
for(int j=0;j<=sum;j++){
if(j<nums[i]) ves[i+1][j]=ves[i][j];
else ves[i+1][j] = ves[i][j]+ves[i][j-nums[i]];
}
}
return ves[n][sum];
}
};空间优化,只用两个数组
要计算i+1这个数组的值那么i-1这个数组就用不到了,可以直接将i-1替换为i+1数组

就是对两个数组进行切换%2就可以
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size();
int sum=0;
for(auto i:nums) sum+=i;
sum+=target;
//sum就是t
if(sum<0||sum%2==1) return 0;
sum/=2;
vector<vector<int>> ves(2, vector<int>(sum+1,0));
ves[0][0] = 1;
for(int i=0;i<n;i++){
for(int j=0;j<=sum;j++){
if(j<nums[i]) ves[(i+1)%2][j]=ves[i%2][j];
else ves[(i+1)%2][j] = ves[i%2][j]+ves[i%2][j-nums[i]];
}
}
return ves[n%2][sum];
}
};那能不能只用一个数组呢?
先从左向右算,如下图会把前面的给覆盖掉

那么从右向左算呢?
可以且不会被覆盖
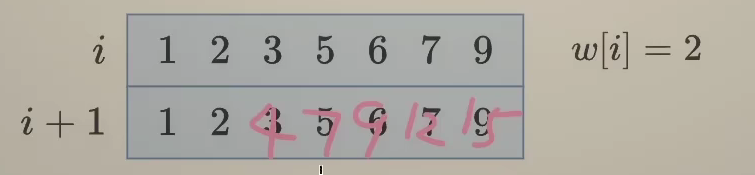
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size();
int sum=0;
for(auto i:nums) sum+=i;
sum+=target;
//sum就是t
if(sum<0||sum%2==1) return 0;
sum/=2;
vector<int> ves(sum+1,0);
ves[0] = 1;
//反过来不越界的技巧
for(int i=0;i<n;i++){
for(int j=sum;j>=nums[i];j--){
ves[j] = ves[j]+ves[j-nums[i]];
}
}
return ves[sum];
}
};三.完全背包
1.LeetCode322题
选n种物品,选了还能选


写出dfs超时
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
int ans = dfs(coins,amount,n-1);
return ans==1000000?-1:ans;
}
int dfs(vector<int>& coins, int amount,int i){
if(i<0){
if(amount==0) return 0;
else return 1000000;
}
if(amount<coins[i]) return dfs(coins,amount,i-1);
return min(dfs(coins,amount,i-1),dfs(coins,amount-coins[i],i)+1);
}
};改成高维数组
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
vector<vector<int>> ves(n+1,vector<int>(amount+1,1000000));
//实际上是i==-1
ves[0][0] = 0;
for(int i=1;i<=n;i++){
for(int j=0;j<=amount;j++){
if(j<coins[i-1]) ves[i][j] = ves[i-1][j];
else ves[i][j] = min(ves[i-1][j],ves[i][j-coins[i-1]]+1);
}
}
return ves[n][amount]==1000000?-1:ves[n][amount];
}
};减少数组空间复杂度
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
vector<vector<int>> ves(2,vector<int>(amount+1,1000000));
//实际上是i==-1
ves[0][0] = 0;
for(int i=1;i<=n;i++){
for(int j=0;j<=amount;j++){
if(j<coins[i-1]) ves[i%2][j] = ves[(i-1)%2][j];
else ves[i%2][j] = min(ves[(i-1)%2][j],ves[i%2][j-coins[i-1]]+1);
}
}
return ves[n%2][amount]==1000000?-1:ves[n%2][amount];
}
};为数组降维
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
vector<int> ves(amount+1,1000000);
//实际上是i==-1
ves[0] = 0;
for(int i=1;i<=n;i++){
for(int j=coins[i-1];j<=amount;j++){
ves[j] = min(ves[j],ves[j-coins[i-1]]+1);
}
}
return ves[amount]==1000000?-1:ves[amount];
}
};最终优化什么是时候向前向后?
状态转移方程依赖,i的前,i的中,倒序:因为这样才能不影响i慢慢向前
状态转移方程依赖,i的前,i+1的前,正序:因为这样才能去依赖i+1慢慢向前
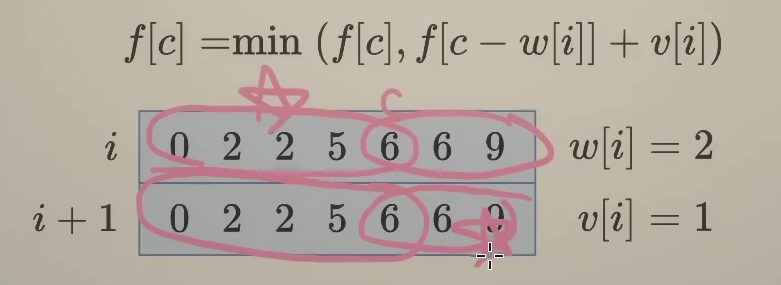
四.线性背包
1.LeetCode1143题:最长公共子串
写出dfs
cpp
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int n = text1.size(),m = text2.size();
return dfs(text1,text2,n-1,m-1);
}
int dfs(string text1, string text2,int i,int j){
if(i<0||j<0) return 0;
if(text1[i]==text2[j]) return dfs(text1,text2,i-1,j-1)+1;
else return max(dfs(text1,text2,i,j-1),dfs(text1,text2,i-1,j));
}
};转为二维递推
cpp
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int n = text1.size(),m = text2.size();
vector<vector<int>> f(n+1,vector<int>(m+1,0));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j] = text1[i-1]==text2[j-1]?f[i-1][j-1]+1:max(f[i][j-1],f[i-1][j]);
}
}
return f[n][m];
}
}转为一维递推(加个临时变量)
plain
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int n = text1.size(),m = text2.size();
vector<int> f(m+1,0);
for(int i=1;i<=n;i++){
int pre = f[0];
for(int j=1;j<=m;j++){
int tmp = f[j];
f[j] = text1[i-1]==text2[j-1]?pre+1:max(f[j-1],f[j]);
pre = tmp;
}
}
return f[m];
}
}2.LeetCode72题:编辑距离
dfs
cpp
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(),m = word2.size();
return dfs(word1,word2,n-1,m-1);
}
int dfs(string word1, string word2,int i,int j){
if(i<0) return j+1;
if(j<0) return i+1;
if(word1[i]==word2[j]) return dfs(word1,word2,i-1,j-1);
else{
int a=dfs(word1,word2,i-1,j),b=dfs(word1,word2,i,j-1),c=dfs(word1,word2,i-1,j-1);
if(a<=b&&a<=c) return a+1;
else if(b<=c) return b+1;
else return c+1;
}
}
};转为递推
cpp
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(),m = word2.size();
vector<vector<int>> f(n+1,vector<int>(m+1,0));
for(int i=0;i<n+1;i++) f[i][0]=i;
for(int j=0;j<m+1;j++) f[0][j]=j;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(word1[i-1]==word2[j-1]) f[i][j] = f[i-1][j-1];
else{
int a=f[i-1][j],b=f[i][j-1],c=f[i-1][j-1];
f[i][j]=min(min(a,b),c)+1;
}
}
}
return f[n][m];
}
}转为一维
cpp
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(),m = word2.size();
vector<int> f(m+1,0);
for(int j=0;j<m+1;j++) f[j]=j;
for(int i=1;i<=n;i++){
int pre = f[0];
f[0]=i;//每一行初始值都为i
for(int j=1;j<=m;j++){
int tmp = f[j];
if(word1[i-1]==word2[j-1]) f[j] = pre;
else{
int a=f[j],b=f[j-1],c=pre;
f[j]=min(min(a,b),c)+1;
}
pre = tmp;
}
}
return f[m];
}
}3.LeetCode300题: 最长递增子序列
dfs实现
cpp
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
int ans = 0;
for(int i=0;i<n;i++) ans = max(ans,dfs(nums,i));
return ans;
}
int dfs(vector<int>& nums,int n){
if(n==0) return 1;
int ans = 0;
for(int i=0;i<n;i++) if(nums[n]>nums[i]) ans = max(ans,dfs(nums,i));
return ans+1;
}
};转为递推
cpp
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
int ans = 0;
vector<int> f(n,0);
f[0]=1;
for(int i=0;i<n;i++){
int res = 0;
for(int j=0;j<i;j++){
if(nums[i]>nums[j]) res = max(res,f[j]);
}
f[i] = res+1;
}
for(int i=0;i<n;i++) ans = max(ans,f[i]);
return ans;
}
}思路三:把数组排序去重后把它与原数组计算一个最长公共子序列得到的就是最长递增子序列,如果最长递增子序列允许重复就不用去重了
Dilworth 定理
把序列分成不递增子序列的最少个数==序列的最长递增子序列长度。
五.树形dp
1.LeetCode543题:二叉树的直径
cpp
class Solution {
public:
int ans = 0;
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
return ans;
}
//计算左右子树的最大深度
int dfs(TreeNode* root){
if(root==nullptr) return -1;
int left = dfs(root->left);
int right = dfs(root->right);
ans = max(ans,left+right+2);
return max(left,right)+1;
}
};2.Leetcode124题:二叉树的最大路径和(直径变题)
cpp
class Solution {
public:
int ans = -9999;
int maxPathSum(TreeNode* root) {
dfs(root);
return ans;
}
int dfs(TreeNode* root){
if(root==nullptr) return 0;
int left_val = dfs(root->left);
int right_val = dfs(root->right);
ans = max(ans,left_val+right_val+root->val);
return max(max(left_val,right_val)+root->val,0);
}
};3.LeetCode2246:相邻字符不同的最长路径(类内函数的使用防止内存溢出)
cpp
class Solution {
public:
int longestPath(vector<int> &parent, string &s) {
int n = parent.size();
vector<vector<int>> g(n);
for (int i = 1; i < n; ++i)
g[parent[i]].push_back(i);
int ans = 0;
//function<int(int)> 是 C++ 中的一个函数类型,表示一个以 int 为参数类型,返回值为 int 类型的函数。后面加[capture clause] (parameters) -> return_type {函数体}
//类内函数
function<int(int)> dfs = [&](int x) -> int {
int maxLen = 0;
for (int y : g[x]) {
int len = dfs(y) + 1;
if (s[y] != s[x]) {
ans = max(ans, maxLen + len);
maxLen = max(maxLen, len);
}
}
return maxLen;
};
dfs(0);
return ans + 1;
}
};4.Leetcode337题:打家劫舍三(对树的选或不选)
java
class Solution {
public:
unordered_map <TreeNode*, int> f, g;
void dfs(TreeNode* node) {
if (!node) {
return;
}
dfs(node->left);
dfs(node->right);
f[node] = node->val + g[node->left] + g[node->right];
g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
}
int rob(TreeNode* root) {
dfs(root);
return max(f[root], g[root]);
}
};六.状态机dp
其他
1.LeetCode5题最长回文子串
java
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
int length = 1; // 最长回文子串的长度
int start = 0; // 最长回文子串的起始位置
boolean[][] dp = new boolean[n][n]; // dp[j][i]表示子串s[j:i]是否为回文串
for(int i = 0; i < n; i++){
// 以i为终点,往回枚举起到j
for(int j=i;j>=0;j--){
if(i==j) dp[j][i] = true;
else if(i==j+1) dp[j][i] = (s.charAt(i)==s.charAt(j));
else dp[j][i] = (s.charAt(i)==s.charAt(j))&& dp[j+1][i-1];
if(dp[j][i] && (i-j+1)>length){
length = i-j+1;
start = j;
}
}
}
return s.substring(start,start+length);
}
}二分查找
在g找x的左边界(返回迭代器)查找大于或等于指定值的第一个元素的位置
cpp
auto it = lower_bound(g.begin(), g.end(), x);在g找x的右边界(返回迭代器)查找大于指定值的第一个元素
cpp
auto it = upper_bound(g.begin(), g.end(), x);注意:上述两个方法只有在一定能找到该值才会有效果
取下标
cpp
int m=distance(nums.begin(), sr)*it取值
也可取值并赋值到原数组中
cpp
*it = x;
cpp
class Solution {
public:
int shipWithinDays(vector<int>& weights, int days) {
//获取货物的最大值
int ma = *max_element(weights.begin(),weights.end());
int left = ma;
int right = 1e9;
while(left<right){
int mid = left + (right-left)/2;
if(gerDay(mid,weights)>days) left = mid+1;
else right = mid;
}
return right;
}
//返回该运载量所需要的天数;
int gerDay(int m,vector<int>& weights){
int sumday = 0;
for(int i=0;i< weights.size();){
int weight = m;
while(i<weights.size()&&weight>=weights[i]){
weight-=weights[i];
i++;
}
sumday+=1;
}
return sumday;
}
};
cpp
class Solution {
public:
int hour;
int f(vector<int>& piles,int x){
long hours = 0;
for (int i = 0; i < piles.size(); i++) {
hours += piles[i] / x;
if (piles[i] % x > 0) {
hours++;
}
}
return hours;
}
int minEatingSpeed(vector<int>& piles, int h) {
hour = h;
long long l=1,r = 1000000000 + 1;
while(l<r){
long long mid = l+(r-l)/2;
if(f(piles,mid)>hour) l = mid+1;
else r = mid;
}
return l;
}
};图论

1.prim
cpp
#include <bits/stdc++.h>
using namespace std;
int n,m,ans = 0;
//一.定义
//1.1
int mapdist[1000][1000];
//1.2
vector<int> v[1000];
//1.3
int mindist[1000];//此时每个点到最短路的长度
//二.prim过程
void prim(){
//2.1定义防回代码
vector<bool> visted(1000,false);
int last = 1;
mindist[last] = 0;
for(int i=1;i<=n;i++){
visted[last] = true;
//2.2.1核心代码 扩散该节点
for(int j=1;j<=n;j++) mindist[j] = min(mindist[j],mapdist[last][j]);
int k=-1;
//2.2.2找到下一个最短举例节点
for(int j=1;j<=n;j++) if(!visted[j]&&(k<0||mindist[j]<mindist[k])) k=j;
last = k;
//不同代码,最短路的最终路径
ans+=mindist[k];
}
}
int main()
{
cin>>n>>m;
//1.4 初始化举例
memset(mapdist,0x3f,sizeof(mapdist));
memset(mindist,0x3f,sizeof(mindist));
for(int i=0;i<m;i++){
int v1,v2,d;
cin>>v1>>v2>>d;
v[v1].push_back(v2);
v[v2].push_back(v1);
mapdist[v1][v2] = mapdist[v2][v1] = d;
}
prim();
cout<<ans;
return 0;
}2.dijisktra

java
#include<bits/stdc++.h>
using namespace std;
int n,m,c1,c2;
int zyrenshu=0;
int pathsize=0;
int renshu[500];
//1.定义
//1.1距离
int mapdist[500][500];
//1.2结点
vector<int> v[500];
//1.3最短路
int mindist[500];
//2.构造
void dijikstra(){
//2.1检验防回数组
vector<int> visited(n,false);
int last = c1;
mindist[last] = 0;
for(int i=0;i<n;i++){
visited[last] = true;
//2.2.1扩散
for(int j=0;j<n;j++) mindist[j] = min(mindist[j],mindist[last]+mapdist[j][last]);
//2.2.2寻找
int k=-1;
for(int j=0;j<n;j++) if(!visited[j]&&(k<0||mindist[j]<mindist[k])) k=j;
last = k;
}
}
//3.dfs
void dfs(int cur,int changdu,int curzyrenshu){
if(mindist[cur]<changdu) return;
if(cur==c2){
pathsize++;
zyrenshu = max(zyrenshu,curzyrenshu);
}else for(auto m:v[cur]) dfs(m,changdu+mapdist[m][cur],renshu[m]+curzyrenshu);
}
int main(){
cin>>n>>m>>c1>>c2;
//1.4
memset(mapdist,0x3f,sizeof(mapdist));
memset(mindist,0x3f,sizeof(mindist));
for(int i=0;i<n;i++) cin>>renshu[i];
for(int i=0;i<m;i++){
int v1,v2,d;
cin>>v1>>v2>>d;
v[v1].push_back(v2);
v[v2].push_back(v1);
mapdist[v1][v2] = mapdist[v2][v1] = d;
}
dijikstra();
dfs(c1,0,renshu[c1]);
cout<<pathsize<<" "<<zyrenshu;
}3.并查集
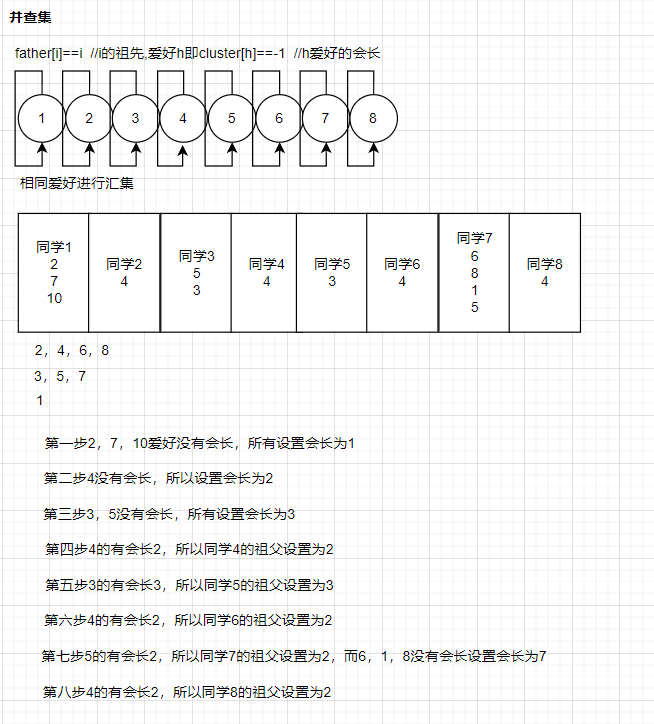
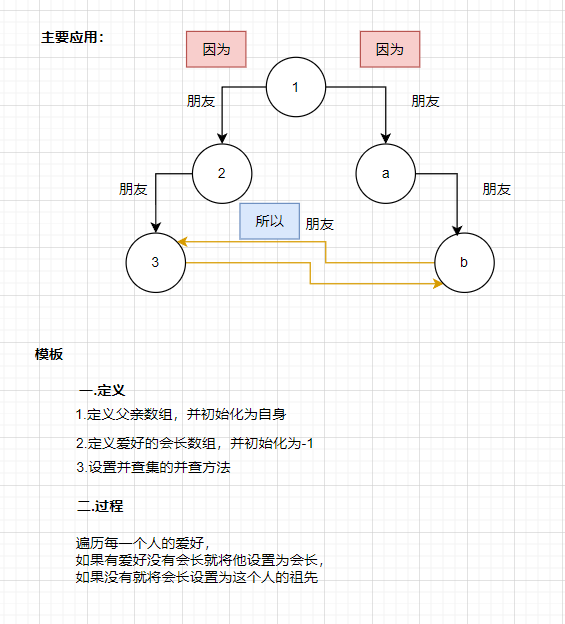
cpp
//将开启爱好圈子的第一个人作为标杆,相同爱好的人有相同的标杆,相同人的不同爱好有相同的标杆
#include<bits/stdc++.h>
using namespace std;
int father[1001]={0},cluster[1001]={0};
vector<int> isroot(1001,0);
int n;
int findfather(int x){
if(x!=father[x]) father[x] = findfather(father[x]);
return father[x];
}
void _union(int x,int y){
if(findfather(x)!=findfather(y)) father[findfather(x)] = findfather(y);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) father[i] = i;
for(int i=1;i<=n;i++){
int k;
cin>>k;
getchar();
for(int j=0;j<k;j++){
int h;
cin>>h;
if(cluster[h]==0) cluster[h] = i;
_union(i,findfather(cluster[h]));
}
}
for(int i=1;i<=n;i++) isroot[findfather(i)]++;
sort(isroot.begin(),isroot.end(),greater<int>());
int sum=0;
for(int i=0;i<n;i++){
if(isroot[i]!=0) sum++;
else break;
}
cout<<sum<<endl;
for(int i=0;i<sum;i++){
if(!i) cout<<isroot[i];
else cout<<" "<<isroot[i];
}
}树
完全二叉树
判断用bfs
plain
bool t = true;
void level(TreeNode* root){
if(root==nullptr) return;
queue<TreeNode*> q;
q.push(root);
bool t1=true;
while(!q.empty()){
TreeNode* cur = q.front();
q.pop();
le.push_back(cur->data);
if(cur->left==nullptr){
if(t1) t1 = false;
}else{
if(!t1) t = false;
q.push(cur->left);
}
if(cur->right==nullptr){
if(t1) t1 = false;
}else{
if(!t1) t = false;
q.push(cur->right);
}
}
}
if(!t) "那么就不是完全二叉树" else "就是完全二叉树"二叉搜索树
左小右大
遍历:BST 的中序遍历其实就是升序排序的结果
cpp
void BST(TreeNode* root, int target) {
if(root==nullptr) return;
if (root->val == target)
// 找到目标,做点什么
if (root->val < target)
BST(root->right, target);
if (root->val > target)
BST(root->left, target);
}构造:
cpp
TreeNode* BSTbuild(int start,int end){
if(start>end) return nullptr;
TreeNode* root = new TreeNode(treenums[start]);
int mid=-1;
for(int i=start+1;i<=end;i++){
if(treenums[start]<=treenums[i]){
mid = i;
break;
}
}
if(mid==-1) root->left = BSTbuild(start+1,end);
else{
root->left = BSTbuild(start+1,mid-1);
root->right = BSTbuild(mid,end);
}
return root;
}树的遍历
层序
cpp
void levelTravese(){
queue<int> q;
q.push(root);
int num = 0;
while (!q.empty()){
int top = q.front();
q.pop();
printf("%d",top);
if(num<N-1) printf(" ");
++num;
if(tree[top].right!=-1){
q.push(tree[top].right);
}
if(tree[top].left!=-1){
q.push(tree[top].left);
}
}
}树的构造
前中-》
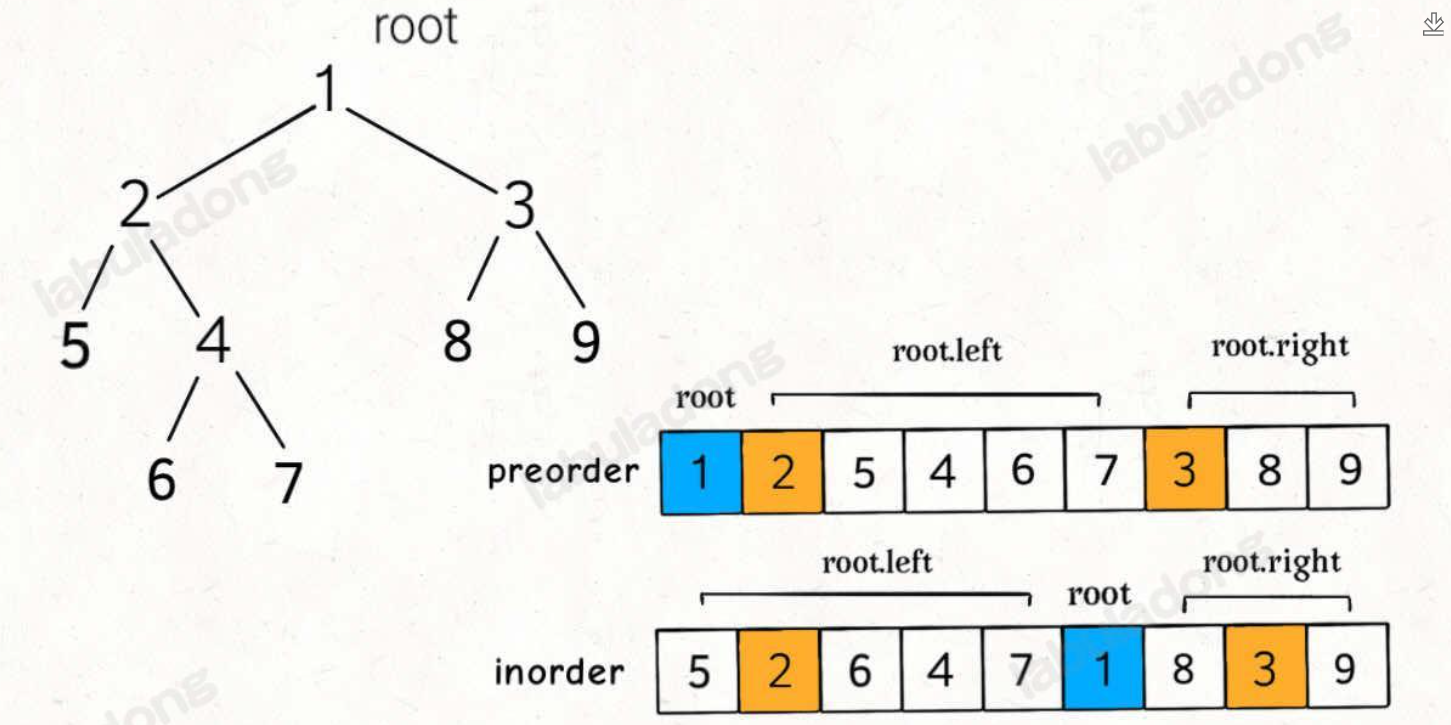
cpp
TreeNode* gouzao(vector<int> &preorder,int prestart,int preend,vector<int> &inorder,int instart,int inend){
if(prestart>preend) return nullptr;
TreeNode* root= new TreeNode(preorder[prestart]);
int index = -1;
for(int i=instart;i<=inend;i++){
if(inorder[i]==preorder[prestart]){
index = i;
break;
}
}
int cha = index-instart;
//注意去开头之后的长度为插值
root->left = gouzao(preorder,prestart+1,prestart+cha,inorder,instart,index-1);
root->right = gouzao(preorder,prestart+cha+1,preend,inorder,index+1,inend);
return root;
}
cpp
#include<bits/stdc++.h>
using namespace std;
struct TreeNode{
int val;
TreeNode *left=nullptr,*right=nullptr;
TreeNode(int val){
this->val = val;
}
};
int n;
vector<int> preorder,inorder,postorder;
stack<int> st;
TreeNode* build(vector<int> &preorder,int prestart,int preend,vector<int> &inorder,int instart,int inend){
if(prestart>preend) return nullptr;
TreeNode* root= new TreeNode(preorder[prestart]);
int index = -1;
for(int i=instart;i<=inend;i++){
if(inorder[i]==preorder[prestart]){
index = i;
break;
}
}
int cha = index-instart;
root->left = gouzao(preorder,prestart+1,prestart+cha,inorder,instart,index-1);
root->right = gouzao(preorder,prestart+cha+1,preend,inorder,index+1,inend);
return root;
}
void posttraverse(TreeNode* root){
if(root==nullptr) return;
posttraverse(root->left);
posttraverse(root->right);
postorder.push_back(root->val);
}
int main(){
//由前序中序构造二叉树-》后序遍历
cin>>n;
string m1;
int m2;
for(int i=1;i<=2*n;i++){
cin>>m1;
if(m1=="Push"){
cin>>m2;
preorder.push_back(m2);
st.push(m2);
}else{
inorder.push_back(st.top());
st.pop();
}
}
TreeNode* root = build(preorder,0,n-1,inorder,0,n-1);
posttraverse(root);
for(int i=0;i<n;i++){
if(!i) cout<<postorder[i];
else cout<<" "<<postorder[i];
}
}中后 如果参数是数组int (&post)[40]
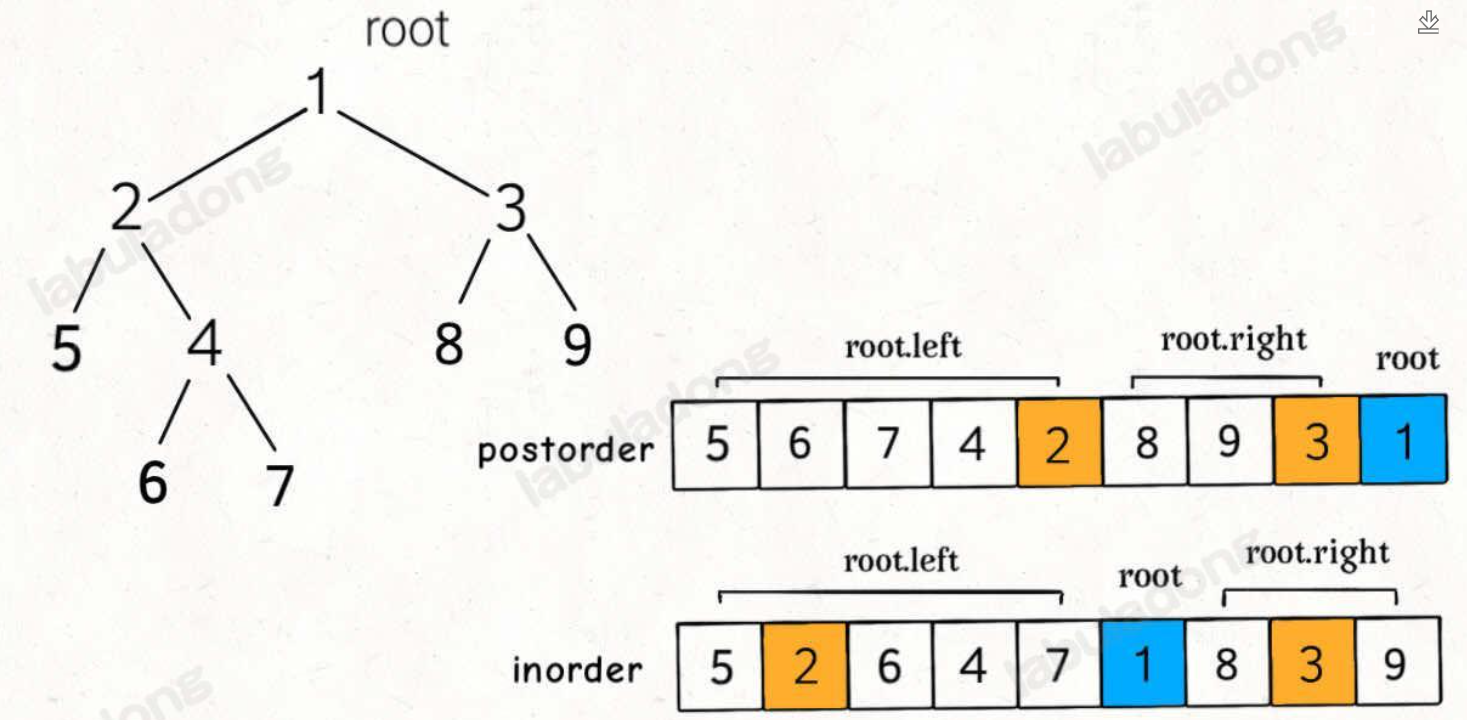
cpp
TreeNode* build(vector<int> &in,int instart,int inend,vector<int>post,int poststart,int postend){
if(poststart>postend) return nullptr;
TreeNode *root = new TreeNode(post[postend]);
int index;
for(int i=instart;i<=inend;i++){
if(in[i]==post[postend]){
index = i;
break;
}
}
int charzhil = index - instart;
//注意去结尾之后的长度为插值
root->l = gouzao(in,instart,index-1,post,poststart,poststart+charzhil-1);
root->r = gouzao(in,index+1,inend,post,poststart+charzhil,postend-1);
return root;
}LCA
cpp
TreeNode* zhao_zi(TreeNode* root,int val1,int val2){
if(root==nullptr) return nullptr;
if(root->val==val1||root->val==val2) return root;
TreeNode* left=lca(root->left,val1,val2);
TreeNode* right=lca(root->right,val1,val2);
if(left!=nullptr&&right!=nullptr) return root;
return left==nullptr?right:left;
}
cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
int s[10001];
unordered_set<int> se;
struct TreeNode{
int val;
TreeNode* left = nullptr,*right = nullptr;
TreeNode(int val){
this->val = val;
}
};
TreeNode* build(int start,int end){
if(start>end) return nullptr;
TreeNode* root = new TreeNode(s[start]);
int index=-1;
for(int i=start+1;i<=end;i++){
if(root->val<=s[i]){
index = i;
break;
}
}
if(index!=-1){
root->left = build(start+1,index-1);
root->right = build(index,end);
}else{
root->left = build(start+1,end);
}
return root;
}
TreeNode* lca(TreeNode* root,int val1,int val2){
if(root==nullptr) return nullptr;
if(root->val==val1||root->val==val2) return root;
TreeNode* left=lca(root->left,val1,val2);
TreeNode* right=lca(root->right,val1,val2);
if(left!=nullptr&&right!=nullptr) return root;
return left==nullptr?right:left;
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++){
cin>>s[i];
se.insert(s[i]);
}
TreeNode* root = build(0,m-1);;
int a1,a2;
for(int i=0;i<n;i++){
cin>>a1>>a2;
if(se.find(a1)==se.end()&&se.find(a2)==se.end()) {
cout<<"ERROR: "<<a1<<" and "<<a2<<" are not found."<<endl;
continue;
}
if(se.find(a1)==se.end()){
cout<<"ERROR: "<<a1<<" is not found."<<endl;
continue;
}
if(se.find(a2)==se.end()){
cout<<"ERROR: "<<a2<<" is not found."<<endl;
continue;
}
TreeNode* root1 = lca(root,a1,a2);
if(root1->val==a1){
cout<<a1<<" is an ancestor of "<<a2<<"."<<endl;
}else if(root1->val==a2){
cout<<a2<<" is an ancestor of "<<a1<<"."<<endl;
}else{
cout<<"LCA of "<<a1<<" and "<<a2<<" is "<<root1->val<<"."<<endl;
}
}
}排序
快排
1.quickSort:
排左排右dfs
2.partition:
(1)随机选取建立一个标签srand(time(0));int m = rand()%(R-L+1) + L;
(2)初始化p1=l,p2=r,i=l流程:与随机数哨兵相等i++,小于哨兵p1++,i++,大于哨兵 p2++;
(3)返回vector { p1-1, p2+1 };
cpp
#include<bits/stdc++.h>
using namespace std;
void swap(int &a,int&b){
if(a==b) return;
a = a^b;
b = a^b;
a = a^b;
}
vector<int> partition(vector<int>& nums, int L, int R){
srand(time(0));
int m = rand()%(R-L+1) + L;
m = nums[m];
int p1 = L, p2 = R, i = L;
while (i <= p2) {
if (nums[i] < m) {
swap(nums[i], nums[p1]);
p1++;
i++;
} else if (nums[i] > m) {
swap(nums[i], nums[p2]);
p2--;
} else {
i++;
}
}
return vector<int> { p1-1, p2+1 };
}
//前序遍历
void quickSort(vector<int>& nums, int L, int R) {
if(L>=R) return;
vector<int> m = partition(nums,L,R);
quickSort(nums,L,m[0]);
quickSort(nums,m[1],R);
}
int main(){
vector<int>nums = {9,9,1,8,2,3,1};
quickSort(nums,0,nums.size()-1);
for(auto i:nums) cout<<" "<<i;
} 归并
1.sort找中间,排左排右,后序位置进行merge
2.merge:(1)定义一个临时数组为临时数组赋初值(原数组)
(2)左,中放个指针,p临时数组指针,num随推进修改
cpp
#include <bits/stdc++.h>
using namespace std;
vector<int> temp;
void merge(vector<int>& nums,int left,int mid,int right){
for(int i=left;i<=right;i++) temp[i] = nums[i];
int i = left,j = mid+1,p=left;
while(p<=right){
if(i==mid+1) nums[p++] = temp[j++];
else if(j==right+1) nums[p++] = temp[i++];
else if(temp[i]<=temp[j]) nums[p++] = temp[i++];
else if(temp[i]>temp[j]) nums[p++] = temp[j++];
}
}
//后续遍历
void sort(vector<int>& nums,int left,int right){
if(right<=left) return;
int mid = left+(right-left)/2;
sort(nums,left,mid);
sort(nums,mid+1,right);
merge(nums,left,mid,right);
}
int main(){
vector<int>nums = {0,9,1,3,9,6,8,6,1};
int n = nums.size();
temp.resize(n);
sort(nums,0,n-1);
for(auto i:nums) cout<<" "<<i;
}逆序对

cpp
#include <iostream>
#include <vector>
using namespace std;
vector<int> temp;
int reversePairs = 0;
void merge(vector<int>& nums, int left, int mid, int right) {
for (int i = left; i <= right; i++) temp[i] = nums[i];
int i = left, j = mid + 1, p = left;
while (p <= right) {
if (i == mid + 1) nums[p++] = temp[j++];
else if (j == right + 1) nums[p++] = temp[i++];
else if (temp[i] <= temp[j]) nums[p++] = temp[i++];
else {
nums[p++] = temp[j++];
reversePairs += mid - i + 1; // 统计逆序对数量
}
}
}
void sort(vector<int>& nums, int left, int right) {
if (right <= left) return;
int mid = left + (right - left) / 2;
sort(nums, left, mid);
sort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
int main() {
vector<int> nums = {9, 7, 5, 4, 6};
int n = nums.size();
temp.resize(n);
sort(nums, 0, n - 1);
cout << "逆序对总数:" << reversePairs << endl;
return 0;
}堆排序
cpp
#include <bits/stdc++.h>
using namespace std;
void buildMaxHeap(vector<int>& nums) {
int n = nums.size();
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
//从n-1的父亲节点开始遍历,然后依次自右向左再向上heapfiy 其中n-1为第n个元素的下标为n-1
maxHeapify(nums, i, n);
}
}
void maxHeapify(vector<int>& nums, int i, int n) {
while (i * 2 + 1 < n) {//当至少有一个孩子
// 代表当前 i 节点的左右儿子;
// 超出数组大小则代表当前 i 节点为叶子节点,不需要移位
int lSon = 2 * i + 1;
int rSon = 2 * i + 2;
int large = i;
if (lSon < n && nums[lSon] > nums[large]) large = lSon;
if (rSon < n && nums[rSon] > nums[large]) large = rSon;
if (large != i) {
swap(nums[i], nums[large]);
// 迭代判断对应子节点及其儿子节点的大小关系
i = large;
} else {
break;
}
}
}
vector<int> sortArray(vector<int>& nums) {
// heapSort 堆排序
int n = nums.size();
// 将数组整理成大根堆
buildMaxHeap(nums);
for (int i = n - 1; i >= 1; --i) {
// 依次弹出最大元素,放到数组最后,当前排序对应数组大小 - 1
swap(nums[0], nums[i]);
--n;
maxHeapify(nums, 0, n);
}
return nums;
}
int main(){
sortArray(num);
}数字运算技巧
1.最大公约数与最小公倍数
cpp
/*
求两个正整数 a 和 b 的 最大公约数 d
则有 gcd(a,b) = gcd(b,a%b)
证明:
设a%b = a - k*b 其中k = a/b(向下取整)
若d是(a,b)的公约数 则知 d|a 且 d|b 则易知 d|a-k*b 故d也是(b,a%b) 的公约数
若d是(b,a%b)的公约数 则知 d|b 且 d|a-k*b 则 d|a-k*b+k*b = d|a 故而d|b 故而 d也是(a,b)的公约数
因此(a,b)的公约数集合和(b,a%b)的公约数集合相同 所以他们的最大公约数也相同 证毕#
*/
int gcd(int a, int b) return b ? gcd(b,a%b):a; 最大公约数:gcb(a,b)
由欧几里得辗转相除法:最小公倍数= a*b/gcb(a,b);
b:gcb(b,a%b):a;
2.素数(质数)判断
除1和本身没有其他除数
cpp
bool isPrime(int r) {
if (r <= 1) return false;
for (int i = 2; i <= sqrt(r); i++) if (r % i == 0) return false;
return true;
}由数的对称性(3×2=2×3)得知如果r在【2,r的平方根】之间没有倍数关系那么就为素数
3.进制转换
(1)10进制转r进制
cpp
vector<int> nums;
while (n) {
nums.push_back(n % r);
n /= r;
}
reverse(nums.begin(),nums.end());以10进制转二进制举例:
每余2得到该数在二进制中的最后小位数
每除二相当于在二进制中右一一下
所以循环过后的位数是上升的所以反转
(2)r进制转10进制
cpp
int res = 0;
for (int i = 0; i < nums.size(); i++)
res = res* r + nums[i];相当于先左移再相加最低位
4.Ascll码表
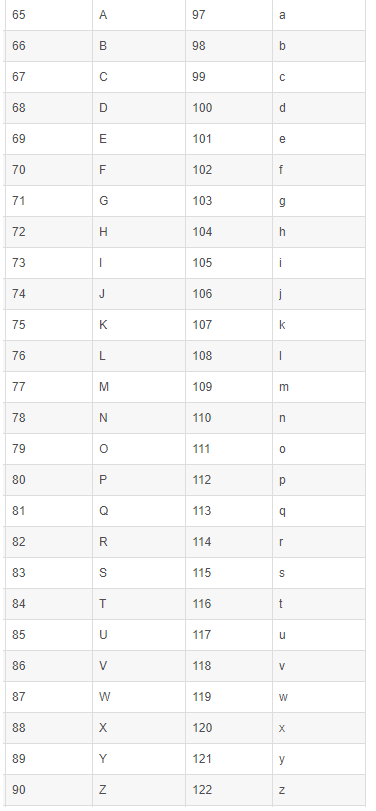
5.高精度数字计算
(1)高精度加法
1.将字符串a,b反向导入到新建A,B数组
2.创建临时变量,并使用t对两个加法操作,对10取余放到C数组,除等
3.将C数组反向导出到c中
cpp
#include<bits/stdc++.h>
using namespace std;
string add(string a,string b){
vector<int>A,B;
for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--)B.push_back(b[i]-'0');
vector<int> C;
int t=0;
for(int i=0;i<A.size()||i<B.size();i++){
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if(t!=0) C.push_back(t);
string c = "";
for (int i = C.size() - 1; i >= 0; i--) {
c+=to_string(C[i]);
}
return c;
}
int main(){
string a= "9999999999999999999999999";
string b = "4324324299999999999999999999999";
cout<<add(a,b);
} (2)高精度减法
条件:a>b
1.将字符串a,b反向导入到新建A,B数组
2.创建临时变量,遍历A数组并使用t对A加法操作,对t+10取10余放到C数组,若t《0 t=-1,则t=0;
3.将C数组反向导出到c中
cpp
#include<bits/stdc++.h>
using namespace std;
string diff(string a, string b) {
vector<int> A, B, C;
for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
int t = 0;
for (int i = 0; i < A.size(); i++) {
t += A[i];
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = -1;
else t = 0;
}
string c;
//if(C.size()>1&&C.back()==0) C.pop_back();
for (int i = C.size() - 1; i >= 0; i--) c += to_string(C[i]);
return c;
}
int main(){
string a= "9990";
string b = "1000";
cout<<diff(a,b);
} (3)高精度乘法
cpp
vector<int> mul(vector<int>& A, int b) {
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i++) {
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}(4)高精度除法
cpp
vector<int> div(vector<int>& A, int b, int& r) {
vector<int> C(A.size());
for (int i = 0; i < A.size(); i++) {
r = r * 10 + A[i];
C[i] = r / b;
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}6.比较器的应用过程
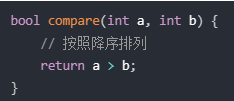
- 返回true不交换
- 返回false交换
7.时间相关
时间安排,都安排成秒,再进行排序,从时间按转化为h:m:s就是
8.字母数字判断以及大小写转化
Isdigit()判断字符是否为数字
isalpha()判断此字符是否为字母
islower()判断此字符是否为小写字母
isupper()判断此字符是否为大写字母
isalnum()判断此字符是否为字母或数字
isspace()判断此字符是否为空格或转换符
如果是则输出1,不是就输出0
tolower()将此字符转为小写字母
toupper()将此字符转为大写字母
9.数字字母转化
字符串转数字
stoi():意思是把字符串转化为int型变量
stod():意思是把字符串转化为double型变量
字符转数字
i=j-'0';
数字转字符串
to_string():这个很简单,也很实用,功能就是把一个数字,只能将数字转化为字符串
字符转字符串
String(1,c):将字符型变成string类型返回字符串类型
10.其他
(1)数组初始化
memset(color,0,sizeof(color)):
第一个参数是开头指针,第二个是赋的值,第三个是所占内存大小
(2)int自动去除前面0
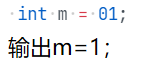
(3)排名重叠问题
如果是排名类的题目呢,有两个第一名就不要出现第二名了

(4)map降序
map容器默认按键大小升序排列,那怎么降序排列呢

(5)两个不等长的字符串比较

(6)四舍五入输出
先×n个10
再round(num);
另外
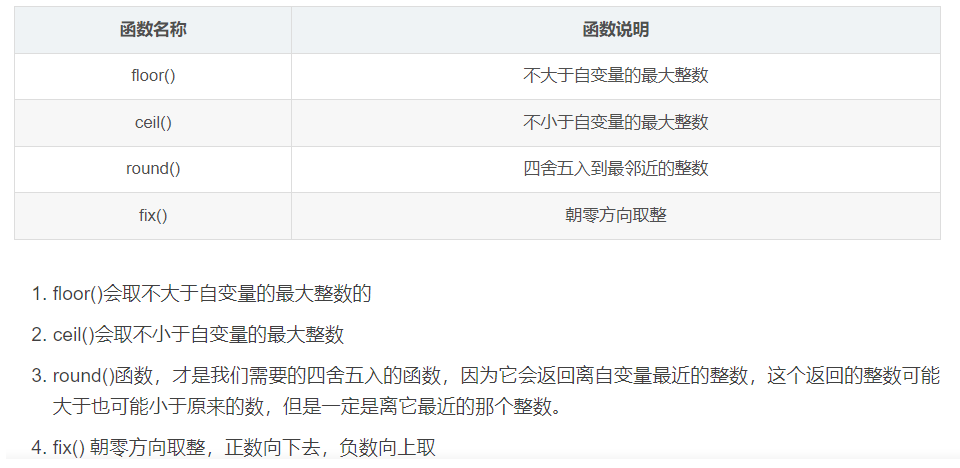
(7)sort取前不取后
Sort(work,work+3);前取后不取[0,3)->[0,2]
(8)输出格式
链接csdn
(9)获取输入
获取输入的一行
cpp
int main(){
string input;
getline(cin,input);
vector<int> numbers;
istringstream iss(input);
int number;
while (iss >> number) {
numbers.push_back(number);
}
}(10)闰年是指
闰年和平年的主要区别在于闰年比平年多一天。具体来说,闰年是指每四年中有一个多出的日子,即2月份有29天而不是28天。
①非世纪年能被4整除,且不能被100整除的是闰年。(如2024年是闰年,1901年不是闰年)
②世纪年能被400整除的是闰年。(如2000年是闰年,1900年不是闰年)
11.优先队列
priority_queue 类模板的三个参数:输入类型为 ListNode*,堆容器类型为 vector<ListNode*>,比较函数类型声明为function<bool(ListNode*, ListNode*)>
方法:
是否为空:Pq.empty()
放入元素:Pq.push()
取堆顶元素:Pq.top()
删掉堆顶元素:Pq.pop()
cpp
priority_queue<ListNode*,vector<ListNode*>,function<bool(ListNode*,ListNode*)>> pq(
[](LustNode* a,ListNode* b){
return a->val > b->val;
});
cpp
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int,vector<int>,function<bool(int,int)>> pq(
[](int a,int b){
return a>b;//每一次比较都是一次向下调整所以是小顶堆
}
);
for (int e : nums) {
pq.push(e);
if (pq.size() > k) pq.pop();//如果大小超过了k就删掉堆顶
}
return pq.top();
}
};