数据结构与算法-前缀和数组

前缀和问题

什么是前缀和?

对于一个一般数组 nums,如果我们需要知道 S1 = nums[0] + nums[1]的结果， S2= nums[0] + nums[1] + nums[2] ...

计算公式相当于: S2 = S1 + nums[2] ... Sn = Sn-1 + nums[n];

所谓前缀和：用来记录数组前项和的一个新数组，提高计算求和的效率。

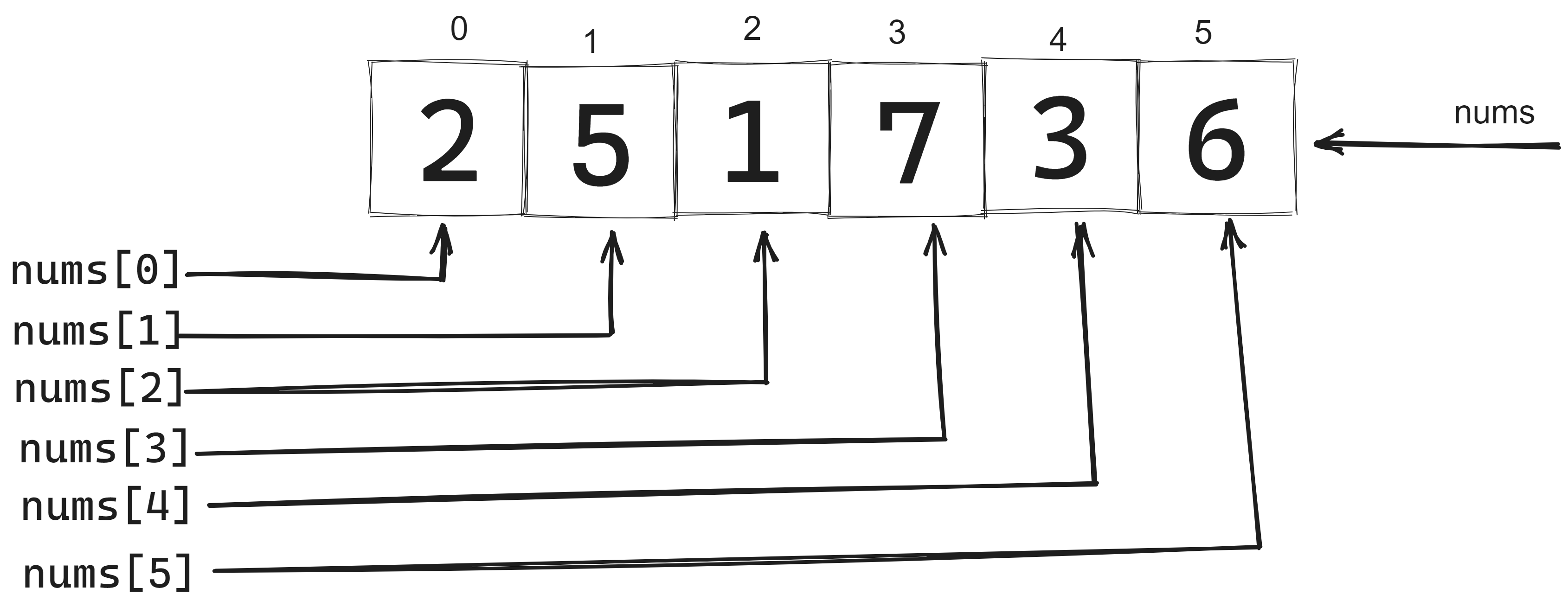
从普通数组转向前缀和数组

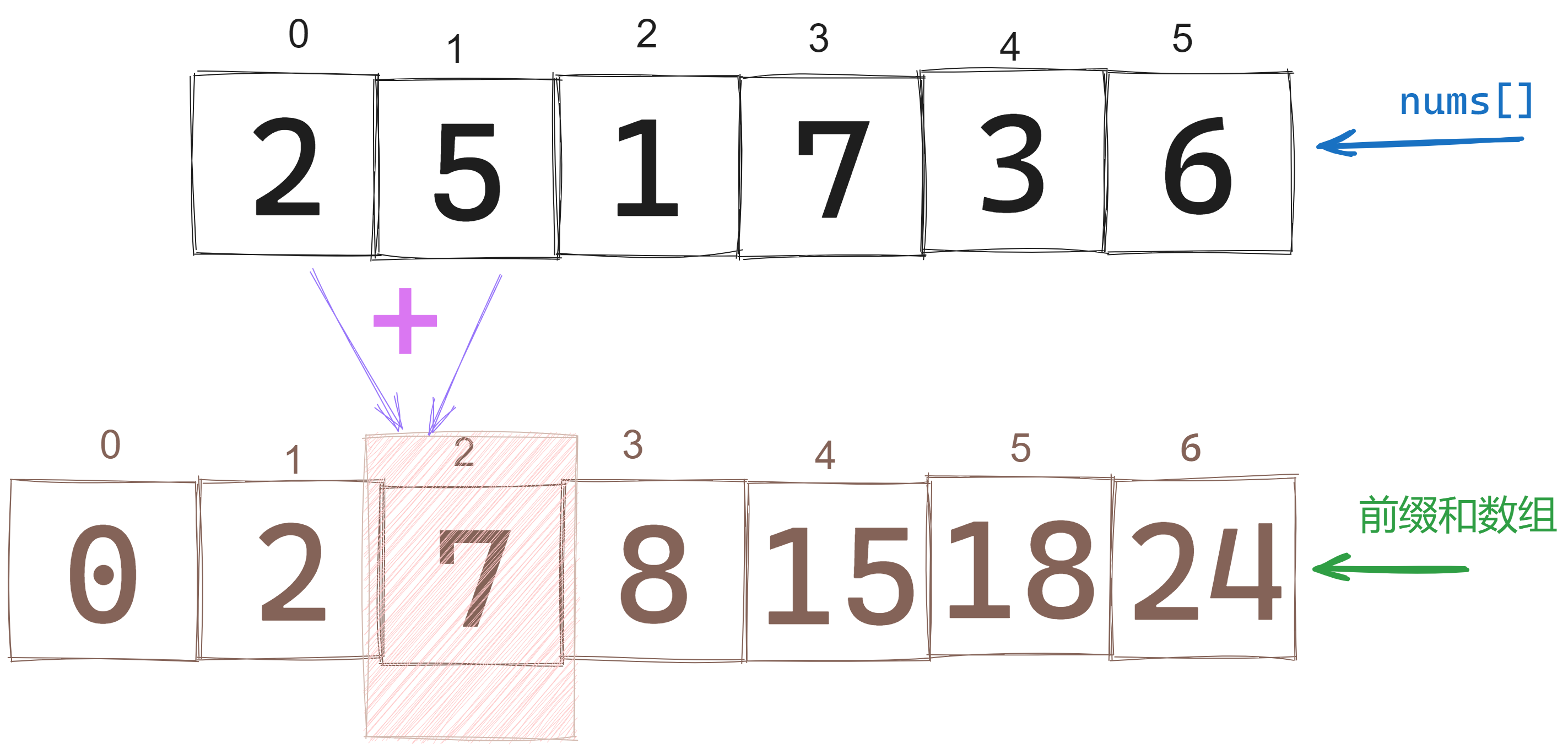
一般递推公式

由前缀和的定义我们可以得出以下前缀和公式：

当前项i的前缀和S[i]

java 复制代码

S[i] = S[i-1] + nums[i-1];

当前项i的数据由前缀和推出

java 复制代码

nums[i-1] = S[i] - S[i-1]

代码实现

java 复制代码

int[] nums = {2,5,1,7,3,6};
int[] s = new int[nums.length+1];

for(int i= 1;i<s.length;i++){
    s[i] = s[i-1]+ nums[i-1];
}

System.out.println(Arrays.toString(nums));
System.out.println(Arrays.toString(s));

输出结果

java 复制代码

[2, 5, 1, 7, 3, 6]
[0, 2, 7, 8, 15, 18, 24]

扩展运用

计算指定位置之间的数据和。

假设数组为 {1，2， 3， 4}，位置1,3之间的和为： 2+3+4 = 9

使用前缀和

列出前缀和数组: {0，1, 3, 6, 10} , 位,1到3之间的和 S[4]- S[1] = 10 -1 = 9

计算任意位置之间的和: S[i+1] - S[j] , tips: 前缀和数组的S[0] =0;

力扣问题

1480. 一维数组的动态和 - 力扣（LeetCode）

java 复制代码

class Solution {
    public int[] runningSum(int[] nums) {
        int[] s = new int[nums.length];
        s[0] = nums[0];
        for (int i = 1; i < s.length; i++) {
            s[i] = s[i - 1] + nums[i];
        }

        return s;
    }
}

303. 区域和检索 - 数组不可变 - 力扣（LeetCode）

java 复制代码

class NumArray {

    private int[] nums;
    private int[] s;

    public NumArray(int[] nums) {
        this.nums = nums;
        this.s = new int[nums.length + 1];
        for (int i = 1; i < s.length; i++) {
            s[i] = s[i - 1] + nums[i - 1];
        }
    }
    
    public int sumRange(int left, int right) {
        return s[right+1] - s[left];
    }
}

560. 和为 K 的子数组 - 力扣（LeetCode）

二维数组前缀和

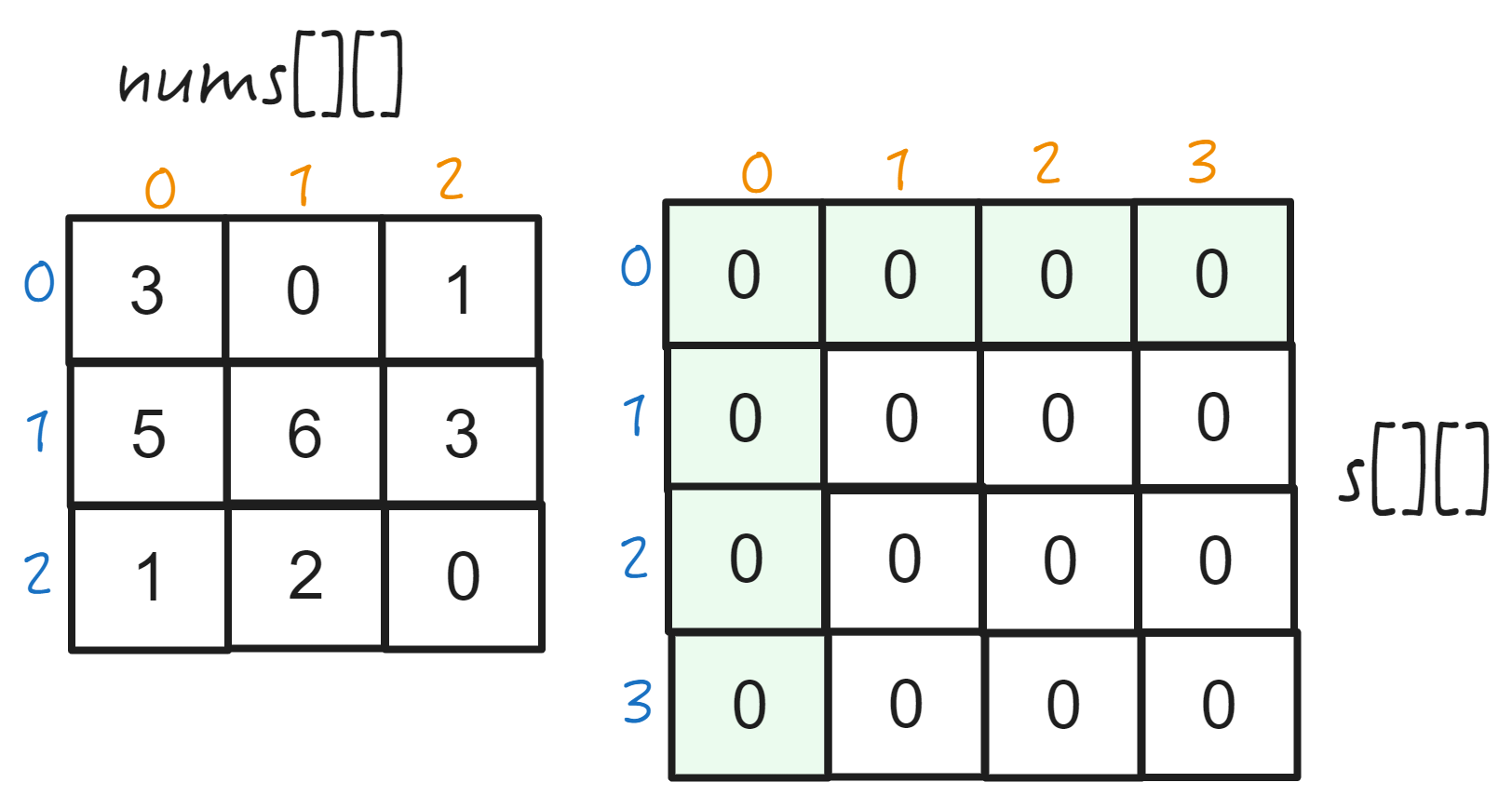
二维数组的前缀和 S[X][Y] = nums[0][0] + ... nums[X-1][Y-1]

构建前缀和数组

假设原数组nums[m][n]，前缀和数组 S[m+1][n+1],预留第0行，第1列不用。

计算前缀和数组第一行S[0][Y]

前缀和的第一行即为原数组的第一行求和(类似一维数组求和)，初始化前缀和数组。

java 复制代码

S[0][y] = nums[0][0] + .... nums[0][y-1]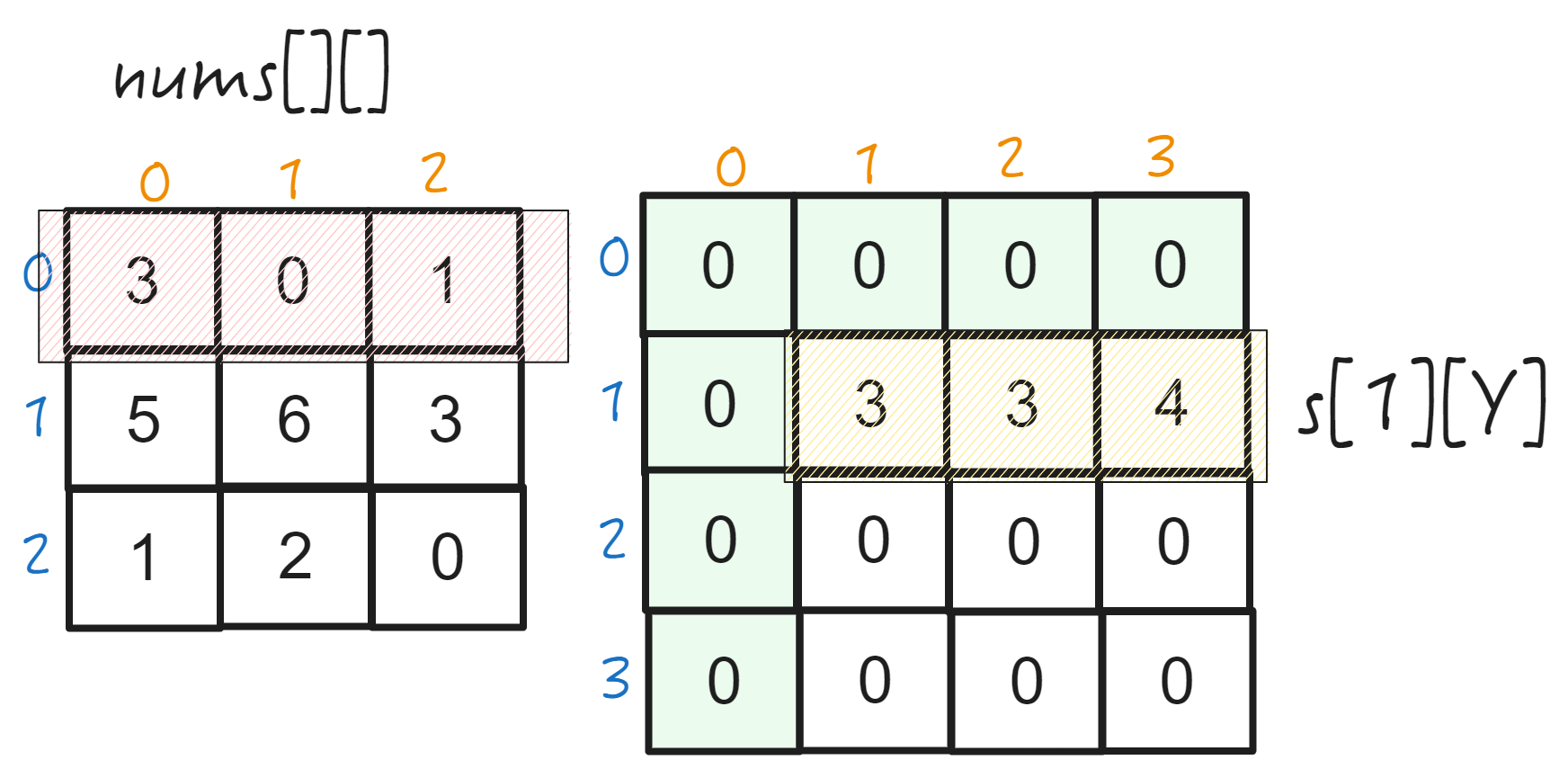

构建前缀和第二行

构建第三行

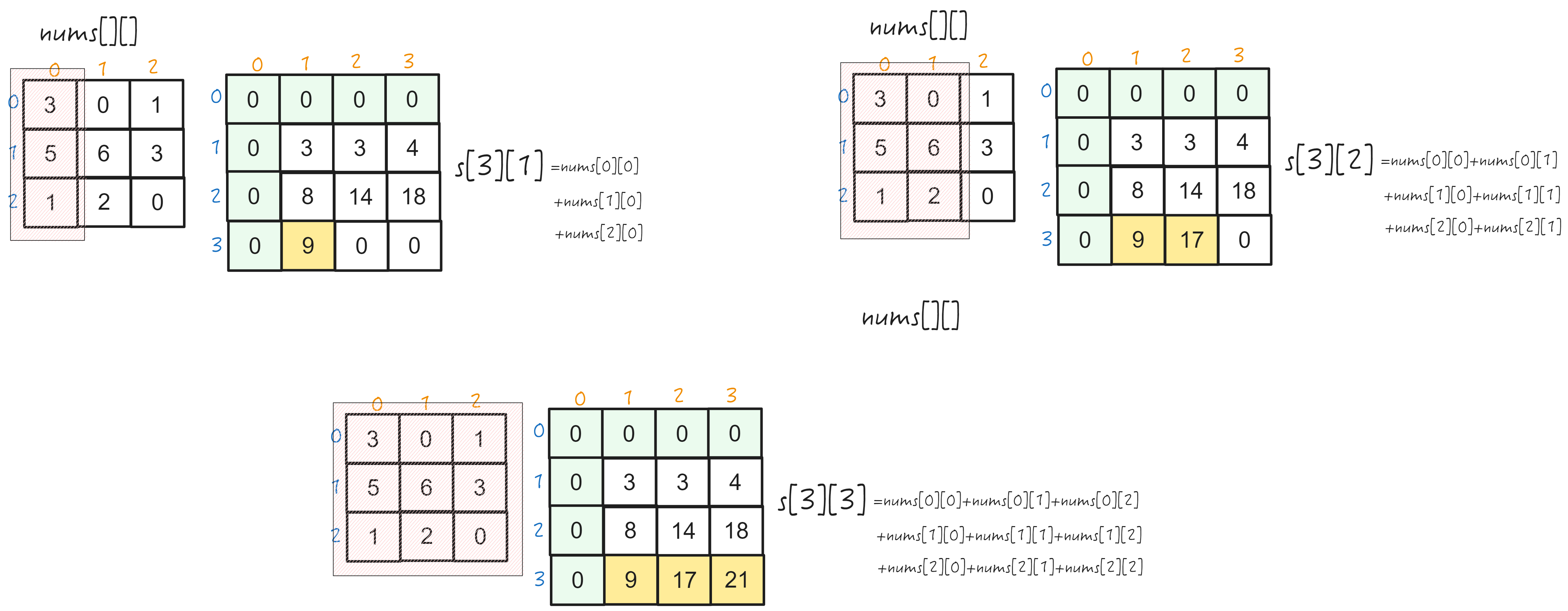
最终形态

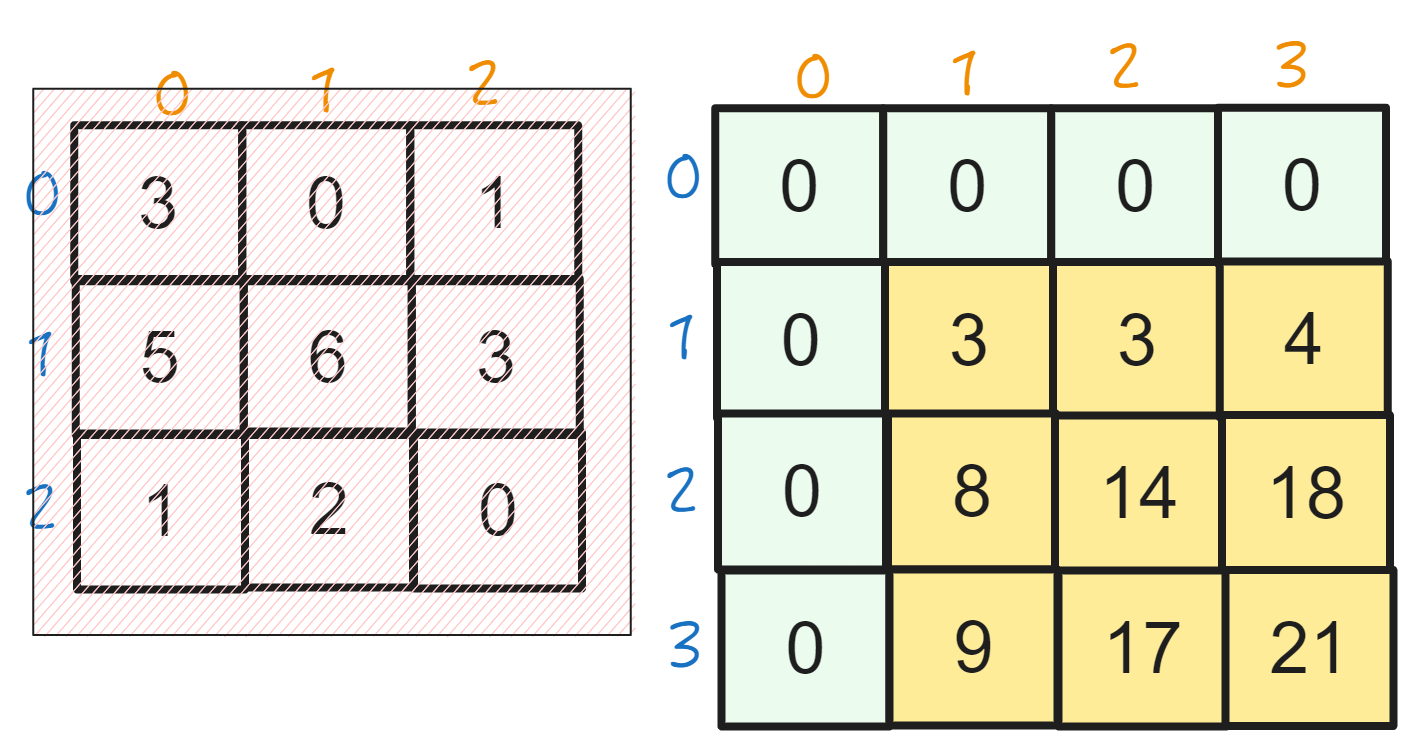
前项和公式

我们观察S[3][3]

java 复制代码

S[3][3] =  nums[0][0] + nums[0][1] + nums[0][2]
         + nums[1][0] + nums[1][1] + nums[1][2]
         + nums[2][0] + nums[2][1] + nums[2][2]
         
        =  nums[0][0] + nums[0][1] + nums[0][2] + nums[1][0] + nums[1][1] + nums[1][2]
         + nums[0][0] + nums[0][1] + nums[1][0] + nums[1][1] + nums[2][0] + nums[2][1]
         + nums[2][2] 
         - nums[0][0] - nums[0][1] - nums[1][0] - nums[1][1]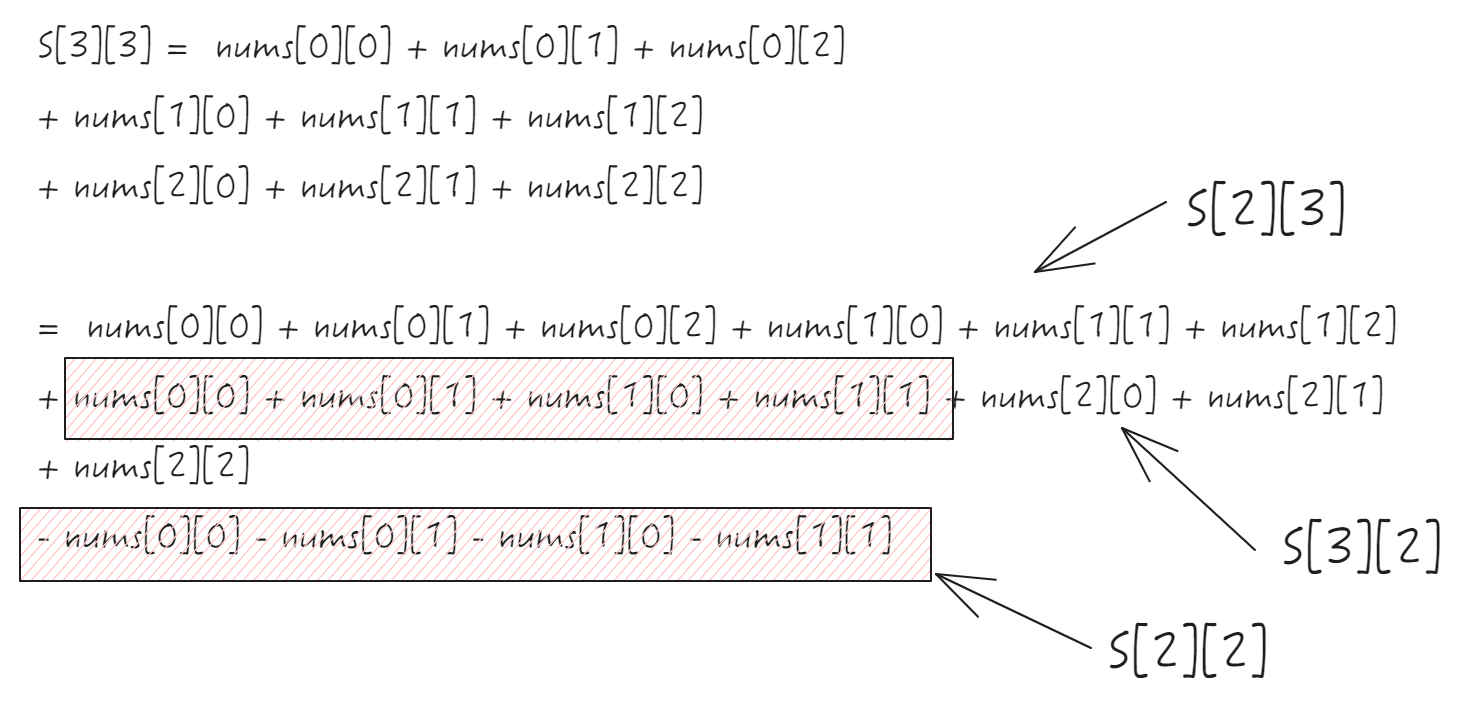

S[i , j] = S[i-1][j] + S[i][j-1] + nums[i][j] - S[i-1][j-1]

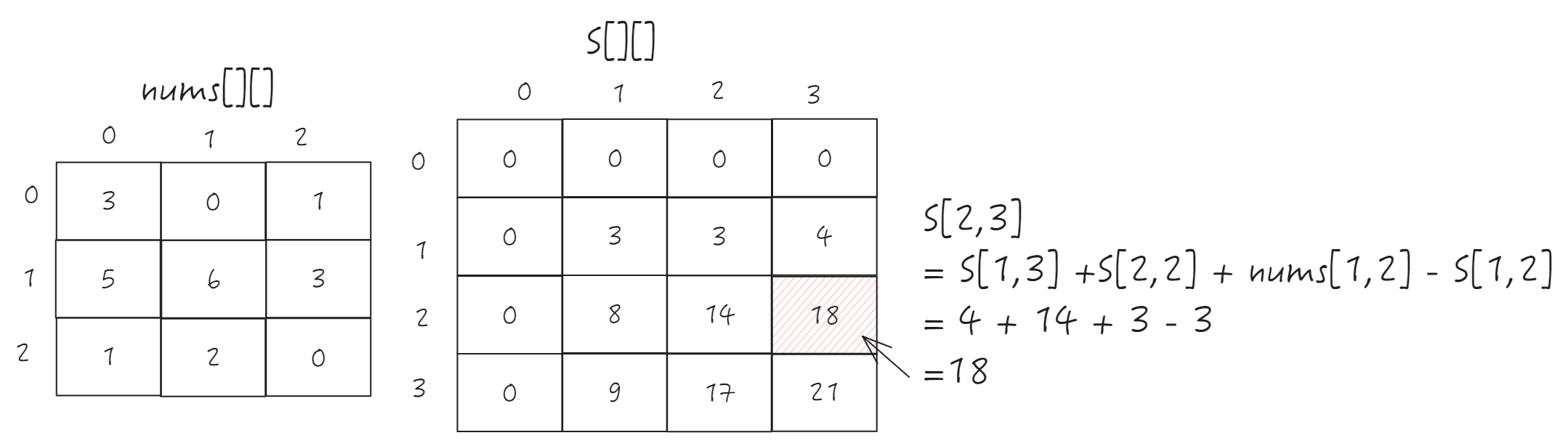
前缀和例题

二维区域和检索 - 矩阵不可变

问题

304. 二维区域和检索 - 矩阵不可变 - 力扣（LeetCode）

问题描述

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

示例 1：

java 复制代码

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

解决方案

构建前缀和

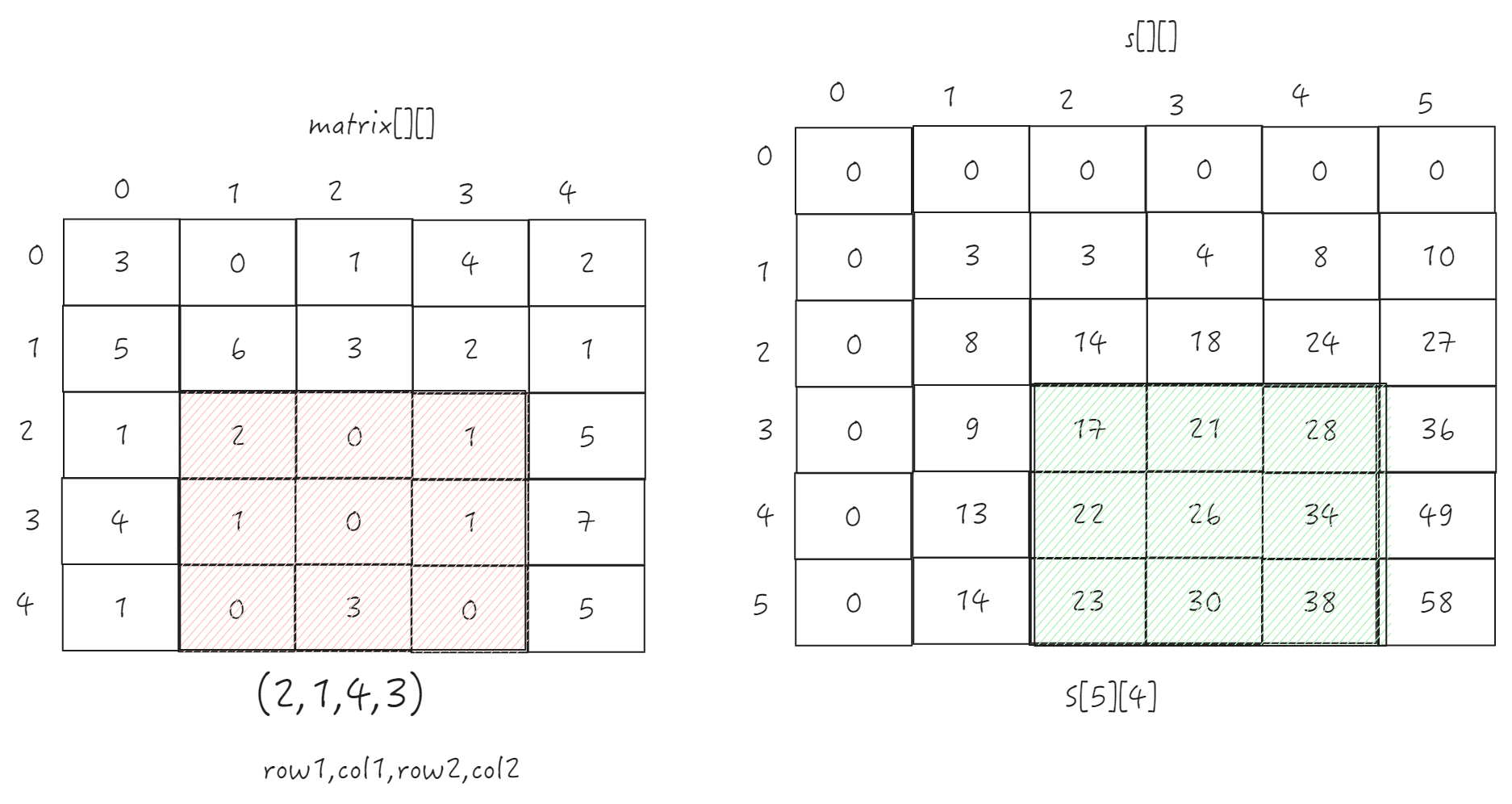
求阴影部分的值

由图我们观察到阴影部分的可以看做：（0,0）->((row2+1), (col2+1)) - （0,0）->((row1), (col2+1)

- （0,0）->((row2+1), (col1) + （0,0）->((row1), (col1) 【此矩形被减去了两次】

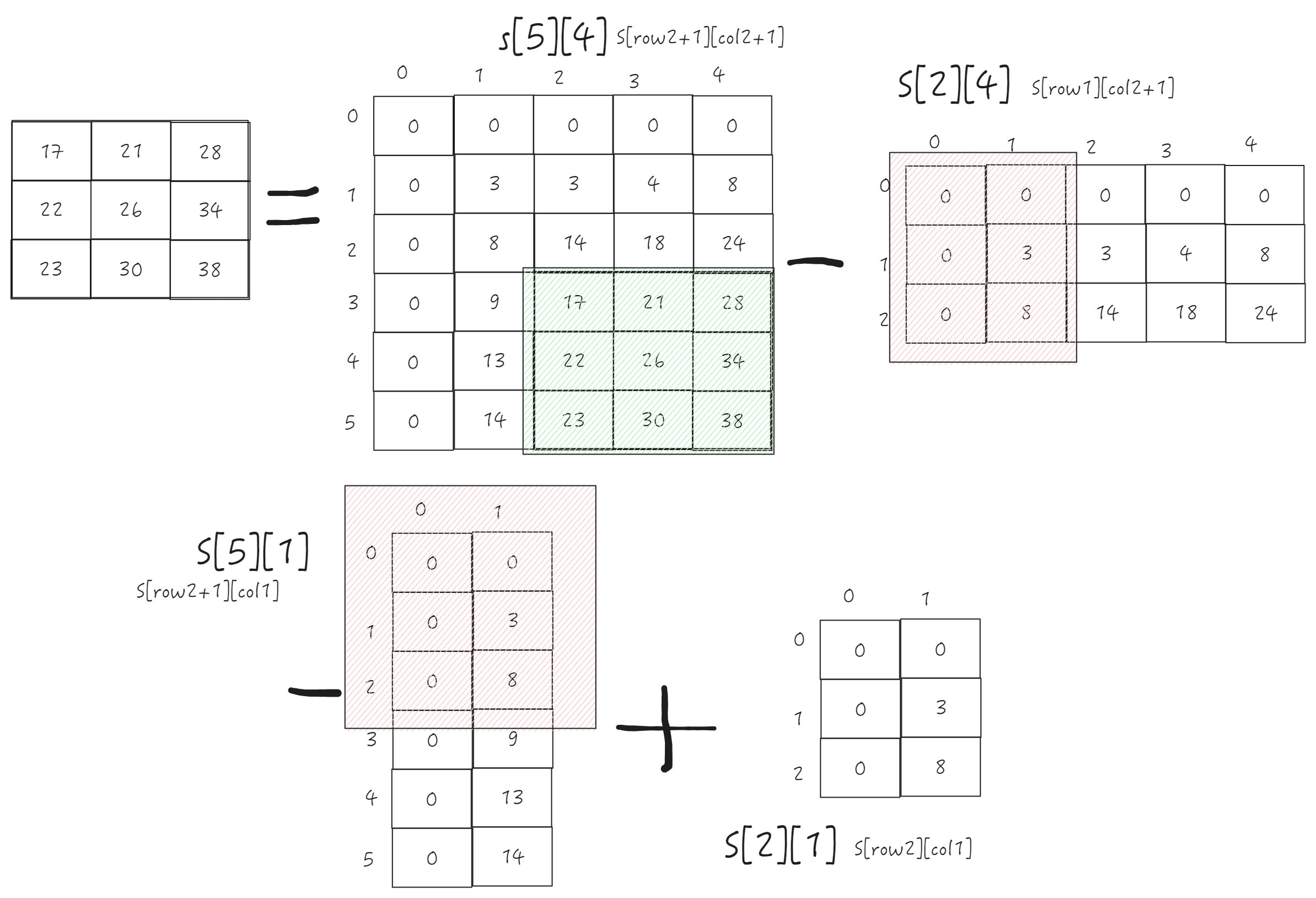
java 复制代码

s[row2+1][col2+1] - s[row1][col2+1] - s[row2+1][col1] + s[row1][col1];