大数据挖掘
数据挖掘
数据挖掘定义
技术层面:
数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据 中,提取隐含在其中、人们事先不知道的、但又==潜在有用的信息==的过程。
数据准备环节
数据选择 质量分析 数据预处理
数据仓库
从多个数据源搜集的信息存放在一致的模式之下
特征化
对目标数据的一般特性和特征汇总
聚类分析
最大化类内相似度 最小化类间相似性
数据准备
大数据定义
超出正常处理范围
由海量数据+复杂类型的数据 构成
数据对象
组成数据集的元素,每个数据对象均为一个实体
数据对象由属性描述
数据的正确性分析
缺失值
数据错误
度量标准错误
编码不一致
处理缺失数据
忽视
较小缺失率 有缺失值的样本或属性
人工补全缺失值
重新采样
领域知识
自动补全缺失值
固定值
均值
基于算法
插补法
均值插补
回归插补
极大似然估计
噪声过滤
回归法
均值平滑法
离群点分析
处理噪声数据
局部离群因子LOF计算
数据量
子集选择
数据量太大
减小时间复杂度
数据聚合
尺度变换
数据更稳定
调整类分布
不平衡数据
哈尔小波交换
通过调整分辨率
数据标准化
最小最大标准化
Z-score标准化
大数据挖掘与分析
邻近性
相似性和相异性统称为邻近性
数据矩阵
存放数据对象
相异性矩阵
存放数据对象的相异性值
二元属性邻近性
数值数据距离
闵可夫斯基距离
h=1 2 正无穷
维度诅咒
基于距离的聚类在高纬度下无效
在高维情况下 P(0,1)更有效
逆文档频率
IDF 或 Goodall度量
基本思路:
将基本词汇看做全部属性的集合
每个词频是属性的值
余弦度量
余弦相似度
逆文档频率 阻尼系数
累计距离矩阵(大概率)
计算等图
算法题目APRIORI
基本的Apriori算法
Apriori算法的基本思路是采用层次搜索的迭代方法,由候选(k-1)-项集来寻找候选k-项集,并逐一判断产生的候选k-项集是否是频繁的。
设C k 是长度为k的候选项集的集合,L k 是长度为k的频繁项集的集合。为了简单,设最小支持度阈值min_sup为最小元组数,即采用最小支持度计数。
输入:事务数据库D,最小支持度阈值min_sup。
输出:所有的频繁项集集合L。
方法:其过程描述如下:
通过扫描D得到1-频繁项集L1;
for (k=2;Lk-1!=Ф;k++)
{ Ck=由Lk-1通过连接运算产生的候选k-项集;
for (事务数据库D中的事务t)
{ 求Ck中包含在t中的所有候选k-项集的计数;
Lk={c | c∈Ck and c.sup_count≥min_sup};
//求Ck中满足min_sup的候选k-项集
}
}
return L=∪kLk;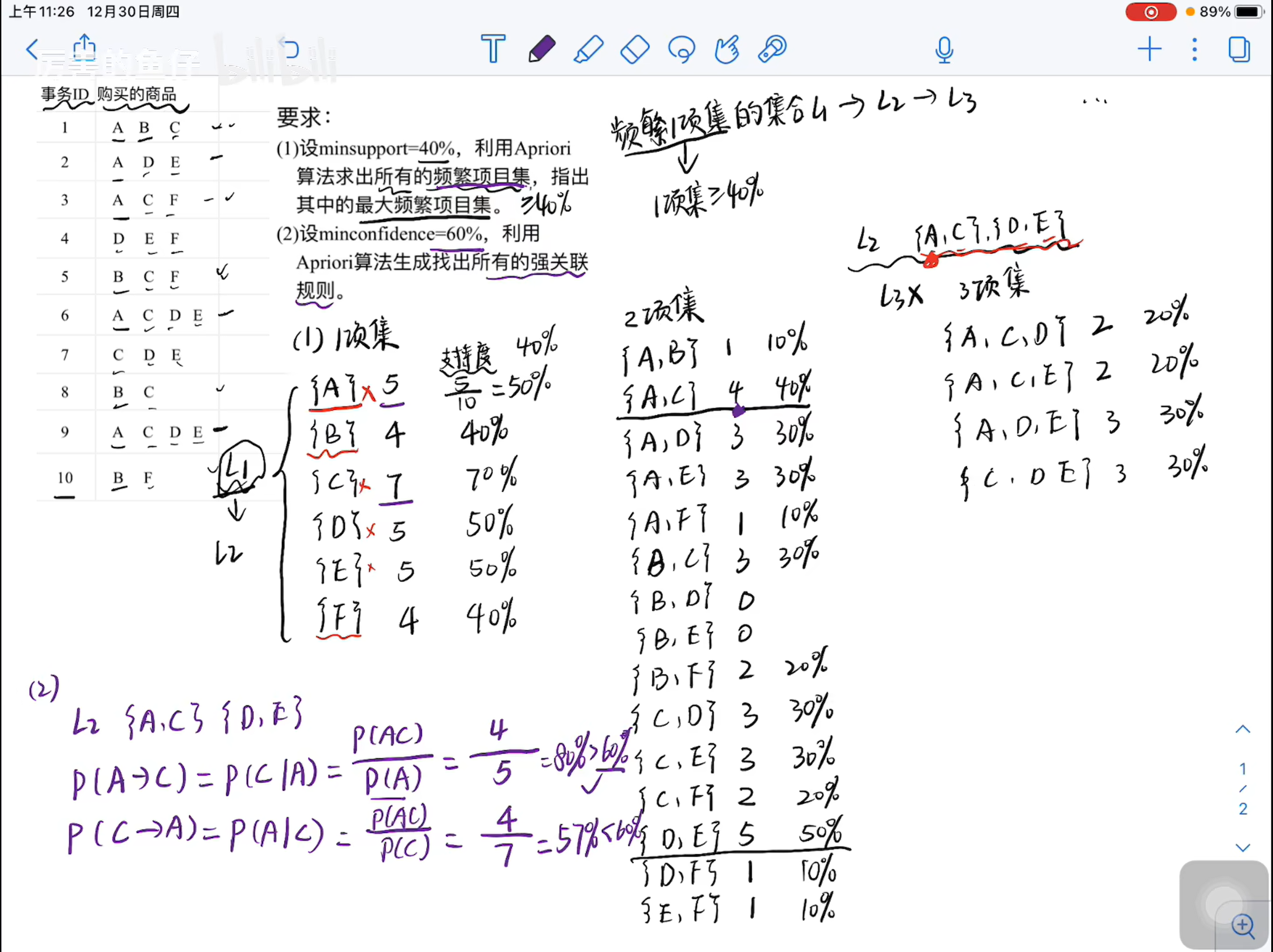
这是通过Apriori计算最大频繁项集 和 计算强关联规则的题目
要求为超过最小支持度 最小支持度的计算很简单
即为

算法题目FPgrowth

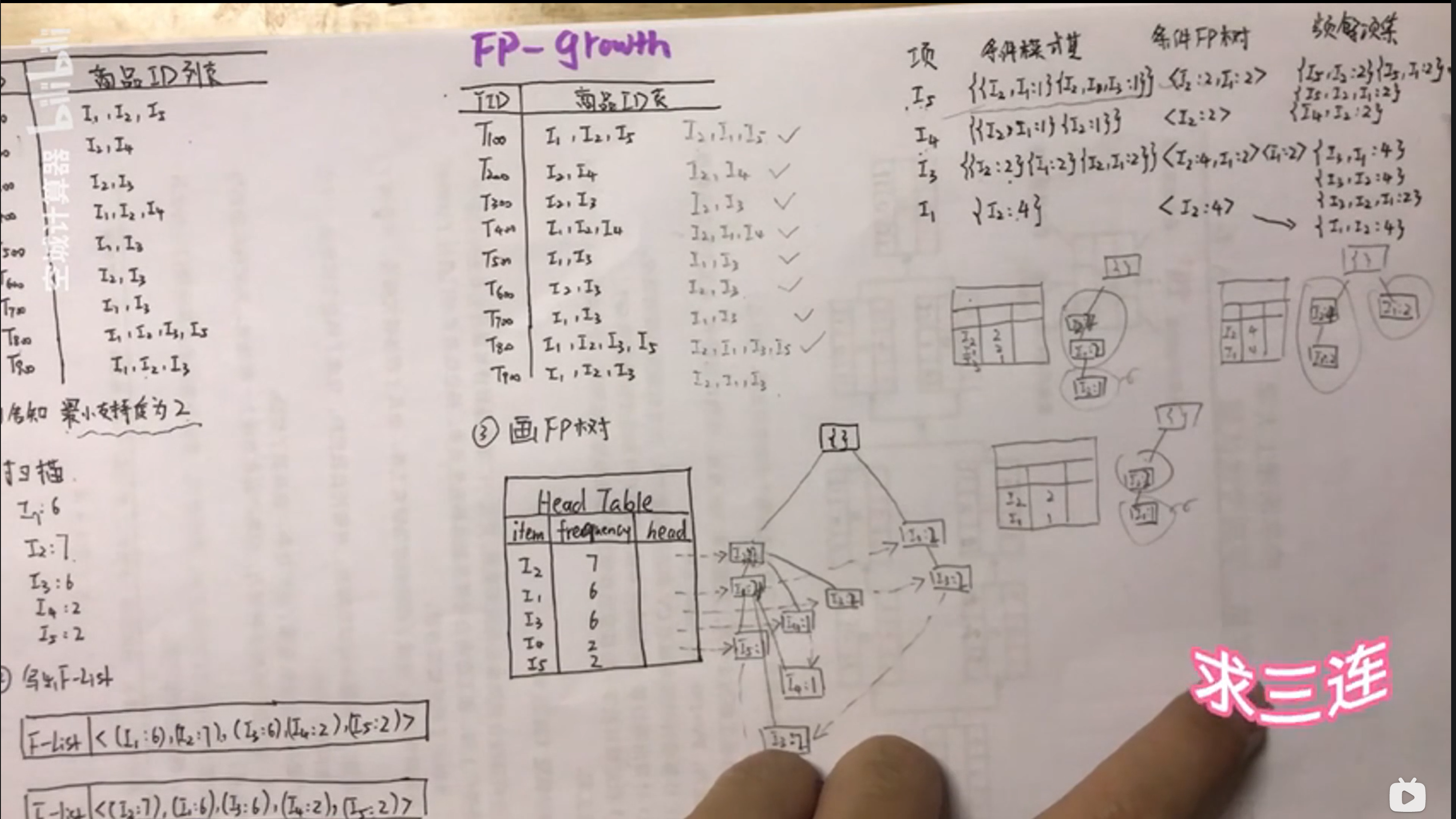
条件模式基的寻找
在FPtree的项目里倒着找,沿着虚线将出现的频次进行统计,,写出条件模式基
条件FP Tree
沿着条件模式基画FP Tree
记得剪去最小支持度不够的项
频繁项集
将条件FPtree与项进行组合 得到频繁项集
列式计数Apriori算法
使用垂直数据格式挖掘频繁项集
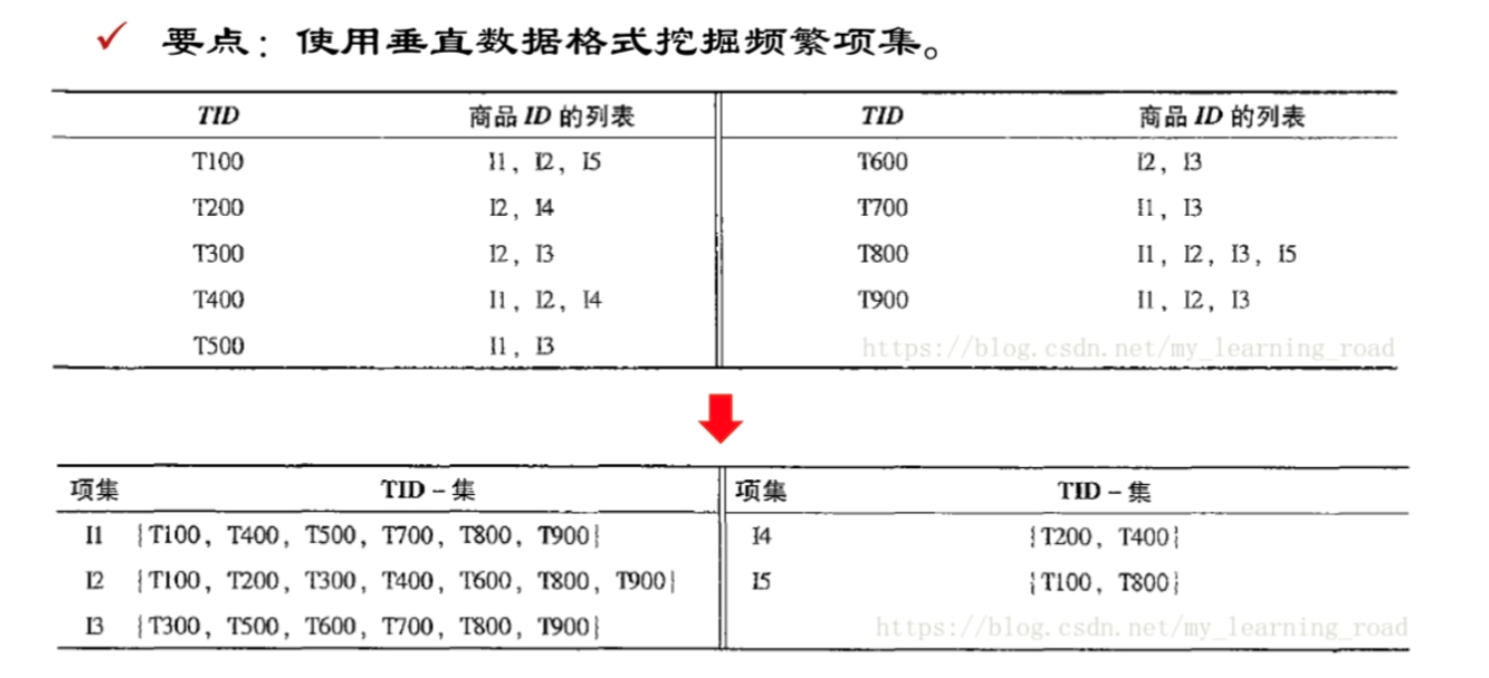
关联模式挖掘
超集
包含了另一个集合中所有元素的集合为超集
闭模式
一个频繁项集 没有任何它的超集具有与他相同的支持度
也就是不被冗余覆盖的核心模式
闭模式显著减少了需要存储的频繁模式数量
可以推导出所有频繁模式及其支持度
极大模式
没有频繁的超集
极大模式只保留频繁模式中"最大"的部分
无法还原所有频繁模式的支持度信息
提示:职业规划、创作规划等
Tips