注: 该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。
本期带来的是一篇改进的算法。作者在生长优化算法的基础上提出了一种集分布、对抗和平衡特征于一体的四参数自适应生长优化器(Quadruple parameter adaptation growth optimizer,QAGO)。在QAGO中,四参数自适应机制旨在降低算法对参数设置的敏感性,增强算法的自适应性。参数自适应机制采用遵循特定概率分布的参数抽样,实现算法超参数的动态调优。
该成果于2024年发表在计算机科学领域1区SCI期刊"Expert Systems with Applications"上,目前被引8次。

1.算法原理
一、首先介绍基本的生长优化算法原理:
(1)初始化
生长优化算法(GO)是一种基于种群的元启发式算法,它使用均匀分布在搜索空间中随机生成个体。详细的描述如以下公式所示:
其中,i为个体索引,j为个体Xi的维度索引,ub和lb分别为搜索空间的上界和下界。rand(0,1)生成一个随机数,该随机数在[0,1]范围内服从均匀分布。
(2)种群
标准GO使用超参数P1将总体划分为三层:顶层、中层和底层。顶层包含最优秀的个体Xbest和更优秀的个体Xbetter。底层包含最坏的个体Xworst。其余的正常个体Xnormal属于中等水平。所有的个体都根据他们的适合度从最好到最差排序。最优秀的个人的排名为1,而其他较好的个人的排名从2到P1。该算法将从一个特定的层面抽取个体来完成后续的计算。注意,整数P1在标准GO中被设置为5。
(3)学习阶段
GO的学习阶段模拟了个体在不同个体之间的差距中学习和成长的过程。在这个阶段,个体Xi将从差距中学习,并从中受益成长。这些差距包括四类:Gap1表示最优个体与较优个体之间的差距,Gap2表示最优个体与较差个体之间的差距,Gap3表示较优个体与较差个体之间的差距,Gap4表示随机两个不同于个体𝑋的个体之间的差距。用如下方式描述这些差距:
其中,Xbest、Xbetter、Xworse、Xr1、Xr2分别是由个体𝑋样本选择的最优个体、较优个体、较差个体和两个随机个体。
对于第k个gap(Gapk),个体的Xi序列将其转化为知识获取的kth组(KAk),并经历一个积累和演化的过程。在这个过程中,GO使用了自我感知因子(SF)和学习因子(LF)的概念来控制KA变量,这个过程将用方程描述如下:
其中SFi表示ith个体对自身状态的评估,LFk表示个体对外部状态的评估。在种群进化过程中,这两个控制参数通过方程自适应调整:
其中f(Xi)为ith个体的目标函数值,f(Xworst)为总体中最差个体的目标函数值。
其中,‖Gapk‖为kth组差距的欧几里得距离,LFk为归一化结果。
通过吸收不同个体之间的差距,ith个体完成了学习过程,用方程描述如下:
(4)反射阶段
GO的反射阶段模拟了个体的反思过程。在这个阶段,个体Xi通过三种不同的反射操作进一步成长。其具体过程通过方程描述如下:
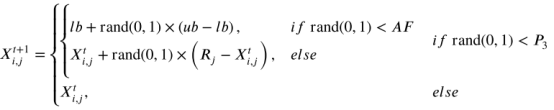
中R是一个比较好的P1随机个体。超参数P3控制执行不同操作的概率。注意,P3在标准GO中被设置为0.3。衰减因子控制重启操作,其数学模型由方程描述:
其中,FEs表示当前的评估次数,MaxFEs表示最大的评估次数。
(5)边界约束
在学习阶段和反射阶段,将使用以下边界约束方法来约束Xi中超出边界的某些变量。以下方程给出了其具体的数学模型:
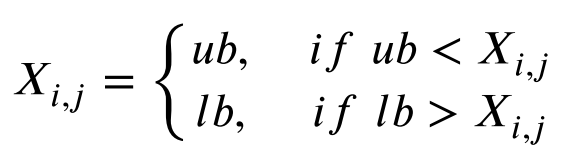
式中Xi,j表示个体Xi的j维度变量,如果它越过边界,则被限制在附近的边界。
(6)更新规则
GO的选择机制类似于模拟退火(SA)。两种方法都采用蒙特卡罗抽样的方法,以一定的概率保存演化失效的解。然而,GO使用固定的概率P2来保持劣解,而SA使用自适应方法。注意,在标准GO中,超参数2被设置为0.001。公式是GO更新规则的说明:
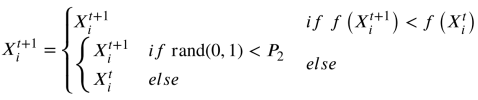
其中,f(x)是目标函数,它返回目标函数值。
二、四参数自适应生长优化器
在四参数自适应生长优化器算法中,设计了一个参数自适应机制,通过使用匹配特定分布的参数采样来实现算法超参数的动态调谐。该机制既保留了随机采样参数的简单性和多样性,又具有参数自适应机制的动态调谐特性。
因此,根据这一思想设计了动态参数P1,如等式所示:
其中,N是总体大小,rand(0.05,0.2)是服从[0.05,0.2]范围内均匀分布的随机数。下图显示了P1的采样过程。
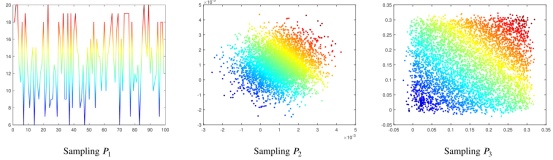
超参数P2表示保留未进化个体的概率。在GO中,使用固定参数P2来概率保留这些个体,既避免了计算资源的浪费,又使算法具有摆脱局部最优的能力。本研究采用高斯分布调整P2,其均值和标准差均基于GO中P2的设置,均为0.001。以下方程描述了这个设置:
超参数P3控制着使用不同计算方法的概率。GO中固定的P3可能会妨碍算法进行局部搜索的能力,因为它经常改变更多的维数。相比之下,QAGO算法使用较小的参数值来提高算法的局部搜索能力。然而,由于该算法无法确定最优参数值,因此它利用高斯分布来调整3,并获得近似最优参数配置。高斯分布的中心可以在[0,0.3]范围内的任何位置处生成。公式描述了其具体的数学模型:
其中,rand(0,0.3)是在[0,0.3]范围内服从均匀分布的随机数。对于单个Xi个体的每个维度j都有一个对应的P3。
(1) 基于对抗与平衡的三参数自适应
GO学习阶段的学习算子通过累积间隙来完成个体搜索方向的逼近过程。然而,在标准GO中从未使用过正常个体的信息。因此,表示问题空间的某些信息可能会丢失。因此,在QAGO算法中对间隙的计算方法进行了改进。每个个体都有可能参与计算过程,以确保全局最优区域周围的某些信息不会丢失。在每个间隙中,相邻等级的个体总是参与操作,为群体提供不同的进化信息。特别是后两个间隙不遵循这一规律,为演化提供了不确定的扰动。具体来说,QAGO的学习算子利用了五个间隙,旨在近似适应度景观。以下方程描述了所涉及的差距:
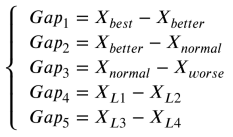
其中L1、L2、L3和L4是不同于i的单个索引。
(2) 基于一维向量映射的参数自适应
一维映射可以通过将高维向量映射到一维空间来简化高维向量的表示和处理。这降低了计算复杂度和内存使用,最终提高了算法效率。因此,我们将这一思想应用于参数自适应。该方法涉及到两个向量的一维映射,并将其应用于LFk的自适应过程中。方程描述了Gapk中成对向量的映射过程:
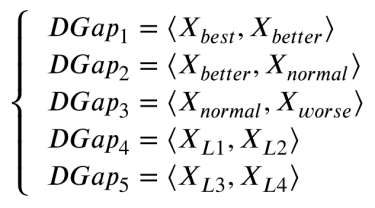
其中DGapk是Gapk里两个向量的一维映射值,而<Xbest,Xbetter>表示内积操作。
为了避免极小的正值和零,将所有值移动2 |min(DGap)|。因此,LFk根据公式计算:
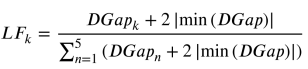
其中min为求最小值的函数,n和k均为Gap的索引,k∈[1,2,3,4,5]。
(3) 基于适应度差的参数自适应
在标准GO中,只考虑个体Xi和最差个体来适应SFi。针对该问题,设计了一种新的自适应算法,该算法考虑了两个向量之间的适应度差异Gapk。如果两个向量之间的适应度差异较大,则认为它们提供了全局信息,以促进个体的全局探索。相反,如果两个向量之间的适应度差异很小,它们被认为是提供局部信息,以促进个体的局部利用。
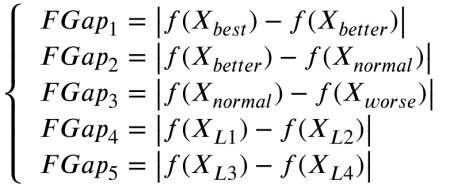
式中 为两个体间适应度差绝对值。此外,为了更好地完成SF的自适应过程,对所有的FGap值进行了归一化。方程描述了SFk受影响的过程:
其中SFk为Gapk的自适应缩放参数。
(4)基于Jensen-Shannon散度的参数自适应
在QAGO中,L和S的设计似乎是一种"矛与盾"的关系。这些矛盾既相互依存又相互制约。然而,矛盾也是事物发展的动力。
在信息论中,Jensen-Shannon散度的平方根是两个概率函数之间距离的度量。实际上,归一化的LF和SF似乎类似于两个系统或概率分布。因此,在参数自适应机制中引入Jensen-Shannon散度的概念,以观察和估计两个系统之间的距离,更好地平衡QAGO中学习算子的自适应过程。
使用方程计算LF和SF系统之间的距离,即距离dJS,由下式计算:
其中, 是Jensen-Shannon散度。
(5)算子细化
在标准GO中,学习算子不使用正常个体,导致问题空间表示中的局部信息丢失。因此,重新定义了学习算子的结构,以便对种群进行更有效的进化。新的算子结构在方程中描述,使用基于对抗和平衡特征的三参数自适应方法来改进学习算子。
在计算了LF和SF之间的距离dJS之后,用它来平衡LF和SF的参数自适应过程。通过以上过程,学习算子得到了高度的自适应和充分的细化。方程说明了自适应规则改进学习算子的过程:
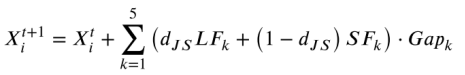
(6)反射算子细化
本文重新设计了反射阶段的反射算子,以改善QAGO算法过早收敛的可能性。以下公式给出了相应的数学模型:
其中Rj为精英R的jth维数,RMj为随机个体的jth维数。
(7)边界约束
在改进学习阶段,由于间隙的积累,很容易导致一些变量违反约束,从而在该维度上失去收敛方向。在这一阶段,将使用方程对一些变量进行校正:
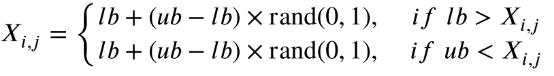
在改进反思阶段,个体的不同维度可能受到不同精英的指导。因此,在此阶段,使用方程来保持变量变化的趋势更有利于算法的收敛性。相关数学模型描述如下:
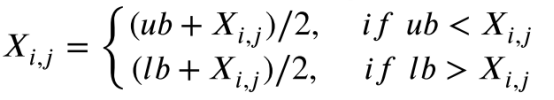
QAGO算法的伪代码如下所示:

QAGO算法的流程图如下所示:
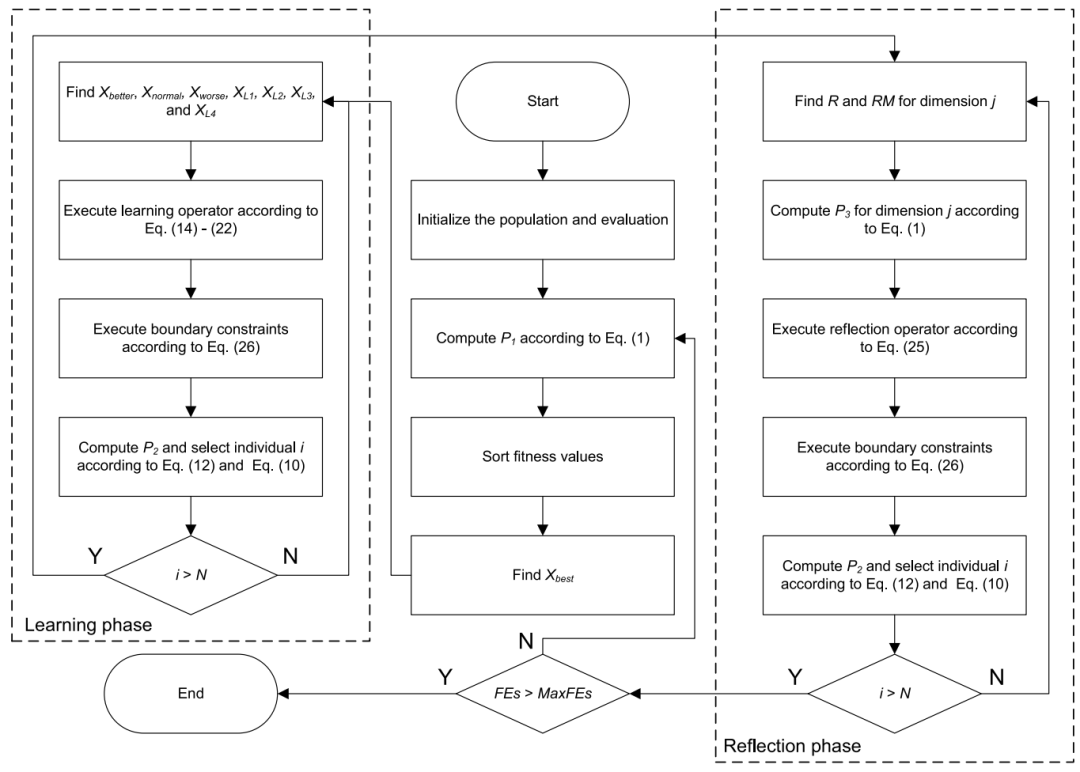
2.结果展示
采用作者独创的智能优化算法APP轻松对比一下本期算法。
例如在CEC2017函数集上,将QAGO算法与GO算法、SSA算法、PSO算法进行对比,结果如下:
F1函数:
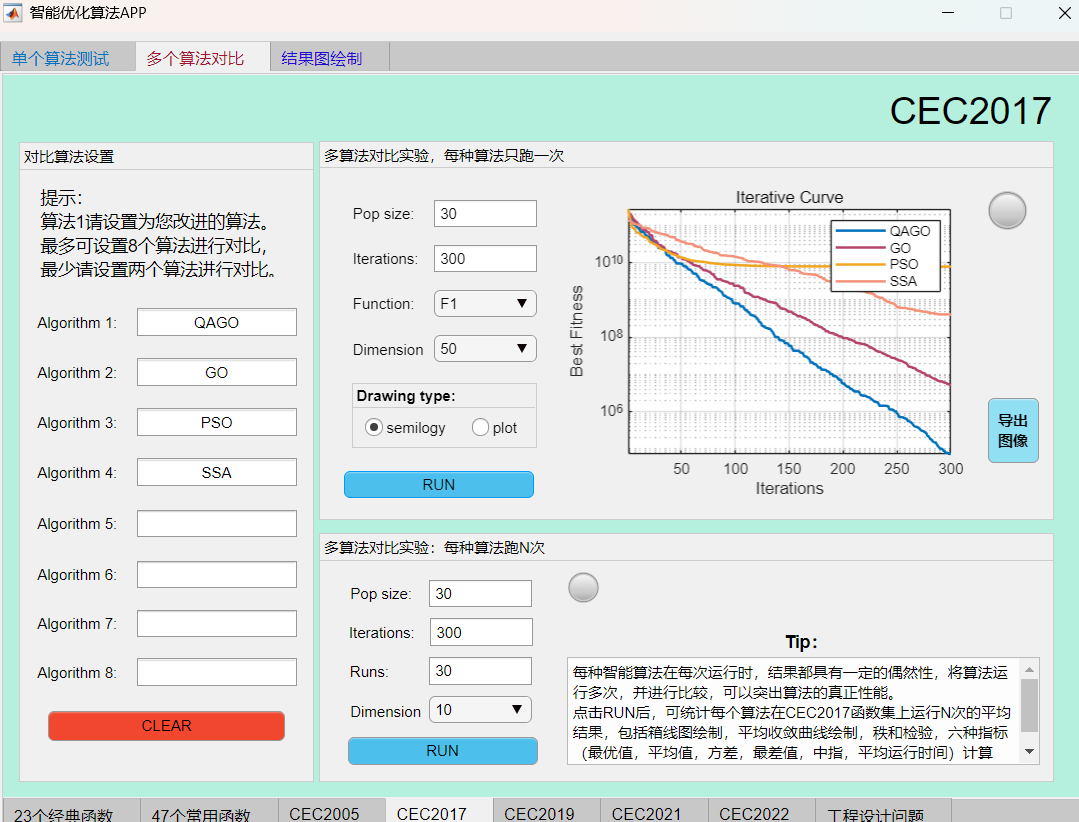
F4函数:
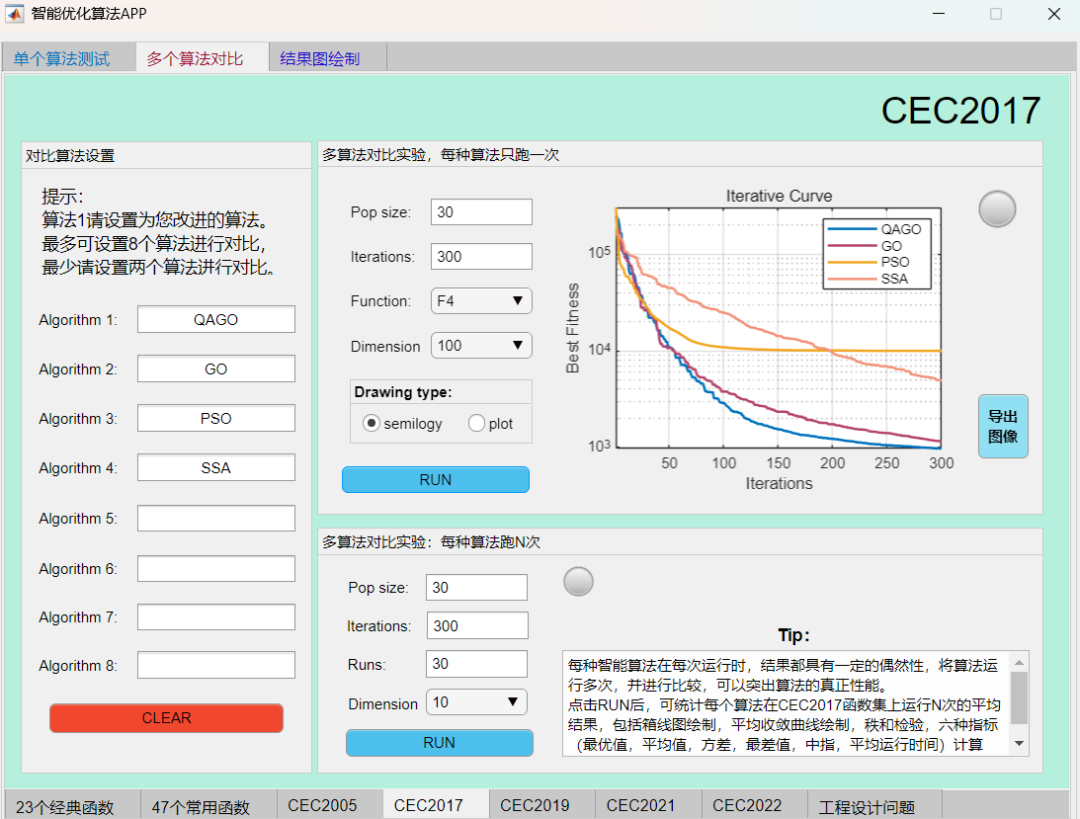
F7函数:
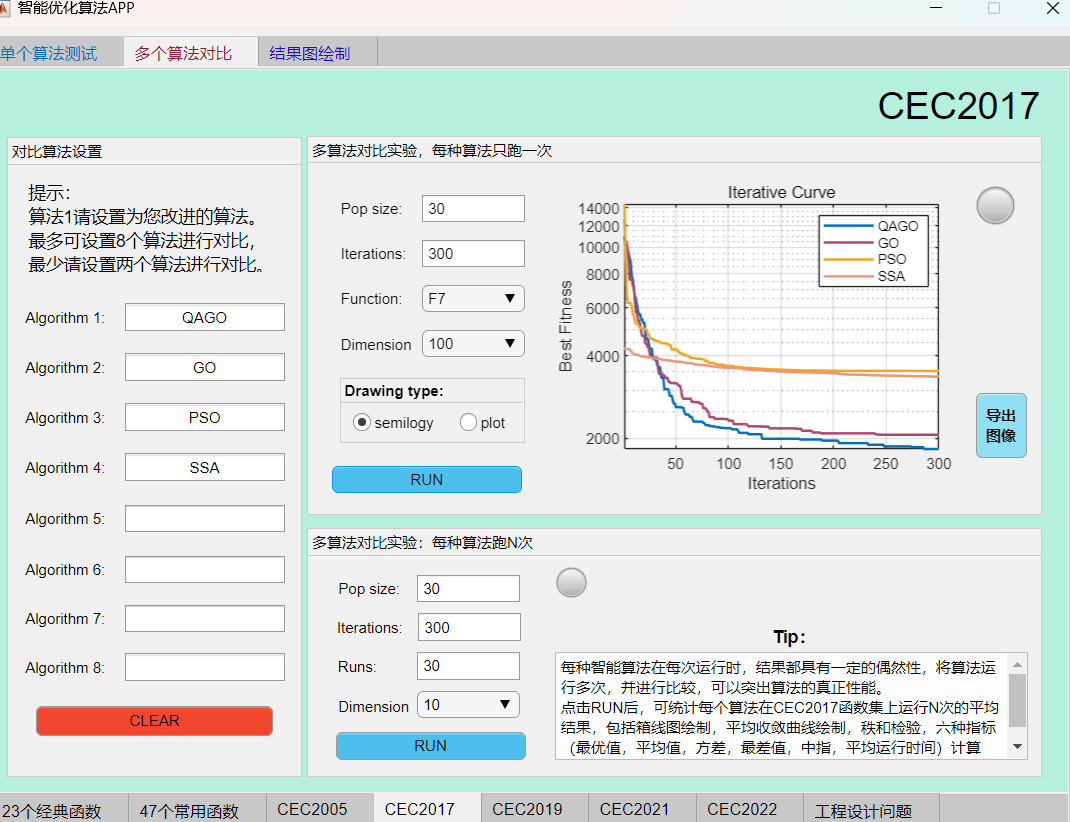
F11函数:
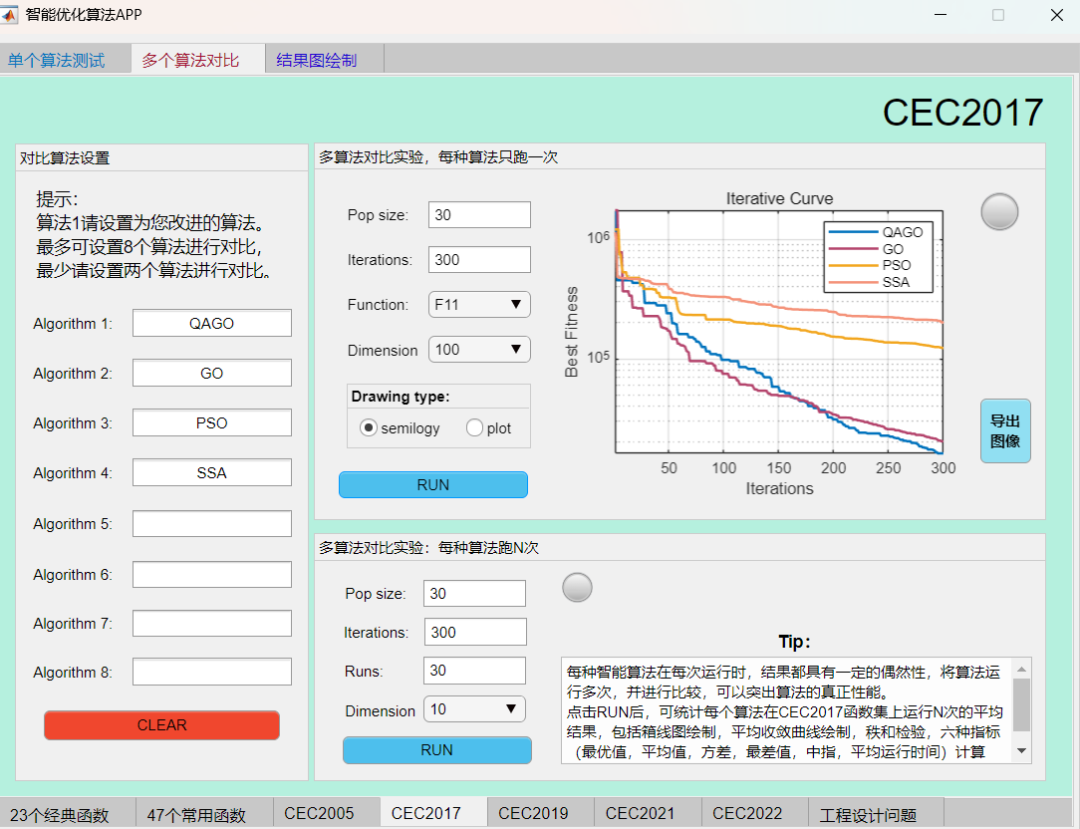
可见本期推出的QAGO算法在CEC2017函数集上,性能基本超越了经典的麻雀算法和粒子群算法。
3.MATLAB核心代码
perl
%微信公众号搜索:淘个代码,获取更多免费代码
%唯一官方店铺:https://mbd.pub/o/author-amqYmHBs/work
%代码清单:https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu
function [gbestfitness,gbestX,gbesthistory]= QAGO(N,MaxFEs,lb,ub,D,Func)
%---------------------------------------------------------------------------
% Algorithm Name: QAGO
% gbestx: The global best solution ( gbestx = [x1,x2,...,xD]).
% gbestfitness: Record the fitness value of global best individual.
% gbesthistory: Record the history of changes in the global optimal fitness.
%---------------------------------------------------------------------------
%% (1)Initialization
lb = lb.*(ones(1,D));
ub = ub.*(ones(1,D));
x=lb+(ub-lb).*rand(N,D);
gbestfitness=inf;
fitness=inf(N,1);
for i=1:N
fitness(i)=Func(x(i,:));
if gbestfitness>=fitness(i)
gbestfitness=fitness(i);
gbestX=x(i,:);
end
end
%% (2) Loop iteration
for it = 1:MaxFEs
[~, ind]=sort(fitness);
% Parameter adaptation based on distribution
P1=ceil(unifrnd(0.05,0.2)*N);
P2=normrnd(0.001*ones(1,N),0.001*ones(1,N));
P3=normrnd(0.3*rand(N,D),0.01);
%% 1. Improved learning phase
% Sampling individuals
Best_X=x(ind(1),:);
worse_index=ind(randi([N-P1+1,N],N,1));
Worst_X=x(worse_index,:);
better_index=ind(randi([2,P1],N,1));
Better_X=x(better_index,:);
normal_index=ind(randi([P1+1,N-P1],N,1));
Normal_X=x(normal_index,:);
[L1,L2,L3,L4]=selectID(N);
for i=1:N
Gap(1,:)=(Best_X-Better_X(i,:));
Gap(2,:)=(Better_X(i,:)-Normal_X(i,:));
Gap(3,:)=(Normal_X(i,:)-Worst_X(i,:));
Gap(4,:)=(x(L1(i),:)-x(L2(i),:));
Gap(5,:)=(x(L3(i),:)-x(L4(i),:));
% Parameter self-adaptation based on one-dimensional mapping of vectors
DGap(1,:)=(Best_X*Better_X(i,:)');
DGap(2,:)=(Better_X(i,:)*Normal_X(i,:)');
DGap(3,:)=(Normal_X(i,:)*Worst_X(i,:)');
DGap(4,:)=(x(L1(i),:)*x(L2(i),:)');
DGap(5,:)=(x(L3(i),:)*x(L4(i),:)');
minDistance=min(DGap);
DGap=DGap+2*abs(minDistance);
LF=DGap./sum(DGap);
% Parameter self-adaptation based on fitness difference
FGap(1,:)=(abs(fitness(ind(1))-fitness(better_index(i))));
FGap(2,:)=(abs(fitness(better_index(i))-fitness(normal_index(i))));
FGap(3,:)=(abs(normal_index(i)-fitness(worse_index(i))));
FGap(4,:)=(abs(fitness(L1(i))-fitness(L2(i))));
FGap(5,:)=(abs(fitness(L3(i))-fitness(L4(i))));
SF=FGap./sum(FGap);
% Parameter self-adaptation based on Jensen-Shannon divergence
LS=(LF+SF)/2;
Djs=0.5*sum(LF.*log(LF./LS))+0.5*sum(SF.*log(SF./LS));
djs=sqrt(Djs);
% Learning operator refinement
newx(i,:)=x(i,:)+sum(Gap.*(djs.*LF+(1-djs).*SF),1);
% Boundary constraints
Flag4ub=newx(i,:)>ub;
Flag4lb=newx(i,:)<lb;
newx(i,:)=(newx(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
% Evaluation
newfitness(i)=Func(newx(i,:));
% Selection
if fitness(i)>=newfitness(i)
fitness(i)=newfitness(i);
x(i,:)=newx(i,:);
if gbestfitness>=fitness(i)
gbestfitness=fitness(i);
gbestX=x(i,:);
end
else
if rand<P2(i)&&ind(i)~=ind(1)
fitness(i)=newfitness(i);
x(i,:)=newx(i,:);
end
end
end % end for
%% 2. Improved reflection phase
newx=x;
P2=normrnd(0.001*ones(1,N),0.001*ones(1,N));
VSCR=rand(N,D);
VSAF=rand(N,D);
AF=0.01*(1-it/MaxFEs);
I1=VSCR<P3;
I2=VSAF<AF;
R=ind(randi(P1,N,D));
for i=1:N
% Reflection operator refinement
for j=1:D
if I1(i,j)
if I2(i,j)
newx(i,j)=lb(j)+(ub(j)-lb(j))*rand;
else
S=randperm(N,3);
S(S==i)=[];
S(S==R(i,j))=[];
RM=S(1);
newx(i,j)=x(i,j)+rand*((x(R(i,j),j)-x(i,j))+(x(RM,j)-x(i,j)));
end
end
end
% Boundary constraints
Flag4ub=newx(i,:)>ub;
Flag4lb=newx(i,:)<lb;
newx(i,:)=(newx(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
% Evaluation
newfitness(i)=Func(newx(i,:));
% Selection
if fitness(i)>=newfitness(i)
fitness(i)=newfitness(i);
x(i,:)=newx(i,:);
if gbestfitness>=fitness(i)
gbestfitness=fitness(i);
gbestX=x(i,:);
end
else
if rand<P2(i)&&ind(i)~=ind(1)
fitness(i)=newfitness(i);
x(i,:)=newx(i,:);
end
end
end % end for
gbesthistory(it)=gbestfitness;
end % end while
end % end QAGO algorithm
%---------------------------------------------------------------------------
%Subfunction: Select four individuals different from Xi
function [L1,L2,L3,L4]=selectID(N)
for i=1:N
if 2 <= N
vecc=[1:i-1,i+1:N];
r=zeros(1,4);
for kkk =1:4
n = N-kkk;
t = randi(n,1,1);
r(kkk) = vecc(t);
vecc(t)=[];
end
L1(i)=r(1);L2(i)=r(2);L3(i)=r(3);L4(i)=r(4);
end
end
L1=L1';L2=L2';L3=L3';L4=L4';
end4.参考文献
Gao H, Zhang Q, Bu X, et al. Quadruple parameter adaptation growth optimizer with integrated distribution, confrontation, and balance features for optimization[J]. Expert Systems with Applications, 2024, 235: 121218.
完整代码获取
后台回复关键词:
TGDM823
获取更多代码:

javascript
或者复制链接跳转:
https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu