例题
例2-1 采用脉冲响应不变法设计一个巴特沃斯数字低通滤波器
要求:ωp=0.25π,Rp=1dB;ωs=0.4π,As=15dB,滤波器采样频率Fs=2000Hz。
matlab
wp=0.25*pi; %滤波器的通带截止频率
ws=0.4*pi; %滤波器的阻带截止频率
Rp=1;As=15; %滤波器的通带衰减指标和阻带衰减指标
ripple=10^(-Rp/20); %滤波器的通带衰减对应的幅度值
Attn=10^(-As/20); %滤波器的阻带衰减对应的幅度值
Fs=2000;T=1/Fs;Omgp=wp*Fs;Omg=ws*Fs;
%转变为模拟滤波器的技术指标
[n,Omgc]=buttord(Omgp,Omg,Rp,As,'s');
%模拟原型滤波器计算
[z0,p0,k0]=buttap(n);
%设计归一化的巴特沃斯模拟滤波器原型
ba1=k0*real(poly(z0));
%求原型滤波器的系数 b
aa1=real(poly(p0));
%求原型滤波器的系数 a
[ba,aa]=lp2lp(ba1,aa1,Omgc);
%变换为模拟低通滤波器
[bd,ad]=impinvar(ba,aa,Fs);
%用脉冲响应不变法计算数字滤波器系数
[H,w]=freqz(bd,ad);
%求数字系统的频率特性
dbH=20*log10((abs(H)+eps)/max(abs(H)));
subplot(2,2,1);plot(w/pi,abs(H));
ylabel('|H|');title('幅度响应');axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]);
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]);grid
subplot(2,2,2);plot(w/pi,angle(H)/pi);
ylabel('\phi');title('相位响应');axis([0,1,-1,1]);
set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]);
set(gca,'YTickMode','manual','YTick',[-1,0,1]);grid
subplot(2,2,3);plot(w/pi,dbH);
ylabel('幅度响应(dB)');title('幅度响应(dB)');
xlabel('频率(\pi)');axis([0,1,-40,5]);
set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]);
set(gca,'YTickMode','manual','YTick',[-50,-15,-1,0]);grid
subplot(2,2,4);zplane(bd,ad);axis([-1.1,1.1,-1.1,1.1]);title('零极点图');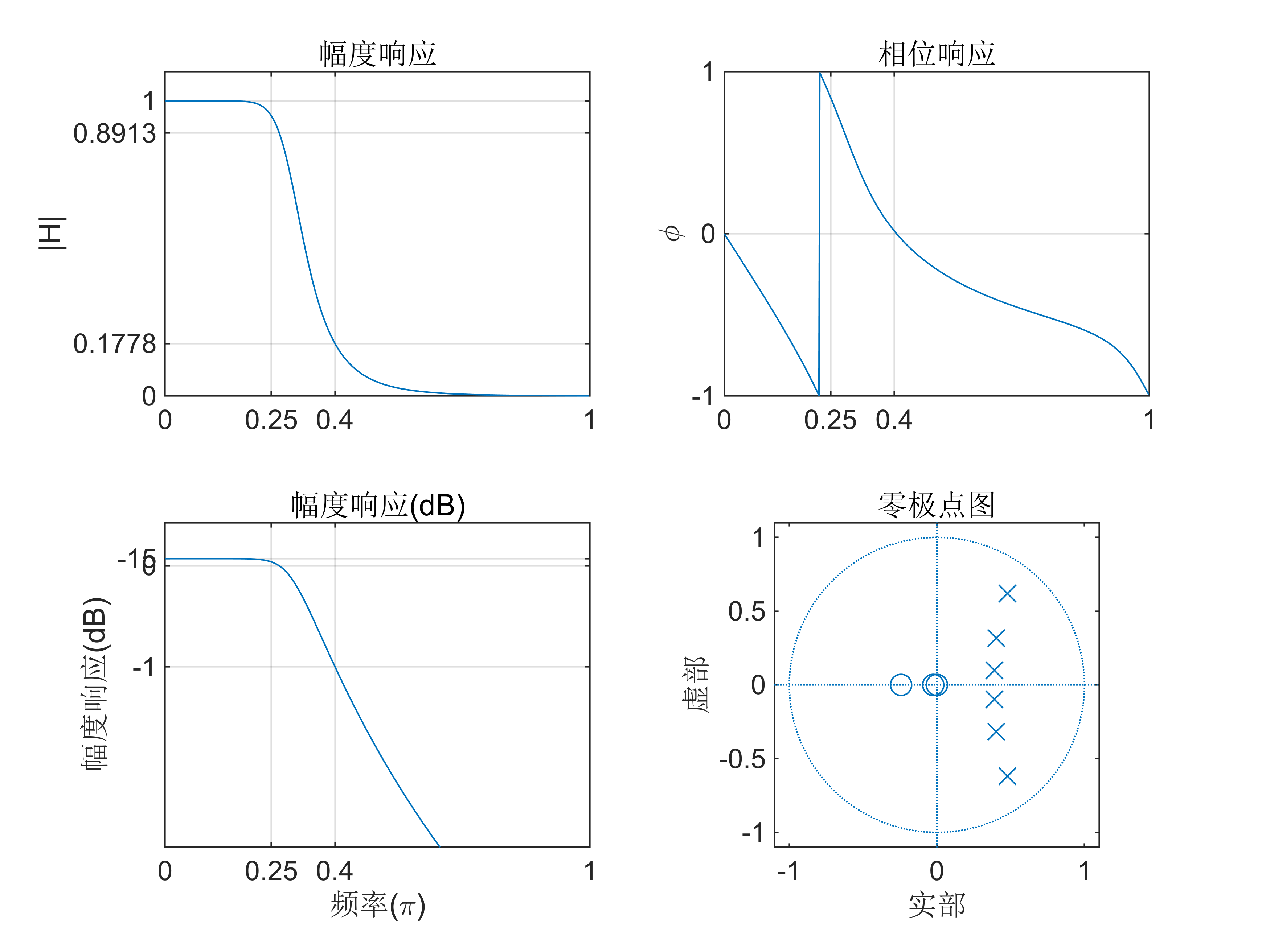
例2-2 设计一个巴特沃斯数字低通滤波器
要求 ωp=0.25π Rp=1dB ωs=0.4π As=15dB 滤波器采样频率 Fs=100Hz。
matlab
wp=0.25*pi; %滤波器的通带截止频率
ws=0.4*pi; %滤波器的阻带截止频率
Rp=1; As=15; %滤波器的通阻带衰减指标
ripple=10^(-Rp/20); %滤波器的通带衰减对应的幅度值
Attn=10^(-As/20); %滤波器的阻带衰减对应的幅度值
Fs=100; T=1/Fs;
Omgp=(2/T)*tan(wp/2); %原型通带频率的预修正
Omgs=(2/T)*tan(ws/2); %原型阻带频率的预修正
[n,Omgc]=buttord(Omgp,Omgs,Rp,As,'s'); %计算阶数n和截止频率
[z0,p0,k0]=buttap(n); %设计归一化的巴特沃思模拟滤波器原型
ba1=k0*real(poly(z0)); %求原型滤波器的系数 b
aa1=real(poly(p0)); %求原型滤波器的系数 a
[ba,aa]=lp2lp(ba1,aa1,Omgc); %变换为模拟低通滤波器
[bd,ad]=bilinear(ba,aa,Fs); %求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));
subplot(2,2,1); plot(w/pi,abs(H));
ylabel('|H|'); title('幅度响应'); axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]);
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]); grid
subplot(2,2,2); plot(w/pi,angle(H)/pi);
ylabel('\phi'); title('相位响应'); axis([0,1,-1,1]);
set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]);
set(gca,'YTickMode','manual','YTick',[-1,0,1]); grid
subplot(2,2,3); plot(w/pi,dbH); title('幅度响应(dB)');
ylabel('dB'); xlabel('频率(\pi)'); axis([0,1,-40,5]);
set(gca,'XTickMode','manual','XTick',[0,0.25,0.4,1]);
set(gca,'YTickMode','manual','YTick',[-50,-15,-1,0]); grid
subplot(2,2,4); zplane(bd,ad);
axis([-1.1,1.1,-1.1,1.1]); title('零极点图');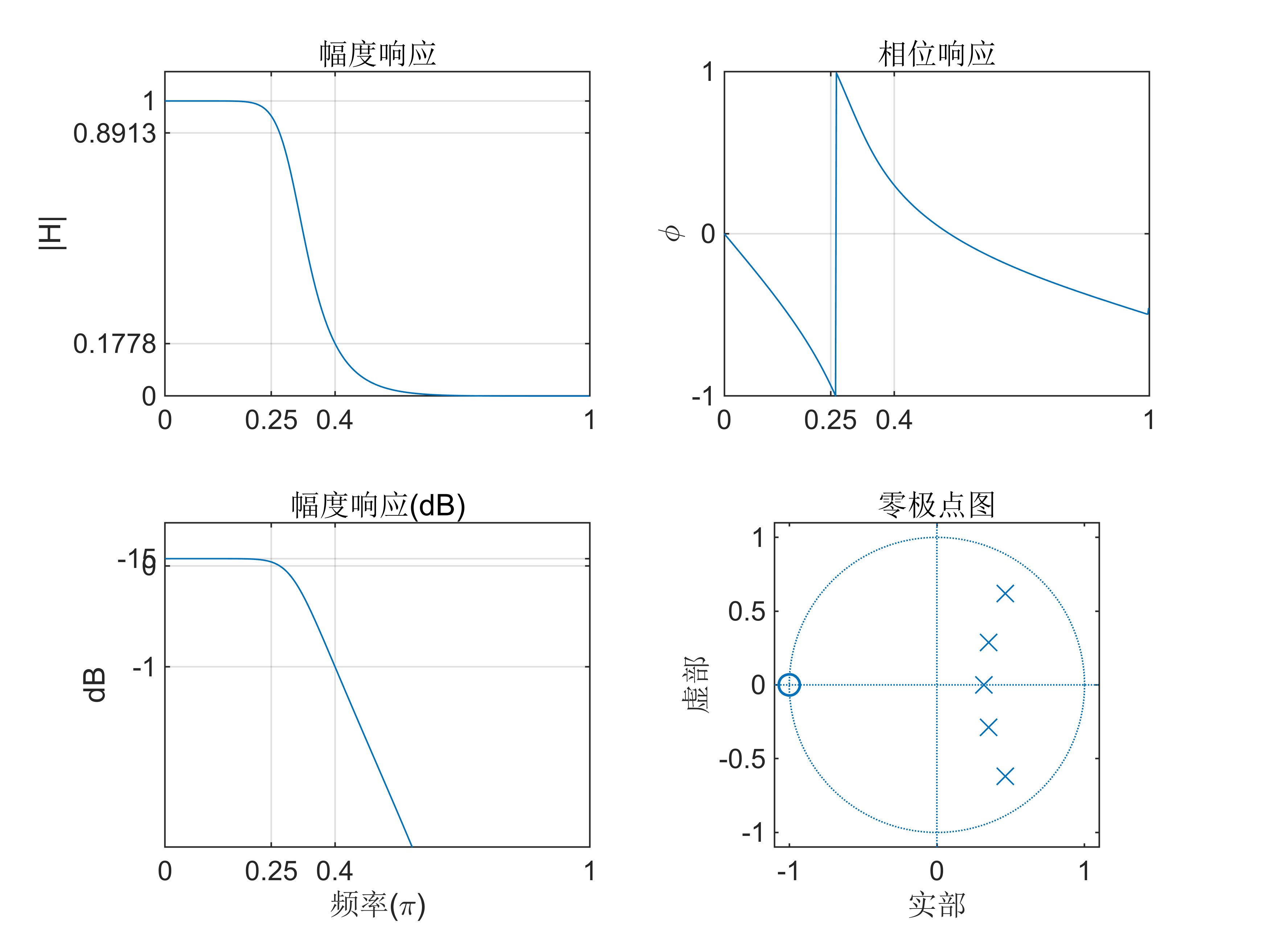
编写滤波器仿真程序,计算H(z)对心电图信号采样序列x(n)的响应序列y(n)。
matlab
xn=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];
B=[0.09036 0.09036*2 0.09036];
A=[1,-1.2686,0.7051];
yn=filter(B,A,xn);
figure;
subplot(2,1,1);
stem(0:length(xn)-1,xn,'.'); title('滤波前');
subplot(2,1,2);
stem(0:length(yn)-1,yn,'.'); title('滤波后');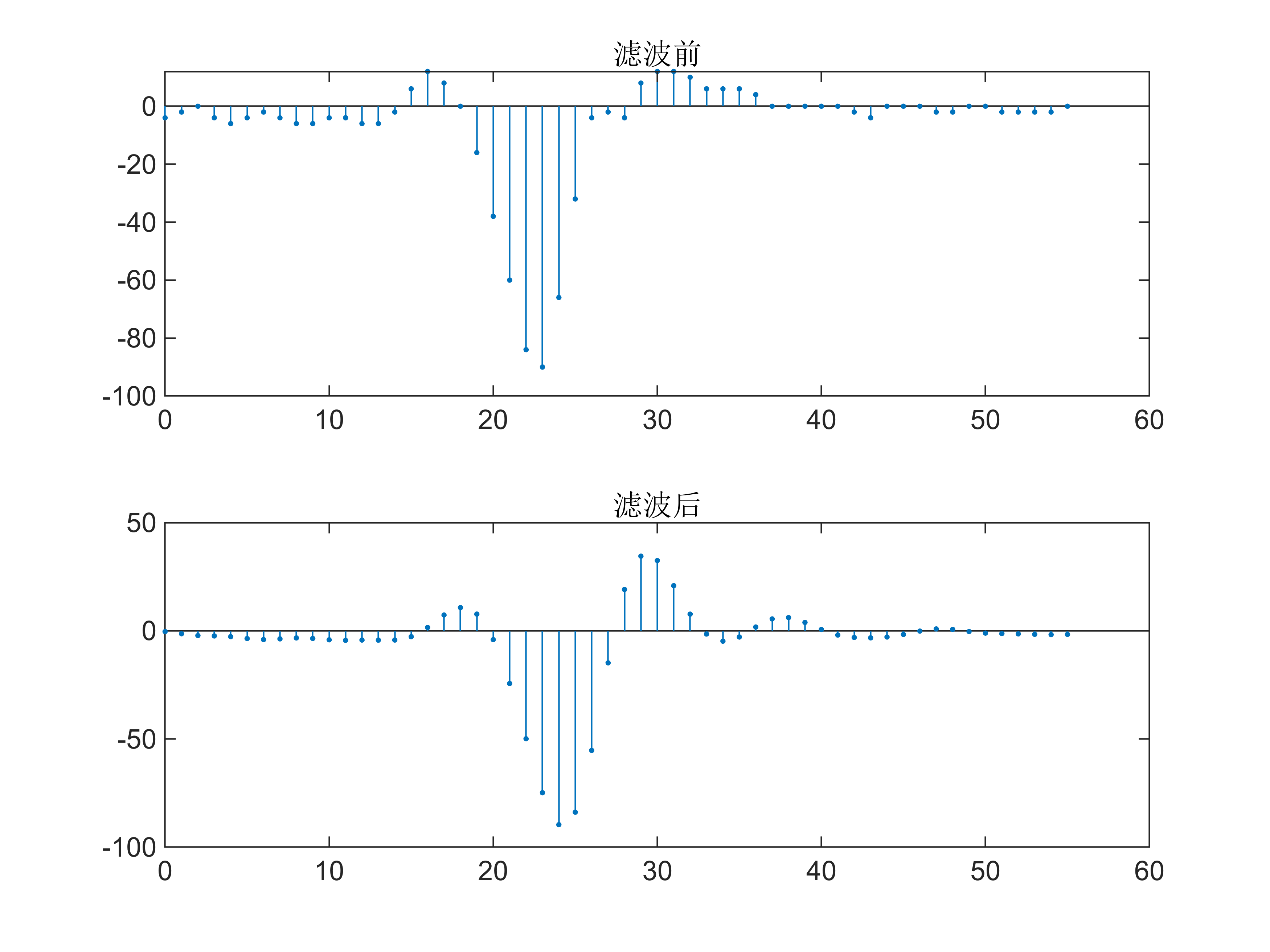
实验内容
1、 用双线性变换法设计的巴特沃斯数字低通滤波器
要求 ωp=0.2π Rp=1dB阻带 ωs=0.35π As=15dB 滤波器采样频率 Fs=10Hz。
matlab
close;clear;
wp=0.2*pi; %滤波器的通带截止频率
ws=0.35*pi; %滤波器的阻带截止频率
Rp=1; As=15; %滤波器的通阻带衰减指标
ripple=10^(-Rp/20); %滤波器的通带衰减对应的幅度值
Attn=10^(-As/20); %滤波器的阻带衰减对应的幅度值
Fs=10; T=1/Fs;
Omgp=(2/T)*tan(wp/2); %原型通带频率的预修正
Omgs=(2/T)*tan(ws/2); %原型阻带频率的预修正
[n,Omgc]=buttord(Omgp,Omgs,Rp,As,'s'); %计算阶数n和截止频率
[z0,p0,k0]=buttap(n); %设计归一化的巴特沃思模拟滤波器原型
ba1=k0*real(poly(z0)); %求原型滤波器的系数 b
aa1=real(poly(p0)); %求原型滤波器的系数 a
[ba,aa]=lp2lp(ba1,aa1,Omgc); %变换为模拟低通滤波器
[bd,ad]=bilinear(ba,aa,Fs); %求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));
subplot(2,2,1); plot(w/pi,abs(H));
ylabel('|H|'); title('幅度响应'); axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,1]);
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]); grid
subplot(2,2,2); plot(w/pi,angle(H)/pi);
ylabel('\phi'); title('相位响应'); axis([0,1,-1,1]);
set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,1]);
set(gca,'YTickMode','manual','YTick',[-1,0,1]); grid
subplot(2,2,3); plot(w/pi,dbH); title('幅度响应(dB)');
ylabel('dB'); xlabel('频率(\pi)'); axis([0,1,-40,5]);
set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,1]);
set(gca,'YTickMode','manual','YTick',[-50,-15,-1,0]); grid
subplot(2,2,4); zplane(bd,ad);
axis([-1.1,1.1,-1.1,1.1]); title('零极点图');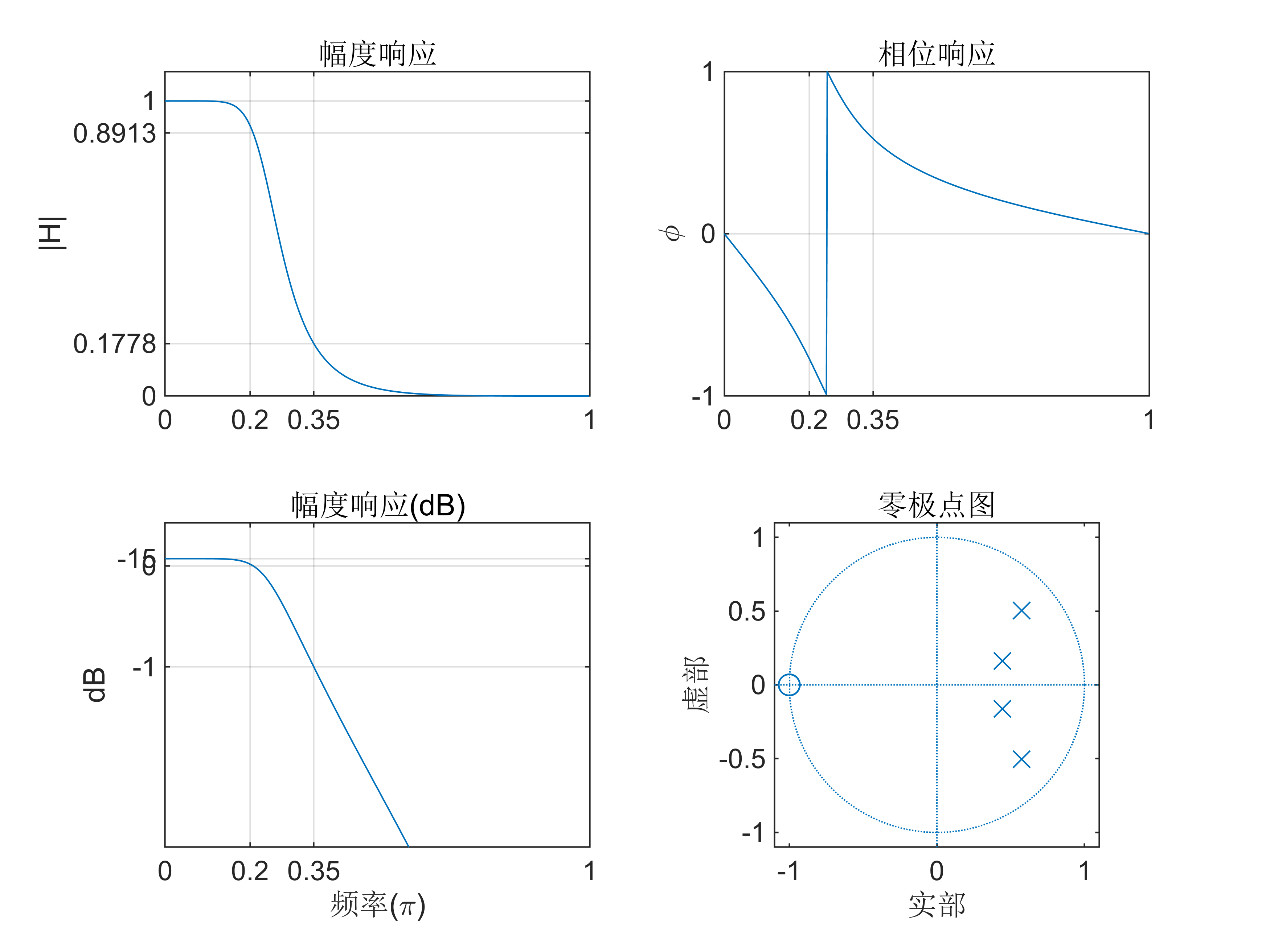
matlab
sys=tf(bd,ad,1/Fs)
matlabTextOutput
sys =
0.009163 z^4 + 0.03665 z^3 + 0.05498 z^2 + 0.03665 z + 0.009163
---------------------------------------------------------------
z^4 - 2.032 z^3 + 1.82 z^2 - 0.7706 z + 0.1294
采样时间: 0.1 seconds
离散时间传递函数。
模型属性2、用1 设计的数字滤波器对实际心电图信号采样序列(实验原理中已给出)进行滤波处理,分别绘制出滤波前后的心电图波形图和其幅频特性曲线,观察总结滤波作用与效果。
matlab
xn=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,...
-32,-4,-2,-4,8,12,12,10,6,6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];
yn=filter(bd,ad,xn);
Xw=fft(xn,1024);
Xw2=fft(yn,1024);
figure;
subplot(2,2,1);
stem(0:length(xn)-1,xn,'.'); title('滤波前');
subplot(2,2,3);
plot(linspace(0, 2, 1024),abs(Xw)); xlabel('\omega/\pi');
subplot(2,2,2);
stem(0:length(yn)-1,yn,'.'); title('滤波后');
subplot(2,2,4);
plot(linspace(0, 2, 1024),abs(Xw2)); xlabel('\omega/\pi');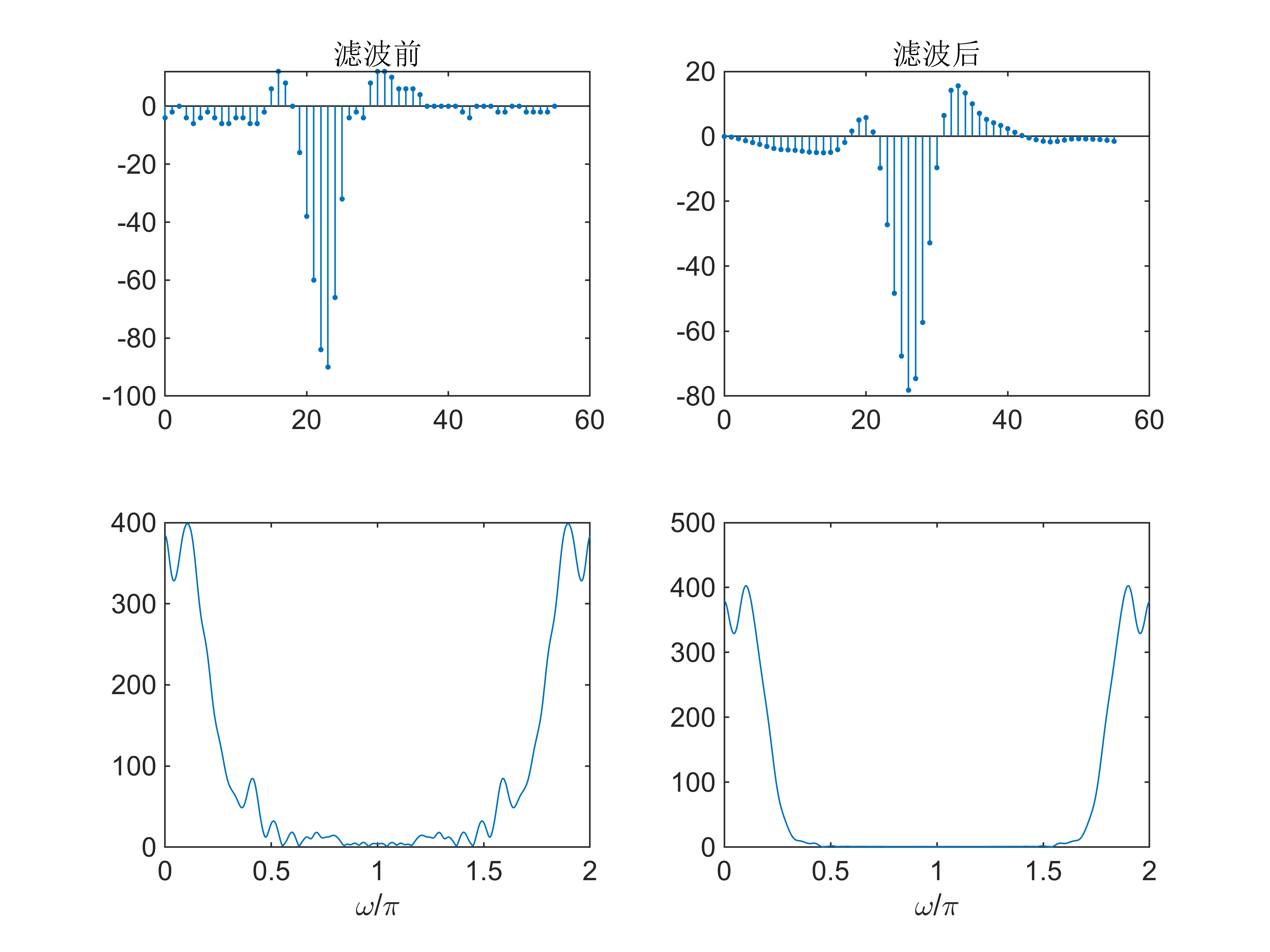
3、设计一个抗混叠低通滤波器(可在实验内容1 的代码上进行修改,截止频率的指标见2.6 节,衰减指标与实验内容1 一样)。
(1)读取音频信号motherland.wav,得到xn;
(2)对xn 进行D=2 的整数倍抽取,得到整数倍抽取后的音频信号yn1;
(3)对xn 先进行抗混叠滤波,再进行D=2 的整数倍抽取,得到音频信号yn2。
(1)音频播放:依次原始声音xn、没有经抗混叠滤波进行整数倍抽取的音频yn1、经过抗混叠滤波进行整数倍抽取的音频yn2,体验音频有频域混叠时的音质。
matlab
close;clear;
D=2;
[xn,fs] = audioread( ".\2024-2025(1)《信号处理实验》资料(请拷贝到u盘中,每次试验带到实验室)\实验中用到的一些函数和音频图像文件\motherland.wav");
sound(xn,fs);
pause(length(xn)/fs);% 播放音频信号,暂停执行程序 length(xn)/fs秒
yn1=xn(1:D:length(xn)); % 每个 D-1个点抽取 1点 ,这里 D=2
sound(yn1,fs/D); % 采用频谱降低到 fs/D(2) 取原音频 某 段信号,如 n=8000~8199。
画出 该段信号模拟域 幅度 谱 (横坐标为 f Hz);
画出该段信号 D=2抽取 后的 模拟域 幅度谱;
画出该段信号先经过抗混叠滤波再进行 D=2抽取的模拟域幅度谱。
matlab
close;
N=2048;
Xn=1/fs*fft(xn(8000:8199),N); % 从 xn中取 200点, N可取 2018
plot((0:N/2-1)*fs/N,abs(Xn(1:N/2))); % 模拟域幅度谱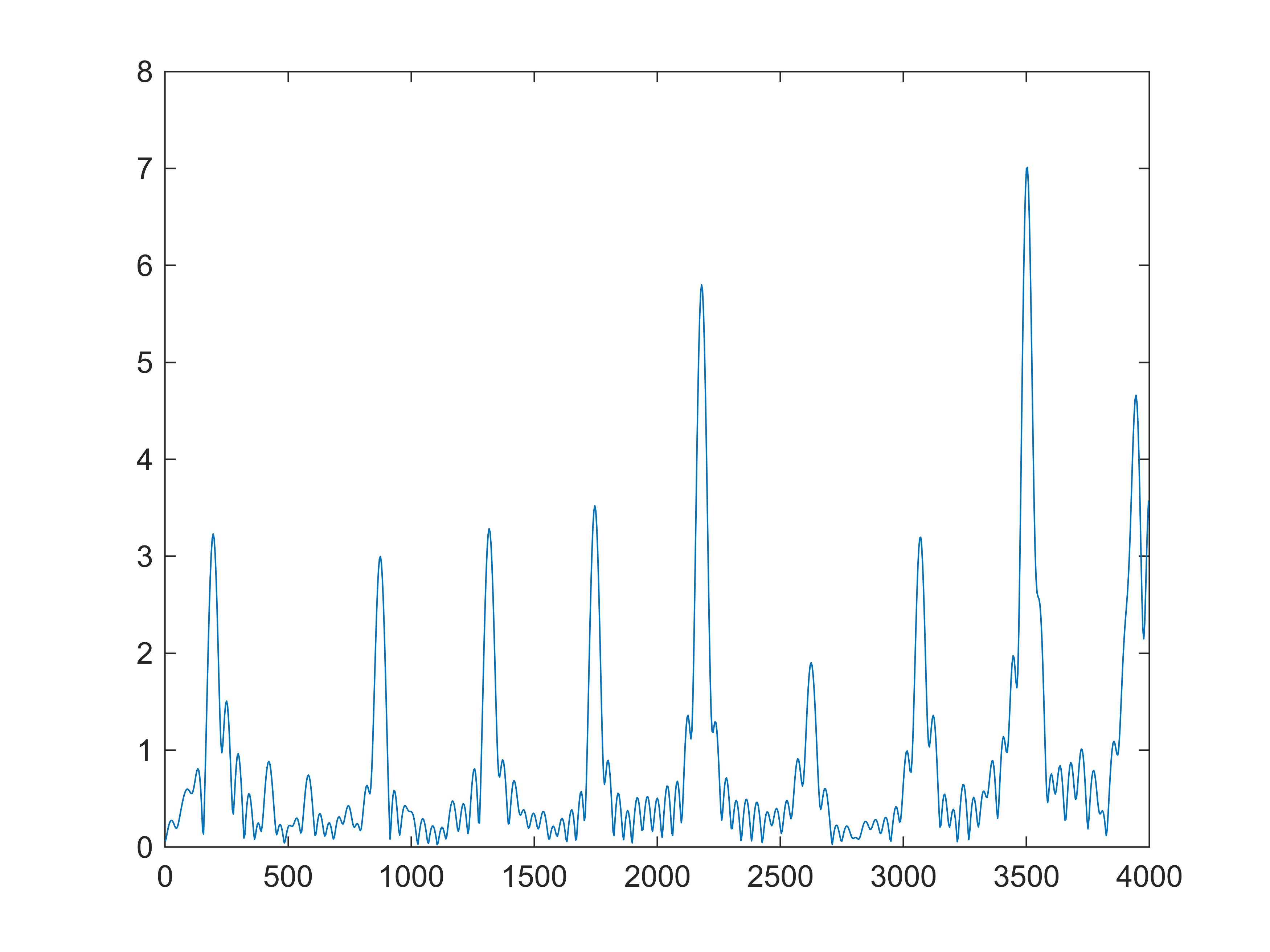
matlab
Yn1=D/fs*fft(yn1(8000:8099),N); % 2点取 1点后,200点长变成了 100点长
plot((0:N/2-1)*fs/(N*D),abs(Yn1(1:N/2)));% 模拟域幅度谱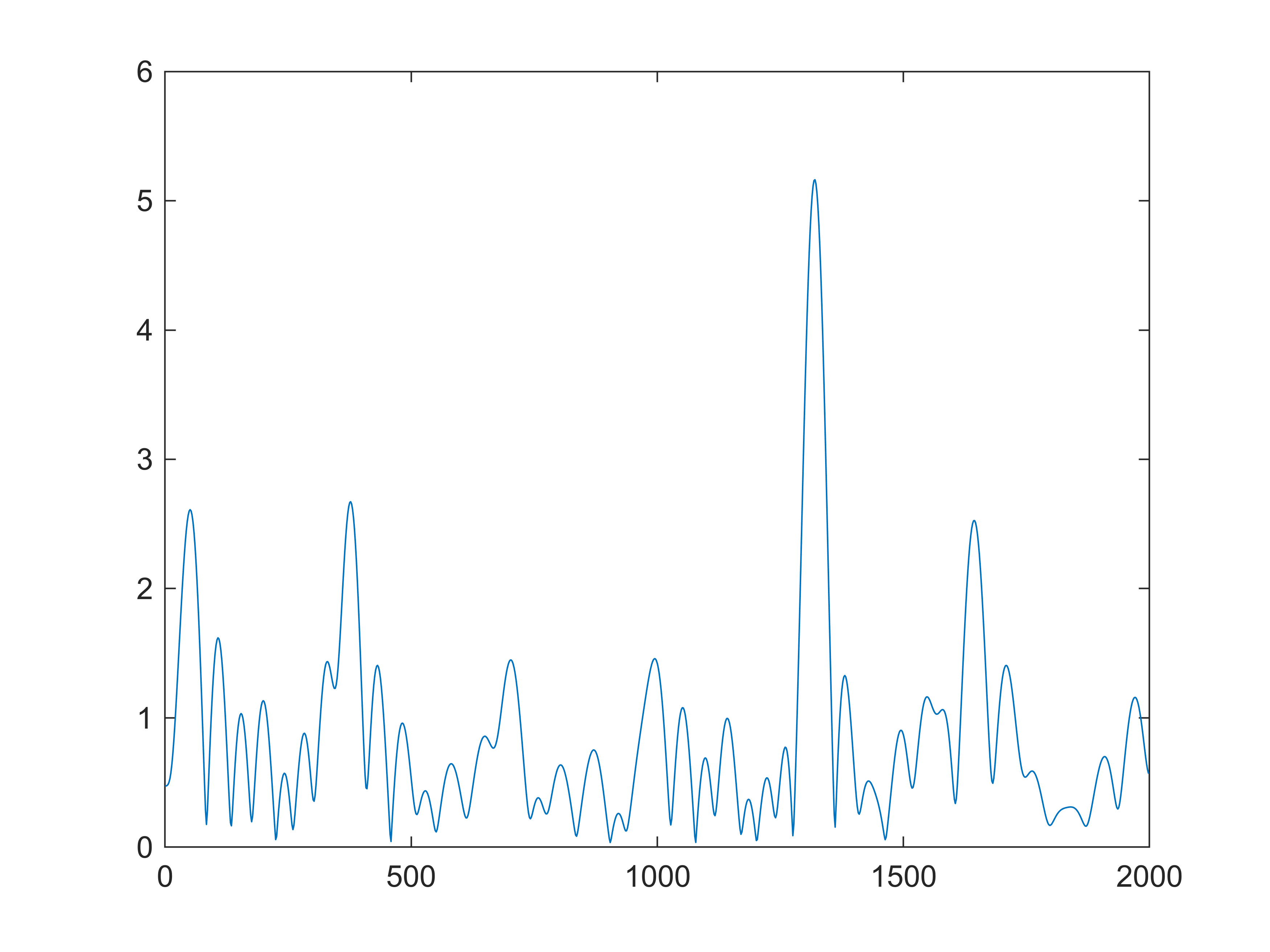
(3)对xn 先进行抗混叠滤波,再进行D=2 的整数倍抽取,得到音频信号yn2。
matlab
[xn,fs] = audioread( ".\2024-2025(1)《信号处理实验》资料(请拷贝到u盘中," + ...
"每次试验带到实验室)\实验中用到的一些函数和音频图像文件\motherland.wav");
D=2;N=2048;
% 低通滤波器参数
wp = 0.45*pi; % 通带截止频率
ws = 0.55*pi; % 阻带截止频率
Rp = 1; % 通带衰减 (dB)
As = 20; % 阻带衰减 (dB)
Fs = 2000; % 采样频率
% 计算滤波器阶数和截止频率
[n, Wn] = buttord(wp/pi, ws/pi, Rp, As);
[b, a] = butter(n, Wn, 'low');
% 频域分析
[H, w] = freqz(b, a, 1024);
dbH = 20*log10(abs(H));
figure;
% 幅度响应
subplot(3,1,1);
plot(w/pi, abs(H));
ylabel('|H|');
title('低通滤波器 幅度响应');
axis([0, 1, 0, 1.1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.45, 0.55, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]); % 0.707 for -3dB point
grid on;
% 相位响应
subplot(3,1,2);
plot(w/pi, angle(H)/pi);
ylabel('\phi (\times\pi)');
title('低通滤波器 相位响应');
axis([0, 1, -1, 1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.45, 0.55, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1, 0, 1]);
grid on;
% 幅度衰减(dB)
subplot(3,1,3);
plot(w/pi, dbH);
ylabel('dB');
xlabel('归一化频率 (\times\pi)');
title('低通滤波器 幅度衰减(dB)');
axis([0, 1, -40, 5]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.45, 0.55, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-40, -20, -1, 0]);
grid on;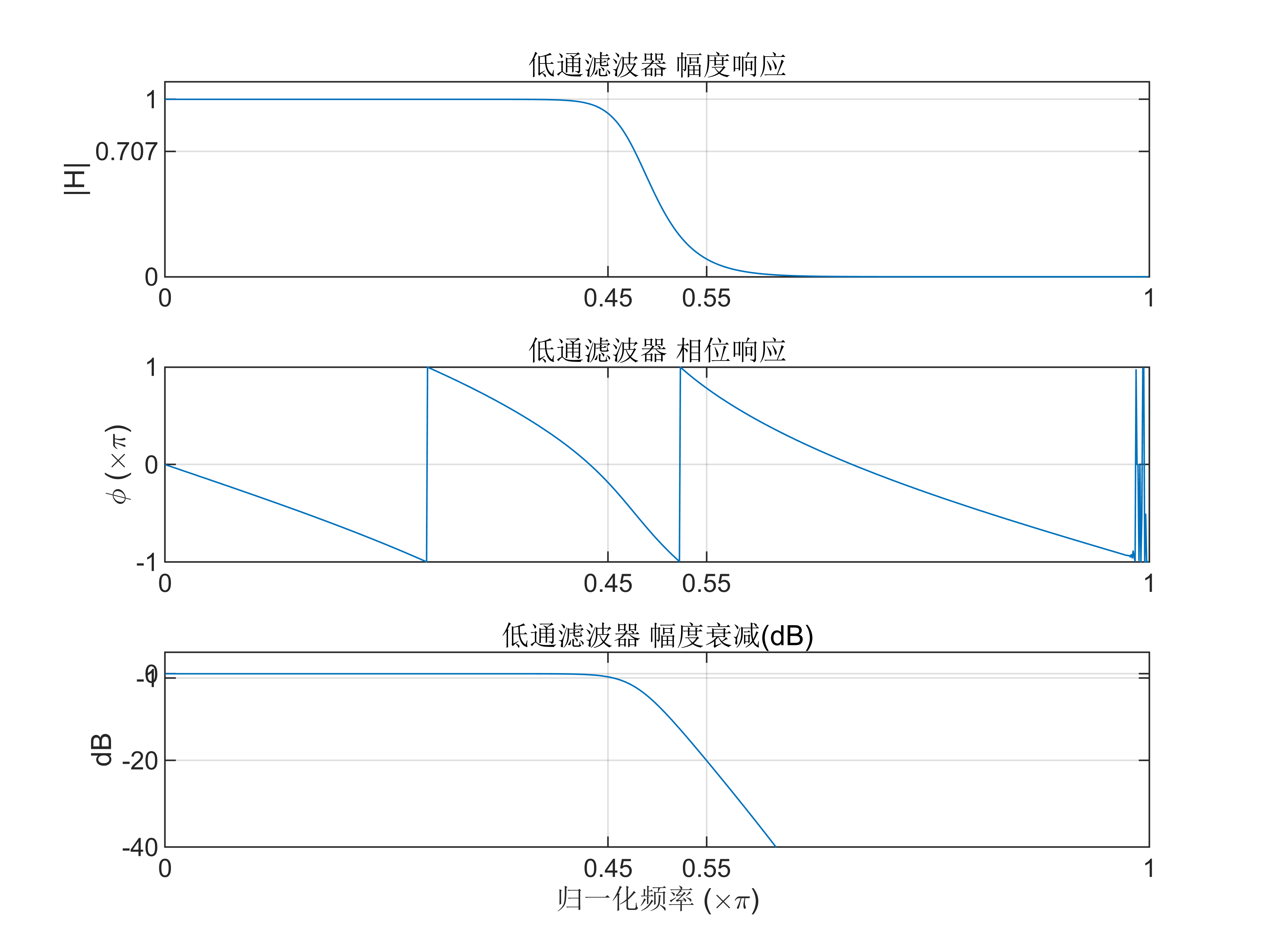
matlab
figure;
yn2=filter(b,a,xn); % 先滤波
yn2=yn2(1:D:length(xn)); % 再对滤波后的信号取点,每个 D-1个点抽取 1点 ,这里 D=2
Yn2=D/fs*fft(yn2(4000:4099),N);
plot((0:N/2-1)*fs/(D*N),abs(Yn2(1:N/2)));% 模拟域幅度谱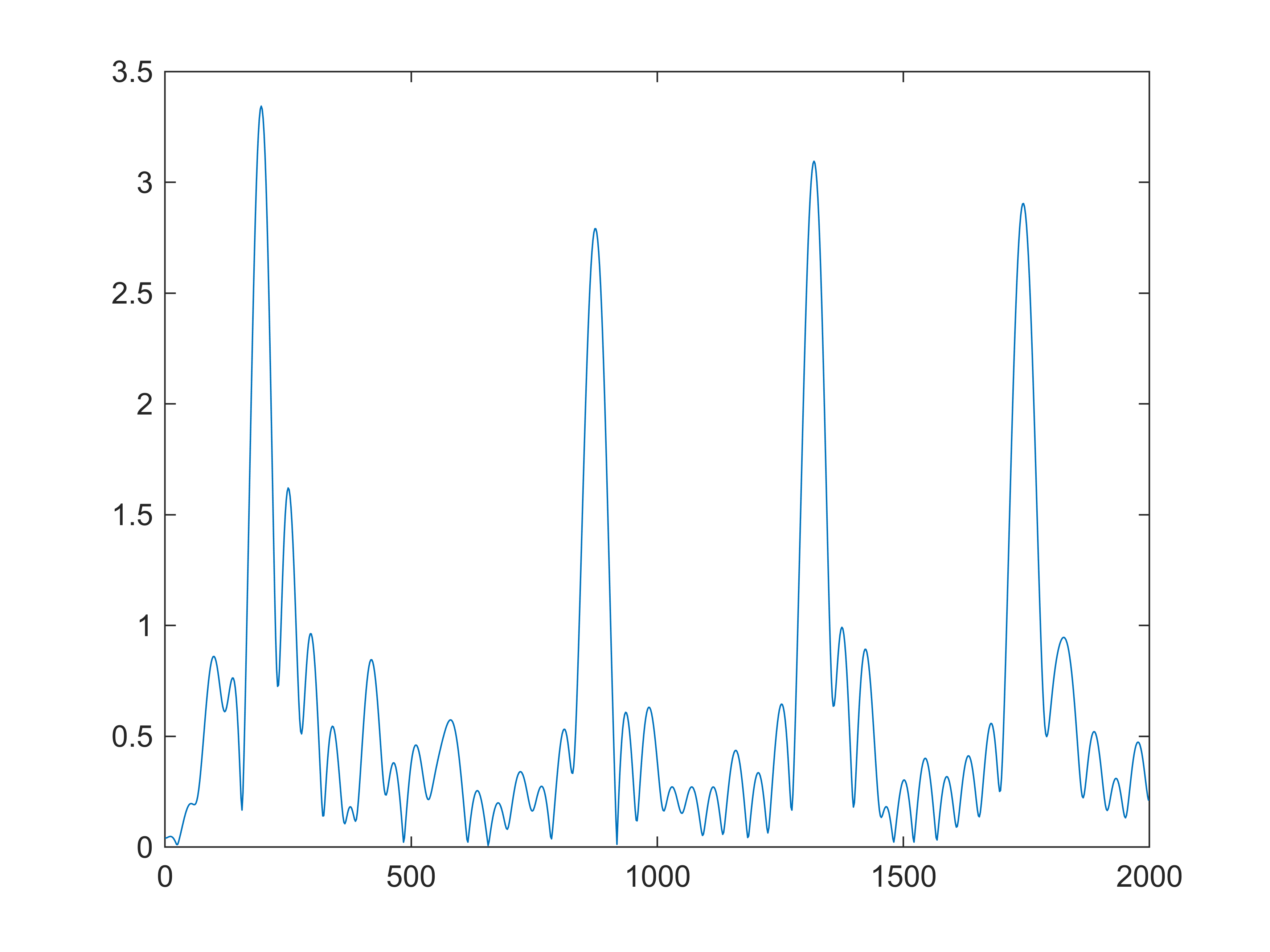
思考题
(1) 设计数字低通滤波器
要求 ωp=0.2π Rp=1dB阻带 ωs=0.35π As=15dB 滤波器采样频率 Fs=10Hz。
指标为:通带截止频率 ωp=0.2π,阻带截止频率ωs=0.3π,通带衰减 Rp=1dB,阻带衰减 As=20dB。
matlab
clear;
% 低通滤波器参数
wp = 0.2*pi; % 通带截止频率
ws = 0.3*pi; % 阻带截止频率
Rp = 1; % 通带衰减 (dB)
As = 20; % 阻带衰减 (dB)
Fs = 2000; % 采样频率
% 计算滤波器阶数和截止频率
[n, Wn] = buttord(wp/pi, ws/pi, Rp, As);
[b, a] = butter(n, Wn, 'low');
% 频域分析
[H, w] = freqz(b, a, 1024);
dbH = 20*log10(abs(H));
figure;
% 幅度响应
subplot(3,1,1);
plot(w/pi, abs(H));
ylabel('|H|');
title('低通滤波器 幅度响应');
axis([0, 1, 0, 1.1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.2, 0.3, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]); % 0.707 for -3dB point
grid on;
% 相位响应
subplot(3,1,2);
plot(w/pi, angle(H)/pi);
ylabel('\phi (\times\pi)');
title('低通滤波器 相位响应');
axis([0, 1, -1, 1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.2, 0.3, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1, 0, 1]);
grid on;
% 幅度衰减(dB)
subplot(3,1,3);
plot(w/pi, dbH);
ylabel('dB');
xlabel('归一化频率 (\times\pi)');
title('低通滤波器 幅度衰减(dB)');
axis([0, 1, -40, 5]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.2, 0.3, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-40, -20, -1, 0]);
grid on;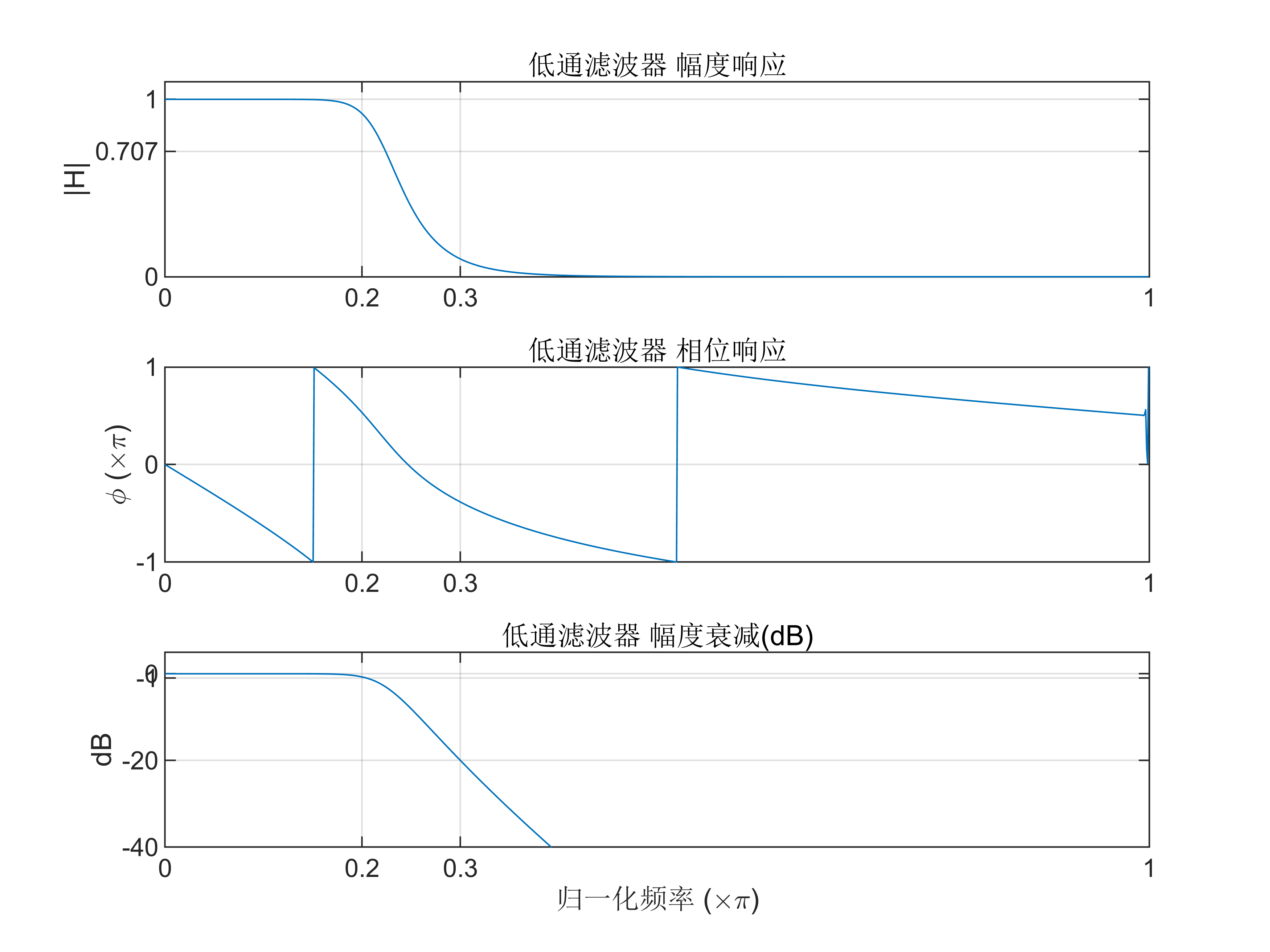
matlab
sys=tf(b,a,1/Fs)
matlabTextOutput
sys =
0.0001766 z^7 + 0.001236 z^6 + 0.003709 z^5 + 0.006182 z^4 + 0.006182 z^3 + 0.003709 z^2 + 0.001236 z + 0.0001766
-----------------------------------------------------------------------------------------------------------------
z^7 - 3.847 z^6 + 6.786 z^5 - 6.963 z^4 + 4.445 z^3 - 1.754 z^2 + 0.3944 z - 0.03885
采样时间: 0.0005 seconds
离散时间传递函数。
模型属性(2) 设计数字高通滤波器
指标为:阻带截止频率 ωs=0.4π,通带截 止频率ωp=0.6π,通带衰减 Rp=2dB,阻带衰减 As=30dB。
matlab
% 高通滤波器参数
ws = 0.4*pi; % 阻带截止频率
wp = 0.6*pi; % 通带截止频率
Rp = 2; % 通带衰减 (dB)
As = 30; % 阻带衰减 (dB)
Fs = 2000; % 采样频率
% 计算滤波器阶数和截止频率
[n, Wn] = buttord(wp/pi, ws/pi, Rp, As);
[b, a] = butter(n, Wn, 'high');
% 频域分析
[H, w] = freqz(b, a, 1024);
dbH = 20*log10(abs(H));
figure;
% 幅度响应
subplot(3,1,1);
plot(w/pi, abs(H));
ylabel('|H|');
title('高通滤波器 幅度响应');
axis([0, 1, 0, 1.1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.4, 0.6, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]); % 0.707 for -3dB point
grid on;
% 相位响应
subplot(3,1,2);
plot(w/pi, angle(H)/pi);
ylabel('\phi (\times\pi)');
title('高通滤波器 相位响应');
axis([0, 1, -1, 1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.4, 0.6, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1, 0, 1]);
grid on;
% 幅度衰减(dB)
subplot(3,1,3);
plot(w/pi, dbH);
ylabel('dB');
xlabel('归一化频率 (\times\pi)');
title('高通滤波器 幅度衰减(dB)');
axis([0, 1, -40, 5]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.4, 0.6, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-40, -20, -3, 0]);
grid on;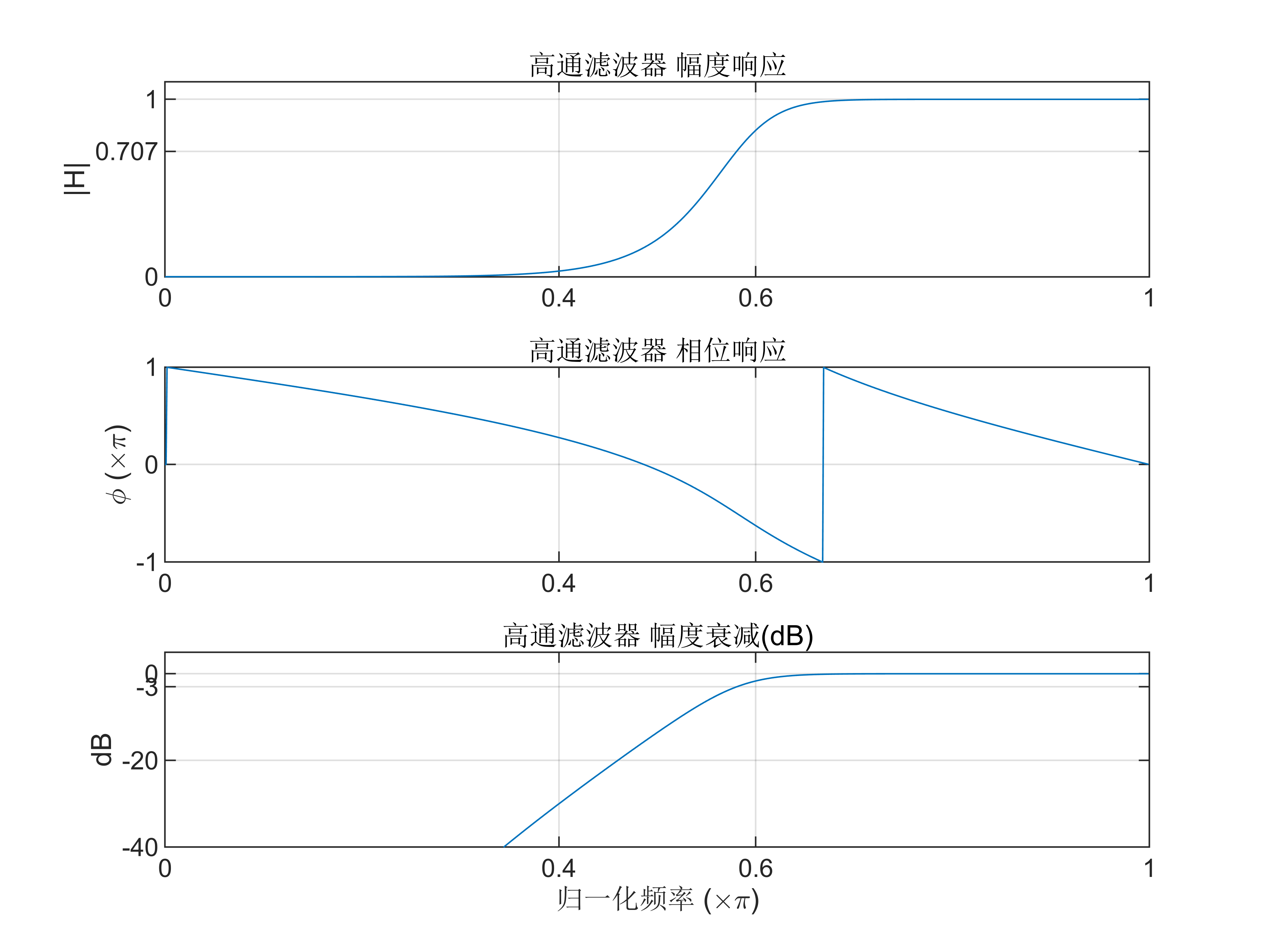
matlab
sys=tf(b,a,1/Fs)
matlabTextOutput
sys =
0.0129 z^6 - 0.07742 z^5 + 0.1935 z^4 - 0.2581 z^3 + 0.1935 z^2 - 0.07742 z + 0.0129
------------------------------------------------------------------------------------
z^6 + 0.9575 z^5 + 1.12 z^4 + 0.5115 z^3 + 0.2083 z^2 + 0.03757 z + 0.003764
采样时间: 0.0005 seconds
离散时间传递函数。
模型属性(3) 设计数字带通滤波器
指标为:通带范围 0.2π≤ωp≤0.6π,阻带范围 0≤ωs≤0.15π和 0.65π≤ωs≤π,通带衰减 Rp=1dB,阻带衰减 As=45dB。
matlab
% 带通滤波器参数
wp = [0.2 0.6]*pi; % 通带范围
ws = [0.15 0.65]*pi;% 阻带范围
Rp = 1; % 通带衰减 (dB)
As = 45; % 阻带衰减 (dB)
Fs = 2000; % 采样频率
% 计算滤波器阶数和截止频率
[n, Wn] = buttord(wp/pi, ws/pi, Rp, As);
[b, a] = butter(n, Wn, 'bandpass');
% 频域分析
[H, w] = freqz(b, a, 1024);
dbH = 20*log10(abs(H));
figure;
% 幅度响应
subplot(3,1,1);
plot(w/pi, abs(H));
ylabel('|H|');
title('带通滤波器 幅度响应');
axis([0, 1, 0, 1.1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.15, 0.2, 0.6, 0.65, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]);
grid on;
% 相位响应
subplot(3,1,2);
plot(w/pi, angle(H)/pi);
ylabel('\phi (\times\pi)');
title('带通滤波器 相位响应');
axis([0, 1, -1, 1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.15, 0.2, 0.6, 0.65, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1, 0, 1]);
grid on;
% 幅度衰减(dB)
subplot(3,1,3);
plot(w/pi, dbH);
ylabel('dB');
xlabel('归一化频率 (\times\pi)');
title('带通滤波器 幅度衰减(dB)');
axis([0, 1, -50, 5]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.15, 0.2, 0.6, 0.65, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-50, -20, -1, 0]);
grid on;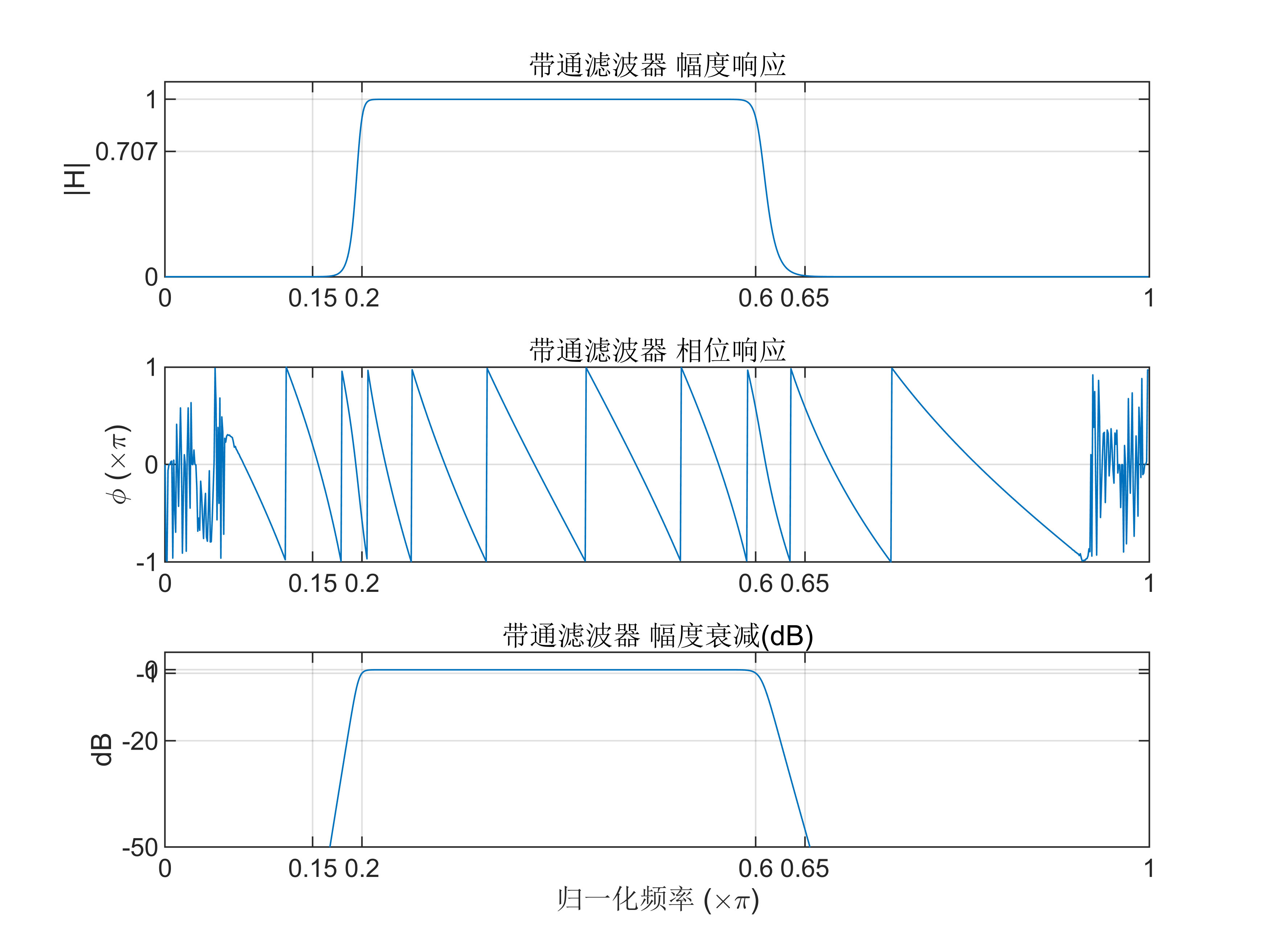
matlab
sys=tf(b,a,1/Fs)
matlabTextOutput
sys =
3.959e-08 z^46 - 9.105e-07 z^44 + 1.002e-05 z^42 - 7.011e-05 z^40 + 0.0003505 z^38 - 0.001332 z^36 + 0.003996 z^34 - 0.009705 z^32 + 0.01941 z^30 - 0.03235 z^28 + 0.04529 z^26 - 0.05352 z^24 + 0.05352 z^22 - 0.04529 z^20 + 0.03235 z^18 - 0.01941 z^16 + 0.009705 z^14 - 0.003996 z^12 + 0.001332 z^10 - 0.0003505 z^8 + 7.011e-05 z^6 - 1.002e-05 z^4 + 9.105e-07 z^2 - 3.959e-08
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
z^46 - 10.38 z^45 + 56.11 z^44 - 210.4 z^43 + 615.4 z^42 - 1497 z^41 + 3145 z^40 - 5854 z^39 + 9821 z^38 - 1.503e04 z^37 + 2.12e04 z^36 - 2.773e04 z^35 + 3.383e04 z^34 - 3.866e04 z^33 + 4.155e04 z^32 - 4.209e04 z^31 + 4.029e04 z^30 - 3.651e04 z^29 + 3.137e04 z^28 - 2.557e04 z^27 + 1.98e04 z^26 - 1.457e04 z^25 + 1.019e04 z^24 - 6772 z^23 + 4279 z^22 - 2568 z^21 + 1464 z^20 - 791.4 z^19 + 405.5 z^18 - 196.7 z^17 + 90.1 z^16 - 38.93 z^15 + 15.82 z^14 - 6.032 z^13 + 2.15 z^12 - 0.7134 z^11 + 0.2193 z^10 - 0.06209 z^9 + 0.01607 z^8 - 0.003763 z^7 + 0.0007882 z^6 - 0.0001452 z^5 + 2.301e-05 z^4 - 3.03e-06 z^3 + 3.138e-07 z^2 - 2.306e-08 z + 9.315e-10
采样时间: 0.0005 seconds
离散时间传递函数。
模型属性(4) 设计数字带阻滤波器
指标为:阻带范围 0.2π≤ωs≤0.6π,通带范围 0≤ωp≤0.15π和 0.65π≤ωp≤π,通带衰减 Rp=1dB,阻带衰减 As=45dB。
matlab
% 带阻滤波器参数
ws = [0.2 0.6]*pi; % 阻带范围
wp = [0.15 0.65]*pi;% 通带范围
Rp = 1; % 通带衰减 (dB)
As = 45; % 阻带衰减 (dB)
Fs = 2000; % 采样频率
% 计算滤波器阶数和截止频率
[n, Wn] = buttord(wp/pi, ws/pi, Rp, As);
[b, a] = butter(n, Wn, 'stop');
% 频域分析
[H, w] = freqz(b, a, 1024);
dbH = 20*log10(abs(H));
figure;
% 幅度响应
subplot(3,1,1);
plot(w/pi, abs(H));
ylabel('|H|');
title('带阻滤波器 幅度响应');
axis([0, 1, 0, 1.1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.15, 0.2, 0.6, 0.65, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [0, 0.707, 1]);
grid on;
% 相位响应
subplot(3,1,2);
plot(w/pi, angle(H)/pi);
ylabel('\phi (\times\pi)');
title('带阻滤波器 相位响应');
axis([0, 1, -1, 1]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.15, 0.2, 0.6, 0.65, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-1, 0, 1]);
grid on;
% 幅度衰减(dB)
subplot(3,1,3);
plot(w/pi, dbH);
ylabel('dB');
xlabel('归一化频率 (\times\pi)');
title('带阻滤波器 幅度衰减(dB)');
axis([0, 1, -50, 5]);
set(gca, 'XTickMode', 'manual', 'XTick', [0, 0.15, 0.2, 0.6, 0.65, 1]);
set(gca, 'YTickMode', 'manual', 'YTick', [-50, -20, -1, 0]);
grid on;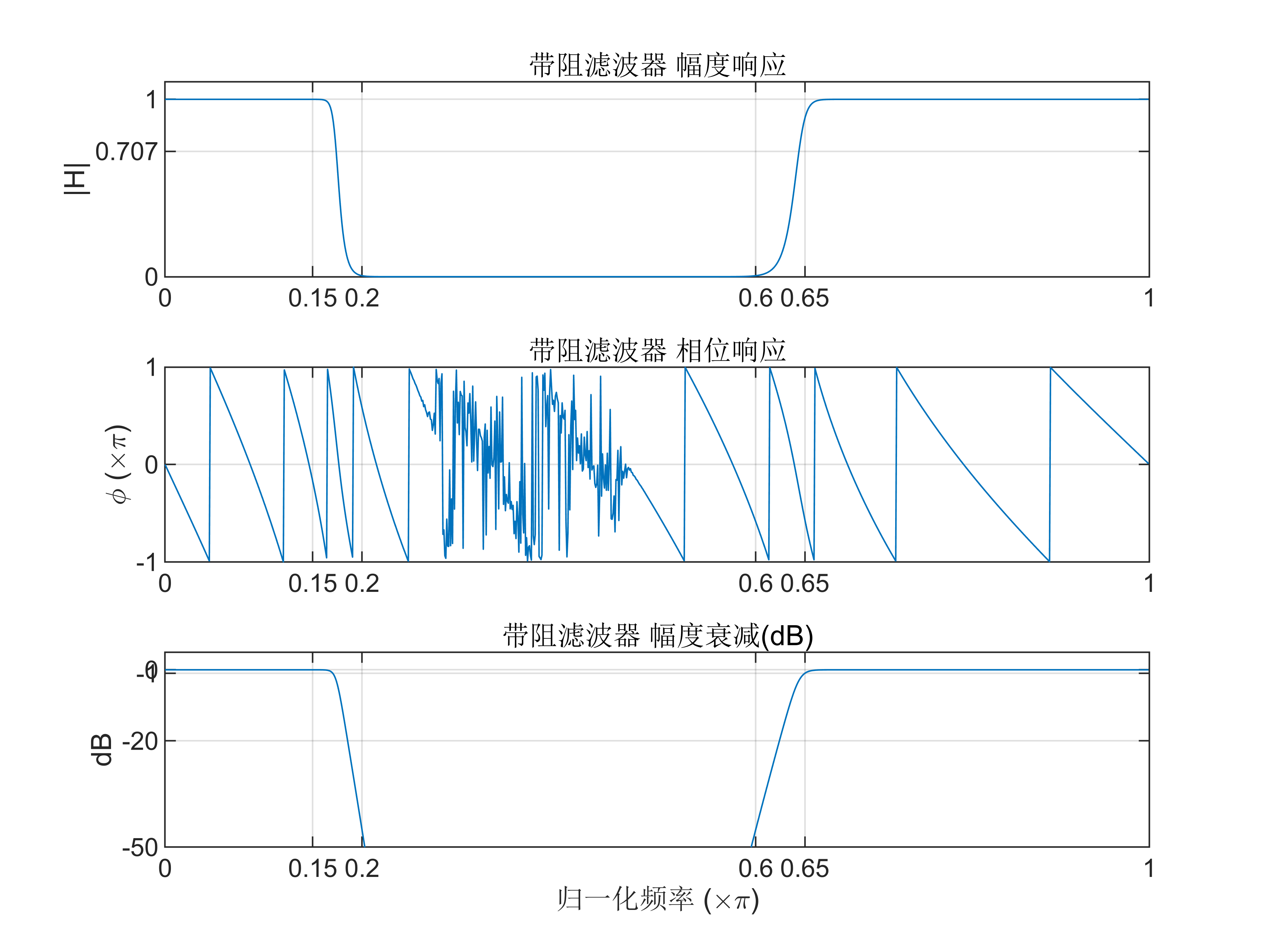
matlab
sys=tf(b,a,1/Fs)
matlabTextOutput
sys =
4.255e-06 z^46 - 7.477e-05 z^45 + 0.0007263 z^44 - 0.005006 z^43 + 0.02711 z^42 - 0.1218 z^41 + 0.4689 z^40 - 1.583 z^39 + 4.764 z^38 - 12.93 z^37 + 31.93 z^36 - 72.32 z^35 + 151 z^34 - 292.3 z^33 + 526.4 z^32 - 884.5 z^31 + 1391 z^30 - 2050 z^29 + 2840 z^28 - 3700 z^27 + 4541 z^26 - 5253 z^25 + 5732 z^24 - 5901 z^23 + 5732 z^22 - 5253 z^21 + 4541 z^20 - 3700 z^19 + 2840 z^18 - 2050 z^17 + 1391 z^16 - 884.5 z^15 + 526.4 z^14 - 292.3 z^13 + 151 z^12 - 72.32 z^11 + 31.93 z^10 - 12.93 z^9 + 4.764 z^8 - 1.583 z^7 + 0.4689 z^6 - 0.1218 z^5 + 0.02711 z^4 - 0.005006 z^3 + 0.0007263 z^2 - 7.477e-05 z + 4.255e-06
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
z^46 - 9.312 z^45 + 43.3 z^44 - 136 z^43 + 330.4 z^42 - 671 z^41 + 1192 z^40 - 1900 z^39 + 2755 z^38 - 3677 z^37 + 4557 z^36 - 5277 z^35 + 5736 z^34 - 5875 z^33 + 5687 z^32 - 5216 z^31 + 4540 z^30 - 3756 z^29 + 2957 z^28 - 2217 z^27 + 1583 z^26 - 1078 z^25 + 699.6 z^24 - 432.8 z^23 + 255 z^22 - 143.1 z^21 + 76.44 z^20 - 38.81 z^19 + 18.71 z^18 - 8.552 z^17 + 3.7 z^16 - 1.512 z^15 + 0.5821 z^14 - 0.2106 z^13 + 0.07131 z^12 - 0.02251 z^11 + 0.006592 z^10 - 0.00178 z^9 + 0.0004398 z^8 - 9.845e-05 z^7 + 1.973e-05 z^6 - 3.483e-06 z^5 + 5.288e-07 z^4 - 6.667e-08 z^3 + 6.633e-09 z^2 - 4.7e-10 z + 1.787e-11
采样时间: 0.0005 seconds
离散时间传递函数。
模型属性