KAN解possion 方程，方程构造篇代码阅读

爱喝热水的呀哈喽2024-11-28 10:38
python 复制代码 
from kan import *
import matplotlib.pyplot as plt
from torch import autograd
from tqdm import tqdm

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)

dim = 2
np_i = 21 # number of interior points (along each dimension)
np_b = 21 # number of boundary points (along each dimension)
ranges = [-1, 1]

model = KAN(width=[2,2,1], grid=5, k=3, seed=1, device=device)

def batch_jacobian(func, x, create_graph=False):
    # x in shape (Batch, Length)
    def _func_sum(x):
        return func(x).sum(dim=0)
    return autograd.functional.jacobian(_func_sum, x, create_graph=create_graph).permute(1,0,2)

# define solution
sol_fun = lambda x: torch.sin(torch.pi*x[:,[0]])*torch.sin(torch.pi*x[:,[1]])
source_fun = lambda x: -2*torch.pi**2 * torch.sin(torch.pi*x[:,[0]])*torch.sin(torch.pi*x[:,[1]])

# interior
sampling_mode = 'random' # 'radnom' or 'mesh'

x_mesh = torch.linspace(ranges[0],ranges[1],steps=np_i)
y_mesh = torch.linspace(ranges[0],ranges[1],steps=np_i)
X, Y = torch.meshgrid(x_mesh, y_mesh, indexing="ij")
if sampling_mode == 'mesh':
    #mesh
    x_i = torch.stack([X.reshape(-1,), Y.reshape(-1,)]).permute(1,0)
else:
    #random
    x_i = torch.rand((np_i**2,2))*2-1
    
x_i = x_i.to(device)

# boundary, 4 sides
helper = lambda X, Y: torch.stack([X.reshape(-1,), Y.reshape(-1,)]).permute(1,0)
xb1 = helper(X[0], Y[0])
xb2 = helper(X[-1], Y[0])
xb3 = helper(X[:,0], Y[:,0])
xb4 = helper(X[:,0], Y[:,-1])
x_b = torch.cat([xb1, xb2, xb3, xb4], dim=0)

x_b = x_b.to(device)

steps = 20
alpha = 0.01
log = 1

def train():
    optimizer = LBFGS(model.parameters(), lr=1, history_size=10, line_search_fn="strong_wolfe", tolerance_grad=1e-32, tolerance_change=1e-32, tolerance_ys=1e-32)

    pbar = tqdm(range(steps), desc='description', ncols=100)

    for _ in pbar:
        def closure():
            global pde_loss, bc_loss
            optimizer.zero_grad()
            # interior loss
            sol = sol_fun(x_i)
            sol_D1_fun = lambda x: batch_jacobian(model, x, create_graph=True)[:,0,:]
            sol_D1 = sol_D1_fun(x_i)
            sol_D2 = batch_jacobian(sol_D1_fun, x_i, create_graph=True)[:,:,:]
            lap = torch.sum(torch.diagonal(sol_D2, dim1=1, dim2=2), dim=1, keepdim=True)
            source = source_fun(x_i)
            pde_loss = torch.mean((lap - source)**2)

            # boundary loss
            bc_true = sol_fun(x_b)
            bc_pred = model(x_b)
            bc_loss = torch.mean((bc_pred-bc_true)**2)

            loss = alpha * pde_loss + bc_loss
            loss.backward()
            return loss

        if _ % 5 == 0 and _ < 50:
            model.update_grid_from_samples(x_i)

        optimizer.step(closure)
        sol = sol_fun(x_i)
        loss = alpha * pde_loss + bc_loss
        l2 = torch.mean((model(x_i) - sol)**2)

        if _ % log == 0:
            pbar.set_description("pde loss: %.2e | bc loss: %.2e | l2: %.2e " % (pde_loss.cpu().detach().numpy(), bc_loss.cpu().detach().numpy(), l2.cpu().detach().numpy()))

train()

这里jacobi计算的sum dim=0如何理解

batch_jacobian 函数用于计算给定函数 func 关于输入 x 的雅可比矩阵。这里的 x 是一个形状为 (Batch, Length) 的张量，其中 Batch 表示批次大小，Length 表示每个批次中向量的长度。

函数 _func_sum 是在 batch_jacobian 中定义的，它的目的是将 func 应用于输入 x 后的结果在维度 0 上求和。这里的维度 0 是批次维度。具体来说，func(x) 的输出形状是 (Batch, OutputLength)，其中 OutputLength 是函数 func 输出的长度。对 func(x) 在维度 0 上求和，即对每个批次的结果进行累加，得到一个形状为 (OutputLength,) 的张量。

下面是对 sum(dim=0) 的详细解释：

  • func(x).sum(dim=0): 这个操作是对 func(x) 的输出在批次维度（即第0维）上进行求和。这意味着，如果 func 输出的每个批次的结果是独立的，通过对批次维度求和，实际上是将所有批次的结果合并成了一个单一的向量。

为什么要这样做呢？这是因为在计算雅可比矩阵时，我们关心的是函数输出关于输入的偏导数。如果函数的输出是批次的，直接计算雅可比矩阵将会得到每个批次输出的偏导数。通过对批次维度求和，我们实际上是在计算所有批次输出的平均效应的偏导数，这在很多情况下是需要的，特别是当我们希望雅可比矩阵反映的是整个批次数据的平均梯度时。

在物理或偏微分方程（PDE）的上下文中，这通常意味着我们关注的是整个域上的平均行为，而不是单个样本的行为。因此，通过对批次维度求和，_func_sum 函数将多个样本的输出汇总为一个单一的输出，从而使得 jacobian 函数计算的是这个汇总输出关于输入的梯度。

在您的代码中，这样的处理可能是为了确保 PDE 的残差（即 lap - source）是在整个内部点集上的平均损失，而不是单个点上的损失。这有助于算法更好地捕捉整个解空间的性质。

lap = torch.sum(torch.diagonal(sol_D2, dim1=1, dim2=2), dim=1, keepdim=True)如何理解

lap 是用来计算拉普拉斯算子（Laplacian）的值的。拉普拉斯算子是一个二阶微分算子，它测量一个函数在其定义域上的局部曲率。在多维空间中，拉普拉斯算子可以通过计算函数梯度（即一阶导数）的散度（即二阶导数）来得到。

让我们分解 lap = torch.sum(torch.diagonal(sol_D2, dim1=1, dim2=2), dim=1, keepdim=True) 这行代码：

  1. sol_D2: 这是一个形状为 (Batch, Length, Length) 的张量，它代表了对 sol_D1_fun 的输入 x_i 进行批处理雅可比计算的结果。sol_D2 实际上是一个 Hessian 矩阵，即关于输入 x_i 的二阶导数。

  2. torch.diagonal(sol_D2, dim1=1, dim2=2): 这个操作提取了 sol_D2 张量的对角线元素。参数 dim1=1 和 dim2=2 指定了要提取对角线的维度。具体来说，对于每个批次（即 Batch 维度），它会从形状为 (Length, Length) 的 Hessian 矩阵中提取对角线元素，形成一个形状为 (Batch, Length) 的张量。

  3. torch.sum(...): 这个操作对提取出的对角线元素进行求和。由于对角线元素张量的形状是 (Batch, Length)，sum 函数在维度 dim=1 上进行操作，即对每个批次中的对角线元素进行求和。结果是一个形状为 (Batch, 1) 的张量，因为 keepdim=True 保持了求和操作的维度。

  4. keepdim=True: 这个参数确保了在求和操作后，结果的形状仍然是 (Batch, 1) 而不是 (Batch,)。这有助于在后续的计算中保持张量的维度一致。

综上所述，lap 是每个批次中 Hessian 矩阵对角线元素的和，它代表了对每个输入向量 x_i 的函数 sol_D1_fun 的二阶导数沿对角线求和的结果。在物理和偏微分方程的上下文中，这通常对应于计算函数的二阶导数之和，即拉普拉斯算子的作用。因此，lap 可以被视为一个批次的拉普拉斯算子值。

def batch_jacobian(func, x, create_graph=False): # x in shape (Batch, Length) def _func_sum(x): return func(x).sum(dim=0) return autograd.functional.jacobian(_func_sum, x, create_graph=create_graph).permute(1,0,2) sol = sol_fun(x_i) sol_D1_fun = lambda x: batch_jacobian(model, x, create_graph=True)[:,0,:] sol_D1 = sol_D1_fun(x_i) sol_D2 = batch_jacobian(sol_D1_fun, x_i, create_graph=True)[:,:,:] lap = torch.sum(torch.diagonal(sol_D2, dim1=1, dim2=2), dim=1, keepdim=True) 具体

解释jacobi计算过程

逐行解释

def batch_jacobian(func, x, create_graph=False):
    # x in shape (Batch, Length)
    def _func_sum(x):
        return func(x).sum(dim=0)
    return autograd.functional.jacobian(_func_sum, x, create_graph=create_graph).permute(1,0,2)
  • 定义了一个函数 batch_jacobian，它接受一个函数 func、一个输入张量 x 和一个布尔值 create_graph。
  • x 是一个形状为 (Batch, Length) 的张量，其中 Batch 是批次大小，Length 是每个批次中向量的长度。
  • 在 batch_jacobian 函数内部，定义了一个内部函数 _func_sum，它对 func(x) 的输出在维度 0 上求和**，即将批次中的所有输出相加，得到一个形状为 (OutputLength,) 的张量。**
  • 使用 autograd.functional.jacobian 计算 _func_sum 关于 x 的雅可比矩阵。create_graph 参数控制是否在计算梯度时创建计算图，这对于后续的梯度计算是有用的。
  • 返回的雅可比矩阵经过 permute(1,0,2) 操作，改变了其维度顺序，使其形状变为 (Batch, Length, OutputLength)。

接下来是代码的实际应用部分：

python

复制

sol = sol_fun(x_i)
  • sol_fun 是一个函数，它接受输入 x_i（形状为 (Batch, Length)）并返回一个形状为 (Batch, OutputLength) 的张量，这通常表示在内部点 x_i 上 PDE 解的值。
  • sol 是 sol_fun 在 x_i 上的输出。

python

复制

sol_D1_fun = lambda x: batch_jacobian(model, x, create_graph=True)[:,0,:]
  • 定义了一个匿名函数 sol_D1_fun，它使用前面定义的 batch_jacobian 函数来计算模型 model 关于输入 x 的雅可比矩阵。
  • [:,0,:] 是一个切片操作，它选择每个批次中雅可比矩阵的第一个元素（即第一个输出分量关于输入的偏导数），得到一个形状为 (Batch, Length) 的张量。

python

复制

sol_D1 = sol_D1_fun(x_i)
  • sol_D1 是将 sol_D1_fun 应用于内部点 x_i 的结果，它表示在 x_i 上模型 model 关于输入的第一个偏导数。

python

复制

sol_D2 = batch_jacobian(sol_D1_fun, x_i, create_graph=True)[:,:,:]
  • 使用 batch_jacobian 函数计算 sol_D1_fun 关于 x_i 的雅可比矩阵，这实际上是计算二阶导数。
  • [:,:,:] 是一个切片操作，它返回整个雅可比矩阵，不进行任何裁剪。

python

复制

lap = torch.sum(torch.diagonal(sol_D2, dim1=1, dim2=2), dim=1, keepdim=True)
  • 使用 torch.diagonal 提取 sol_D2 的对角线元素，这些元素代表了对每个批次中输入向量的二阶导数。
  • torch.sum 对这些对角线元素进行求和，计算每个批次中所有二阶导数的和。
  • dim=1 指定了求和的维度，即对每个批次进行操作。
  • keepdim=True 确保结果张量的形状为 (Batch, 1) 而不是 (Batch,)，这样可以在后续计算中保持维度的一致性。
  • lap 是一个形状为 (Batch, 1) 的张量，代表每个批次中输入向量的拉普拉斯算子值。

、

它对 `func(x)` 的输出在维度 0 上求和，即将批次中的所有输出相加，得到一个形状为 `(OutputLength,)` 的张量。

解释

首先，让我们明确 func(x) 的输出形状。假设 func 是一个函数，它接受一个形状为 (Batch, Length) 的输入张量 x，并输出一个形状为 (Batch, OutputLength) 的张量。这里的 Batch 表示批次大小，Length 表示输入向量的长度，而 OutputLength 表示函数输出的长度。

当我们调用 func(x) 时，对于每个批次中的输入向量 x，我们都会得到一个对应的输出向量。因此，如果我们有 Batch 个输入向量，我们就会有 Batch 个输出向量，每个输出向量的长度为 OutputLength。

现在，让我们关注到 _func_sum(x) 的定义：

python

复制

def _func_sum(x):
    return func(x).sum(dim=0)

在这个定义中，.sum(dim=0) 是关键部分。dim=0 指定了求和的维度，即批次维度。这意味着，对于 func(x) 输出的形状为 (Batch, OutputLength) 的张量，我们将沿着批次维度（即第一个维度）进行求和。

具体来说，这个过程是这样的：

  1. func(x) 输出的形状是 (Batch, OutputLength)。我们可以将其视为一个矩阵，其中每一行对应一个批次中的输出向量。

  2. 当我们调用 .sum(dim=0) 时，我们实际上是在对这个矩阵的每一列进行求和。也就是说，对于每个 OutputLength 的索引位置 j，我们将所有批次中的第 j 个元素相加。

  3. 求和的结果是一个形状为 (OutputLength,) 的一维张量。这是因为我们已经将所有批次中的对应输出元素相加了，不再有批次维度。

例如，如果 Batch=3 且 OutputLength=2，那么 func(x) 的输出可能看起来像这样：

复制

[
  [a1, b1],  # 第一个批次的输出
  [a2, b2],  # 第二个批次的输出
  [a3, b3]   # 第三个批次的输出
]

当我们对 dim=0 进行求和时，结果将是：

复制

[a1+a2+a3, b1+b2+b3]

这个结果是一个形状为 (OutputLength,) 的张量，即 [sum_of_a, sum_of_b]。

总之，通过在维度 0 上求和，我们得到了一个反映所有批次输出总和的一维张量，而不是每个批次单独的输出。这在计算雅可比矩阵时很有用，因为它允许我们考虑整个批次的数据，而不是单个样本。

def batch_jacobian(func, x, create_graph=False): # x in shape (Batch, Length) def _func_sum(x): return func(x).sum(dim=0) return autograd.functional.jacobian(_func_sum, x, create_graph=create_graph).permute(1,0,2) 再

详细解释jacobi

def batch_jacobian(func, x, create_graph=False):
    # x in shape (Batch, Length)
    def _func_sum(x):
        return func(x).sum(dim=0)
    return autograd.functional.jacobian(_func_sum, x, create_graph=create_graph).permute(1,0,2)

这个函数的目的是计算一个函数 func 关于输入 x 的雅可比矩阵。雅可比矩阵是一个矩阵，其中包含了函数在给定点处对每个输入变量的偏导数。

  1. 函数定义和输入参数:

    • func: 一个接受形状为 (Batch, Length) 的张量 x 作为输入的函数。
    • x: 输入张量，形状为 (Batch, Length)，其中 Batch 是批次大小，Length 是每个批次中向量的长度。
    • create_graph: 一个布尔值，指定是否在计算梯度时创建计算图。如果设置为 True，则可以在后续的计算中使用梯度。

  2. 内部函数 _func_sum:

    • _func_sum 是一个内部定义的辅助函数，它接受与 func 相同的输入 x。
    • 在 _func_sum 中，func(x) 被调用以计算 func 在输入 x 上的输出。
    • .sum(dim=0) 是对 func(x) 的输出在批次维度（即第一个维度）上进行求和。由于 func(x) 的输出形状是 (Batch, OutputLength)，求和操作将每个批次中的相同位置元素相加，结果是一个形状为 (OutputLength,) 的一维张量。

  3. 计算雅可比矩阵:

    • autograd.functional.jacobian 用于计算 _func_sum 关于输入 x 的雅可比矩阵。
    • 由于 _func_sum 是对 func(x) 输出的批次维度求和，雅可比矩阵将反映 func 在所有批次上的平均偏导数。
    • create_graph=create_graph 参数传递给 jacobian 函数，以确定是否需要创建计算图。

  4. 雅可比矩阵的维度重排:

    • permute(1,0,2) 是对计算出的雅可比矩阵进行维度重排。由于 jacobian 函数的输出形状是 (OutputLength, Batch, Length)，重排后的形状变为 (Batch, OutputLength，Length,)。

    • permute(1,0,2) 是一个在深度学习框架（如PyTorch）中常用的操作，用于改变一个多维数组（张量）的维度顺序。

      这个操作的含义是将输入张量的维度按照给定的索引顺序进行重排。具体来说，permute 函数的参数是一个索引列表，列表中的每个数字代表原始张量中的一个维度，数字的顺序决定了重排后维度的顺序。

    • 这种维度重排使得雅可比矩阵的形状与输入张量 x 的形状对齐，其中 Batch 和 Length 维度分别对应于输入张量的批次和长度，而 OutputLength 维度对应于函数输出的长度。

综上所述，batch_jacobian 函数计算了一个函数 func 关于输入 x 的雅可比矩阵，并返回了一个形状为 (Batch, Length, OutputLength) 的张量，其中包含了函数 func 在每个输入位置处的偏导数。

关于np带方向求和

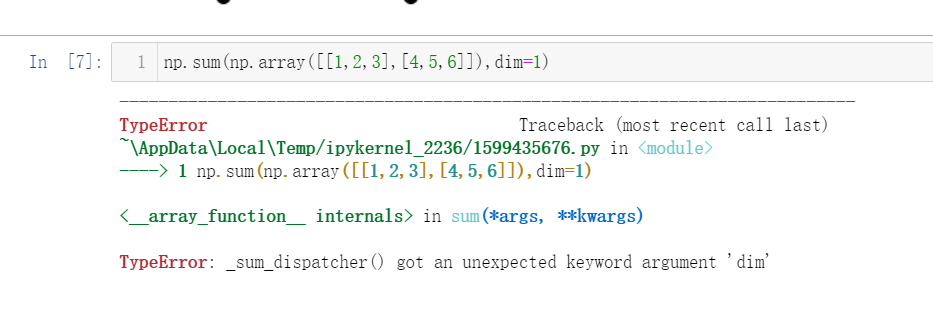
需要删除代码中的dim=1参数，因为numpy.sum()函数不支持这个参数。这里是更正后的代码：

python

复制

np.sum(np.array([[1,2,3],[4,5,6]]))

这段代码会计算二维数组中所有元素的和。如果你想沿着某个轴求和，可以使用axis参数，例如：

python

复制

np.sum(np.array([[1,2,3],[4,5,6]]), axis=0)

这将会计算每列的和。如果你想要计算每行的和，可以将axis设置为1：

python

复制

np.sum(np.array([[1,2,3],[4,5,6]]), axis=1)

tensor 1.0000

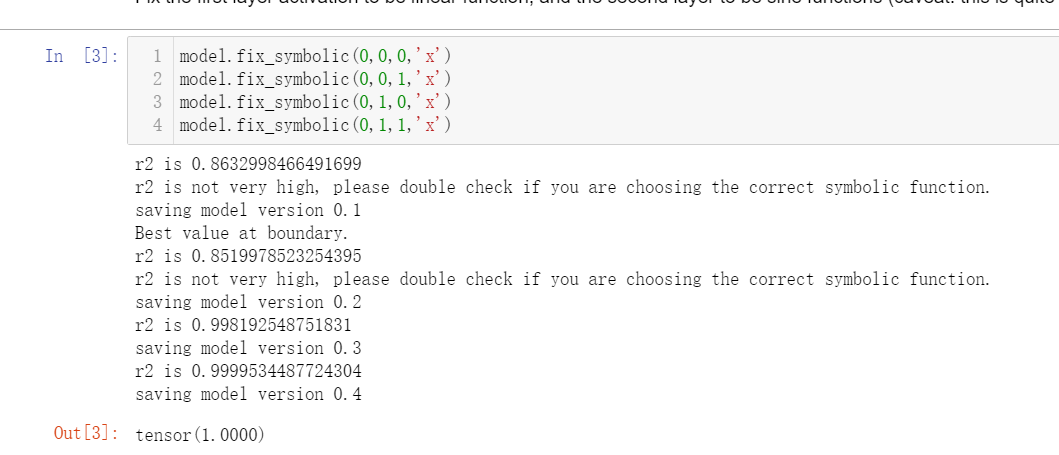
引用

在Python编程语言中，特别是当涉及到机器学习库如TensorFlow或PyTorch时，tensor(1.0000) 表示一个标量张量（scalar tensor），其值为1.0。这里的数字1后面跟着四个零和小数点，表示它是一个浮点数，精确到小数点后四位。

具体来说：

  • tensor 是指这个数值是以张量的形式存在的，尽管在这个例子中它只是一个单一的值（即标量）。
  • (1.0000) 表示该标量张量的值是1.0。

在深度学习和科学计算中，使用张量来存储和处理数据是很常见的，即使对于单个数值也是如此。这样做可以保持代码的一致性，使得处理更复杂的数据结构时更加方便。

相关推荐
今天补充能量了吗13 分钟前
T3 TensorFlow入门实战——天气识别
人工智能·python·tensorflow
不知不道abc24 分钟前
使用Azure合成语音，解放嘴巴（bushi）
python·音频
知识中的海王27 分钟前
已解决ModuleNotFoundError: No module named ‘selenium‘
python·selenium
叫我：松哥30 分钟前
经典游戏：飞机大战游戏python设计与实现
开发语言·python·游戏·pygame
埃菲尔铁塔_CV算法1 小时前
条件数：概念、矩阵中的应用及实际工业场景应用
人工智能·python·线性代数·算法·matlab·矩阵
Misnearch1 小时前
sklearn.ensemble
人工智能·python·sklearn
芷芷在学习1 小时前
机器学习（二十五）：决策树算法以及决策树和神经网络的对比
人工智能·机器学习
2402_871321951 小时前
Matlab与python数据处理对比
python·gpt·学习·算法·matlab
Adunn1 小时前
算法基础 - 最小二乘法（线性拟合）
c++·人工智能·算法·机器学习·自动驾驶·最小二乘法
DevinLGT1 小时前
石英晶体基本特性和等效电路：【图文讲解】
人工智能·单片机·嵌入式硬件
热门推荐
01软件工程从理论到实践客观题汇总(头歌第一章至第八章)02(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明03【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总04基于微信小程序的自习室预约系统的设计与实现05玄机平台应急响应—webshell查杀06PyTorch机器学习实现液态神经网络07Docker 夺命连环 15 问0804 - matlab m_map地学绘图工具基础函数 - 设置网格09RAG 实践- Ollama+RagFlow 部署本地知识库10【软考经验分享】软考-中级-嵌入式备考