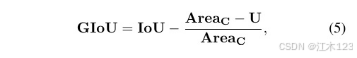摘要 :在2D/3D目标检测任务中,IoU (Intersection-over- Union)作为一种评价指标,被广泛用于评价不同探测器在测试阶段的性能。然而,在训练阶段,通常采用常见的距离损失(如L1或L2)作为损失函数,以最小化预测值与真实值边界盒(Bbox)之间的差异。为了消除训练和测试之间的性能差距,在[1]和[2]中引入了IoU损失用于二维目标检测。不幸的是,所有这些方法都只适用于轴对齐的二维Bboxes,而不能应用于更一般的旋转Bboxes的目标检测任务。为了解决这个问题,我们首先研究了两个旋转Bbox的IoU计算,然后实现了一个统一的框架,IoU损失层用于二维和三维目标检测任务。通过将实现的 IoU损失集成到几个最先进的3D物体探测器中,在公共KITTI[3]基准上,2D检测和点云3D检测都取得了一致的改进。
- 记录这篇文章的原因,首先作者提出的iou理论上较于传统的更客观,其次他没公开源码,但是github有人进行了复现,论文中说要会提供源码这么多年了都没提供,挺难评的,但是还是感谢开源的力量,这里贴出别人非官方实现,实测代码没问题,用于学习和复现论文这篇论文还是有价值的。
引言
本文的主要贡献可以概括为:
- 我们研究了两个旋转2D和3D Bboxes的IoU损失计算;
- 我们为一般的2D和3D物体检测任务提供了一个统一的、独立于框架的IoU丢失层。
- 通过将IoU损耗层集成到几个最先进的3D物体检测框架中,如SEC-OND, PointPillars和Point R-CNN,其优势已在公共KITTI 3D物体检测基准上得到验证。
IOU

- 大多数2D检测任务都如图左边所示,通过计算得到iou配合数学函数max、min等,伪代码如下所示:轴向BBOX

旋转BBOX
- 如图的右边所示,轴向对齐的盒子并不适合在3D中表示目标物体,比如LiDAR点云中的物体,伪代码如下

IOU loss
在[1]和[2]中,IoU作为损失函数对于二维轴向BBox回归任务的有效性已经得到了很好的证明。从理论上讲,它也应该适用于旋转的BBox,因为唯一的区别是旋转的计算过程比轴对齐的计算过程更复杂。与[2]类似,我们将IoU损失定义为

针对旋转角度计算
- forward
*- 计算Bd和Bg的面积,其中Bd和Bg分别代表预测的和真实的BBox;

-
- 确定Bd与Bg相交区域的顶点,有两种方法:一种是从两个BBox的边相交,另一种是从位于另一个BBox内的BBox的角。如果顶点不存在,则IoU值为零。
-
- 理论上,这些顶点形成一个凸壳。为了计算这个凸包的面积,我们需要按照逆时针(或顺时针)的顺序对顶点进行排序。首先,计算这些顶点的中心点。然后,计算每个顶点与中心形成的旋转角度。最后,通过旋转角度对顶点进行排序。
-
- 然后,通过将其划分为小的单个三角形来获得相交面积。根据Eq.(2)计算IoU值,通过Eq.(4)计算LIoU。
补充:GIOU
作为IoU的广义版本,GIoU已在b[2]中提出,用于处理两个形状没有相交的情况。在GIoU中,给出了确定两个不相交盒体之间距离的定义。一般来说,对于任意两个凸形状A, B,最小面积边界形状C定义为:同时包围A和B的最小凸形状。通常,C应与A和B共享相同的形状类型,以便于计算。最后,式中U = AreaA + AreaB−Areaoverlap。将GIoU定义为