一、LeNets5
1. 铭记历史
1998年Yann LeCun等提出LeNets5 ,是第一个成功应用于手写数字识别问题并产生实际商业(邮政行业)价值的卷积神经网络

论文:Gradient-based learning appl ied to document re cognition
中文可参考:https://blog.csdn.net/quicmous/article/details/105730556
2. 网络模型结构
2.1 整体结构解读
一共七层,3个卷积层,2个池化层,2个全连接层
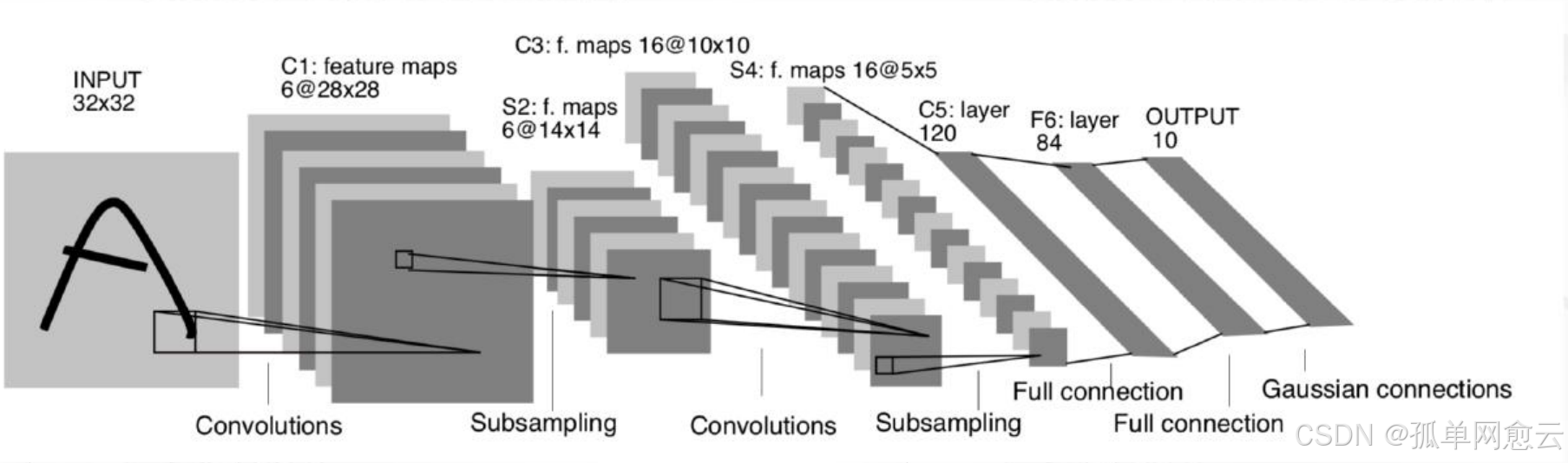
输入图像:32×32×1
三个卷积层:
C1包括6个5×5卷积核
C3包括60个5×5卷积核(通道)
C5包括120×16个5×5卷积核
两个池化层S2和S4:
都是2×2的平均池化,并添加了非线性映射
第一个全连接层:84个神经元
第二个全连接层: 10个神经元
所有激活函数采用Sigmoid
2.2 LeNets5网络细节
2.2.1 C1层-卷积层
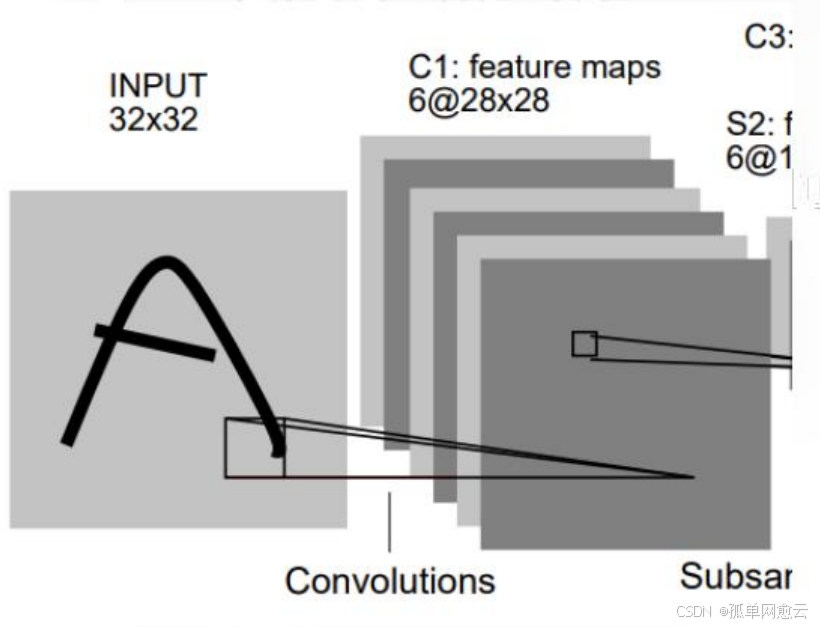
- 输入图片:32×32
- 卷积核大小:5×5
- 卷积核种类:6
- 输出特征图大小:28×28 (32-5+1)=28
- 可训练参数:(5×5+1) × 6(每个滤波器 5 ×5=25个unit参数和一个bias参数,一共6 个滤波器)
2.2.2 S2层-池化层(下采样层)
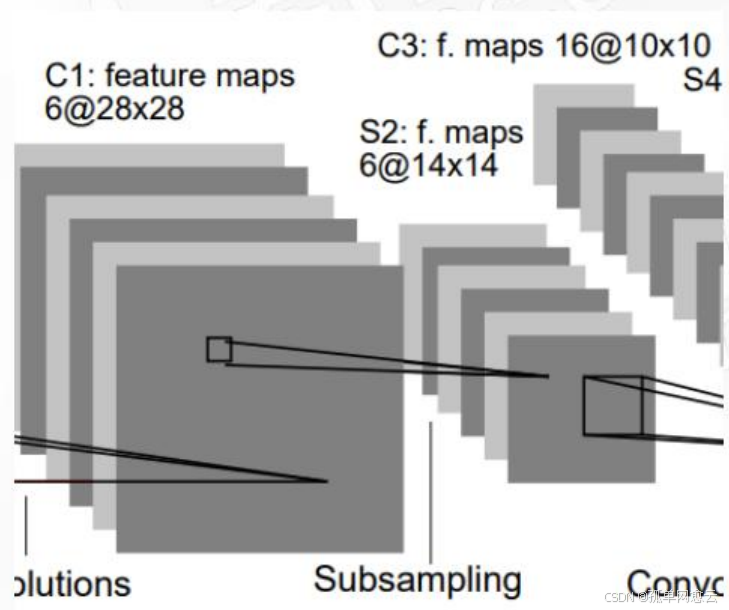
- 输入:28×28
- 采样区域:2×2
- 采样方式:输入相加,乘以一个可训练参数, 再加上一个可训练偏置,使用sigmoid激活
- 池化层实际就是一个AvgPooling,只是加了一个参数和偏执,后面的网络在池化后一般也不会激活
- 输出特征图大小:14×14(28/2)
2.2.3 C3层-卷积层
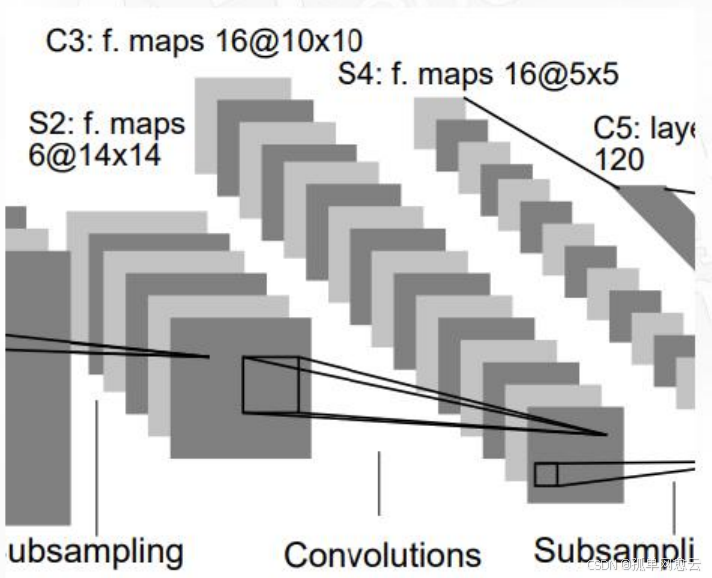
- 输入:S2中所有6个或者几个特征图组合
- 卷积核大小:5×5
- 卷积核(通道)种类:16个卷积核60个通道 :6×3 + 6×4 + 3×4 + 1×6
- 输出特征图大小:10×10 (=(14-5)/1+1)
- 可训练参数: 6×(3×5×5+1) + 6×(4×5×5+1) + 3×(4×5×5+1) + 1×(6×5×5+1)=1516
非密集的特征图连接关系
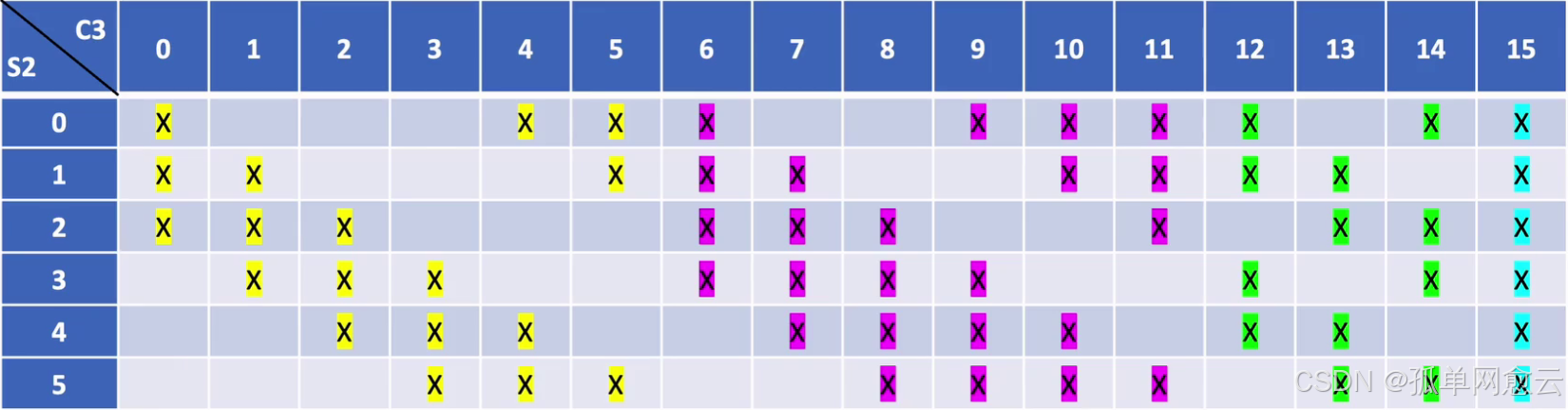
从图中可以看到:
C3的前6个特征图与S2层相连的3个特征图相连接,后面6个特征图与S2层相连的4个特征图相连 接,后面3个特征图与S2层部分不相连的4个特征图相连接,最后一个与S2层的所有特征图相连。 采用非密集连接的方式,打破对称性,同时减少计算量,共60组卷积核
2.2.4 S4层-池化层(下采样层)
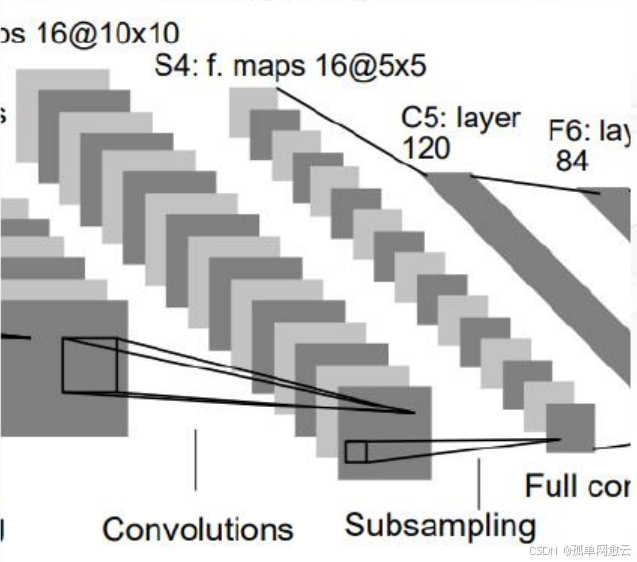
- 输入:10×10
- 采样区域:2×2
- 采样方式:输入相加,乘以一个可训练参数,再 加上一个可训练偏置,使用sigmoid激活
- 输出特征图大小:5×5(10/2)
2.2.5 C5层-卷积层
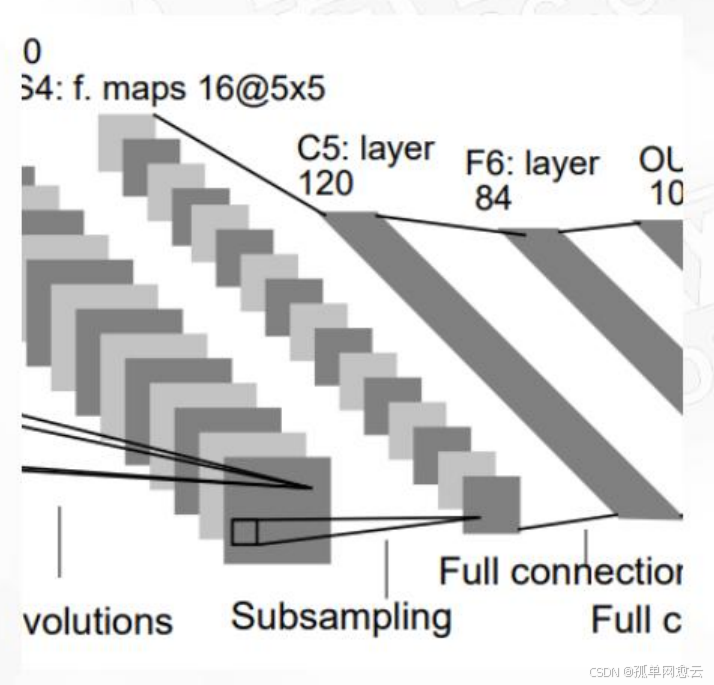
- 输入:S4层的全部16个单元特征map
- 卷积核大小:5×5
- 卷积核种类:120
- 输出特征图大小:1×1(5-5+1)
- 可训练参数/连接:120 ×(16×5×5+1)=48120
2.2.6 F6层-全连接层

- 输入:c5 120维向量
- 计算方式:计算输入向量和权重向量之间的点积,再加上一个偏置,结果通过sigmoid函数输出
- 可训练参数:84×(120+1)=10164
F6全连接层的输出设计为什么是84个节点

计算机中 字符的编码是ASCII编码,这些图是用7×12大小的位图表示, -1表示白色,1表示黑色,84可以用于对每一个像素点的 值进行估计。
2.2.7 Output层-全连接层
共有10个节点,分别代表数字0到9
y i = ∑ j ( x j − w i j ) 2 y_i=\sum_j(x_j-w_{ij})^2 yi=j∑(xj−wij)2
径向基函数(RBF)的网络连接方式,输入向量与参数向量的欧式距离。 x是激活后的输出,y是RBF的输出(误差值,最小的即为分类结果),wij是参数(人为设定的,取值-1或者1),i从0~9,j从0~83
3.网络模型实现
3.1 模型定义
python
import torch
import torch.nn as nn
# 模块的思想
class LeNet5_C3_6(nn.Module):
def __init__(self, inchannels=3, outchannels=6):
super(LeNet5_C3_6, self).__init__()
self.inchannels = inchannels
self.outchannels = outchannels
self.C3_1 = nn.ModuleList(
[
nn.Conv2d(
in_channels=self.inchannels,
out_channels=1,
kernel_size=5,
stride=1,
padding=0,
)
for i in range(outchannels)
]
)
def forward(self, x):
# 业务逻辑的实现
c3_outchannel = torch.empty(x.size(0), 0, x.size(2) - 4, x.size(3) - 4)
for i in range(self.outchannels):
# 通过这个i我们可以拿到ModuleList中的对应的卷积层
conv = self.C3_1[i]
# 拿到3输入通道 s[N, (i, (i + 3)%6), H, W] 4:0---->[4,5,0]
c_index = [j % 6 for j in range(i, i + int(self.inchannels))]
# 针对5去1的处理
if self.outchannels == 3:
# 先变成5个
c_index = [j % 6 for j in range(i, i + int(self.inchannels + 1))]
# 再去掉中间的
c_index.pop(2)
input = x[:, c_index, :, :]
# 使用卷积层对数据进行卷积操作
c3_out = conv(input)
# 拼接到总的输出通道
c3_outchannel = torch.cat((c3_outchannel, c3_out), dim=1)
return c3_outchannel
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
# 网络层
self.C1 = nn.Sequential(
nn.Conv2d(
in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=0
),
nn.ReLU(inplace=True),
)
# 自适应的做到14 * 14
self.S2 = nn.AdaptiveMaxPool2d(output_size=14)
# C3
self.C3_3_1 = LeNet5_C3_6(inchannels=3)
self.C3_4_1 = LeNet5_C3_6(inchannels=4)
self.C3_5_1 = LeNet5_C3_6(inchannels=4, outchannels=3)
self.C3_6_1 = LeNet5_C3_6(inchannels=6, outchannels=1)
# S4:自适应池化
self.S4 = nn.AdaptiveMaxPool2d(output_size=5)
# C5
self.C5 = nn.Sequential(
nn.Linear(in_features=16 * 5 * 5, out_features=120),
nn.ReLU(inplace=True),
)
self.F6 = nn.Sequential(
nn.Linear(in_features=120, out_features=84),
nn.ReLU(inplace=True),
)
# 输出层
self.Out = nn.Sequential(
nn.Linear(in_features=84, out_features=10),
nn.Softmax(dim=1)
)
def forward(self, x):
x = self.C1(x)
x = self.S2(x)
c3_outchannel_3 = self.C3_3_1(x) # 6
c3_outchannel_4 = self.C3_4_1(x) # 6
c3_outchannel_5 = self.C3_5_1(x) # 3
c3_outchannel_6 = self.C3_6_1(x) # 1
x = torch.cat(
(c3_outchannel_3, c3_outchannel_4, c3_outchannel_5, c3_outchannel_6), dim=1
)
x = nn.ReLU(inplace=True)(x)
x = self.S4(x) # N 16 5 5
x = x.view(x.size(0), -1)
x = self.C5(x)
x = self.F6(x)
x = self.Out(x)
return x
if __name__ == "__main__":
# NCHW
input = torch.randn(32, 1, 32, 32)
net = LeNet5()
# 数据交给网络进行处理
output = net(input)
print(output.shape)3.2 全局变量
python
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import os
dir = os.path.dirname(__file__)
modelpath = os.path.join(dir, "weight/model.pth")
datapath = os.path.join(dir, "data")
# 数据预处理和加载
transform = transforms.Compose(
[
transforms.Resize((32, 32)), # 调整输入图像大小为32x32
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)),
]
)3.3 模型训练
python
def train():
trainset = torchvision.datasets.MNIST(
root=datapath, train=True, download=True, transform=transform
)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=32, shuffle=True)
# 实例化模型
net = LeNet5()
# 使用MSELoss作为损失函数
criterion = nn.MSELoss()
# 使用SGD优化器
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
# 训练模型
num_epochs = 10
for epoch in range(num_epochs):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
inputs, labels = data
# 将labels转换为one-hot编码
labels_one_hot = torch.zeros(labels.size(0), 10).scatter_(
1, labels.view(-1, 1), 1.0
)
labels_one_hot = labels_one_hot.to(torch.float32)
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels_one_hot)
loss.backward()
optimizer.step()
running_loss += loss.item()
if i % 100 == 99:
print(f"[{epoch + 1}, {i + 1}] loss: {running_loss / 100:.3f}")
running_loss = 0.0
# 保存模型参数
torch.save(net.state_dict(), modelpath)
print("Finished Training")3.4 验证
python
def vaild():
testset = torchvision.datasets.MNIST(
root=datapath, train=False, download=True, transform=transform
)
testloader = torch.utils.data.DataLoader(testset, batch_size=32, shuffle=False)
# 实例化模型
net = LeNet5()
net.load_state_dict(torch.load(modelpath))
# 在测试集上测试模型
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(f"验证集: {100 * correct / total:.2f}%")