1.CW信号
CW可以叫做等幅电报,它通过电键控制发信机产生短信号"."(点)和长信号"--"(划),并利用其不同组合表示不同的字符,从而组成单词和句子。
CW信号可以看作一种幅度调制信号,类似于幅移键控(2ASK信号)其携带的信息保存在其幅度中,通过改变载波的幅度来实现基带数据的传输。
其函数表达式如下:
\[s(t) = m(t)*cos(2\pi ft + \varphi)\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space m(t) \in \left \{ 0,1\right \} \]
其中:
\(m(t)\):表示基带信号。
\(cos(2\pi ft + \varphi)\):是调制载波。
2.CW的数字正交解调
原理:
通过正交的方式即可解调出基带信号,其数学推导如下:
假设基带信号为\(m(t)\),调制的载波频率为\(f_1\),解调的载波频率为\(f_2\),相位为\(\varphi\),LPF为低通滤波器,则:
I路:
\[I(t) = LPF(s(t)*cos(2\pi f_2t + \varphi)) = LPF(m(t)*cos(2\pi f_1t) *cos(2\pi f_2t + \varphi)) \]
根据三角函数公式:
\[\begin{split} I(t) &= LPF(m(t)*cos(2\pi f_1t) *cos(2\pi f_2t + \varphi))\\ &= LPF(\frac{1}{2}m(t)*[cos(2\pi (f_1 + f_2)t+\varphi) + cos(2\pi (f_1 - f_2 )+ \varphi)]) \\ &= \frac{1}{2}m(t)*cos(2\pi (f_1 - f_2 )+ \varphi)) \\ \end{split} \]
同理:Q路:
\[\begin{split} Q(t) &= LPF(m(t)*cos(2\pi f_1t) *sin(2\pi f_2t + \varphi))\\ &= LPF(\frac{1}{2}m(t)*[cos(2\pi (f_1 + f_2)t+\varphi) - sin(2\pi (f_1 - f_2 )+ \varphi)]) \\ &= -\frac{1}{2}m(t)*sin(2\pi (f_1 - f_2 )+ \varphi)) \\ \end{split} \]
为了计算方便假设:
\[K=2\pi (f_1 - f_2 )+ \varphi \]
则:
\[\begin{split} & I(t) = \frac{1}{2}m(t)*cos(K) \\ & Q(t) = -\frac{1}{2}m(t)*sin(K) \end{split} \]
根据三角函数公式:
\[K = arctan(\frac{-Q(t)}{I(t)}) \]
注:\(arctan\)函数有作用域\((-\pi/2\space\space\space\space\pi/2)\)要求,所以将使用atan2函数替代。
\[\begin{split} & I(t) = \frac{1}{2}m(t)*cos(arctan(\frac{-Q(t)}{I(t)})) \\ & Q(t) = -\frac{1}{2}m(t)*sin(arctan(\frac{-Q(t)}{I(t)})) \end{split} \]
向量旋转,将一个向量\((cos(\theta_1),sin(\theta_1))\),逆时针旋转\(\theta_2\),旋转后的坐标为\((cos(\theta_1-\theta_2),sin(\theta_1-\theta_2))\)。将I和Q看着一个向量,将其逆时针旋转\(arctan(\frac{-Q(t)}{I(t)})\),那么:
\[\begin{split} & I'(t) = \frac{1}{2}m(t)*cos(arctan(\frac{-Q(t)}{I(t)}) - arctan(\frac{-Q(t)}{I(t)})) =\frac{1}{2}m(t)\\ & Q'(t) = -\frac{1}{2}m(t)*sin(arctan(\frac{-Q(t)}{I(t)}) - arctan(\frac{-Q(t)}{I(t)})) = 0 \end{split} \]
这样就消除了相位差和频率差带来的误差,\(I'(t)\)就是我们解调的结果。其结果与频率差与相位差无关。
3.拍频信号
看过电视剧里面发电报的应该不陌生,电台在发出或者接收电台信号的时候,经常会听到滴滴答答的声音,CW信号如何转化为音频信号,就需要通过拍频器来完成,将电信号转化为人耳可以识别的声音信号频率(20-20000Hz),通过扬声器播放。
4.MATLAB仿真
仿真代码:
matlab
close all;
fs = 100E3;%采样率
base_data = [1,0,0,1,0,1,0,0,0,1,1,0,0,1,0];
len = 1E3;
mt = interp1((1:length(base_data)), base_data, (0:length(base_data)/len:length(base_data)-length(base_data)/len), 'nearest');
f_carr_1 = 20E3;%调制载波频率
f_carr_2 = 21E3;%解调载波频率
fi = 0.2;%解调载波初始相位
t = 0:1/fs:(len-1)/fs;
cw_data = mt.*cos(2*pi*f_carr_1*t);
I = mt.*cos(2*pi*(f_carr_1-f_carr_2)*t-fi)/2 + randn(size(t))/1000;
Q = -mt.*sin(2*pi*(f_carr_1-f_carr_2)*t-fi)/2 + randn(size(t))/1000;
%% 向量旋转
theta0 = atan2(Q./(-mt),I./(mt));
It0 = I.*cos(theta0) - Q.*sin(theta0);
Qt0 = Q.*cos(theta0) + I.*sin(theta0);
f_p = 4E3;%拍频频率
theta1 = (0:1:length(I)-1)*(f_p*(2*pi)/fs);
It1 = It0.*cos(theta1) ;
%% 保存IQ数据FPGA使用仿真
% fid = fopen('CW.txt','w');
% for i = 1:l
% fprintf(fid,'%d %d\n',floor(I(i)* (2^13)),floor(Q(i)* (2^13)));
% end
% fclose(fid);
%% 绘制
figure
time = 6;
subplot(time,1,1);
plot(mt);
title('基带数据');
subplot(time,1,2);
plot(cw_data);
title('调制数据');
subplot(time,1,3);
plot(I);
title('I路');
subplot(time,1,4);
plot(Q);
title('Q路');
subplot(time,1,5);
plot(It0);
title('解调数据');
subplot(time,1,6);
plot(It1);
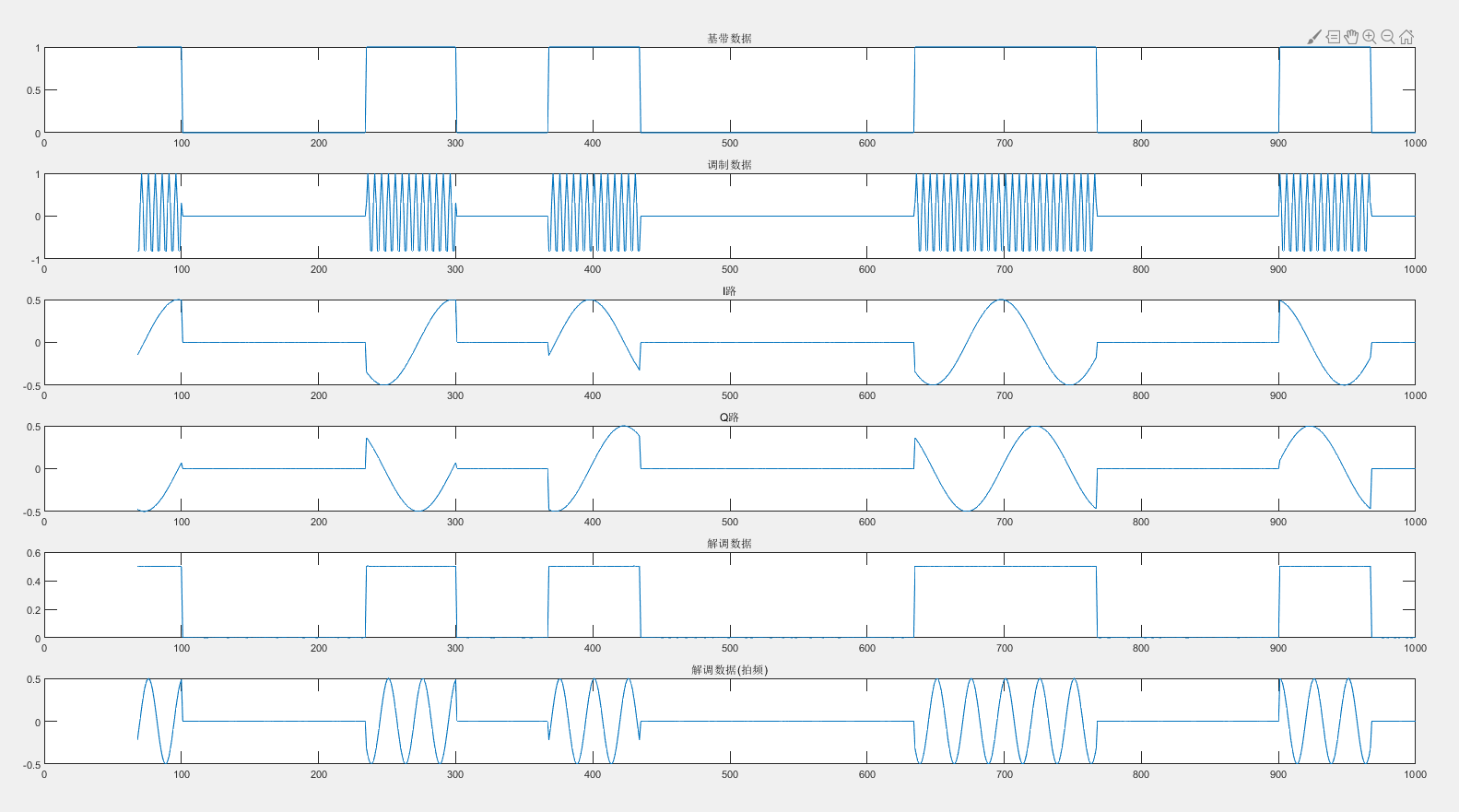
title('解调数据(拍频)');结果:
4.FPGA解调
有空补上