NLP中的神经网络基础

一：多层感知器模型

1：感知器

解释一下，为什么写成 wx+b>0 ，其实原本是 wx > t ,t就是阈值，超过这个阈值fx就为1，现在把t放在左边。

在感知器里面涉及到两个问题：

第一个，特征提取：就是如何将问题的原始输入转换成输入向量x（其实就是数值如何表示文本）

第二个，参数学习（参数优化或者模型训练）：就是如何设置合理的w权重和b偏差项

感知器主要处理文本分类问题，比如识别一个句子的褒贬性。

2：线性回归

感知器输出的结果是离散的，除了感知器这类分类模型还有一类是回归模型（Regression），他的输出是连续的实数值。线性回归是最简单的回归模型。y = wx + b

3：Logical回归

线性回归的输出值大小是任意的，激活函数就是为了将其限制在一定的范围内。

Logical函数形式为：

其中，k控制了函数的陡峭程度。

如果 ，此时的模型叫做Logical回归模型。虽然叫做回归模型但是常用作分类问题。

原因：当L=1、k=1，z0 = 0 ，此时函数形式就是sigmoid函数

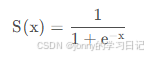
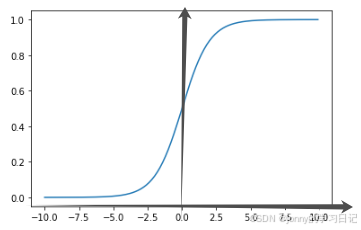
它的值域恰好在0-1，所以经过sigmoid函数归一化以后就可以认为是输入属于某一类别的概率值，除了可以输出概率值还有一个优点就是它的导数比较容易求得，有利于使用基于梯度的参数优化算法。sigmoid函数图像如下图：

4：Softmax回归

如果不只有2个类别，处理多元分类任务可以用Softmax回归操作。

Softmax回归就是对第i个类别使用线性回归打一个分数。其中，表示第i个类别对应的第i个输入的权重。然后再对多个分数使用指数函数进行归一化计算，并获得一个输入属于某个类别的概率。

5：多层感知器（MLP）

以上介绍的都是线性模型，真实情况很多时候无法通过一条直线、平面、或者超平面来分割不同的类别，例如：异或问题（相同为0，不同为1）

多层感知器 就是堆叠多层线性分类器 ，并在中间（隐含层）增加非线性激活函数。

常见激活函数可以参考：常见激活函数（Sigmoid、Tanh、Relu、Leaky Relu、Softmax）_sigmoid激活函数-CSDN博客

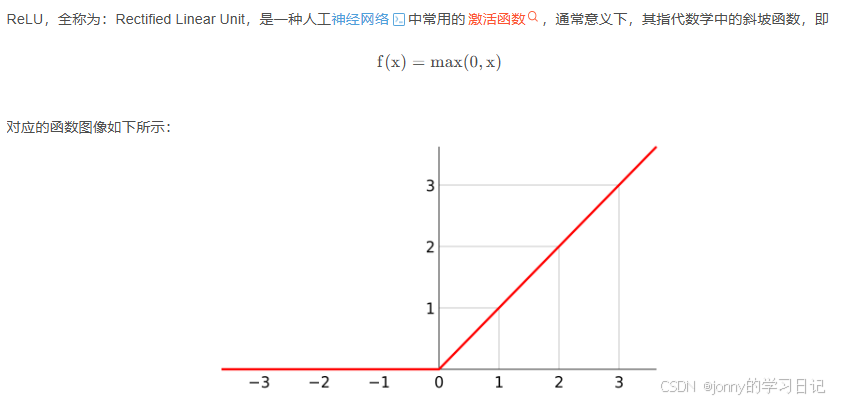
ReLU：

6：模型实现

（1）：神经网络层和激活函数

线性层：输入为（batch，inputdim）输出为（batch，outputdim）

# 线性层
import torch
from torch import nn
linear = nn.Linear(32, 2)   # 第一个参数就是输入，第二个是输出
inputs = torch.rand(3, 32)  # 创建一个输入为3， 23 维度的随机张量  可以理解为3是batch
outputs = linear(inputs)
print("Linear:")
print(outputs)

batch就是一个批次，即为一次处理的张量数量。

这里grad_fn是张量（tensor）的一个属性，它记录了创建该张量的函数操作。

激活函数在torch.nn.functional中

# 线性层
import torch
from torch import nn
linear = nn.Linear(32, 2)   # 第一个参数就是输入，第二个是输出
inputs = torch.rand(3, 32)  # 创建一个输入为3， 23 维度的随机张量  可以将3理解为batch
outputs = linear(inputs)
print("Linear:")
print(outputs)
print("*****"*20)


from torch.nn import functional as F
activation_sigmoid = F.sigmoid(outputs)
print("activation_sigmoid:")
print(activation_sigmoid)
print("*****"*20)

activation_softmax = F.softmax(outputs)
print("activation_softmax:")
print(activation_softmax)
print("*****"*20)

activation_relu = F.relu(outputs)
print("activation_relu:")
print(activation_relu)
print("*****"*20)

activation_tanh = F.tanh(outputs)
print("activation_tanh:")
print(activation_tanh)
print("*****"*20)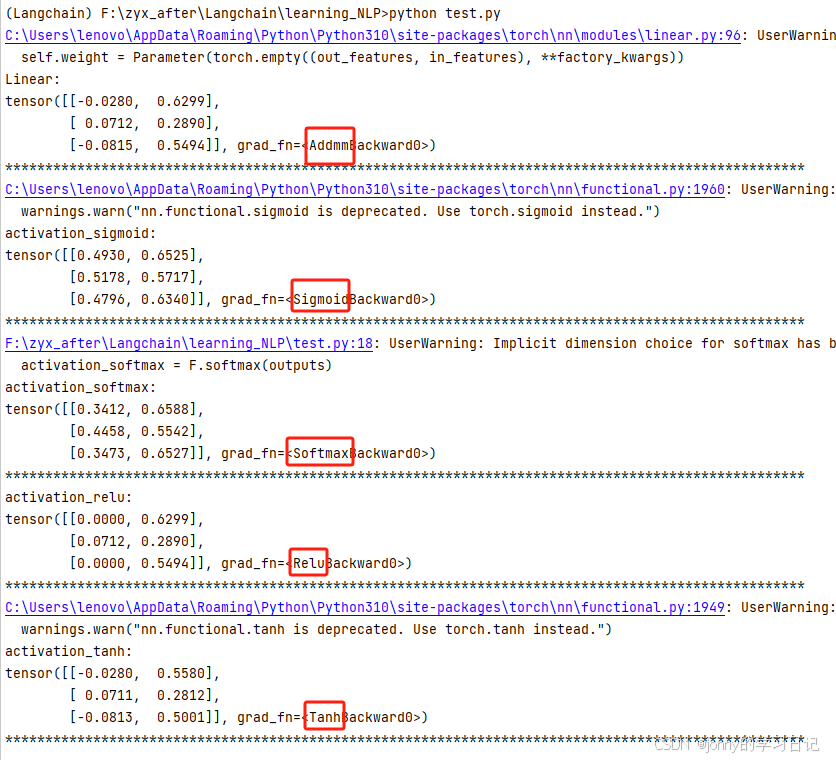

（2）：自定义神经网络模型

import torch
from torch import nn
from torch.nn import functional as F

class MLP(nn.Module):
    # 多层感知器的构建
    def __init__(self, input_dim, hidden_dim, num_class):
        super(MLP, self).__init__()
        # 线性变换：输入层-->隐含层
        self.linear1 = nn.Linear(input_dim, hidden_dim)

        # ReLU
        self.activate = F.relu

        # 线性变换：隐藏层-->输出层
        self.linear2 = nn.Linear(hidden_dim, num_class)

    def forward(self, inputs):
        hidden = self.linear1(inputs)
        activation = self.activate(hidden)
        outputs = self.linear2(activation)
        probs = F.softmax(outputs, dim=1)  # 获得每个输入属于某一类别的概率
        return probs


mlp = MLP(input_dim=4, hidden_dim=5, num_class=2)
inputs = torch.rand(3, 4)
probs = mlp(inputs)
print(probs)

---

二：卷积神经网络（CNN）

1：模型结构

全连接层：又叫做稠密层，在多层感知器中每层输入的各个元素都需要乘以一个独立的参数的那一层叫做全连接层。 缺点：难以捕捉局部信息。

卷积 操作：就是依次扫描输入的每个区域。每个小的、用于提取局部特征的稠密层被叫做卷积核或者滤波器。假设卷积核的大小为N，单词长度为L，那么卷积核的输出长度为L-N+1

卷积操作输出的结果再进行进一步聚合，这一过程就是**池化。**池化包括最大池化、平均池化、加和池化等。池化的优点：解决样本输入大小不一致的问题；可以保证最终输出相同个数的特征。

卷积核的构造方式大致有两种：a：使用不同组的参数，且不同的初始化参数获得不同的卷积核。b：提取不同尺度的局部特征（例如：提取不同大小N-gram）

卷积操作以后再经过一个全连接的分类层 就可以做出最终的决策。将多个卷积层池化层叠堆叠起来形成更深层次的网络就叫做卷积神经网络（CNN）。

输入+卷积+池化+全连接

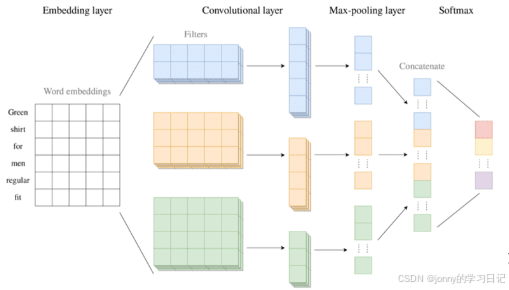
前馈神经网络：信息从输入层经过隐藏层再到输出层，按照一个方向流动，就叫做前馈神经网络

2：模型实现

import torch
from torch.nn import Conv1d

# 卷积操作调用
conv1 = Conv1d(5, 2, 4)  # 通道大小为5 输出通道大小为2 卷积核宽度为4
conv2 = Conv1d(5, 2, 3)

inputs = torch.rand(2, 5, 6)  # 输入批次为2 每个序列长度为6 每个输入的维度是5

outputs1 = conv1(inputs)
outputs2 = conv2(inputs)

print("outputs1:")
print(outputs1)
print(type(outputs1))  # 2 2 3
print(outputs1.shape)
print("*****"*20)
print("outputs2:")
print(outputs2)
print(outputs2.shape)  # 2 2 4
print("*****"*20)


# 池化操作调用
from torch.nn import MaxPool1d

pool1 = MaxPool1d(3)  # 池化层核大小为3 即为卷积层的输出序列长度
pool2 =  MaxPool1d(4)

outputs_pool1 = pool1(outputs1)
outputs_pool2 = pool2(outputs2)

print("outputs_pool1:")
print(outputs_pool1)
print(type(outputs_pool1))
print(outputs_pool1.shape)  # 2 2 1
print("*****"*20)
print("outputs_pool2:")
print(outputs_pool2)
print(outputs_pool2.shape)  # 2 2 1
print("*****"*20)


# 将两个池化后的张量合在一起
outputs_pool_squeeze1 = outputs_pool1.squeeze(dim=2)  # 去掉最后一个维度  2 2
outputs_pool_squeeze2 = outputs_pool2.squeeze(dim=2)  # 2 2
outputs_pool = torch.cat([outputs_pool_squeeze1, outputs_pool_squeeze2], dim=1)  # 变为 2 4

# 最后全连接层
from torch.nn import Linear
linear = Linear(4, 2)
outputs_linear = linear(outputs_pool)
print("outputs_linear:")
print(outputs_linear)
print(outputs_linear.shape)  # 2 2
print("*****"*20)

注意维度变化

---

三：循环神经网络（RNN）

多层感知器和卷积神经网络信息都是按照一个方向流动，因此都属于前馈神经网络，下面介绍信息循环流动的网络。

1：模型结构

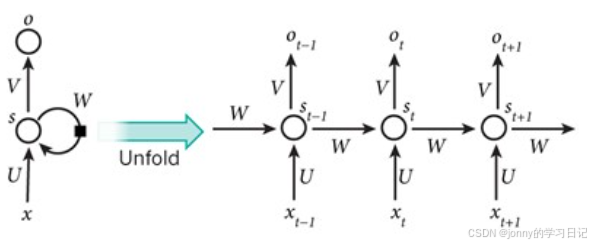
循环神经网络，将其展开后就相当于堆叠多个共享隐藏层参数的前馈神经网络。隐藏层更新的方式可以用以下的公式进行表达：

其中，

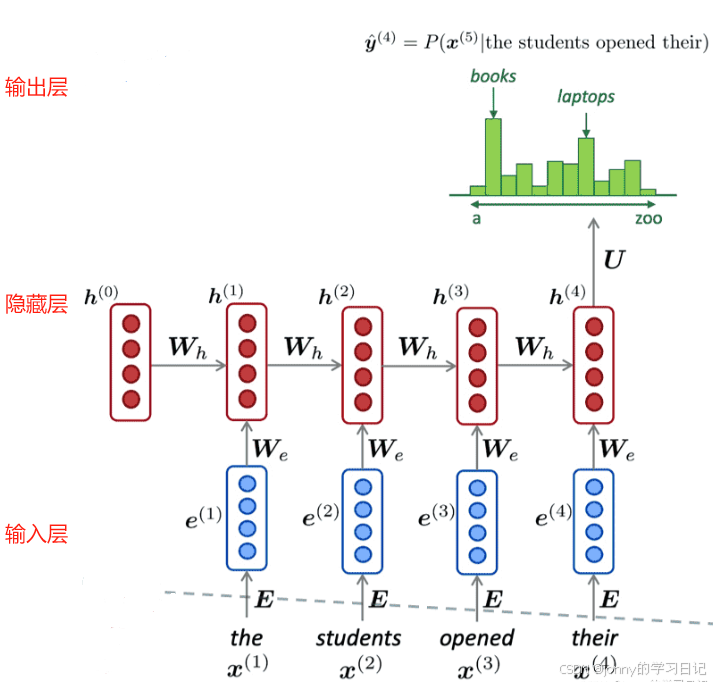
每个时刻的隐藏层 h(t) 承载了 1~t 时刻的全部信息，因此循环神经网络中的隐藏层也被称为记忆单元。

2：长短记忆网络

长短记忆网络将隐藏层的更新方式改为

但是，可能要考虑两个状态的比率，所以需要添加一个 ft 系数来控制加权（遗忘门）

就可以将公式改为

但是，如果两种状态需要独立的话，就需要使用独立的系数来控制。这里的it系数就叫做输入门

同样，还可以增加输出门控制机制

这里的ct被叫做记忆细胞。

3：模型实现

from torch.nn import RNN
import torch

rnn = RNN(input_size=4, hidden_size=5, batch_first=True)  # 每个时刻输出大小为 4 隐藏层大小为 5 batch_first代表第一个是否为batch
inputs = torch.rand(2, 3, 4)
outputs, hn = rnn(inputs)

print("outputs:")
print(outputs)
print(type(outputs))  # 2 2 3
print(outputs.shape)
print("*****"*20)

print("hn:")
print(hn)
print(type(hn))  # 2 2 3
print(hn.shape)
print("*****"*20

四：注意力模型

---

五：神经网络模型的训练

---

未完待续。。。。持续更新