真实数据集
引言
在实践中,深度学习通常涉及庞大的数据集(通常以TB甚至更多为单位),模型的训练可能需要数天、数周甚至数月。这就是为什么到目前为止,我们使用了程序生成的数据集来使学习过程更易管理并保持快速,同时学习深度学习的数学和其他相关方面的知识。本书的主要目标是教授神经网络的工作原理,而不是深度学习在各种问题中的应用。话虽如此,现在我们将探索一个更实际的数据集,因为这将带来一些我们尚未考虑的深度学习新挑战。
如果你在阅读本书之前已经探索过深度学习,你可能已经熟悉(也可能感到厌倦)MNIST数据集,这是一个包含手写数字(0到9)的图像数据集,每张图像的分辨率为28x28像素。它是一个相对较小的数据集,对模型来说也相对容易学习。这个数据集曾成为深度学习的"Hello World",并且一度是机器学习算法的基准。然而,这个数据集的问题在于,获得99%以上的准确率变得极其容易,因此它无法提供足够的空间来学习各种参数如何影响模型的学习过程。然而,在2017年,一家名为Zalando的公司发布了一个名为Fashion MNIST的数据集(https://arxiv.org/abs/1708.07747),这是MNIST数据集的直接替代品(https://github.com/zalandoresearch/fashion-mnist)。
Fashion MNIST数据集包含60,000个训练样本和10,000个测试样本,这些样本是28x28像素的图像,涵盖了10种不同的服装类别,例如鞋子、靴子、衬衫、包等。我们稍后会看到一些示例,但首先我们需要获取实际的数据。由于原始数据集由包含特定格式编码图像数据的二进制文件组成,为了本书的使用,我们已经准备并托管了一个预处理数据集,其中包含以.png格式保存的图像。通常,对于图像来说,使用无损压缩是明智的,因为有损压缩(例如JPEG)会通过更改图像数据对图像造成影响。这些图像还根据标签分组,并被分成训练组和测试组。样本是服装物品的图像,而标签是分类信息。以下是数字标签及其对应的描述:
数据准备
首先,我们将从nnfs.io网站获取数据。让我们定义数据集的URL、本地保存的文件名以及解压图像的文件夹:
python
URL = 'https://nnfs.io/datasets/fashion_mnist_images.zip'
FILE = 'fashion_mnist_images.zip'
FOLDER = 'fashion_mnist_images'接下来,使用Python的标准库urllib下载压缩数据(如果指定路径下的文件不存在):
python
import os
import urllib
import urllib.request
if not os.path.isfile(FILE):
print(f'Downloading {URL} and saving as {FILE}...')
urllib.request.urlretrieve(URL, FILE)接下来,我们将使用另一个标准的Python库zipfile来解压文件。我们会使用上下文管理器(即with关键字,它会为我们打开和关闭文件)来获取压缩文件的句柄,并使用.extractall方法和指定的FOLDER提取所有包含的文件:
python
from zipfile import ZipFile
print('Unzipping images...')
with ZipFile(FILE) as zip_images:
zip_images.extractall(FOLDER)检索数据的完整代码:
python
from zipfile import ZipFile
import os
import urllib
import urllib.request
URL = 'https://nnfs.io/datasets/fashion_mnist_images.zip'
FILE = 'fashion_mnist_images.zip'
FOLDER = 'fashion_mnist_images'
if not os.path.isfile(FILE):
print(f'Downloading {URL} and saving as {FILE}...')
urllib.request.urlretrieve(URL, FILE)
print('Unzipping images...')
with ZipFile(FILE) as zip_images:
zip_images.extractall(FOLDER)
print('Done!')运行:
python
>>>
Downloading https://nnfs.io/datasets/fashion_mnist_images.zip and saving as fashion_mnist_images.zip...
Unzipping images...
Done!现在你应该有一个名为fashion_mnist_images的目录,其中包含test和train目录以及数据许可文件。在test和train目录中各有10个子目录,编号从0到9。这些数字是与其中图像对应的分类。例如,如果我们打开目录0,可以看到这些是短袖或无袖衬衫的图像。例如:

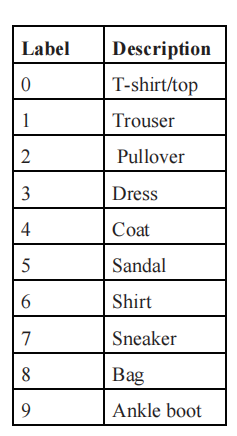
在目录 7 中,我们有非靴子鞋,或本数据集创建者分类的运动鞋。例如:

将图像转换为灰度图(即将每像素的三通道RGB值转换为单一的黑白范围,像素值为0到255)是一种常见的做法,不过这些图像已经是灰度图。另外,将图像调整大小以规范其尺寸也是一种常见的做法,但同样地,Fashion MNIST数据集已经经过处理,所有图像的尺寸都相同(28x28)。
数据加载
接下来,我们需要将这些图像读入Python,并将图像(像素)数据与相应的标签关联起来。我们可以通过以下方式访问这些目录:
python
import os
labels = os.listdir('fashion_mnist_images/train')
print(labels)
python
>>>
['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']由于子目录名称本身就是标签,我们可以通过查看每个编号子目录中的文件来引用每个类别的单个样本:
python
files = os.listdir('fashion_mnist_images/train/0')
print(files[:10])
print(len(files))
python
>>>
['0000.png', '0001.png', '0002.png', '0003.png', '0004.png', '0005.png', '0006.png', '0007.png', '0008.png', '0009.png']
6000如你所见,我们有6,000个类别0的样本。总共我们有60,000个样本,每个类别6,000个。这意味着我们的数据集已经是平衡的;每个类别出现的频率相同。如果数据集未平衡,神经网络可能会倾向于预测包含最多图像的类别。这是因为神经网络本质上会寻找最陡峭且最快的梯度下降以减少损失,这可能导致陷入局部最小值,使模型无法找到全局损失的最小值。我们这里总共有10个类别,因此在一个平衡的数据集中,随机预测的准确率大约为10%。
然而,假设数据集中类别的不平衡程度为类别0占64%,而类别1到9分别仅占4%。神经网络可能会很快学会始终预测类别0。尽管模型的损失最初会迅速降低,但它可能会一直停留在预测类别0上,准确率接近64%。在这种情况下,我们最好通过削减高频类别的样本数量,使每个类别的样本数量相同。
另一个选择是使用类别权重,在计算损失时为频率较高的类别赋予小于1的权重。然而,在实践中我们几乎没有见过这种方法效果很好。对于图像数据,另一个选择是通过裁剪、旋转、水平或垂直翻转等操作来扩充样本。在应用这些变换之前,需确保它们会生成符合目标的有效样本。幸运的是,我们无需担心这一点,因为Fashion MNIST数据集已经完全平衡。现在,我们将通过查看单个样本来探索数据。为处理图像数据,我们将使用包含OpenCV的Python包,即cv2库,你可以通过pip/pip3安装它:
python
pip3 install opencv-python并加载图像数据:
python
import cv2
image_data = cv2.imread('fashion_mnist_images/train/7/0002.png', cv2.IMREAD_UNCHANGED)
print(image_data)我们使用cv2.imread()读取图像,其中第一个参数是图像的路径。参数cv2.IMREAD_UNCHANGED通知cv2包,我们希望以图像保存时的格式读取它们(在这种情况下是灰度图)。默认情况下,即使是灰度图,OpenCV也会将这些图像转换为使用所有三个颜色通道。因此,我们得到的是一个二维数组------灰度像素值。如果我们在打印之前使用以下代码行格式化这个杂乱的数组,NumPy会知道打印更多的字符在一行中,因为加载的图像是一个NumPy数组对象:
python
import numpy as np
np.set_printoptions(linewidth=200)我们仍然可能能够识别出主题:
python
>>>
[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 49 135 182 150 59 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 78 255 220 212 219 255 246 191 155 87 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 57 206 215 203 191 203 212 216 217 220 211 15 0]
[ 0 0 0 0 0 0 0 0 0 0 1 0 0 0 58 231 220 210 199 209 218 218 217 208 200 215 56 0]
[ 0 0 0 0 1 2 0 0 4 0 0 0 0 145 213 207 199 187 203 210 216 217 215 215 206 215 130 0]
[ 0 0 0 0 1 2 4 0 0 0 3 105 225 205 190 201 210 214 213 215 215 212 211 208 205 207 218 0]
[ 1 5 7 0 0 0 0 0 52 162 217 189 174 157 187 198 202 217 220 223 224 222 217 211 217 201 247 65]
[ 0 0 0 0 0 0 21 72 185 189 171 171 185 203 200 207 208 209 214 219 222 222 224 215 218 211 212 148]
[ 0 70 114 129 145 159 179 196 172 176 185 196 199 206 201 210 212 213 216 218 219 217 212 207 208 200 198 173]
[ 0 122 158 184 194 192 193 196 203 209 211 211 215 218 221 222 226 227 227 226 226 223 222 216 211 208 216 185]
[ 21 0 0 12 48 82 123 152 170 184 195 211 225 232 233 237 242 242 240 240 238 236 222 209 200 193 185 106]
[ 26 47 54 18 5 0 0 0 0 0 0 0 0 0 2 4 6 9 9 8 9 6 6 4 2 0 0 0]
[ 0 10 27 45 55 59 57 50 44 51 58 62 65 56 54 57 59 61 60 63 68 67 66 73 77 74 65 39]
[ 0 0 0 0 4 9 18 23 26 25 23 25 29 37 38 37 39 36 29 31 33 34 28 24 20 14 7 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]在这种情况下,这是一个运动鞋。与其通过格式化原始值来查看图像,我们可以使用Matplotlib来可视化它。例如:
python
import matplotlib.pyplot as plt
plt.imshow(image_data)
plt.show()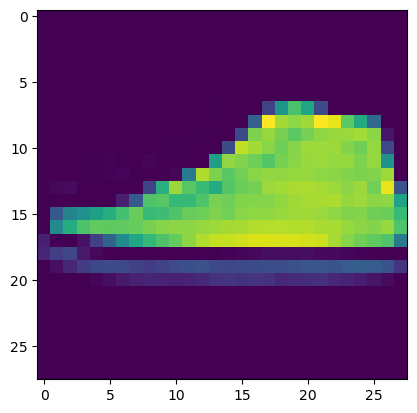
我们可以检查另一个样本:
python
import matplotlib.pyplot as plt
image_data = cv2.imread('fashion_mnist_images/train/4/0011.png', cv2.IMREAD_UNCHANGED)
plt.imshow(image_data)
plt.show()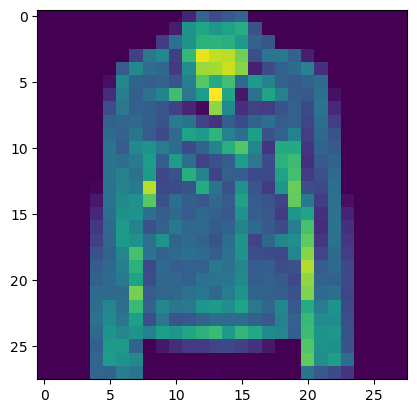
看起来像是一件夹克。如果我们查看之前的表格,类别4是"外套"。你可能会对奇怪的颜色感到疑惑,但这只是因为Matplotlib默认不期望灰度图像。我们可以在调用plt.imshow()时通过指定cmap(颜色映射)来通知Matplotlib这是灰度图像:
python
import matplotlib.pyplot as plt
image_data = cv2.imread('fashion_mnist_images/train/4/0011.png', cv2.IMREAD_UNCHANGED)
plt.imshow(image_data, cmap='gray')
plt.show()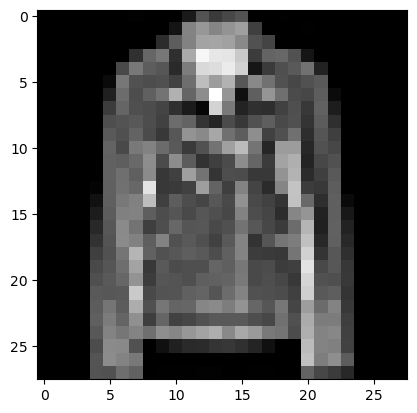
现在我们可以遍历所有样本,将它们加载到输入数据( X X X)和目标( y y y)列表中。首先,我们扫描训练文件夹,正如之前提到的,该文件夹包含从0到9命名的子文件夹,这些子文件夹同时也充当样本标签。我们遍历这些文件夹及其中的图像,将图像添加到一个列表变量(命名为 X X X)中,并将其对应的标签添加到另一个列表变量(命名为 y y y)中,从而形成我们的样本和真实标签(目标标签):
python
# Scan all the directories and create a list of labels
labels = os.listdir('fashion_mnist_images/train')
# Create lists for samples and labels
X = []
y = []
# For each label folder
for label in labels:
# And for each image in given folder
for file in os.listdir(os.path.join('fashion_mnist_images', 'train', label)):
# Read the image
image = cv2.imread(os.path.join('fashion_mnist_images/train', label, file), cv2.IMREAD_UNCHANGED)
# And append it and a label to the lists
X.append(image)
y.append(label)我们需要对测试数据和训练数据执行相同的操作。幸运的是,它们已经为我们很好地分开了。很多时候,你需要自己将数据分成训练组和测试组。我们将把上述代码转换为一个函数,以避免为训练和测试目录重复编写代码。这个函数将接收一个数据集类型(训练或测试)作为参数,以及这些数据集所在路径:
python
import numpy as np
import cv2
import os
# Loads a MNIST dataset
def load_mnist_dataset(dataset, path):
# Scan all the directories and create a list of labels
labels = os.listdir(os.path.join(path, dataset))
# Create lists for samples and labels
X = []
y = []
# For each label folder
for label in labels:
# And for each image in given folder
for file in os.listdir(os.path.join(path, dataset, label)):
# Read the image
image = cv2.imread(os.path.join(path, dataset, label, file), cv2.IMREAD_UNCHANGED)
# And append it and a label to the lists
X.append(image)
y.append(label)
# Convert the data to proper numpy arrays and return
return np.array(X), np.array(y).astype('uint8')由于 X X X被定义为一个列表,并且我们将以NumPy数组形式表示的图像添加到这个列表中,因此我们会在最后调用np.array()将 X X X从列表转换为一个正式的NumPy数组。对于标签( y y y)也会执行相同的操作,因为它们是一个数字列表,我们还需要告知NumPy这些标签是整数(而非浮点数)值。
然后,我们可以编写一个函数,用于创建并返回我们的训练和测试数据:
python
# MNIST dataset (train + test)
def create_data_mnist(path):
# Load both sets separately
X, y = load_mnist_dataset('train', path)
X_test, y_test = load_mnist_dataset('test', path)
# And return all the data
return X, y, X_test, y_test到目前为止,针对我们新数据的代码:
python
import numpy as np
import cv2
import os
# Loads a MNIST dataset
def load_mnist_dataset(dataset, path):
# Scan all the directories and create a list of labels
labels = os.listdir(os.path.join(path, dataset))
# Create lists for samples and labels
X = []
y = []
# For each label folder
for label in labels:
# And for each image in given folder
for file in os.listdir(os.path.join(path, dataset, label)):
# Read the image
image = cv2.imread(os.path.join(path, dataset, label, file), cv2.IMREAD_UNCHANGED)
# And append it and a label to the lists
X.append(image)
y.append(label)
# Convert the data to proper numpy arrays and return
return np.array(X), np.array(y).astype('uint8')
# MNIST dataset (train + test)
def create_data_mnist(path):
# Load both sets separately
X, y = load_mnist_dataset('train', path)
X_test, y_test = load_mnist_dataset('test', path)
# And return all the data
return X, y, X_test, y_test有了这个函数,我们就可以通过以下操作加载数据:
python
# Create dataset
X, y, X_test, y_test = create_data_mnist('fashion_mnist_images')数据预处理
接下来,我们将对数据进行缩放(不是对图像本身,而是表示它们的数字)。神经网络在数据范围为0到1或-1到1时通常表现最佳。在这里,图像数据的范围是0到255。我们需要决定如何对这些数据进行缩放。通常,这一过程需要一些实验和反复试验。例如,我们可以将图像缩放到-1到1的范围,通过对每个像素值减去所有像素值的最大值的一半(即 255 / 2 = 127.5 255/2 = 127.5 255/2=127.5),然后除以这一半,从而生成一个范围为-1到1的值。我们也可以通过简单地将数据除以255(最大值)将其缩放到0到1的范围。首先,我们选择将数据缩放到-1到1的范围。在执行这一操作之前,我们需要更改NumPy数组的数据类型,当前的数据类型是uint8(无符号整数,范围为0到255的整数值)。如果我们不更改,NumPy会将其转换为float64数据类型,而我们的目的是使用float32(32位浮点值)。可以通过在NumPy数组对象上调用.astype(np.float32)实现。标签将保持不变:
python
# Create dataset
X, y, X_test, y_test = create_data_mnist('fashion_mnist_images')
# Scale features
X = (X.astype(np.float32) - 127.5) / 127.5
X_test = (X_test.astype(np.float32) - 127.5) / 127.5确保使用相同的方法对训练数据和测试数据进行缩放。稍后,在进行预测时,你还需要对用于推断的输入数据进行缩放。在不同的地方忘记对数据进行缩放是很常见的错误。同时,你需要确保任何预处理操作(例如缩放)仅基于训练数据集的信息。在这个例子中,我们知道最小值(min)和最大值(max)分别为0和255,并执行了线性缩放。然而,通常你需要首先查询数据集的最小值和最大值以用于缩放。如果你的数据集中存在极端异常值,最小/最大值方法可能效果不佳。在这种情况下,你可以使用平均值和标准差的某种组合来创建缩放方法。
缩放时一个常见的错误是允许测试数据集影响对训练数据集所做的变换。对此规则唯一的例外是当数据以线性方式缩放,例如通过提到的除以常数的方式。如果使用的是非线性缩放函数,可能会将测试或验证数据的信息泄露到训练数据中。任何预处理规则都应该在不了解测试数据集的情况下得出,但随后应用于测试数据集。例如,你的整个数据集可能最小值为0,最大值为125,而训练数据集的最小值为0,最大值为100。在这种情况下,你仍然会使用100作为缩放测试数据集的值。这意味着你的测试数据集在缩放后可能不会完全适合-1到1的范围,但这通常不是问题。如果差异较大,你可以通过将数据线性缩放再除以某个数值来进行额外的缩放。
回到我们的数据,让我们检查一下数据是否已经缩放:
python
print(X.min(), X.max())
python
>>>
-1.0 1.0接下来,我们检查输入数据的形状:
python
print(X.shape)
python
>>>
(60000, 28, 28)我们的Dense层处理的是一维向量的批量数据,无法直接操作形状为28x28的二维数组图像。我们需要将这些28x28的图像"展平",这意味着将图像数组的每一行依次附加到数组的第一行,从而将图像的二维数组转换为一维数组(即向量)。换句话说,这可以看作是将二维数组中的数字展开为类似列表的形式。有一种叫做卷积神经网络的模型,可以直接处理二维图像数据,但像我们这里的全连接神经网络(Dense网络)需要一维的样本数据。即使在卷积神经网络中,你通常也需要在将数据传递到输出层或Dense层之前对数据进行展平。
在NumPy中展平数组可以使用reshape方法,并将第一个维度设置为-1,表示"根据实际元素数量决定",从而将所有元素放在第一维度中,形成一个一维数组。以下是这种概念的一个示例:
python
example = np.array([[1,2],[3,4]])
flattened = example.reshape(-1)
print(example)
print(example.shape)
print(flattened)
print(flattened.shape)
python
>>>
[[1 2]
[3 4]]
(2, 2)
[1 2 3 4]
(4,)我们也可以使用np.flatten()方法,但当处理一批样本时,我们的意图有所不同。在样本的情况下,我们希望保留所有60,000个样本,因此我们需要将训练数据的形状调整为(60000, -1)。这将通知NumPy我们希望保留60,000个样本(第一维度),但将其余的部分展平(-1作为第二维度意味着我们希望将所有样本数据放入这个单一维度中,形成一维数组)。这将创建60,000个样本,每个样本包含784个特征。这784个特征是28·28的结果。为此,我们将分别使用训练数据(X.shape[0])和测试数据(X_test.shape[0])的样本数量,并对它们进行reshape操作:
python
# Reshape to vectors
X = X.reshape(X.shape[0], -1)
X_test = X_test.reshape(X_test.shape[0], -1)你也可以通过显式定义形状来实现相同的结果,而不是依赖NumPy的推断:
python
.reshape(X.shape[0], X.shape[1]*X.shape[2])这样会更明确,但我们认为这样不太清晰。
数据洗牌
我们当前的数据集由样本及其目标分类组成,按顺序从0到9排列。为了说明这一点,我们可以在不同位置查询 y y y数据。前6000个样本的标签都将是0。例如:
python
print(y[0:10])
python
>>>
[0 0 0 0 0 0 0 0 0 0]如果我们稍后再进行查询:
python
print(y[6000:6010])
python
>>>
[1 1 1 1 1 1 1 1 1 1]如果我们按这种顺序训练网络,会导致问题;原因与数据集不平衡的问题类似。
在训练前6,000个样本时,模型会学到最快减少损失的方法是始终预测为0,因为它会看到多个仅包含类别0的数据批次。然后,在6,000到12,000之间,损失会因为标签的变化而最初上升,而模型仍然会错误地预测标签为0。随后,模型可能会学到现在需要始终预测类别1(因为它在优化过程中看到的标签批次全是类别1)。模型会在当前批次中重复的标签附近循环于局部最小值,并且很可能永远找不到全局最小值。这一过程会一直持续,直到我们完成所有样本,并重复我们选择的训练轮数(epochs)。
理想情况下,每次拟合的样本中应该包含多个类别(最好每个类别都有一些),以防止模型因为最近看到某个类别较多而对该类别产生偏向。因此,我们通常会随机打乱数据。在之前的训练数据(例如螺旋数据)中,我们不需要打乱数据,因为我们是一次性对整个数据集进行训练,而不是分批次训练。但对于这个更大的数据集,我们是以批次进行训练的,因此需要打乱数据,因为目前数据是按每个标签的6,000个样本块顺序排列的。
在打乱数据时,我们需要确保样本数组和目标数组同步打乱,否则标签将不再与样本匹配,导致模型非常混乱(在大多数情况下结果也非常错误)。因此,我们不能简单地分别对它们调用shuffle()方法。有许多方法可以实现这一点,但我们的方法是获取所有的"键"(在这里是样本和目标数组的索引),然后对这些键进行打乱。
在这个例子中,这些键的值范围是从0到59999。
python
keys = np.array(range(X.shape[0]))
print(keys[:10])
python
>>>
array([0 1 2 3 4 5 6 7 8 9])然后,我们就可以对这些密钥进行洗牌:
python
import nnfs
nnfs.init()
np.random.shuffle(keys)
print(keys[:10])
python
>>>
[ 3048 19563 58303 8870 40228 31488 21860 56864 845 25770]现在,这基本上就是新的索引顺序,我们可以通过操作来应用它:
python
X = X[keys]
y = y[keys]这告诉NumPy按照给定的索引返回对应的值,就像我们通常对NumPy数组进行索引一样,但这里我们使用的是一个包含随机顺序索引的变量。然后我们可以检查目标数据的一部分切片:
python
print(y[:15])
python
>>>
[0 3 9 1 6 5 3 9 0 4 8 9 0 6 6]它们似乎被洗过。我们也可以检查个别样本:
python
import matplotlib.pyplot as plt
plt.imshow((X[4].reshape(28, 28))) # Reshape as image is a vector already
plt.show()洗牌之后随机的shirt图片
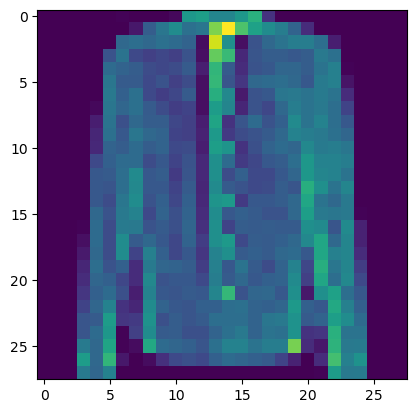
然后,我们就可以在同一索引下检查该类:
python
print(y[4])
python
>>>
6类别6确实是"衬衫",因此这些数据看起来已经正确地打乱了。你可以手动再检查一些数据,以确保数据符合预期。如果模型无法训练或表现异常,你需要仔细检查数据的预处理过程。
批次(Batches)
到目前为止,我们通过将整个数据集作为一个单一的"批次"传递给模型来训练我们的模型。我们在第2章中讨论过为什么一次处理多个样本是更优的,但是否存在一个过大的批次大小呢?我们的数据集足够小,可以一次性传递整个数据集,但真实世界中的数据集通常可能有TB或更多的规模,这对于大多数计算机来说无法作为一个单一批次处理。
批次是数据的一个固定大小的切片。当我们使用批次进行训练时,我们一次以一个数据块或"批次"来迭代数据集,依次执行前向传播、损失计算、反向传播和优化。如果数据已经被打乱,并且每个批次足够大且能在一定程度上代表整个数据集,那么可以合理地假设每个批次的梯度方向是朝向全局最小值的良好近似。如果批次太小,梯度下降的方向可能会在不同批次之间波动过大,导致模型训练耗时较长。
常见的批次大小范围是32到128个样本。如果你的内存不足,可以使用更小的批次;如果想让训练更快,可以使用更大的批次,但通常这个范围是典型的批次大小范围。通过将批次大小从2增加到8,或者从8增加到32,通常可以看到准确率和损失的改善。然而,继续增大批次大小时,关于准确率和损失的提升会逐渐减少。此外,与较小的批次相比,使用大批次进行训练会变得更慢------就像我们之前使用螺旋数据的例子,需要1万轮训练!在神经网络中,很多时候需要针对具体的数据和模型进行大量的试验和调整。
例如,假设我们选择批次大小为128,并选择进行10轮训练。这意味着,在每一轮训练中,我们会遍历数据集,每次拟合128个样本来训练模型。每次训练的批次被称为一个"步骤"。我们可以通过将样本数量除以批次大小来计算步骤的数量:
python
steps = X.shape[0] // BATCH_SIZE我们使用整数除法运算符//(而不是浮点除法运算符/)来返回整数,因为步骤的数量不能包含小数部分。这是我们在每一轮训练中循环执行的迭代次数。如果有一些剩余的样本无法被整除,我们可以通过简单地增加一步来将它们包含进去:
python
if steps * BATCH_SIZE < X.shape[0]:
steps += 1我们可以通过一个简单的例子来说明为什么要添加这个 1:
python
batch_size = 2
X = [1, 2, 3, 4]
print(len(X) // batch_size)
python
>>>
2
python
X = [1, 2, 3, 4, 5]
print(len(X) // batch_size)
python
>>>
2整数除法会向下取整;因此,如果有剩余的样本,我们会加1以形成包含余数的最后一个批次。
以下是使用批次训练模型的代码示例:
python
import nnfs
from nnfs.datasets import spiral_data
nnfs.init()
# Create dataset
X, y = spiral_data(samples=100, classes=3)
EPOCHS = 10 # Train 10 times
BATCH_SIZE = 128 # We take 128 samples at once
# Calculate number of steps
steps = X.shape[0] // BATCH_SIZE
# Dividing rounds down. If there are some remaining data,
# but not a full batch, this won't include it.
# Add 1 to include the remaining samples in 1 more step.
if steps * BATCH_SIZE < X.shape[0]:
steps += 1
for epoch in range(EPOCHS):
for step in range(steps):
batch_X = X[step*BATCH_SIZE:(step+1)*BATCH_SIZE]
batch_y = y[step*BATCH_SIZE:(step+1)*BATCH_SIZE]
# Now we perform forward pass, loss calculation,
# backward pass and update parameters我们加载了数据集,定义了训练轮数(epochs)和批次大小(batch size),然后计算了步骤的数量。接下来,我们有两个循环------一个是遍历训练轮数的外循环,另一个是遍历步骤的内循环。在每一轮的每一步中,我们会选择训练数据的一个切片。现在我们已经知道如何以批次方式训练模型,我们希望了解每一步和每一轮的训练损失和准确率。
到目前为止,我们仅计算了每次拟合的损失,但要记住之前我们是一次性针对整个数据集进行拟合的。现在,我们对批次统计和轮次统计都感兴趣。对于总体损失和准确率,我们希望计算样本级别的平均值。为此,我们将在每轮结束时累积所有批次的损失总和和样本数量,并计算平均值。
我们将在常见的Loss类的calculate方法中添加以下内容:
python
# Add accumulated sum of losses and sample count
self.accumulated_sum += np.sum(sample_losses)
self.accumulated_count += len(sample_losses)(这里不着急,后面会有整体代码展示。在这里,我们只需要懂得是什么意思就好。)
在Loss类中完整实现calculate方法:
python
# Calculates the data and regularization losses
# given model output and ground truth values
def calculate(self, output, y, *, include_regularization=False):
# Calculate sample losses
sample_losses = self.forward(output, y)
# Calculate mean loss
data_loss = np.mean(sample_losses)
# Add accumulated sum of losses and sample count
self.accumulated_sum += np.sum(sample_losses)
self.accumulated_count += len(sample_losses)
# If just data loss - return it
if not include_regularization:
return data_loss
# Return the data and regularization losses
return data_loss, self.regularization_loss() 我们保存了总和和计数,以便可以随时计算平均值。为此,我们将在Loss类中添加一个名为calculate_accumulated的新方法:
python
# Calculates accumulated loss
def calculate_accumulated(self, *, include_regularization=False):
# Calculate mean loss
data_loss = self.accumulated_sum / self.accumulated_count
# If just data loss - return it
if not include_regularization:
return data_loss
# Return the data and regularization losses
return data_loss, self.regularization_loss()此方法还可以在include_regularization设置为True时返回正则化损失。正则化损失不需要累积,因为它是根据当前的层参数状态计算的,在调用时直接生成。我们将在训练过程中使用这一功能,但在评估和预测时不会使用;我们稍后会对此进行更详细的讨论。
最后,为了在新一轮训练中重置总和和计数值,我们将添加最后一个方法:
python
# Reset variables for accumulated loss
def new_pass(self):
self.accumulated_sum = 0
self.accumulated_count = 0完整实现我们的通用Loss类:
python
# Common loss class
class Loss:
# Regularization loss calculation
def regularization_loss(self):
# 0 by default
regularization_loss = 0
# Calculate regularization loss
# iterate all trainable layers
for layer in self.trainable_layers:
# L1 regularization - weights
# calculate only when factor greater than 0
if layer.weight_regularizer_l1 > 0:
regularization_loss += layer.weight_regularizer_l1 * np.sum(np.abs(layer.weights))
# L2 regularization - weights
if layer.weight_regularizer_l2 > 0:
regularization_loss += layer.weight_regularizer_l2 * np.sum(layer.weights * layer.weights)
# L1 regularization - biases
# calculate only when factor greater than 0
if layer.bias_regularizer_l1 > 0:
regularization_loss += layer.bias_regularizer_l1 * np.sum(np.abs(layer.biases))
# L2 regularization - biases
if layer.bias_regularizer_l2 > 0:
regularization_loss += layer.bias_regularizer_l2 * np.sum(layer.biases * layer.biases)
return regularization_loss
# Set/remember trainable layers
def remember_trainable_layers(self, trainable_layers):
self.trainable_layers = trainable_layers
# Calculates the data and regularization losses
# given model output and ground truth values
def calculate(self, output, y, *, include_regularization=False):
# Calculate sample losses
sample_losses = self.forward(output, y)
# Calculate mean loss
data_loss = np.mean(sample_losses)
# Add accumulated sum of losses and sample count
self.accumulated_sum += np.sum(sample_losses)
self.accumulated_count += len(sample_losses)
# If just data loss - return it
if not include_regularization:
return data_loss
# Return the data and regularization losses
return data_loss, self.regularization_loss()
# Calculates accumulated loss
def calculate_accumulated(self, *, include_regularization=False):
# Calculate mean loss
data_loss = self.accumulated_sum / self.accumulated_count
# If just data loss - return it
if not include_regularization:
return data_loss
# Return the data and regularization losses
return data_loss, self.regularization_loss()
# Reset variables for accumulated loss
def new_pass(self):
self.accumulated_sum = 0
self.accumulated_count = 0现在我们需要为Accuracy类实现相同的功能:
python
# Common accuracy class
class Accuracy:
# Calculates an accuracy
# given predictions and ground truth values
def calculate(self, predictions, y):
# Get comparison results
comparisons = self.compare(predictions, y)
# Calculate an accuracy
accuracy = np.mean(comparisons)
# Add accumulated sum of matching values and sample count
self.accumulated_sum += np.sum(comparisons)
self.accumulated_count += len(comparisons)
# Return accuracy
return accuracy
# Calculates accumulated accuracy
def calculate_accumulated(self):
# Calculate an accuracy
accuracy = self.accumulated_sum / self.accumulated_count
# Return the data and regularization losses
return accuracy
# Reset variables for accumulated accuracy
def new_pass(self):
self.accumulated_sum = 0
self.accumulated_count = 0在这里,我们在calculate方法中添加了设置accumulated_sum和accumulated_count属性的功能,用于计算每轮训练的准确率;添加了一个新的calculate_accumulated方法来返回累积的准确率;最后,添加了一个new_pass方法,用于在每轮训练开始时重置accumulated_sum和accumulated_count的值。
现在,我们将修改Model类的train方法。首先,我们将添加一个名为batch_size的新参数(这里不着急,后面会有整体代码展示。在这里,我们只需要懂得是什么意思就好。):
python
def train(self, X, y, *, epochs=1, batch_size=None, print_every=1, validation_data=None):我们将默认将此参数设置为None,这意味着使用整个数据集作为一个批次。在这种情况下,每轮训练只需要一步,这一步包括将所有数据一次性传递通过网络。
python
# Default value if batch size is not set
train_steps = 1
# If there is validation data passed,
# set default number of steps for validation as well
if validation_data is not None:
validation_steps = 1
# For better readability
X_val, y_val = validation_data如前所述,大多数"现实生活"中的数据集需要的批次大小小于所有样本的数量。我们将使用之前描述的方法来处理这一点:对样本总数进行整数除法得到批次数量,并最终加1以包括未组成完整批次的剩余样本(我们将对训练数据和验证数据都这样处理):
python
# Calculate number of steps
if batch_size is not None:
train_steps = len(X) // batch_size
# Dividing rounds down. If there are some remaining
# data, but not a full batch, this won't include it
# Add 1 to include this not full batch
if train_steps * batch_size < len(X):
train_steps += 1
if validation_data is not None:
validation_steps = len(X_val) // batch_size
# Dividing rounds down. If there are some remaining
# data, but nor full batch, this won't include it
# Add 1 to include this not full batch
if validation_steps * batch_size < len(X_val):
validation_steps += 1接下来,从顶部开始,我们将修改遍历训练轮数的循环,打印轮数编号,并重置累积的轮次损失和准确率值。然后,在其中添加一个新循环,用于遍历当前轮次中的各个步骤。
python
# Main training loop
for epoch in range(1, epochs+1):
# Print epoch number
print(f'epoch: {epoch}')
# Reset accumulated values in loss and accuracy objects
self.loss.new_pass()
self.accuracy.new_pass()
# Iterate over steps
for step in range(train_steps):在每一步中,我们需要获取用于训练的数据批次------如果batch_size参数仍然是默认值None,则使用整个数据集;否则,获取大小为batch_size的切片数据:
python
# If batch size is not set -
# train using one step and full dataset
if batch_size is None:
batch_X = X
batch_y = y
# Otherwise slice a batch
else:
batch_X = X[step*batch_size:(step+1)*batch_size]
batch_y = y[step*batch_size:(step+1)*batch_size]对于每个批次,我们进行拟合并打印信息,类似于之前按轮次拟合的方式。不同之处在于现在使用的是batch_X而不是X,以及batch_y而不是y。另一个变化是用于打印摘要的if语句,现在是基于步骤而不是轮次:
python
# Perform the forward pass
output = self.forward(batch_X, training=True)
# Calculate loss
data_loss, regularization_loss = self.loss.calculate(output, batch_y,
include_regularization=True)
loss = data_loss + regularization_loss
# Get predictions and calculate an accuracy
predictions = self.output_layer_activation.predictions(output)
accuracy = self.accuracy.calculate(predictions, batch_y)
# Perform backward pass
self.backward(output, batch_y)
# Optimize (update parameters)
self.optimizer.pre_update_params()
for layer in self.trainable_layers:
self.optimizer.update_params(layer)
self.optimizer.post_update_params()
# Print a summary
if not step % print_every or step == train_steps - 1:
print(f'step: {step}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {self.optimizer.current_learning_rate}')然后我们需要打印每轮的准确率和损失等信息:
python
# Get and print epoch loss and accuracy
epoch_data_loss, epoch_regularization_loss = self.loss.calculate_accumulated(include_regularization=True)
epoch_loss = epoch_data_loss + epoch_regularization_loss
epoch_accuracy = self.accuracy.calculate_accumulated()
print(f'training, ' +
f'acc: {epoch_accuracy:.3f}, ' +
f'loss: {epoch_loss:.3f} (' +
f'data_loss: {epoch_data_loss:.3f}, ' +
f'reg_loss: {epoch_regularization_loss:.3f}), ' +
f'lr: {self.optimizer.current_learning_rate}')如果设置了批次大小,验证数据很可能大于这个批次大小,因此我们也需要为验证数据添加批处理功能:
python
# If there is the validation data
if validation_data is not None:
# Reset accumulated values in loss
# and accuracy objects
self.loss.new_pass()
self.accuracy.new_pass()
# Iterate over steps
for step in range(validation_steps):
# If batch size is not set -
# train using one step and full dataset
if batch_size is None:
batch_X = X_val
batch_y = y_val
# Otherwise slice a batch
else:
batch_X = X_val[step*batch_size:(step+1)*batch_size]
batch_y = y_val[step*batch_size:(step+1)*batch_size]
# Perform the forward pass
output = self.forward(batch_X, training=False)
# Calculate the loss
self.loss.calculate(output, batch_y)
# Get predictions and calculate an accuracy
predictions = self.output_layer_activation.predictions(output)
self.accuracy.calculate(predictions, batch_y)
# Get and print validation loss and accuracy
validation_loss = self.loss.calculate_accumulated()
validation_accuracy = self.accuracy.calculate_accumulated()
print(f'validation, ' +
f'acc: {validation_accuracy:.3f}, ' +
f'loss: {validation_loss:.3f}')与当前代码相比,我们添加了对损失和准确率对象的new_pass方法的调用,该方法会重置训练步骤中累积的值。接着,我们引入了批次处理(一个遍历步骤的循环),并移除了对损失计算结果的捕获(在验证过程中,我们只关注最终的整体损失,而不是每个批次的损失)。最后的步骤是处理整体验证损失,并将X_val替换为batch_X,将y_val替换为batch_y,以匹配对训练代码所做的更改。
这构成了我们Model类完整的train方法:
python
# Train the model
# def train(self, X, y, *, epochs=1, print_every=1, validation_data=None):
def train(self, X, y, *, epochs=1, batch_size=None, print_every=1, validation_data=None):
# Initialize accuracy object
self.accuracy.init(y)
# Default value if batch size is not being set
train_steps = 1
# If there is validation data passed,
# set default number of steps for validation as well
if validation_data is not None:
validation_steps = 1
# For better readability
X_val, y_val = validation_data
# Calculate number of steps
if batch_size is not None:
train_steps = len(X) // batch_size
# Dividing rounds down. If there are some remaining
# data, but not a full batch, this won't include it
# Add `1` to include this not full batch
if train_steps * batch_size < len(X):
train_steps += 1
if validation_data is not None:
validation_steps = len(X_val) // batch_size
# Dividing rounds down. If there are some remaining
# data, but nor full batch, this won't include it
# Add `1` to include this not full batch
if validation_steps * batch_size < len(X_val):
validation_steps += 1
# Main training loop
for epoch in range(1, epochs+1):
# Print epoch number
print(f'epoch: {epoch}')
# Reset accumulated values in loss and accuracy objects
self.loss.new_pass()
self.accuracy.new_pass()
# Iterate over steps
for step in range(train_steps):
# If batch size is not set -
# train using one step and full dataset
if batch_size is None:
batch_X = X
batch_y = y
# Otherwise slice a batch
else:
batch_X = X[step*batch_size:(step+1)*batch_size]
batch_y = y[step*batch_size:(step+1)*batch_size]
# Perform the forward pass
output = self.forward(batch_X, training=True)
# Calculate loss
data_loss, regularization_loss = self.loss.calculate(output, batch_y, include_regularization=True)
loss = data_loss + regularization_loss
# Get predictions and calculate an accuracy
predictions = self.output_layer_activation.predictions(output)
accuracy = self.accuracy.calculate(predictions, batch_y)
# Perform backward pass
self.backward(output, batch_y)
# Optimize (update parameters)
self.optimizer.pre_update_params()
for layer in self.trainable_layers:
self.optimizer.update_params(layer)
self.optimizer.post_update_params()
# Print a summary
if not step % print_every or step == train_steps - 1:
print(f'step: {step}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {self.optimizer.current_learning_rate}')
# Get and print epoch loss and accuracy
epoch_data_loss, epoch_regularization_loss = self.loss.calculate_accumulated(include_regularization=True)
epoch_loss = epoch_data_loss + epoch_regularization_loss
epoch_accuracy = self.accuracy.calculate_accumulated()
print(f'training, ' +
f'acc: {epoch_accuracy:.3f}, ' +
f'loss: {epoch_loss:.3f} (' +
f'data_loss: {epoch_data_loss:.3f}, ' +
f'reg_loss: {epoch_regularization_loss:.3f}), ' +
f'lr: {self.optimizer.current_learning_rate}')
# If there is the validation data
if validation_data is not None:
# Reset accumulated values in loss
# and accuracy objects
self.loss.new_pass()
self.accuracy.new_pass()
# Iterate over steps
for step in range(validation_steps):
# If batch size is not set -
# train using one step and full dataset
if batch_size is None:
batch_X = X_val
batch_y = y_val
# Otherwise slice a batch
else:
batch_X = X_val[step*batch_size:(step+1)*batch_size]
batch_y = y_val[step*batch_size:(step+1)*batch_size]
# Perform the forward pass
output = self.forward(batch_X, training=False)
# Calculate the loss
self.loss.calculate(output, batch_y)
# Get predictions and calculate an accuracy
predictions = self.output_layer_activation.predictions(output)
self.accuracy.calculate(predictions, batch_y)
# Get and print validation loss and accuracy
validation_loss = self.loss.calculate_accumulated()
validation_accuracy = self.accuracy.calculate_accumulated()
# Print a summary
print(f'validation, ' +
f'acc: {validation_accuracy:.3f}, ' +
f'loss: {validation_loss:.3f}')训练(Training)
此时,我们已经准备好使用批次和新数据集进行训练。提醒一下,我们通过以下方式创建数据:
python
# Create dataset
X, y, X_test, y_test = create_data_mnist('fashion_mnist_images')然后洗牌(shuffle):
python
# Shuffle the training dataset
keys = np.array(range(X.shape[0]))
np.random.shuffle(keys)
X = X[keys]
y = y[keys]然后平移样本,缩放至 -1 至 1 的范围:
python
# Scale and reshape samples
X = (X.reshape(X.shape[0], -1).astype(np.float32) - 127.5) / 127.5
X_test = (X_test.reshape(X_test.shape[0], -1).astype(np.float32) - 127.5) / 127.5然后构建我们的模型,包括两个使用ReLU激活的隐藏层,一个使用softmax激活的输出层(因为我们正在构建一个分类模型),交叉熵损失函数,Adam优化器,以及分类准确率:
python
# Instantiate the model
model = Model()
# Add layers
model.add(Layer_Dense(X.shape[1], 64))
model.add(Activation_ReLU())
model.add(Layer_Dense(64, 64))
model.add(Activation_ReLU())
model.add(Layer_Dense(64, 10))
model.add(Activation_Softmax())设置损耗、优化器和精度对象:
python
# Set loss, optimizer and accuracy objects
model.set(
loss=Loss_CategoricalCrossentropy(),
optimizer=Optimizer_Adam(decay=5e-5),
accuracy=Accuracy_Categorical()
)最后,我们最后确定并进行培训!
python
# Finalize the model
model.finalize()
# Train the model
model.train(X, y, validation_data=(X_test, y_test), epochs=5, batch_size=128, print_every=100)
python
>>>
epoch: 1
step: 0, acc: 0.078, loss: 2.473 (data_loss: 2.473, reg_loss: 0.000), lr: 0.001
step: 100, acc: 0.766, loss: 0.527 (data_loss: 0.527, reg_loss: 0.000), lr: 0.0009950248756218907
step: 200, acc: 0.852, loss: 0.417 (data_loss: 0.417, reg_loss: 0.000), lr: 0.0009900990099009901
step: 300, acc: 0.797, loss: 0.511 (data_loss: 0.511, reg_loss: 0.000), lr: 0.0009852216748768474
step: 400, acc: 0.828, loss: 0.434 (data_loss: 0.434, reg_loss: 0.000), lr: 0.000980392156862745
step: 468, acc: 0.865, loss: 0.305 (data_loss: 0.305, reg_loss: 0.000), lr: 0.0009771350400625367
training, acc: 0.797, loss: 0.568 (data_loss: 0.568, reg_loss: 0.000), lr: 0.0009771350400625367
validation, acc: 0.843, loss: 0.445
epoch: 2
step: 0, acc: 0.859, loss: 0.377 (data_loss: 0.377, reg_loss: 0.000), lr: 0.0009770873027505008
step: 100, acc: 0.820, loss: 0.434 (data_loss: 0.434, reg_loss: 0.000), lr: 0.000972337012008362
step: 200, acc: 0.867, loss: 0.318 (data_loss: 0.318, reg_loss: 0.000), lr: 0.0009676326866321544
step: 300, acc: 0.867, loss: 0.430 (data_loss: 0.430, reg_loss: 0.000), lr: 0.0009629736626703259
step: 400, acc: 0.836, loss: 0.398 (data_loss: 0.398, reg_loss: 0.000), lr: 0.0009583592888974076
step: 468, acc: 0.906, loss: 0.248 (data_loss: 0.248, reg_loss: 0.000), lr: 0.0009552466924583273
training, acc: 0.857, loss: 0.397 (data_loss: 0.397, reg_loss: 0.000), lr: 0.0009552466924583273
validation, acc: 0.856, loss: 0.400
epoch: 3
step: 0, acc: 0.883, loss: 0.317 (data_loss: 0.317, reg_loss: 0.000), lr: 0.0009552010698251983
step: 100, acc: 0.852, loss: 0.355 (data_loss: 0.355, reg_loss: 0.000), lr: 0.0009506607091928891
step: 200, acc: 0.883, loss: 0.288 (data_loss: 0.288, reg_loss: 0.000), lr: 0.0009461633077869241
step: 300, acc: 0.898, loss: 0.391 (data_loss: 0.391, reg_loss: 0.000), lr: 0.0009417082587814295
step: 400, acc: 0.859, loss: 0.367 (data_loss: 0.367, reg_loss: 0.000), lr: 0.0009372949667260287
step: 468, acc: 0.906, loss: 0.219 (data_loss: 0.219, reg_loss: 0.000), lr: 0.000934317481080071
training, acc: 0.871, loss: 0.355 (data_loss: 0.355, reg_loss: 0.000), lr: 0.000934317481080071
validation, acc: 0.863, loss: 0.380
epoch: 4
step: 0, acc: 0.867, loss: 0.294 (data_loss: 0.294, reg_loss: 0.000), lr: 0.0009342738356612324
step: 100, acc: 0.852, loss: 0.323 (data_loss: 0.323, reg_loss: 0.000), lr: 0.0009299297903008323
step: 200, acc: 0.883, loss: 0.271 (data_loss: 0.271, reg_loss: 0.000), lr: 0.0009256259545517657
step: 300, acc: 0.914, loss: 0.369 (data_loss: 0.369, reg_loss: 0.000), lr: 0.0009213617727000506
step: 400, acc: 0.875, loss: 0.349 (data_loss: 0.349, reg_loss: 0.000), lr: 0.0009171366992250195
step: 468, acc: 0.906, loss: 0.197 (data_loss: 0.197, reg_loss: 0.000), lr: 0.0009142857142857143
training, acc: 0.878, loss: 0.331 (data_loss: 0.331, reg_loss: 0.000), lr: 0.0009142857142857143
validation, acc: 0.867, loss: 0.368
epoch: 5
step: 0, acc: 0.867, loss: 0.278 (data_loss: 0.278, reg_loss: 0.000), lr: 0.0009142439202779302
step: 100, acc: 0.867, loss: 0.297 (data_loss: 0.297, reg_loss: 0.000), lr: 0.0009100837277029487
step: 200, acc: 0.891, loss: 0.258 (data_loss: 0.258, reg_loss: 0.000), lr: 0.0009059612248595759
step: 300, acc: 0.891, loss: 0.340 (data_loss: 0.340, reg_loss: 0.000), lr: 0.0009018759018759019
step: 400, acc: 0.875, loss: 0.335 (data_loss: 0.335, reg_loss: 0.000), lr: 0.0008978272580355541
step: 468, acc: 0.917, loss: 0.186 (data_loss: 0.186, reg_loss: 0.000), lr: 0.0008950948800572861
training, acc: 0.885, loss: 0.312 (data_loss: 0.312, reg_loss: 0.000), lr: 0.0008950948800572861
validation, acc: 0.871, loss: 0.359模型成功训练并取得了相当不错的准确率。这是在一个新的、真实的、更具挑战性的数据集上完成的,并且仅用了5个训练轮次,而不是之前螺旋数据的10000轮。同时,训练速度也比我们之前对螺旋数据一次性拟合整个数据集时更快。
到目前为止,我们仅提到打乱训练数据的重要性,以及如果尝试在未打乱的数据上进行训练可能会发生什么。现在是一个很好的时机来示例当我们不打乱数据时会发生什么。我们可以将打乱数据的代码注释掉:
python
# # Shuffle the training dataset
# keys = np.array(range(X.shape[0]))
# np.random.shuffle(keys)
# X = X[keys]
# y = y[keys]再次运行,我们可以看到:
python
>>>
epoch: 1
step: 0, acc: 0.000, loss: 2.320 (data_loss: 2.320, reg_loss: 0.000), lr: 0.001
step: 100, acc: 0.000, loss: 3.763 (data_loss: 3.763, reg_loss: 0.000), lr: 0.0009950248756218907
step: 200, acc: 0.000, loss: 2.677 (data_loss: 2.677, reg_loss: 0.000), lr: 0.0009900990099009901
step: 300, acc: 1.000, loss: 0.421 (data_loss: 0.421, reg_loss: 0.000), lr: 0.0009852216748768474
step: 400, acc: 1.000, loss: 0.023 (data_loss: 0.023, reg_loss: 0.000), lr: 0.000980392156862745
step: 468, acc: 1.000, loss: 0.004 (data_loss: 0.004, reg_loss: 0.000), lr: 0.0009771350400625367
training, acc: 0.657, loss: 1.930 (data_loss: 1.930, reg_loss: 0.000), lr: 0.0009771350400625367
validation, acc: 0.109, loss: 5.800
epoch: 2
step: 0, acc: 0.000, loss: 3.527 (data_loss: 3.527, reg_loss: 0.000), lr: 0.0009770873027505008
step: 100, acc: 0.000, loss: 3.722 (data_loss: 3.722, reg_loss: 0.000), lr: 0.000972337012008362
step: 200, acc: 0.531, loss: 1.189 (data_loss: 1.189, reg_loss: 0.000), lr: 0.0009676326866321544
step: 300, acc: 0.961, loss: 0.504 (data_loss: 0.504, reg_loss: 0.000), lr: 0.0009629736626703259
step: 400, acc: 0.984, loss: 0.063 (data_loss: 0.063, reg_loss: 0.000), lr: 0.0009583592888974076
step: 468, acc: 1.000, loss: 0.004 (data_loss: 0.004, reg_loss: 0.000), lr: 0.0009552466924583273
training, acc: 0.746, loss: 1.066 (data_loss: 1.066, reg_loss: 0.000), lr: 0.0009552466924583273
validation, acc: 0.110, loss: 5.365
epoch: 3
step: 0, acc: 0.000, loss: 4.172 (data_loss: 4.172, reg_loss: 0.000), lr: 0.0009552010698251983
step: 100, acc: 0.336, loss: 1.288 (data_loss: 1.288, reg_loss: 0.000), lr: 0.0009506607091928891
step: 200, acc: 0.680, loss: 1.366 (data_loss: 1.366, reg_loss: 0.000), lr: 0.0009461633077869241
step: 300, acc: 1.000, loss: 0.017 (data_loss: 0.017, reg_loss: 0.000), lr: 0.0009417082587814295
step: 400, acc: 0.984, loss: 0.128 (data_loss: 0.128, reg_loss: 0.000), lr: 0.0009372949667260287
step: 468, acc: 1.000, loss: 0.001 (data_loss: 0.001, reg_loss: 0.000), lr: 0.000934317481080071
training, acc: 0.782, loss: 0.838 (data_loss: 0.838, reg_loss: 0.000), lr: 0.000934317481080071
validation, acc: 0.209, loss: 4.189
epoch: 4
step: 0, acc: 0.000, loss: 2.829 (data_loss: 2.829, reg_loss: 0.000), lr: 0.0009342738356612324
step: 100, acc: 0.031, loss: 2.136 (data_loss: 2.136, reg_loss: 0.000), lr: 0.0009299297903008323
step: 200, acc: 0.609, loss: 1.109 (data_loss: 1.109, reg_loss: 0.000), lr: 0.0009256259545517657
step: 300, acc: 0.984, loss: 0.097 (data_loss: 0.097, reg_loss: 0.000), lr: 0.0009213617727000506
step: 400, acc: 0.984, loss: 0.034 (data_loss: 0.034, reg_loss: 0.000), lr: 0.0009171366992250195
step: 468, acc: 1.000, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.0009142857142857143
training, acc: 0.813, loss: 0.719 (data_loss: 0.719, reg_loss: 0.000), lr: 0.0009142857142857143
validation, acc: 0.164, loss: 7.111
epoch: 5
step: 0, acc: 0.000, loss: 5.931 (data_loss: 5.931, reg_loss: 0.000), lr: 0.0009142439202779302
step: 100, acc: 0.781, loss: 0.784 (data_loss: 0.784, reg_loss: 0.000), lr: 0.0009100837277029487
step: 200, acc: 0.750, loss: 0.808 (data_loss: 0.808, reg_loss: 0.000), lr: 0.0009059612248595759
step: 300, acc: 0.984, loss: 0.133 (data_loss: 0.133, reg_loss: 0.000), lr: 0.0009018759018759019
step: 400, acc: 0.961, loss: 0.091 (data_loss: 0.091, reg_loss: 0.000), lr: 0.0008978272580355541
step: 468, acc: 1.000, loss: 0.002 (data_loss: 0.002, reg_loss: 0.000), lr: 0.0008950948800572861
training, acc: 0.860, loss: 0.544 (data_loss: 0.544, reg_loss: 0.000), lr: 0.0008950948800572861
validation, acc: 0.224, loss: 4.844正如我们所见,这种方式效果非常差。我们可以观察到,模型在训练过程中接近完美的准确率1,但轮次准确率仍然很差,验证准确率证明模型并未真正学习。训练准确率快速升高,因为模型学会了只预测一个标签(因为它反复只看到那个标签)。当训练数据中的标签改变时,模型很快学会了只预测新的标签,因为它在每个批次中看到的全是那个标签。这一过程在一个轮次结束后重复,在所有轮次中循环。
轮次准确率较低,因为模型在切换标签后需要一段时间来学习新标签,在此期间准确率较低。验证准确率是在特定轮次的训练结束后计算的,正如我们所记得的,模型只学会预测一个标签。在验证过程中,模型预测的标签是它最后看到的标签------准确率接近 1 / 10 1/10 1/10,因为我们的训练数据集包含10个类别。
重新启用数据打乱功能,然后可以调整模型,看看是否能进一步改进结果。以下是一个示例,使用更大的模型、更高的学习率衰减,以及两倍的训练轮次:
python
# Add layers
model.add(Layer_Dense(X.shape[1], 128))
model.add(Activation_ReLU())
model.add(Layer_Dense(128, 128))
model.add(Activation_ReLU())
model.add(Layer_Dense(128, 10))
model.add(Activation_Softmax())
# Set loss, optimizer and accuracy objects
model.set(
loss=Loss_CategoricalCrossentropy(),
optimizer=Optimizer_Adam(decay=1e-3),
accuracy=Accuracy_Categorical()
)
# Finalize the model
model.finalize()
# Train the model
model.train(X, y, validation_data=(X_test, y_test), epochs=10, batch_size=128, print_every=100)
python
>>>
epoch: 1
step: 0, acc: 0.031, loss: 3.608 (data_loss: 3.608, reg_loss: 0.000), lr: 0.001
step: 100, acc: 0.773, loss: 0.542 (data_loss: 0.542, reg_loss: 0.000), lr: 0.0009090909090909091
step: 200, acc: 0.883, loss: 0.325 (data_loss: 0.325, reg_loss: 0.000), lr: 0.0008333333333333334
step: 300, acc: 0.875, loss: 0.439 (data_loss: 0.439, reg_loss: 0.000), lr: 0.0007692307692307692
step: 400, acc: 0.836, loss: 0.422 (data_loss: 0.422, reg_loss: 0.000), lr: 0.0007142857142857143
step: 468, acc: 0.875, loss: 0.291 (data_loss: 0.291, reg_loss: 0.000), lr: 0.000681198910081744
training, acc: 0.813, loss: 0.519 (data_loss: 0.519, reg_loss: 0.000), lr: 0.000681198910081744
validation, acc: 0.843, loss: 0.429
epoch: 2
step: 0, acc: 0.836, loss: 0.373 (data_loss: 0.373, reg_loss: 0.000), lr: 0.0006807351940095304
step: 100, acc: 0.812, loss: 0.387 (data_loss: 0.387, reg_loss: 0.000), lr: 0.0006373486297004461
step: 200, acc: 0.867, loss: 0.285 (data_loss: 0.285, reg_loss: 0.000), lr: 0.0005991611743559018
step: 300, acc: 0.891, loss: 0.384 (data_loss: 0.384, reg_loss: 0.000), lr: 0.0005652911249293386
step: 400, acc: 0.844, loss: 0.381 (data_loss: 0.381, reg_loss: 0.000), lr: 0.0005350454788657037
step: 468, acc: 0.896, loss: 0.214 (data_loss: 0.214, reg_loss: 0.000), lr: 0.0005162622612287042
training, acc: 0.866, loss: 0.370 (data_loss: 0.370, reg_loss: 0.000), lr: 0.0005162622612287042
validation, acc: 0.859, loss: 0.384
epoch: 3
step: 0, acc: 0.844, loss: 0.330 (data_loss: 0.330, reg_loss: 0.000), lr: 0.0005159958720330237
step: 100, acc: 0.852, loss: 0.328 (data_loss: 0.328, reg_loss: 0.000), lr: 0.0004906771344455348
step: 200, acc: 0.898, loss: 0.251 (data_loss: 0.251, reg_loss: 0.000), lr: 0.0004677268475210477
step: 300, acc: 0.883, loss: 0.345 (data_loss: 0.345, reg_loss: 0.000), lr: 0.00044682752457551384
step: 400, acc: 0.859, loss: 0.352 (data_loss: 0.352, reg_loss: 0.000), lr: 0.00042771599657827206
step: 468, acc: 0.917, loss: 0.185 (data_loss: 0.185, reg_loss: 0.000), lr: 0.0004156275976724854
training, acc: 0.880, loss: 0.329 (data_loss: 0.329, reg_loss: 0.000), lr: 0.0004156275976724854
validation, acc: 0.866, loss: 0.364
epoch: 4
step: 0, acc: 0.852, loss: 0.302 (data_loss: 0.302, reg_loss: 0.000), lr: 0.0004154549231408392
step: 100, acc: 0.875, loss: 0.278 (data_loss: 0.278, reg_loss: 0.000), lr: 0.00039888312724371757
step: 200, acc: 0.930, loss: 0.232 (data_loss: 0.232, reg_loss: 0.000), lr: 0.0003835826620636747
step: 300, acc: 0.898, loss: 0.310 (data_loss: 0.310, reg_loss: 0.000), lr: 0.0003694126339120798
step: 400, acc: 0.867, loss: 0.336 (data_loss: 0.336, reg_loss: 0.000), lr: 0.0003562522265764161
step: 468, acc: 0.917, loss: 0.177 (data_loss: 0.177, reg_loss: 0.000), lr: 0.00034782608695652176
training, acc: 0.890, loss: 0.304 (data_loss: 0.304, reg_loss: 0.000), lr: 0.00034782608695652176
validation, acc: 0.872, loss: 0.352
epoch: 5
step: 0, acc: 0.883, loss: 0.274 (data_loss: 0.274, reg_loss: 0.000), lr: 0.0003477051460361613
step: 100, acc: 0.898, loss: 0.256 (data_loss: 0.256, reg_loss: 0.000), lr: 0.00033602150537634406
step: 200, acc: 0.922, loss: 0.220 (data_loss: 0.220, reg_loss: 0.000), lr: 0.00032509752925877764
step: 300, acc: 0.914, loss: 0.283 (data_loss: 0.283, reg_loss: 0.000), lr: 0.00031486146095717883
step: 400, acc: 0.867, loss: 0.329 (data_loss: 0.329, reg_loss: 0.000), lr: 0.00030525030525030525
step: 468, acc: 0.917, loss: 0.171 (data_loss: 0.171, reg_loss: 0.000), lr: 0.0002990430622009569
training, acc: 0.896, loss: 0.287 (data_loss: 0.287, reg_loss: 0.000), lr: 0.0002990430622009569
validation, acc: 0.874, loss: 0.347
epoch: 6
step: 0, acc: 0.891, loss: 0.254 (data_loss: 0.254, reg_loss: 0.000), lr: 0.0002989536621823617
step: 100, acc: 0.914, loss: 0.241 (data_loss: 0.241, reg_loss: 0.000), lr: 0.00029027576197387516
step: 200, acc: 0.914, loss: 0.209 (data_loss: 0.209, reg_loss: 0.000), lr: 0.0002820874471086037
step: 300, acc: 0.922, loss: 0.267 (data_loss: 0.267, reg_loss: 0.000), lr: 0.00027434842249657066
step: 400, acc: 0.883, loss: 0.321 (data_loss: 0.321, reg_loss: 0.000), lr: 0.000267022696929239
step: 468, acc: 0.927, loss: 0.163 (data_loss: 0.163, reg_loss: 0.000), lr: 0.00026226068712300026
training, acc: 0.901, loss: 0.273 (data_loss: 0.273, reg_loss: 0.000), lr: 0.00026226068712300026
validation, acc: 0.877, loss: 0.343
epoch: 7
step: 0, acc: 0.898, loss: 0.237 (data_loss: 0.237, reg_loss: 0.000), lr: 0.00026219192448872575
step: 100, acc: 0.922, loss: 0.225 (data_loss: 0.225, reg_loss: 0.000), lr: 0.00025549310168625444
step: 200, acc: 0.930, loss: 0.201 (data_loss: 0.201, reg_loss: 0.000), lr: 0.00024912805181863477
step: 300, acc: 0.922, loss: 0.259 (data_loss: 0.259, reg_loss: 0.000), lr: 0.0002430724355858046
step: 400, acc: 0.883, loss: 0.311 (data_loss: 0.311, reg_loss: 0.000), lr: 0.00023730422401518745
step: 468, acc: 0.927, loss: 0.159 (data_loss: 0.159, reg_loss: 0.000), lr: 0.00023353573096683791
training, acc: 0.906, loss: 0.262 (data_loss: 0.262, reg_loss: 0.000), lr: 0.00023353573096683791
validation, acc: 0.878, loss: 0.340
epoch: 8
step: 0, acc: 0.906, loss: 0.224 (data_loss: 0.224, reg_loss: 0.000), lr: 0.00023348120476301658
step: 100, acc: 0.906, loss: 0.214 (data_loss: 0.214, reg_loss: 0.000), lr: 0.00022815423226100847
step: 200, acc: 0.930, loss: 0.191 (data_loss: 0.191, reg_loss: 0.000), lr: 0.0002230649118893598
step: 300, acc: 0.922, loss: 0.253 (data_loss: 0.253, reg_loss: 0.000), lr: 0.00021819768710451667
step: 400, acc: 0.898, loss: 0.307 (data_loss: 0.307, reg_loss: 0.000), lr: 0.00021353833013025838
step: 468, acc: 0.927, loss: 0.156 (data_loss: 0.156, reg_loss: 0.000), lr: 0.00021048200378867611
training, acc: 0.909, loss: 0.252 (data_loss: 0.252, reg_loss: 0.000), lr: 0.00021048200378867611
validation, acc: 0.878, loss: 0.336
epoch: 9
step: 0, acc: 0.906, loss: 0.209 (data_loss: 0.209, reg_loss: 0.000), lr: 0.0002104377104377104
step: 100, acc: 0.922, loss: 0.202 (data_loss: 0.202, reg_loss: 0.000), lr: 0.0002061005770816158
step: 200, acc: 0.922, loss: 0.181 (data_loss: 0.181, reg_loss: 0.000), lr: 0.00020193861066235866
step: 300, acc: 0.922, loss: 0.250 (data_loss: 0.250, reg_loss: 0.000), lr: 0.0001979414093428345
step: 400, acc: 0.898, loss: 0.303 (data_loss: 0.303, reg_loss: 0.000), lr: 0.0001940993788819876
step: 468, acc: 0.938, loss: 0.151 (data_loss: 0.151, reg_loss: 0.000), lr: 0.00019157088122605365
training, acc: 0.912, loss: 0.244 (data_loss: 0.244, reg_loss: 0.000), lr: 0.00019157088122605365
validation, acc: 0.881, loss: 0.335
epoch: 10
step: 0, acc: 0.906, loss: 0.198 (data_loss: 0.198, reg_loss: 0.000), lr: 0.0001915341888527102
step: 100, acc: 0.930, loss: 0.193 (data_loss: 0.193, reg_loss: 0.000), lr: 0.00018793459875963167
step: 200, acc: 0.922, loss: 0.175 (data_loss: 0.175, reg_loss: 0.000), lr: 0.00018446781036709093
step: 300, acc: 0.922, loss: 0.245 (data_loss: 0.245, reg_loss: 0.000), lr: 0.00018112660749864155
step: 400, acc: 0.898, loss: 0.303 (data_loss: 0.303, reg_loss: 0.000), lr: 0.00017790428749332856
step: 468, acc: 0.938, loss: 0.144 (data_loss: 0.144, reg_loss: 0.000), lr: 0.00017577781683951485
training, acc: 0.915, loss: 0.237 (data_loss: 0.237, reg_loss: 0.000), lr: 0.00017577781683951485
validation, acc: 0.881, loss: 0.334通过简单地增加模型规模、衰减和训练轮次,我们提高了准确率并降低了损失。
到目前为止的全部代码:
python
import numpy as np
import cv2
import os
# Loads a MNIST dataset
def load_mnist_dataset(dataset, path):
# Scan all the directories and create a list of labels
labels = os.listdir(os.path.join(path, dataset))
# Create lists for samples and labels
X = []
y = []
# For each label folder
for label in labels:
# And for each image in given folder
for file in os.listdir(os.path.join(path, dataset, label)):
# Read the image
image = cv2.imread(os.path.join(path, dataset, label, file), cv2.IMREAD_UNCHANGED)
# And append it and a label to the lists
X.append(image)
y.append(label)
# Convert the data to proper numpy arrays and return
return np.array(X), np.array(y).astype('uint8')
# MNIST dataset (train + test)
def create_data_mnist(path):
# Load both sets separately
X, y = load_mnist_dataset('train', path)
X_test, y_test = load_mnist_dataset('test', path)
# And return all the data
return X, y, X_test, y_test
import numpy as np
import nnfs
from nnfs.datasets import sine_data, spiral_data
import sys
nnfs.init()
# Dense layer
class Layer_Dense:
# Layer initialization
def __init__(self, n_inputs, n_neurons,
weight_regularizer_l1=0, weight_regularizer_l2=0,
bias_regularizer_l1=0, bias_regularizer_l2=0):
# Initialize weights and biases
# self.weights = 0.01 * np.random.randn(n_inputs, n_neurons)
self.weights = 0.1 * np.random.randn(n_inputs, n_neurons)
self.biases = np.zeros((1, n_neurons))
# Set regularization strength
self.weight_regularizer_l1 = weight_regularizer_l1
self.weight_regularizer_l2 = weight_regularizer_l2
self.bias_regularizer_l1 = bias_regularizer_l1
self.bias_regularizer_l2 = bias_regularizer_l2
# Forward pass
def forward(self, inputs, training):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs, weights and biases
self.output = np.dot(inputs, self.weights) + self.biases
# Backward pass
def backward(self, dvalues):
# Gradients on parameters
self.dweights = np.dot(self.inputs.T, dvalues)
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# Gradients on regularization
# L1 on weights
if self.weight_regularizer_l1 > 0:
dL1 = np.ones_like(self.weights)
dL1[self.weights < 0] = -1
self.dweights += self.weight_regularizer_l1 * dL1
# L2 on weights
if self.weight_regularizer_l2 > 0:
self.dweights += 2 * self.weight_regularizer_l2 * self.weights
# L1 on biases
if self.bias_regularizer_l1 > 0:
dL1 = np.ones_like(self.biases)
dL1[self.biases < 0] = -1
self.dbiases += self.bias_regularizer_l1 * dL1
# L2 on biases
if self.bias_regularizer_l2 > 0:
self.dbiases += 2 * self.bias_regularizer_l2 * self.biases
# Gradient on values
self.dinputs = np.dot(dvalues, self.weights.T)
# Dropout
class Layer_Dropout:
# Init
def __init__(self, rate):
# Store rate, we invert it as for example for dropout
# of 0.1 we need success rate of 0.9
self.rate = 1 - rate
# Forward pass
def forward(self, inputs, training):
# Save input values
self.inputs = inputs
# If not in the training mode - return values
if not training:
self.output = inputs.copy()
return
# Generate and save scaled mask
self.binary_mask = np.random.binomial(1, self.rate, size=inputs.shape) / self.rate
# Apply mask to output values
self.output = inputs * self.binary_mask
# Backward pass
def backward(self, dvalues):
# Gradient on values
self.dinputs = dvalues * self.binary_mask
# Input "layer"
class Layer_Input:
# Forward pass
def forward(self, inputs, training):
self.output = inputs
# ReLU activation
class Activation_ReLU:
# Forward pass
def forward(self, inputs, training):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs
self.output = np.maximum(0, inputs)
# Backward pass
def backward(self, dvalues):
# Since we need to modify original variable,
# let's make a copy of values first
self.dinputs = dvalues.copy()
# Zero gradient where input values were negative
self.dinputs[self.inputs <= 0] = 0
# Calculate predictions for outputs
def predictions(self, outputs):
return outputs
# Softmax activation
class Activation_Softmax:
# Forward pass
def forward(self, inputs, training):
# Remember input values
self.inputs = inputs
# Get unnormalized probabilities
exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
# Normalize them for each sample
probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
self.output = probabilities
# Backward pass
def backward(self, dvalues):
# Create uninitialized array
self.dinputs = np.empty_like(dvalues)
# Enumerate outputs and gradients
for index, (single_output, single_dvalues) in enumerate(zip(self.output, dvalues)):
# Flatten output array
single_output = single_output.reshape(-1, 1)
# Calculate Jacobian matrix of the output and
jacobian_matrix = np.diagflat(single_output) - np.dot(single_output, single_output.T)
# Calculate sample-wise gradient
# and add it to the array of sample gradients
self.dinputs[index] = np.dot(jacobian_matrix, single_dvalues)
# Calculate predictions for outputs
def predictions(self, outputs):
return np.argmax(outputs, axis=1)
# Sigmoid activation
class Activation_Sigmoid:
# Forward pass
def forward(self, inputs, training):
# Save input and calculate/save output
# of the sigmoid function
self.inputs = inputs
self.output = 1 / (1 + np.exp(-inputs))
# Backward pass
def backward(self, dvalues):
# Derivative - calculates from output of the sigmoid function
self.dinputs = dvalues * (1 - self.output) * self.output
# Calculate predictions for outputs
def predictions(self, outputs):
return (outputs > 0.5) * 1
# Linear activation
class Activation_Linear:
# Forward pass
def forward(self, inputs, training):
# Just remember values
self.inputs = inputs
self.output = inputs
# Backward pass
def backward(self, dvalues):
# derivative is 1, 1 * dvalues = dvalues - the chain rule
self.dinputs = dvalues.copy()
# Calculate predictions for outputs
def predictions(self, outputs):
return outputs
# SGD optimizer
class Optimizer_SGD:
# Initialize optimizer - set settings,
# learning rate of 1. is default for this optimizer
def __init__(self, learning_rate=1., decay=0., momentum=0.):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.momentum = momentum
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If we use momentum
if self.momentum:
# If layer does not contain momentum arrays, create them
# filled with zeros
if not hasattr(layer, 'weight_momentums'):
layer.weight_momentums = np.zeros_like(layer.weights)
# If there is no momentum array for weights
# The array doesn't exist for biases yet either.
layer.bias_momentums = np.zeros_like(layer.biases)
# Build weight updates with momentum - take previous
# updates multiplied by retain factor and update with
# current gradients
weight_updates = self.momentum * layer.weight_momentums - self.current_learning_rate * layer.dweights
layer.weight_momentums = weight_updates
# Build bias updates
bias_updates = self.momentum * layer.bias_momentums - self.current_learning_rate * layer.dbiases
layer.bias_momentums = bias_updates
# Vanilla SGD updates (as before momentum update)
else:
weight_updates = -self.current_learning_rate * layer.dweights
bias_updates = -self.current_learning_rate * layer.dbiases
# Update weights and biases using either
# vanilla or momentum updates
layer.weights += weight_updates
layer.biases += bias_updates
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adagrad optimizer
class Optimizer_Adagrad:
# Initialize optimizer - set settings
def __init__(self, learning_rate=1., decay=0., epsilon=1e-7):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache += layer.dweights**2
layer.bias_cache += layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# RMSprop optimizer
class Optimizer_RMSprop:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, rho=0.9):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.rho = rho
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache = self.rho * layer.weight_cache + (1 - self.rho) * layer.dweights**2
layer.bias_cache = self.rho * layer.bias_cache + (1 - self.rho) * layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adam optimizer
class Optimizer_Adam:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, beta_1=0.9, beta_2=0.999):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.beta_1 = beta_1
self.beta_2 = beta_2
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_momentums = np.zeros_like(layer.weights)
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_momentums = np.zeros_like(layer.biases)
layer.bias_cache = np.zeros_like(layer.biases)
# Update momentum with current gradients
layer.weight_momentums = self.beta_1 * layer.weight_momentums + (1 - self.beta_1) * layer.dweights
layer.bias_momentums = self.beta_1 * layer.bias_momentums + (1 - self.beta_1) * layer.dbiases
# Get corrected momentum
# self.iteration is 0 at first pass
# and we need to start with 1 here
weight_momentums_corrected = layer.weight_momentums / (1 - self.beta_1 ** (self.iterations + 1))
bias_momentums_corrected = layer.bias_momentums / (1 - self.beta_1 ** (self.iterations + 1))
# Update cache with squared current gradients
layer.weight_cache = self.beta_2 * layer.weight_cache + (1 - self.beta_2) * layer.dweights**2
layer.bias_cache = self.beta_2 * layer.bias_cache + (1 - self.beta_2) * layer.dbiases**2
# Get corrected cache
weight_cache_corrected = layer.weight_cache / (1 - self.beta_2 ** (self.iterations + 1))
bias_cache_corrected = layer.bias_cache / (1 - self.beta_2 ** (self.iterations + 1))
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * weight_momentums_corrected / (np.sqrt(weight_cache_corrected) + self.epsilon)
layer.biases += -self.current_learning_rate * bias_momentums_corrected / (np.sqrt(bias_cache_corrected) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Common loss class
class Loss:
# Regularization loss calculation
def regularization_loss(self):
# 0 by default
regularization_loss = 0
# Calculate regularization loss
# iterate all trainable layers
for layer in self.trainable_layers:
# L1 regularization - weights
# calculate only when factor greater than 0
if layer.weight_regularizer_l1 > 0:
regularization_loss += layer.weight_regularizer_l1 * np.sum(np.abs(layer.weights))
# L2 regularization - weights
if layer.weight_regularizer_l2 > 0:
regularization_loss += layer.weight_regularizer_l2 * np.sum(layer.weights * layer.weights)
# L1 regularization - biases
# calculate only when factor greater than 0
if layer.bias_regularizer_l1 > 0:
regularization_loss += layer.bias_regularizer_l1 * np.sum(np.abs(layer.biases))
# L2 regularization - biases
if layer.bias_regularizer_l2 > 0:
regularization_loss += layer.bias_regularizer_l2 * np.sum(layer.biases * layer.biases)
return regularization_loss
# Set/remember trainable layers
def remember_trainable_layers(self, trainable_layers):
self.trainable_layers = trainable_layers
# Calculates the data and regularization losses
# given model output and ground truth values
def calculate(self, output, y, *, include_regularization=False):
# Calculate sample losses
sample_losses = self.forward(output, y)
# Calculate mean loss
data_loss = np.mean(sample_losses)
# Add accumulated sum of losses and sample count
self.accumulated_sum += np.sum(sample_losses)
self.accumulated_count += len(sample_losses)
# If just data loss - return it
if not include_regularization:
return data_loss
# Return the data and regularization losses
return data_loss, self.regularization_loss()
# Calculates accumulated loss
def calculate_accumulated(self, *, include_regularization=False):
# Calculate mean loss
data_loss = self.accumulated_sum / self.accumulated_count
# If just data loss - return it
if not include_regularization:
return data_loss
# Return the data and regularization losses
return data_loss, self.regularization_loss()
# Reset variables for accumulated loss
def new_pass(self):
self.accumulated_sum = 0
self.accumulated_count = 0
# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Number of samples in a batch
samples = len(y_pred)
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Probabilities for target values -
# only if categorical labels
if len(y_true.shape) == 1:
correct_confidences = y_pred_clipped[
range(samples),
y_true
]
# Mask values - only for one-hot encoded labels
elif len(y_true.shape) == 2:
correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)
# Losses
negative_log_likelihoods = -np.log(correct_confidences)
return negative_log_likelihoods
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of labels in every sample
# We'll use the first sample to count them
labels = len(dvalues[0])
# If labels are sparse, turn them into one-hot vector
if len(y_true.shape) == 1:
y_true = np.eye(labels)[y_true]
# Calculate gradient
self.dinputs = -y_true / dvalues
# Normalize gradient
self.dinputs = self.dinputs / samples
# Softmax classifier - combined Softmax activation
# and cross-entropy loss for faster backward step
class Activation_Softmax_Loss_CategoricalCrossentropy():
# # Creates activation and loss function objects
# def __init__(self):
# self.activation = Activation_Softmax()
# self.loss = Loss_CategoricalCrossentropy()
# # Forward pass
# def forward(self, inputs, y_true):
# # Output layer's activation function
# self.activation.forward(inputs)
# # Set the output
# self.output = self.activation.output
# # Calculate and return loss value
# return self.loss.calculate(self.output, y_true)
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# If labels are one-hot encoded,
# turn them into discrete values
if len(y_true.shape) == 2:
y_true = np.argmax(y_true, axis=1)
# Copy so we can safely modify
self.dinputs = dvalues.copy()
# Calculate gradient
self.dinputs[range(samples), y_true] -= 1
# Normalize gradient
self.dinputs = self.dinputs / samples
# Binary cross-entropy loss
class Loss_BinaryCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Calculate sample-wise loss
sample_losses = -(y_true * np.log(y_pred_clipped) + (1 - y_true) * np.log(1 - y_pred_clipped))
sample_losses = np.mean(sample_losses, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
clipped_dvalues = np.clip(dvalues, 1e-7, 1 - 1e-7)
# Calculate gradient
self.dinputs = -(y_true / clipped_dvalues - (1 - y_true) / (1 - clipped_dvalues)) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Mean Squared Error loss
class Loss_MeanSquaredError(Loss): # L2 loss
# Forward pass
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean((y_true - y_pred)**2, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Gradient on values
self.dinputs = -2 * (y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Mean Absolute Error loss
class Loss_MeanAbsoluteError(Loss): # L1 loss
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean(np.abs(y_true - y_pred), axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Calculate gradient
self.dinputs = np.sign(y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Common accuracy class
class Accuracy:
# Calculates an accuracy
# given predictions and ground truth values
def calculate(self, predictions, y):
# Get comparison results
comparisons = self.compare(predictions, y)
# Calculate an accuracy
accuracy = np.mean(comparisons)
# Add accumulated sum of matching values and sample count
self.accumulated_sum += np.sum(comparisons)
self.accumulated_count += len(comparisons)
# Return accuracy
return accuracy
# Calculates accumulated accuracy
def calculate_accumulated(self):
# Calculate an accuracy
accuracy = self.accumulated_sum / self.accumulated_count
# Return the data and regularization losses
return accuracy
# Reset variables for accumulated accuracy
def new_pass(self):
self.accumulated_sum = 0
self.accumulated_count = 0
# Accuracy calculation for classification model
class Accuracy_Categorical(Accuracy):
# No initialization is needed
def init(self, y):
pass
# Compares predictions to the ground truth values
def compare(self, predictions, y):
if len(y.shape) == 2:
y = np.argmax(y, axis=1)
return predictions == y
# Accuracy calculation for regression model
class Accuracy_Regression(Accuracy):
def __init__(self):
# Create precision property
self.precision = None
# Calculates precision value
# based on passed in ground truth
def init(self, y, reinit=False):
if self.precision is None or reinit:
self.precision = np.std(y) / 250
# Compares predictions to the ground truth values
def compare(self, predictions, y):
return np.absolute(predictions - y) < self.precision
# Model class
class Model:
def __init__(self):
# Create a list of network objects
self.layers = []
# Softmax classifier's output object
self.softmax_classifier_output = None
# Add objects to the model
def add(self, layer):
self.layers.append(layer)
# Set loss, optimizer and accuracy
def set(self, *, loss, optimizer, accuracy):
self.loss = loss
self.optimizer = optimizer
self.accuracy = accuracy
# Finalize the model
def finalize(self):
# Create and set the input layer
self.input_layer = Layer_Input()
# Count all the objects
layer_count = len(self.layers)
# Initialize a list containing trainable layers:
self.trainable_layers = []
# Iterate the objects
for i in range(layer_count):
# If it's the first layer,
# the previous layer object is the input layer
if i == 0:
self.layers[i].prev = self.input_layer
self.layers[i].next = self.layers[i+1]
# All layers except for the first and the last
elif i < layer_count - 1:
self.layers[i].prev = self.layers[i-1]
self.layers[i].next = self.layers[i+1]
# The last layer - the next object is the loss
# Also let's save aside the reference to the last object
# whose output is the model's output
else:
self.layers[i].prev = self.layers[i-1]
self.layers[i].next = self.loss
self.output_layer_activation = self.layers[i]
# If layer contains an attribute called "weights",
# it's a trainable layer -
# add it to the list of trainable layers
# We don't need to check for biases -
# checking for weights is enough
if hasattr(self.layers[i], 'weights'):
self.trainable_layers.append(self.layers[i])
# Update loss object with trainable layers
self.loss.remember_trainable_layers(self.trainable_layers)
# If output activation is Softmax and
# loss function is Categorical Cross-Entropy
# create an object of combined activation
# and loss function containing
# faster gradient calculation
if isinstance(self.layers[-1], Activation_Softmax) and isinstance(self.loss, Loss_CategoricalCrossentropy):
# Create an object of combined activation
# and loss functions
self.softmax_classifier_output = Activation_Softmax_Loss_CategoricalCrossentropy()
# Train the model
# def train(self, X, y, *, epochs=1, print_every=1, validation_data=None):
def train(self, X, y, *, epochs=1, batch_size=None, print_every=1, validation_data=None):
# Initialize accuracy object
self.accuracy.init(y)
# Default value if batch size is not being set
train_steps = 1
# If there is validation data passed,
# set default number of steps for validation as well
if validation_data is not None:
validation_steps = 1
# For better readability
X_val, y_val = validation_data
# Calculate number of steps
if batch_size is not None:
train_steps = len(X) // batch_size
# Dividing rounds down. If there are some remaining
# data, but not a full batch, this won't include it
# Add `1` to include this not full batch
if train_steps * batch_size < len(X):
train_steps += 1
if validation_data is not None:
validation_steps = len(X_val) // batch_size
# Dividing rounds down. If there are some remaining
# data, but nor full batch, this won't include it
# Add `1` to include this not full batch
if validation_steps * batch_size < len(X_val):
validation_steps += 1
# Main training loop
for epoch in range(1, epochs+1):
# Print epoch number
print(f'epoch: {epoch}')
# Reset accumulated values in loss and accuracy objects
self.loss.new_pass()
self.accuracy.new_pass()
# Iterate over steps
for step in range(train_steps):
# If batch size is not set -
# train using one step and full dataset
if batch_size is None:
batch_X = X
batch_y = y
# Otherwise slice a batch
else:
batch_X = X[step*batch_size:(step+1)*batch_size]
batch_y = y[step*batch_size:(step+1)*batch_size]
# Perform the forward pass
output = self.forward(batch_X, training=True)
# Calculate loss
data_loss, regularization_loss = self.loss.calculate(output, batch_y, include_regularization=True)
loss = data_loss + regularization_loss
# Get predictions and calculate an accuracy
predictions = self.output_layer_activation.predictions(output)
accuracy = self.accuracy.calculate(predictions, batch_y)
# Perform backward pass
self.backward(output, batch_y)
# Optimize (update parameters)
self.optimizer.pre_update_params()
for layer in self.trainable_layers:
self.optimizer.update_params(layer)
self.optimizer.post_update_params()
# Print a summary
if not step % print_every or step == train_steps - 1:
print(f'step: {step}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {self.optimizer.current_learning_rate}')
# Get and print epoch loss and accuracy
epoch_data_loss, epoch_regularization_loss = self.loss.calculate_accumulated(include_regularization=True)
epoch_loss = epoch_data_loss + epoch_regularization_loss
epoch_accuracy = self.accuracy.calculate_accumulated()
print(f'training, ' +
f'acc: {epoch_accuracy:.3f}, ' +
f'loss: {epoch_loss:.3f} (' +
f'data_loss: {epoch_data_loss:.3f}, ' +
f'reg_loss: {epoch_regularization_loss:.3f}), ' +
f'lr: {self.optimizer.current_learning_rate}')
# If there is the validation data
if validation_data is not None:
# Reset accumulated values in loss
# and accuracy objects
self.loss.new_pass()
self.accuracy.new_pass()
# Iterate over steps
for step in range(validation_steps):
# If batch size is not set -
# train using one step and full dataset
if batch_size is None:
batch_X = X_val
batch_y = y_val
# Otherwise slice a batch
else:
batch_X = X_val[step*batch_size:(step+1)*batch_size]
batch_y = y_val[step*batch_size:(step+1)*batch_size]
# Perform the forward pass
output = self.forward(batch_X, training=False)
# Calculate the loss
self.loss.calculate(output, batch_y)
# Get predictions and calculate an accuracy
predictions = self.output_layer_activation.predictions(output)
self.accuracy.calculate(predictions, batch_y)
# Get and print validation loss and accuracy
validation_loss = self.loss.calculate_accumulated()
validation_accuracy = self.accuracy.calculate_accumulated()
# Print a summary
print(f'validation, ' +
f'acc: {validation_accuracy:.3f}, ' +
f'loss: {validation_loss:.3f}')
# Performs forward pass
def forward(self, X, training):
# Call forward method on the input layer
# this will set the output property that
# the first layer in "prev" object is expecting
self.input_layer.forward(X, training)
# Call forward method of every object in a chain
# Pass output of the previous object as a parameter
for layer in self.layers:
layer.forward(layer.prev.output, training)
# "layer" is now the last object from the list,
# return its output
return layer.output
# Performs backward pass
def backward(self, output, y):
# If softmax classifier
if self.softmax_classifier_output is not None:
# First call backward method
# on the combined activation/loss
# this will set dinputs property
self.softmax_classifier_output.backward(output, y)
# Since we'll not call backward method of the last layer
# which is Softmax activation
# as we used combined activation/loss
# object, let's set dinputs in this object
self.layers[-1].dinputs = self.softmax_classifier_output.dinputs
# Call backward method going through
# all the objects but last
# in reversed order passing dinputs as a parameter
for layer in reversed(self.layers[:-1]):
layer.backward(layer.next.dinputs)
return
# First call backward method on the loss
# this will set dinputs property that the last
# layer will try to access shortly
self.loss.backward(output, y)
# Call backward method going through all the objects
# in reversed order passing dinputs as a parameter
for layer in reversed(self.layers):
layer.backward(layer.next.dinputs)
# Create dataset
X, y, X_test, y_test = create_data_mnist('fashion_mnist_images')
# Shuffle the training dataset
keys = np.array(range(X.shape[0]))
np.random.shuffle(keys)
X = X[keys]
y = y[keys]
# Scale and reshape samples
X = (X.reshape(X.shape[0], -1).astype(np.float32) - 127.5) / 127.5
X_test = (X_test.reshape(X_test.shape[0], -1).astype(np.float32) - 127.5) / 127.5
# Instantiate the model
model = Model()
# # Add layers
# model.add(Layer_Dense(X.shape[1], 64))
# model.add(Activation_ReLU())
# model.add(Layer_Dense(64, 64))
# model.add(Activation_ReLU())
# model.add(Layer_Dense(64, 10))
# model.add(Activation_Softmax())
# # Set loss, optimizer and accuracy objects
# model.set(
# loss=Loss_CategoricalCrossentropy(),
# optimizer=Optimizer_Adam(decay=5e-5),
# accuracy=Accuracy_Categorical()
# )
# # Finalize the model
# model.finalize()
# # Train the model
# model.train(X, y, validation_data=(X_test, y_test), epochs=5, batch_size=128, print_every=100)
# Add layers
model.add(Layer_Dense(X.shape[1], 128))
model.add(Activation_ReLU())
model.add(Layer_Dense(128, 128))
model.add(Activation_ReLU())
model.add(Layer_Dense(128, 10))
model.add(Activation_Softmax())
# Set loss, optimizer and accuracy objects
model.set(
loss=Loss_CategoricalCrossentropy(),
optimizer=Optimizer_Adam(decay=1e-3),
accuracy=Accuracy_Categorical()
)
# Finalize the model
model.finalize()
# Train the model
model.train(X, y, validation_data=(X_test, y_test), epochs=10, batch_size=128, print_every=100)本章的章节代码、更多资源和勘误表:https://nnfs.io/ch19