【排序算法】——快速排序

c.c8312025-03-21 8:51

目录

1.快速排序的核心思想

快速排序是排序算法中较为优异的一种，它的核心思想就是：选取一个数据作为基准值，然后遍历需要排序的数据，使这个基准值放到它该放的位置，再对剩下的子区间进行递归，最后所有的数据都会放到它该放的位置，就完成了排序

2.快速排序的实现方式

这里我们先默认选取每一次递归区间的最左边的元素作为基准值，当然这种选取方式其实在某些特殊的数据存在很大的问题（待会再讨论）

2.1 递归版本

2.1 hoare版本

a.思路：给定left指针(代表下标)和right指针，分别从数据的左边和右边进行遍历，left指针从左往右找大，right指针从右往左找小，这里的比较是与基准值

b.画图展示：

注意：这里可以先让left指针先走一步，让比较的次数减少，一定程度上优化了一点点


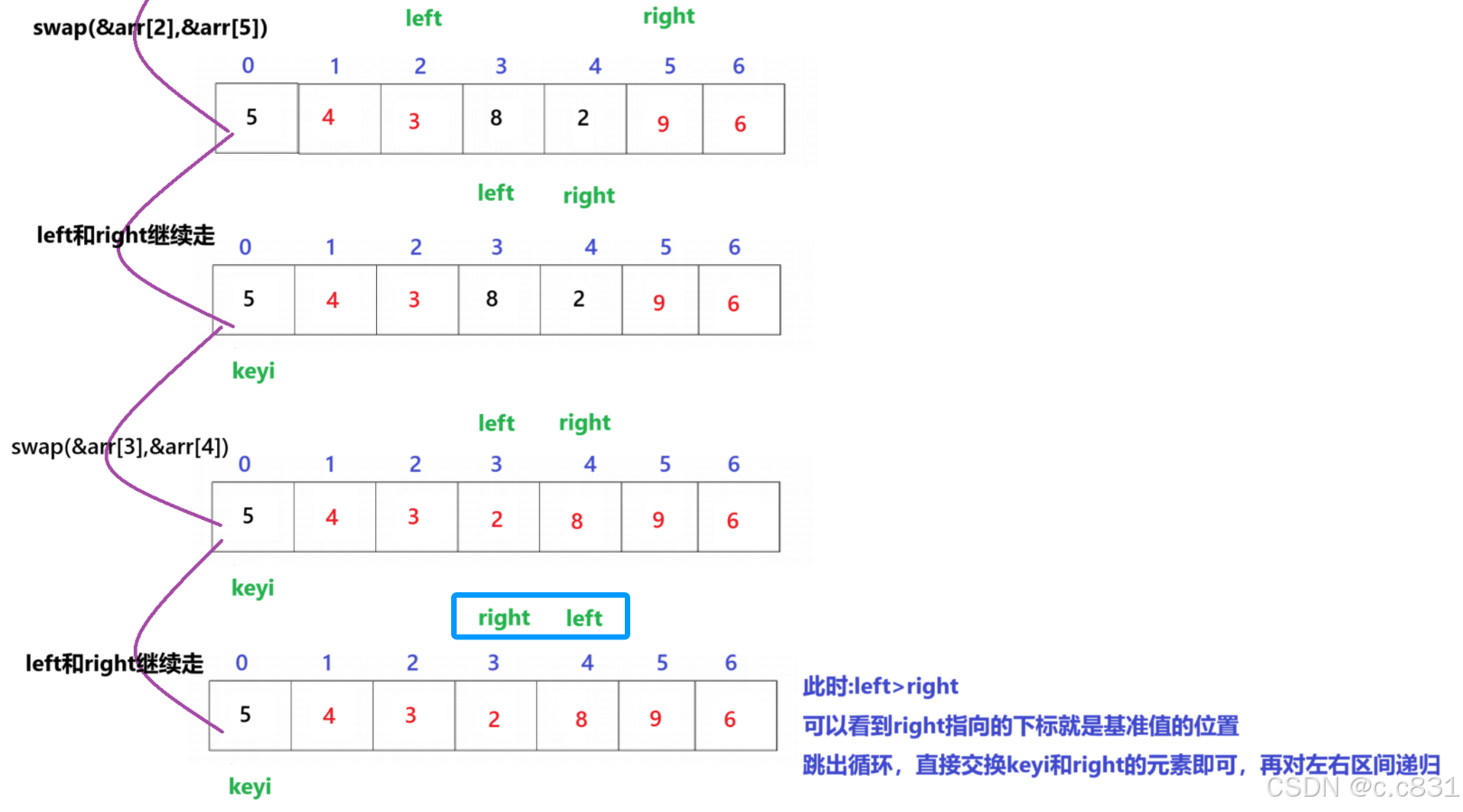
从画图的方式可知:>思路（续）：left指针和right指针找的过程当left比right大则停止，此时right指向的位置就是keyi该放的地方，交换即可

这里的递归左右区间的意思是：交换完keyi和right以后，该轮的keyi已经排序了，只要再对它的左右两段区间重复该一操作即可（递归），如图：

跳出循环的right会作为基准值返回，有了基准值就能得到左右区间的范围了

c. 代码实现：

这里将找基准值的方法和主体逻辑进行分离：

c 复制代码 
void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

//找基准值的方式
int  re_QuickSort(int* arr, int left, int right)
{
	int keyi = left;
	++left;
	//这里left与right取等也要进入循环
	//如果它们相遇时指向的值比基准值大，不进入循环指向的元素就没有放到该放的位置
	while (left <= right)
	{
		//right从右往左找比基准值小的数
		// left从左往右找比基准值大的数
		while (left <= right && arr[right] > arr[keyi])
		{
			right--;
		}

		while (left <= right && arr[left] < arr[keyi])
		{
			left++;
		}

		if (left <= right)
		{
		    //让left和right继续走
			Swap(&arr[right--], &arr[left++]);
		}
	}
	//在right下标和left下标交换后，left和right都会移动
	//可能在移动过程就不满足left <=right
	//所以让right与keyi进行交换应在循环外
	Swap(&arr[right], &arr[keyi]);
	return right;
}

//主体
void reQuickSort(int* arr, int left, int right)
{
	//保证区间是有效的
	if (left >= right)
	{
		return;
	}

	int keyi = re_QuickSort(arr, left, right);
	//将区间分为[left,keyi-1]   [keyi+1,right]
	reQuickSort(arr, left, keyi - 1);
	reQuickSort(arr, keyi + 1, right);

}

另：

在上面我们让left先走了一步，但是如果不让left先走一步，应该怎样处理呢？

如图：

注意：这里是为了画图方便在交换位置少了&操作符，它只是一段"伪代码"

此时如果再使用原来找keyi的方法只会让那两元素不断进行交换造成死递归，通过该图可以发现，这里只要right < keyi，此时的right在该段区间就是属于非法的，所以只需在跳出循环的时候判断两者即可，如果非法返回keyi

代码实现：

c 复制代码 
//left不++的基准值选取方法
int noneleft_Quick_sort(int* arr, int left, int right)
{
	int keyi = left;
	while (left <= right)
	{
		//right找小，left找大
		while (left <= right && arr[right] > arr[keyi])
		{
			right--;
		}

		while (left <= right && arr[left] < arr[keyi])
		{
			left++;
		}

		if (left <= right)
		{
			Swap(&arr[left++], &arr[right--]);
		}

	}
	if (right < keyi)
	{
		return keyi;
	}
	else
	{
		//尽量进行有效交换
		if (right != keyi)
		{
			Swap(&arr[keyi], &arr[right]);
		}
		return right;
	}

}

笔者建议：
从这个例子就可以看出，当我们想要改动代码的时候会造成不可预料的结果，如果要进行改动，需要弥补相应的措施，动手画图 + 调试会渐渐让你变得富有经验，耐心一点儿，问题总会解决的

2.2 lomuto版本

前言：该一实现方式又名双指针法，在初次接触的时候会感觉非常奇妙很难想，但是只要理解了背后的算法设计，就觉得还好

a.思路：

1.定义两个指针prev（left位置），pcur（left+1位置）

2.pcur在前面探路，只要pcur下标的元素比keyi小，就先让prev++，再与pcur++交换；如果比keyi大，直接++

3.跳出循环的时候，prev此时的指向就是基准值该待的位置，与keyi交换

b.代码实现：

c 复制代码 
//双指针版本
int dp_QuickSort(int* arr, int left, int right)
{
	int keyi = left;
	int prev = left, pcur = prev + 1;
	while (pcur <= right)
	{
		//pcur探路，找到比基准值小的数，先++prev然后与pcur交换
		//如果没有找到比基准值小的数，pcur++
		//pcur越界了，此时prev指向的就是keyi该待的位置
		if (arr[pcur] < arr[keyi] && ++prev != pcur)
		{
			Swap(&arr[prev], &arr[pcur]);
		}
		++pcur;
	}
	Swap(&arr[prev], &arr[keyi]);
	return prev;
}

void dpQuickSort(int* arr, int left, int right)
{
	if (left >= right)
	{
		return;
	}

	int keyi = dp_QuickSort(arr, left, right);
	dpQuickSort(arr, left, keyi - 1);
	dpQuickSort(arr, keyi + 1, right);

}

c.算法思想：
pcur对整个数组进行遍历，需要指向right(也是有效区间值)才结束，这里本质上其实就是对数组中进行三区间分化：

这里可以看出：从left~prev指向的区域都是≤keyi(5)的：

2.2 非递归版本（仅了解即可）

在非递归版本的快排实现中，我们需要借助一种数据结构：栈，主要的思路就是将区间放入栈中，并不断入栈出栈

代码实现：

c 复制代码 
void QuickSortNonR(int* arr, int left, int right)
{
	ST stack;
	STInit(&stack);

	//先将left和right入栈
	//注意栈的顺序：先进后出
	StackPush(&stack,right);
	StackPush(&stack,left);

	while (!StackEmpty(&stack))
	{
		int begin = StackTop(&stack);
		StackPop(&stack);
		int end = StackTop(&stack);
		StackPop(&stack);
		int prev = begin, pcur = begin + 1;
		int keyi = begin;
		while (pcur <= end)
		{
			//pcur探路，找到比基准值小的数，先++prev然后与pcur交换
			//如果没有找到比基准值小的数，pcur++
			//pcur越界了，此时prev指向的就是keyi该待的位置
			if (arr[pcur] < arr[keyi] && ++prev != pcur)
			{
				Swap(&arr[prev], &arr[pcur]);
			}
			++pcur;
		}
		Swap(&arr[prev], &arr[keyi]);
		keyi =  prev;


		//区间：[begin,keyi-1] [keyi+1,end]
		if (keyi + 1 < end)
		{
			StackPush(&stack,end);
			StackPush(&stack, keyi+1);
		}
		if (begin < keyi - 1)
		{
			StackPush(&stack, keyi - 1);
			StackPush(&stack,begin);
		}
	}

	STDestroy(&stack);
}

3.以上实现的快排方式的缺陷

上述快排的实现，我们都直接选取了最左边的元素为基准值，从各个图进行分析就可以看出快速排序一般来说就是一颗递归树，递归树的时间复杂度为O(n*logn)，但是碰到刚好完全有序的数据或者存有大量相同数据时，快排就会退化

本身就有序的情况：

这里以双指针版进行演示：

可以看到这里的快排就不是一颗递归树了，如果当存在大量数据时，效率就变得非常低，所以对于基准值的选取需要更进

4.快排的优化

优化大致就是对提到的两种情况进行相应的处理，尽量使得快排为一颗递归树

4.1 基准值优化

1.三数取中

要想让递归的区间从中间开始，就需要选取的基准值处在数据中不大也不小的状态，这样选取的基准值在第一轮时就会被放到中间，进而就大大缩减了递归的次数

代码实现：

c 复制代码 
//三数取中 -- 三个数中取中位数，基准值的选择尽量为数组中不大不小的元素
//如果只让基准值处于较大/较小的元素，递归的次数会增多，时间复杂度退化至o（n^2）
int midthree(int* arr, int left, int mid, int right)
{
	//0^1=1^0=1,0^0=1^1=0
	if ((arr[left] < arr[mid]) ^ (arr[left] < arr[right]))
	{
		//说明：ar[left]不大也不小
		return left;
	}
	else if ((arr[mid] < arr[left]) ^ (arr[mid] < arr[right]))
	{
		//说明：arr[mid]不大也不小
		return mid;
	}
	else
	{
		//说明：arr[right]不大也不小
		return right;
	}
}

优化后的快排------hoare版本

c 复制代码 
//三数取中版本------针对有序的数组做了优化，但是处理不了含有大量重复数据的情况
int  mid_QuickSort(int* arr, int left, int right)
{
	int med = midthree(arr, left, (left + right) / 2, right);
	//让中位数与最左边元素交换
	Swap(&arr[med], &arr[left]);
	int keyi = left;
	++left;

	//这里left与right取等也要进入循环
	//如果它们相遇时指向的值比基准值大，不进入循环指向的元素就没有放到该放的位置
	while (left <= right)
	{
		//right从右往左找比基准值小的数
		// left从左往右找比基准值大的数
		while (left <= right && arr[right] > arr[keyi])
		{
			right--;
		}

		while (left <= right && arr[left] < arr[keyi])
		{
			left++;
		}

		if (left <= right)
		{
			Swap(&arr[right--], &arr[left++]);
		}
	}
	//在right下标和left下标交换后，left和right都会移动
	//可能在移动过程就不满足left <=right
	//所以让right与keyi进行交换应在循环外
	Swap(&arr[right], &arr[keyi]);

	return right;
}

void midQuickSort(int* arr, int left, int right)
{
	if (left >= right)
	{
		return;
	}

	int keyi = mid_QuickSort(arr, left, right);

	midQuickSort(arr, left, keyi - 1);
	midQuickSort(arr, keyi + 1, right);

}

4.3 优化后的测试

这里以一道排序算法题作为测试：数组排序

优化前：

优化后：

2.随机数作基准值

这里还提供了另外一种方法作基准值：使用随机数，该数的范围在left~right之间，这种方式在算法导论中有进行严格的数学推到证明，有兴趣的读者可以自行了解

代码实现：

c 复制代码 
//设置种子
srand((unsigned int)time(NULL));
int keyi = arr[rand() % (right - left + 1) + left];

4.2 基准值分化区间优化

前言：当数组中含有大量相同数据时，我们实现的递归还是会退化，有了前面双指针算法的思想，可以衍生出另一个算法：三指针；双指针算法只是将区域分化成两部分：≤keyi、>keyi，但是如果再进一步划分区域：将=keyi的区域单独划分，那么快排的算法效率就会得到显著上升：

算法思想：
pleft：标记左区间，处理最后一个<keyi的位置
pright：标记右区间，处理第一个>keyi的位置
pcur：遍历整个数组

如图：

处理时的行为：

这里大于keyi时的情况已经在双指针讨论过了，这里照搬即可，等于keyi时，直接++即可，就剩下小于keyi时，我们用pright处理，这里只需先--pright，再与pcur交换，但是注意：pcur此时还不能动，因为--pright指向的元素还是不确定的，需要pcur进行判断，最后遍历完以后只需递归<keyi区间和>keyi区间，这种实现对于大量相同数据做了很好的处理

代码实现：

c 复制代码 
void tpQuickSort(int* arr, int left, int right)
{

	if (left >= right)
	{
		return;
	}
	//使用pleft、pright进行三路划分
	//采用随机取keyi的方式
	srand((unsigned int)time(NULL));
	int keyi = arr[rand() % (right - left + 1) + left];
	//int keyi = arr[left];
	int pleft = left - 1, pright = right + 1;
	int pcur = left;
	while (pcur < pright)
	{
		if (arr[pcur] < keyi)
		{
			Swap(&arr[++pleft], &arr[pcur++]);
		}
		else if (arr[pcur] > keyi)
		{
			Swap(&arr[--pright], &arr[pcur]);
		}
		else
		{
			pcur++;
		}
	}

	//(left,pleft)   (pleft+1,pright-1)   (pright,right)
 	// < keyi              ==keyi                 >keyi
	tpQuickSort(arr, left, pleft);
	tpQuickSort(arr, pright, right);
}
相关推荐
AI Echoes9 分钟前
大模型（LLMs）强化学习——RLHF及其变种
人工智能·深度学习·算法·机器学习·chatgpt
Dovis(誓平步青云）16 分钟前
精讲C++四大核心特性：内联函数加速原理、auto智能推导、范围for循环与空指针进阶
c语言·开发语言·c++·笔记·算法·学习方法
椰萝Yerosius1 小时前
[题解]2023CCPC黑龙江省赛 - Folder
算法
wang__123001 小时前
力扣2680题解
算法·leetcode·职场和发展
GGBondlctrl2 小时前
【leetcode】《BFS扫荡术：如何用广度优搜索征服岛屿问题》
算法·leetcode·bfs·宽度优先·图像渲染·岛屿的数量·被围绕的区域
容辞6 小时前
算法-贪婪算法
算法·贪心算法
Evand J6 小时前
MATLAB程序演示与编程思路，相对导航，四个小车的形式，使用集中式扩展卡尔曼滤波（fullyCN-EKF）
人工智能·算法
椰萝Yerosius8 小时前
[题解]2023CCPC黑龙江省赛 - Ethernet
算法·深度优先
IT猿手9 小时前
基于 Q-learning 的城市场景无人机三维路径规划算法研究，可以自定义地图，提供完整MATLAB代码
深度学习·算法·matlab·无人机·强化学习·qlearning·无人机路径规划
竹下为生11 小时前
LeetCode --- 448 周赛
算法·leetcode·职场和发展
热门推荐
01【分布式】Hadoop完全分布式的搭建（零基础）02从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑03KGG转MP3工具|非KGM文件|解密音频04YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】05【SpeedAI科研小助手】2分钟极速解决知网维普重复率、AIGC率过高，一键全文降！文件格式不变，公式都保留的！06西电B测-计算机网络综合实验(含验收问题)07最新 Kubernetes 集群部署 + flannel 网络插件（保姆级教程，最新 K8S 版本）08苍穹外卖面试总结09DeepSeek各版本说明与优缺点分析10Anaconda +Jupyter Notebook安装（2025最新版）