高级数据结构01BST树

我的sun&shine2025-03-28 20:55

文章目录

1.BST树介绍

cpp 复制代码 
// BST树.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include "pch.h"
// BST.cpp : 定义控制台应用程序的入口点。
//

#include <iostream>
#include <queue>
#include <stack>
#include <vector>
using namespace std;

/*
二叉树
*/

// BST树的实现
template<typename T>
class BSTree
{
public:
	BSTree() :_root(nullptr) {}
	// 非递归实现BST树的插入操作
	void noninsert(const T &val)
	{
		if (_root == nullptr)
		{
			_root = new BSTNode(val);
			return;
		}

		BSTNode *pre = nullptr;
		BSTNode *cur = _root;
		while (cur != nullptr)
		{
			pre = cur;
			if (val < cur->_data)
			{
				cur = cur->_left;
			}
			else if (val > cur->_data)
			{
				cur = cur->_right;
			}
			else
			{
				return;
			}
		}

		if (val < pre->_data)
		{
			pre->_left = new BSTNode(val);
		}
		else
		{
			pre->_right = new BSTNode(val);
		}
	}

	// 非递归实现BST树的删除操作
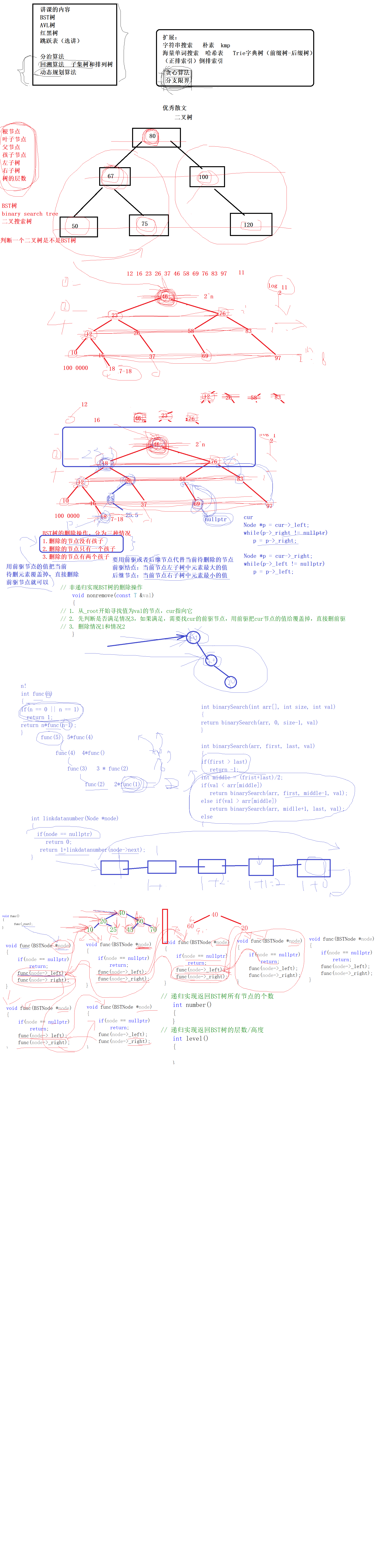
	void nonremove(const T &val)
	{
		// 1. 从_root开始寻找值为val的节点，cur指向它
		BSTNode *pre = nullptr;
		BSTNode *cur = _root;
		while (cur != nullptr)
		{
			if (val < cur->_data)
			{
				pre = cur;
				cur = cur->_left;
			}
			else if (val > cur->_data)
			{
				pre = cur;
				cur = cur->_right;
			}
			else
			{
				break;
			}
		}

		if (cur == nullptr)
			return;

		// 2. 先判断是否满足情况3，如果满足，需要找cur的前驱节点，用前驱把cur节点的值给覆盖掉，直接删前驱
		if (cur->_left != nullptr && cur->_right != nullptr)
		{
			BSTNode *old = cur;
			pre = cur;
			cur = cur->_left;
			while (cur->_right != nullptr)
			{
				pre = cur;
				cur = cur->_right;
			}
			old->_data = cur->_data;
		}
		// 3. 删除情况1和情况2   直接删除cur指针指向的节点就可以了
		BSTNode *child = cur->_left;
		if (child == nullptr)
		{
			child = cur->_right;
		}

		if (pre == nullptr) // cur指向的根节点
		{
			_root = child;
		}
		else
		{
			// 要把删除节点的孩子赋给cur父节点相应的地址域里面
			if (cur == pre->_left)
			{
				pre->_left = child;
			}
			else
			{
				pre->_right = child;
			}
		}
		delete cur;
	}

	// 实现对BST树的镜像翻转
	void mirror()
	{
		mirror(_root);
	}

	// 判断当前二叉树是不是一颗BST树
	bool isBSTree()
	{
		BSTNode *pre = nullptr;
		return isBSTree(_root, pre);
	}

	// 在当前BST树中，把满足区间[first, last]的所有元素找出来并打印
	void findAreaData(int first, int last)
	{
		vector<int> vec;
		findAreaData(_root, first, last, vec);
		for (int v : vec)
		{
			cout << v << " ";
		}
		cout << endl;
	}

	// 获取两个节点的最近公共祖先节点
	int getLCA(int val1, int val2)
	{
		BSTNode *p = getLCA(_root, val1, val2);
		if (p != nullptr)
		{
			return p->_data;
		}
		else
		{
			throw "no LCA node!";
		}
	}

	// 获取中序遍历倒数第k个节点的值
	int getLastKValue(int k) // LVR    RVL
	{
		int i = 0;
		BSTNode *p = getLastKValue(_root, k, i);
		if (p != nullptr)
		{
			return p->_data;
		}
		else
		{
			throw "no last k value, k is invalid!";
		}
	}

	// 判断参数tree是否是当前BST树的一颗子树，是返回true，否则返回false
	bool isChildTree(const BSTree<T> &tree)
	{
		if (_root == nullptr)
			return false;
		BSTNode *cur = _root;
		while (cur != nullptr)
		{
			if (tree._root->_data > cur->_data)
			{
				cur = cur->_right;
			}
			else if (tree._root->_data < cur->_data)
			{
				cur = cur->_left;
			}
			else
			{
				break;
			}
		}
		if (cur == nullptr)
			return false;

		return isChildTree(cur, tree._root);
	}

	// 一直一颗BST树的前序遍历结果pre数组，和中序遍历结果in数组，重建二叉树
	void rebuildBSTree(int pre[], int len1, int in[], int len2)
	{
		this->_root = rebuildBSTree(pre, 0, len1-1, in, 0, len2-1);
	}

	// 递归实现返回BST树所有节点的个数
	int number()
	{
		return number(_root);
	}

	// 递归实现返回BST树的层数/高度
	int level()
	{
		return level(_root);
	}

	// 递归实现前序遍历  
	void preOrder()
	{
		cout << "递归实现前序遍历:";
		preOrder(_root);
		cout << endl;
	}

	// 递归实现中序遍历
	void inOrder()
	{
		cout << "递归实现中序遍历:";
		inOrder(_root);
		cout << endl;
	}

	// 递归实现后序遍历
	void postOrder()
	{
		cout << "递归实现后序遍历:";
		postOrder(_root);
		cout << endl;
	}

	// 递归实现层序遍历
	void levelOrder()
	{
		cout << "递归实现层序遍历:";
		int l = level(_root);
		for (int i = 0; i < l; ++i)
		{
			levelOrder(_root, i);
		}
		cout << endl;
	}

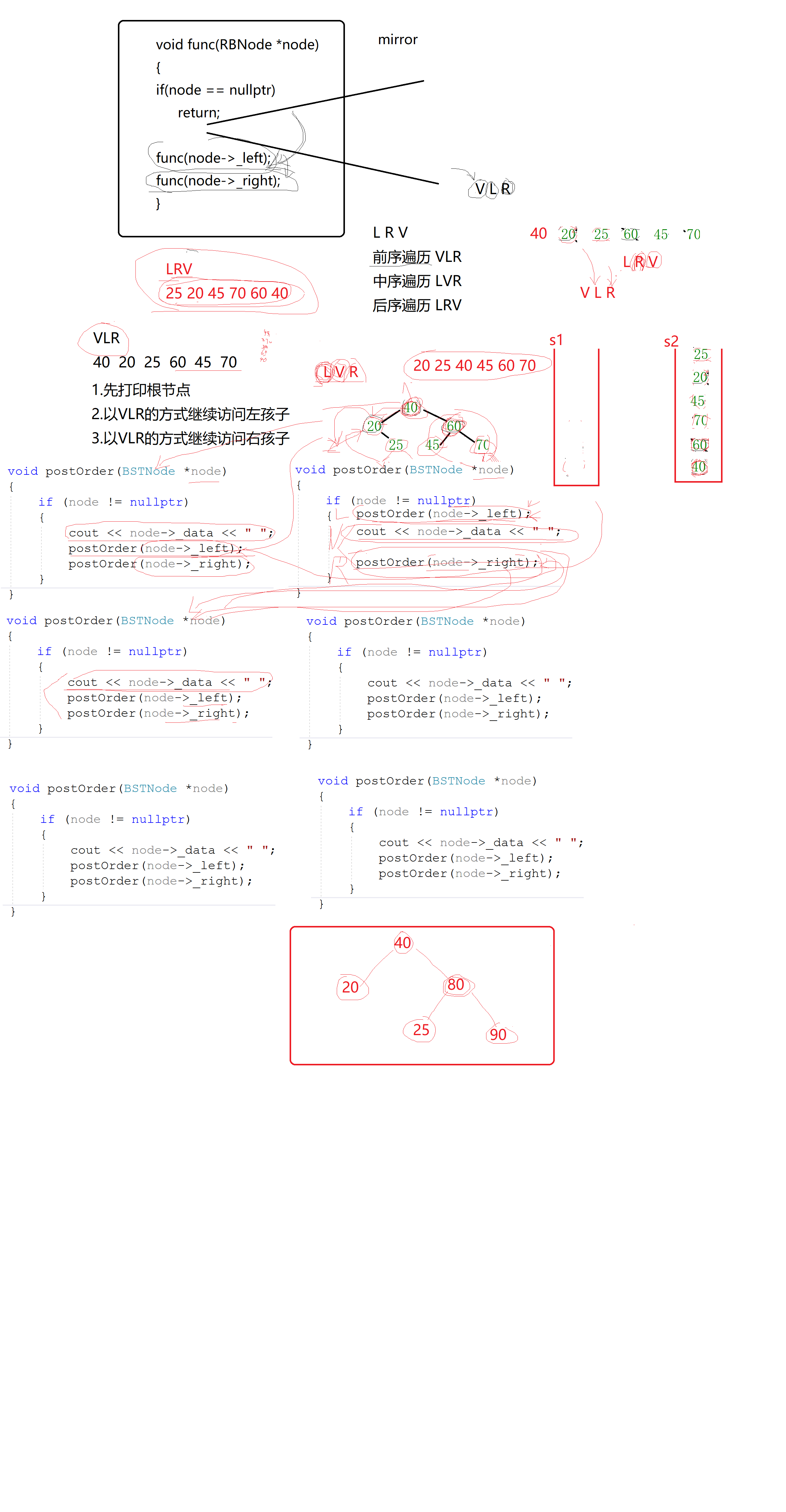
	// 非递归实现BST的前序遍历  VLR
	void nonpreOrder()
	{
		if (_root == nullptr)
			return;

		stack<BSTNode*> s;
		s.push(_root);

		while (!s.empty()) // VLR
		{
			BSTNode *top = s.top();
			s.pop();
			cout << top->_data << " "; // 打印V元素

			if (top->_right != nullptr) // 把右孩子先入栈
			{
				s.push(top->_right);
			}

			if (top->_left != nullptr) // 把左孩子后入栈，左孩子就在栈顶
			{
				s.push(top->_left);
			}
		}
		cout << endl;
	}

	// 非递归实现BST的中序遍历 LVR
	void noninOrder()
	{
		if (_root == nullptr)
			return;

		stack<BSTNode*> s;
		BSTNode *cur = _root;
		while (!s.empty() || cur != nullptr)
		{
			if(cur != nullptr)
			{
				s.push(cur);
				cur = cur->_left;
			}
			else
			{
				BSTNode *top = s.top();
				s.pop();
				cout << top->_data << " ";
				cur = top->_right;
			}
		}
		cout << endl;
	}

	// 非递归实现BST的后序遍历  LRV
	void nonpostOrder()
	{
		if (_root == nullptr)
			return;

		stack<BSTNode*> s1; // 辅助用的栈
		stack<BSTNode*> s2; // 存储后序遍历节点的栈
		s1.push(_root);

		while (!s1.empty())
		{
			BSTNode *top = s1.top();
			s1.pop();

			if (top->_left != nullptr)
			{
				s1.push(top->_left);
			}
			if (top->_right != nullptr)
			{
				s1.push(top->_right);
			}
			s2.push(top);
		}

		while (!s2.empty())
		{
			cout << s2.top()->_data << " ";
			s2.pop();
		}
		cout << endl;
	}

	// 非递归实现层序遍历(从根节点开始，一层一层按从左向右的顺序打印BST树节点的值)
	void nonlevelOrder()
	{
		// 1.如果_root为空，直接返回
		if (_root == nullptr)
			return;
		// 2._root -> queue
		queue<BSTNode*> que;
		que.push(_root);

		// 3.循环判断队列是否为空， 不为空取出队头元素，分别判断左右孩子是否为nullptr，不为空
		// 就要依次入队，然后打印队头元素，继续判断下一个队头元素
		while (!que.empty())
		{
			BSTNode *front = que.front();
			cout << front->_data << " ";
			que.pop();
			if (front->_left != nullptr)
			{
				que.push(front->_left);
			}
			if (front->_right != nullptr)
			{
				que.push(front->_right);
			}
		}
	}
public:
	// 定义BST树节点的类型
	struct BSTNode
	{
		BSTNode(T data = T())
			:_data(data)
			, _left(nullptr)
			, _right(nullptr)
		{}
		T _data;
		BSTNode *_left;
		BSTNode *_right;
	};

	void mirror(BSTNode *node)
	{
		if (node == nullptr)
			return;

		BSTNode *ptmp = node->_left;
		node->_left = node->_right;
		node->_right = ptmp;

		mirror(node->_left);
		mirror(node->_right);
	}

	// 以node为根节点，判断当前二叉树是不是BST树
	bool isBSTree(BSTNode *node, BSTNode *&pre)
	{
		if (node == nullptr)
		{
			return true;
		}

		if (!isBSTree(node->_left, pre))
		{
			return false;
		}
			
		if (pre != nullptr)
		{
			if (node->_data < pre->_data)
			{
				return false;
			}
		}
		pre = node;
			
		return isBSTree(node->_right, pre);
	}

	// 以node为根节点，中序遍历BST树，找满足区间[first,last]之间的元素
	void findAreaData(BSTNode *node, int first, int last, vector<int> &vec)
	{
		if (node == nullptr)
			return;

		findAreaData(node->_left, first, last, vec);

		if (node->_data > last)
		{
			return;
		}
		if (first <= node->_data && last >= node->_data)
		{
			vec.push_back(node->_data);
		}

		findAreaData(node->_right, first, last, vec);
	}

	// 以node为根节点，开始寻找val1和val2的LCA
	BSTNode* getLCA(BSTNode *node, int val1, int val2)
	{
		if (node == nullptr)
		{
			return nullptr;
		}
			
		if (val1 < node->_data && val2 < node->_data) 
		{
			return getLCA(node->_left, val1, val2);
		}
		else if (val1 > node->_data && val2 > node->_data)
		{
			return getLCA(node->_right, val1, val2);
		}
		else
		{
			return node;
		}
	}

	// LVR RVL 以node为根节点，找反向中序遍历的第K个节点
	BSTNode* getLastKValue(BSTNode *node, int k, int &i)
	{
		if (node == nullptr)
		{
			return nullptr;
		}

		BSTNode *p1 = getLastKValue(node->_right, k, i); // R
		if (p1 != nullptr)
		{
			return p1;
		}

		i++;
		if (k == i)
		{
			return node; // V
		}

		return getLastKValue(node->_left, k, i); // L
	}

	// 从father节点开始判断，是否全包含child的节点
	bool isChildTree(BSTNode *father, BSTNode *child)
	{
		if (father == nullptr && child == nullptr)
		{
			return true;
		}

		if (father == nullptr)
		{
			return false;
		}

		if (child == nullptr)
		{
			return true;
		}

		if (father->_data != child->_data)
		{
			return false;
		}

		return isChildTree(father->_left, child->_left)
			&& isChildTree(father->_right, child->_right);
	}

	/*
	               i                          j
	int pre[] = { 40， 20， 10， 25， 60， 50， 70 }; // VLR
	int in[] = { 10， 20， 25， 40， 50， 60， 70 }; // LVR
	              m             k
	*/
	BSTNode* rebuildBSTree(int pre[], int i, int j, int in[], int m, int n)
	{
		if (i > j || m > n)
		{
			return nullptr;
		}

		BSTNode *root = new BSTNode(pre[i]);
		for (int k = m; k <= n; ++k)
		{
			if (pre[i] == in[k]) // 中序遍历种找到根节点了
			{
				root->_left = rebuildBSTree(pre, i+1, i+(k-m), in, m, k-1);
				root->_right = rebuildBSTree(pre, i+(k - m)+1, j, in, k+1, n);
				break;
			}
		}
		return root;
	}

	// 返回以node为根节点的子树节点的总数
	int number(BSTNode *node)
	{
		if (node == nullptr)
			return 0;
		return 1 + number(node->_left) + number(node->_right);
	}

	// 返回以node为根节点的树的层数/高度
	int level(BSTNode *node)
	{
		if (node == nullptr)
		{
			return 0;
		}
		else
		{
			int left = level(node->_left);
			int right = level(node->_right);
			return left > right ? left + 1 : right + 1;
		}
	}

	// 以node为根节点(V)前序遍历BST树
	void preOrder(BSTNode *node)
	{
		if (node != nullptr)
		{
			cout << node->_data << " ";
			preOrder(node->_left);
			preOrder(node->_right);
		}
	}

	// 以node为根节点(V)中序遍历BST树
	void inOrder(BSTNode *node)
	{
		if (node != nullptr)
		{
			inOrder(node->_left);
			cout << node->_data << " ";
			inOrder(node->_right);
		}
	}

	// 以node为根节点(V)后序遍历BST树 L R V
	void postOrder(BSTNode *node)
	{
		if (node != nullptr)
		{
			postOrder(node->_left);
			postOrder(node->_right);
			cout << node->_data << " ";
		}
	}

	// 打印以node为根节点的树的层序遍历
	void levelOrder(BSTNode *node, int k) // 2
	{
		if (node != nullptr)
		{
			if (k == 0)
			{
				cout << node->_data << " ";
				return;
			}
			levelOrder(node->_left, k - 1);
			levelOrder(node->_right, k - 1);
		}
	}

	BSTNode *_root; // 指向树的根节点
};
int main(int argc, char* argv[])
{
	/*
	BSTree<int> bst;

	int arr[] = { 40,20,60,10,25,50,70 };
	for (int i = 0; i < 7; ++i)
	{
		bst.noninsert(arr[i]);
	}

	bst.findAreaData(20, 40);
	bst.preOrder();
	bst.inOrder();
	int lca = bst.getLCA(10, 20);
	cout << "LCA:" << lca << endl;

	int kval = bst.getLastKValue(4);
	cout << "kval:" << kval << endl;
	*/

	int pre[] = { 40,20,10,25,60,50,70 }; // VLR
	int in[] = { 10,20,25,40,50,60,70 }; // LVR
	BSTree<int> bst1;
	bst1.rebuildBSTree(pre, sizeof(pre)/sizeof(pre[0]),
		in, sizeof(in)/sizeof(in[0]));

	bst1.preOrder();
	bst1.inOrder();
	
#if 0
	BSTree<int> bst;

	BSTree<int>::BSTNode *n1 = new BSTree<int>::BSTNode(40);
	BSTree<int>::BSTNode *n2 = new BSTree<int>::BSTNode(20);
	BSTree<int>::BSTNode *n3 = new BSTree<int>::BSTNode(60);
	BSTree<int>::BSTNode *n4 = new BSTree<int>::BSTNode(55);
	BSTree<int>::BSTNode *n5 = new BSTree<int>::BSTNode(45);
	BSTree<int>::BSTNode *n6 = new BSTree<int>::BSTNode(70);

	bst._root = n1;
	n1->_left = n2;
	n1->_right = n3;
	n3->_left = n4;
	n2->_right = n6;
	cout << bst.isBSTree() << endl;
#endif

#if 0
	BSTree<int> bst;

	/*
		   40
	 20             60
10      25     50         70


   15

       60
	50     70
	  55

	   25   45     70

		  40
	 60       20
		70     45   25
	*/
	bst.noninsert(40);
	bst.noninsert(20);
	bst.noninsert(60);
	bst.noninsert(25);
	bst.noninsert(45);
	bst.noninsert(70);
	bst.nonlevelOrder();
	cout << endl;
	//bst.mirror();
	//bst.nonlevelOrder();
	cout << bst.level() << endl;
	cout << endl;

	bst.preOrder();
	bst.nonpreOrder();
	bst.inOrder();
	bst.noninOrder();
	bst.postOrder();
	bst.nonpostOrder();
	bst.levelOrder();
	//bst.nonremove(20);
	//bst.nonlevelOrder();
	//cout<<endl;
#endif
	return 0;
}

2.数据结构

3.遍历方式

相关推荐
虾球xz14 分钟前
游戏引擎学习第244天: 完成异步纹理下载
c++·学习·游戏引擎
矛取矛求21 分钟前
C++区别于C语言的提升用法（万字总结）
c语言·c++
mit6.82422 分钟前
[贪心_7] 最优除法 | 跳跃游戏 II | 加油站
数据结构·算法·leetcode
keep intensify24 分钟前
通讯录完善版本（详细讲解+源码）
c语言·开发语言·数据结构·算法
ephemerals__27 分钟前
【c++11】c++11新特性（下）（可变参数模板、default和delete、容器新设定、包装器）
开发语言·c++
shix .30 分钟前
2025年PTA天梯赛正式赛 | 算法竞赛，题目详解
数据结构·算法
风铃儿~39 分钟前
Java面试高频问题（26-28）
java·算法·面试
wuqingshun31415941 分钟前
蓝桥杯 4. 卡片换位
算法·职场和发展·蓝桥杯
江沉晚呤时43 分钟前
深入了解C# List集合及两种常见排序算法：插入排序与堆排序
windows·sql·算法·oracle·c#·排序算法·mybatis
egoist20231 小时前
【C++指南】告别C字符串陷阱：如何实现封装string？
开发语言·数据结构·c++·c++11·string·auto·深/浅拷贝
热门推荐
01KGG转MP3工具|非KGM文件|解密音频02从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑03我决定放弃搞 Java 了04Coze扣子平台完整体验和实践（附国内和国际版对比）05YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】06DeepSeek各版本说明与优缺点分析07yolov8，yolo11，yolo12 服务器训练到部署全流程 笔记08苍穹外卖面试总结09如何在WPS和Word/Excel中直接使用DeepSeek功能10【2025年最新】OpenWrt 更换国内源的指南（图形界面版)