数据结构-链表
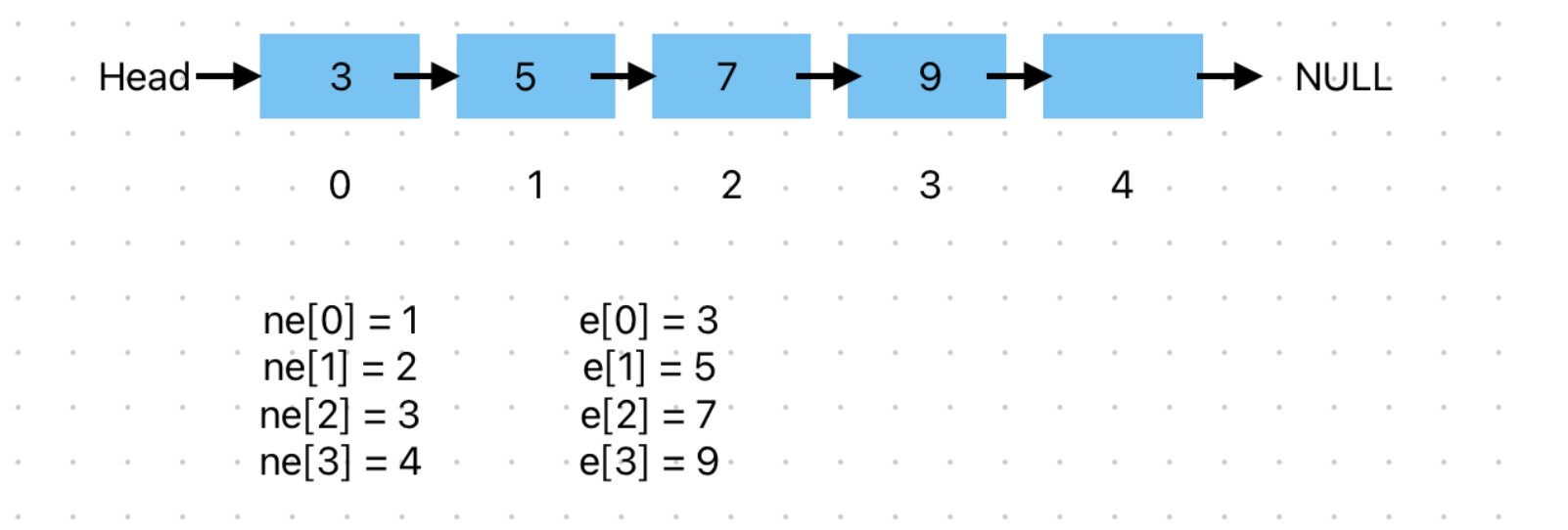
单链表
#include<iostream>
using namespace std;
const int N = 100010;
int head,e[N],ne[N],idx;
void init()
{
head = -1;
idx = 0;
}
void add_to_head(int x)
{
e[idx] = x;
ne[idx] = head;
head = idx;
idx++;
}
void add(int k,int x)
{
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
void remove(int k)
{
ne[k] = ne[ne[k]];
}
int main()
{
int m;
cin >> m;
init();
while(m--)
{
int k,x;
char op;
cin >> op;
if(op == 'H')
{
cin >> x;
add_to_head(x);
}
else if(op == 'D')
{
cin >> k;
if(k == 0) head = ne[head];
else remove(k-1);
}
else{
cin >> k >> x;
add(k-1,x);
}
}
for(int i = head;i!=-1;i=ne[i])
cout << e[i] << ' ';
cout << endl;
return 0;
}双链表
-
之所以在 "D", "IL", "IR" 要用 k+1 的原因是 双链表的起始点是2. 所以,每个插入位置k的真实位置应该为 k-1+2 = k+1 (在单链表中为 k-1)。
-
0, 1 节点的作用是边界。0为左边界,1为右边界。他俩在这里有点类似保留字的作用。正因如此,我们的idx也是从2开始
-
最后遍历输出结果的 for (int i = rn[0]; i != 1; i = rn[i])。从 rn[0] 开始是因为 0 为左边界,而终止条件 i==1是因为1为右边界(如果碰到,说明已经遍历完毕)
-

#include<iostream>
using namespace std;
const int N = 100010;
int m;
int e[N],l[N],r[N],idx;
void insert(int a,int x)
{
e[idx] = x;
r[idx] = r[a];
l[idx] = a;
l[r[a]] = idx;
r[a] = idx++;
}
void remove(int a)
{
r[l[a]] = r[a];
l[r[a]] = l[a];
}
int main()
{
int m;
cin >> m;
r[0] = 1,l[1] = 0;
idx = 2;
while(m--)
{
string op;
cin >> op;
int a,x;
if(op == "L")
{
cin >> x;
insert(0,x);
}
else if(op == "R")
{
cin >> x;
insert(l[1],x);
}
else if(op == "D")
{
cin >> a;
remove(a-1+2);
}
else if(op == "IL")
{
cin >> a >> x;
insert(l[a+1],x);
}
else if(op == "IR")
{
cin >> a >> x;
insert(a+1,x);
}
}
for(int i = r[0];i!=1;i=r[i])
cout << e[i] << ' ';
cout << endl;
return 0;
}
模拟栈(先进后出)
#include<iostream>
using namespace std;
const int N = 100010;
int m;
int stk[N],tt = 0;
int main()
{
cin >> m;
while(m--)
{
string op;
int x;
cin >> op;
if(op == "push")
{
cin >> x;
stk[++ tt] = x;
}
else if(op == "pop")
tt--;
else if(op == "empty")
cout << (tt ? "NO" : "YES") << endl;
else cout << stk[tt] << endl;
}
return 0;
}模拟队列(先进先出)
三木运算符
tt ? "NO" : "YES"意思:如果 tt 为true 结果是 "NO"
如果 tt 是false 结果是"YES",其中,在c++中,false 等价于0
#include<iostream>
using namespace std;
const int N = 100010;
int m;
int q[N],tt = -1,hh = 0;
int main()
{
int m;
cin >> m;
while(m--)
{
string op;
cin >> op;
int x;
if(op == "push")
{
cin >> x;
q[++tt] = x;
}
else if(op == "pop")
{
hh++;
}
else if(op == "empty")
cout << (hh <= tt ? "NO" : "YES") << endl;
else
cout << q[hh] << endl;
}
return 0;
}单调栈
暴力做法:两重循环。暴力求解
#include<iostream>
using namespace std;
const int N = 100010;
int stk[N],tt = 0;
int main()
{
int n;
cin >> n;
while(n--)
{
int x;
cin >> x;
//如果栈顶元素大于当前待入栈元素,则出栈
while(tt && stk[tt] >= x)
tt--;
if(!tt)
cout << "-1";
else
cout << stk[tt];
stk[++tt] = x;
}
return 0;
}
//还有一种方法就是运用STL来做
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int n,x;
cin >> n;
vector<int> t;
while(n--)
{
cin >> x;
while(t.size() > 0 and t.back() >= x){
t.pop_back();
}
if(t.size() == 0)
{
cout << -1 << ' ';
}
else
cout << t.back() << ' ';
t.push_back(x);
}
return 0;
}滑动窗口
//如果用普通队列的话
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e6 + 10;
int a[N],n,k;
int main()
{
cin >> n >> k;
for(int i = 0;i<n;i++) cin >> a[i];
//求每个窗口的最小值
for(int i = 0;i<=n-k;++i){
int minv = a[i];
for(int j = i + 1;j < i + k;++j)
{
minv = min(minv,a[j]);
}
cout << minv << " ";
}
cout << endl;
//求每个窗口的最大值
for(int i = 0;i <= n-k;++i)
{
int maxv = a[i];
for(int j = i + 1;j < i + k;++j)
{
maxv = max(maxv,a[j]);
}
cout << maxv << " ";
}
cout << endl;
return 0;
}如果运用单调队列的话,会超时
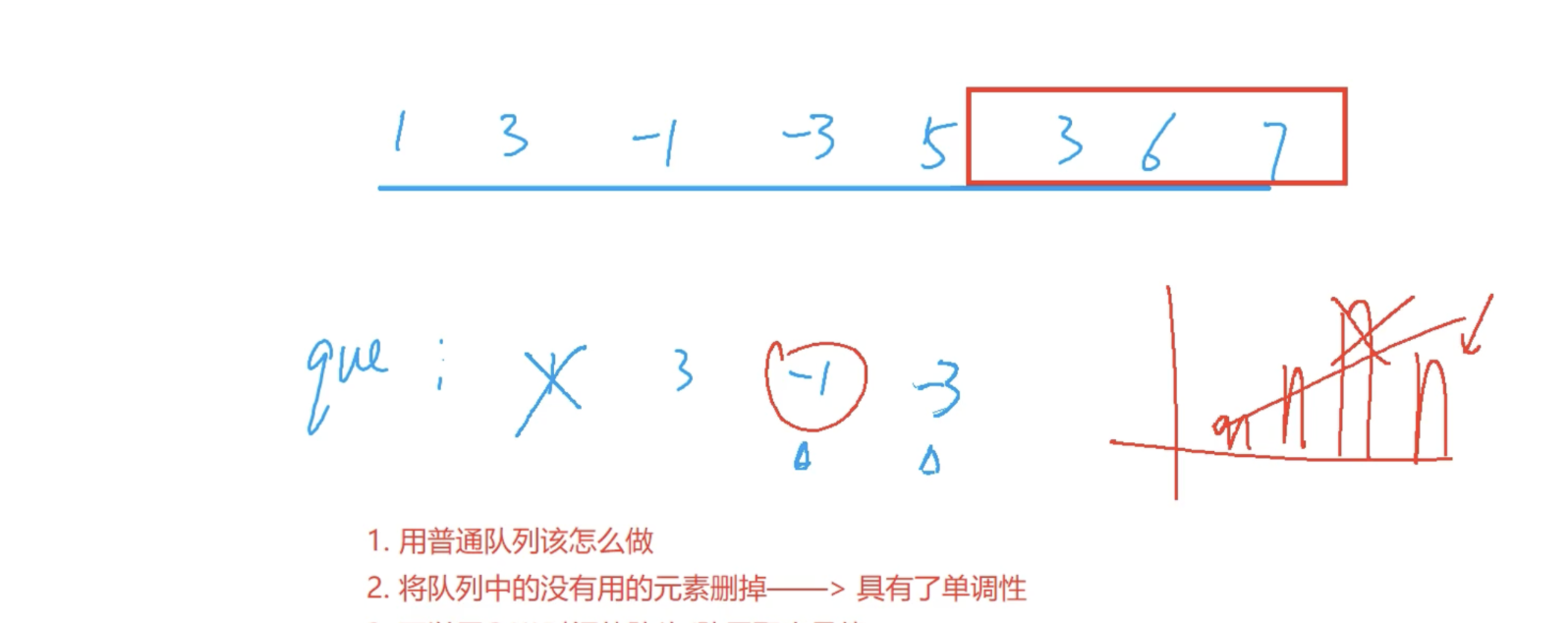
//运用双端队列
#include<iostream>
using namespace std;
const int N = 1000010;
//单调队列一般用双端队列保证其单调性.这里面的q数组表示下标,a数组表示数字
int a[N],q[N],n,k;
//队头与队尾,在队尾插入,在队头获取
int front = 0,tail = -1;
int main()
{
scanf("%d%d",&n,&k);
for(int i = 0;i<n;i++)
{
scanf("%d",&a[i]);
}
//先找出这个窗口的最小值
for(int i = 0;i < n;i++)
{
if(front <= tail && i - k + 1 > q[front])
front ++;
while(front <= tail && a[i] <= a[q[tail]] ) tail--;
//从队尾插入元素
q[++tail] = i;
//队头为窗口的最小值
if(i >= k-1) printf("%d ",a[q[front]]);
}
printf("\n");
//再找出这个窗口的最大值
front = 0,tail = -1;
for(int i = 0;i<n;i++)
{
if(front <= tail && i - k + 1 > q[front]) front++;
while(front <= tail && a[i] >= a[q[tail]]) tail--;
q[++tail] = i;
if(i >= k - 1) printf("%d ",a[q[front]]);
}
return 0;
}KMP算法
暴力算法怎么做?如何去优化?

#include<iostream>
using namespace std;
const int N = 100010,M = 1000010;
int n,m;
int ne[N];
char s[M],p[N];
int main()
{
cin >> n >> p + 1 >> m >> s + 1;
//查找next数组进行一个匹配
for(int i = 2,j = 0;i <= n;i++)
{
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j+1]) j++;
ne[i] = j;
}
//匹配操作
for(int i = 1,j = 0;i <= m;i++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] == p[j+1]) j++;
if(j == n)
{
printf("%d ",i - n);
//j = ne[j];
}
}
return 0;
}这两张图片参考的acwing的四谷夕雨的

