目录
1.排序
概念
排序就是让一串记录按照某个规定,递增或递减的排列起来的操作
稳定性:稳定性就是在排序前后 ,两个相同元素的下标前后关系保持不变,如 arr[ i ] ==arr [ j ] , i < j ,排序完成之后这两元素的下标还是前面的小于后面的 , 就称为稳定排序,否则就是不稳定排序
如果出现大范围排序,跳跃交换元素,一般就是不稳定排序
内部排序:数据元素全部放在内存中的排序
外部排序 :数据元素太多不能放在内存中,根据排序过程的要求不断的在内外存之间移动数据的排序
内存和外存(硬盘)的区别
1.内存的访问速度比硬盘(外存)快
2.内存的存储空间比硬盘(外存)小
3.内存上的数据断电后就消失了
硬盘的数据断电后还在,能持久的存储数据
常见的排序算法

2.常见排序算法实现
(1)插入排序
直接插入排序
类似于往顺序表中间位置插入元素
该排序是稳定排序
排序方式:
给定一个数组,把这个数组分为两个区间
1.有序区间(已排序区间)
2.无序区间(待排序区间)
初始情况下,该数组是未经排序的,此时认为有序区间是空区间,无序区间是整个数组
每次选择无序区间的一个元素,就把这个元素插入到有序区间的合适位置上(如果前一个比待插入元素大,就交换两元素位置,没有则停止),有序区间扩大一位,无序区间缩小一位,直到无序区间大小为0
时间复杂度:O(N2)
空间复杂度:O(1)
实现:
java
//实现插入排序
private static void insertSort(int[] arr){
//每次取出循环的第一个元素插入有序区间
//整个循环N-1次
//bound就是边界,分出有序和无序区间
//有序区间[0,bound)
//无序区间[bound,arr.length)
for (int bound=1;bound<arr.length;bound++){
int val=arr[bound];
int cur=bound-1;
for (;cur>=0;cur--){
if(arr[cur]>val){//如果前面元素比后面大,把前面元素搬运到后面
arr[cur+1]=arr[cur];
}else break;//找到了要插入的位置,此时cur减了1
}
arr[cur+1]=val;//完成插入
}
}测试一下:
java
public static void main(String[] args) {
int[] arr={9,5,2,7};
insertSort(arr);
System.out.println(Arrays.toString(arr));
}
希尔排序(缩小增量排序)
时间复杂度:O(log n)
最坏情况下:O(N2) => 平均复杂度:O (N1.5)
空间复杂度:O(1)
稳定性:不稳定排序
排序原理:分组进行插入排序
1.先把整个数组分成若干组,在针对每一组分别进行插入排序
引入了gap(间隙)的概念
假设gap为3,每隔三个就是一个组的元素(下图相同下标颜色即为一个组)
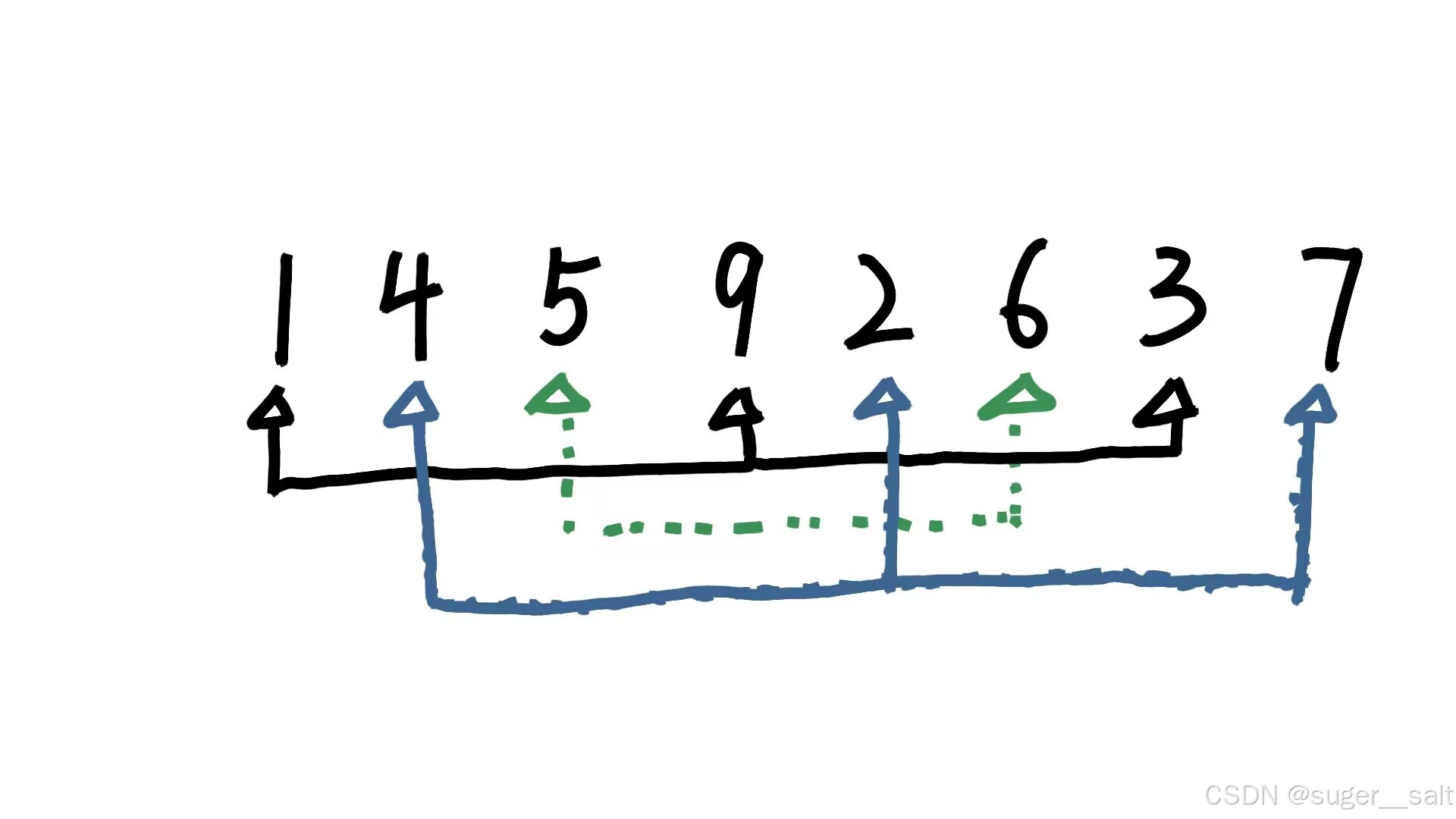
希尔排序不是值进行一次,而是要进行若干次的
插排完成后,依次把 gap 设置更小,直到变成 1 为止
希尔排序的好处:
普通的插入排序:
1.如果要排序的数组很短,整体效率就高
2.如果排序的数组基本有序了,整体效率也很高
希尔排序就结合了普通插入排序的两个优势 , Gap值大时组长度小,Gap值小时数组相对有序,因此效率更高
实现:
java
//分组进行插入排序
//根据gap值把整个数组分成多个组,针对每个组进行插入排序
//此处把gap设为 size/2, size/4 ,size/8....1
public static void shellSort(int[] arr){
int gap=arr.length/2;
while (gap>=1){
insertShellSort(arr,gap);//分组插排
gap/=2;//逐渐把gap值缩小
}
}
public static void insertShellSort(int[] arr,int gap){
for (int bound=gap;bound<arr.length;bound++){//针对每个组第1,2,3.。个元素排序
int val=arr[bound];
int cur=bound-gap;
for (;cur>=0;cur-=gap){//分别对组排序
if(arr[cur]>val){
arr[cur+gap]=arr[cur];//后移元素(为插入元素挪位置)
}else break;//找到了
}
arr[cur+gap]=val;
}
}测试:
java
public static void main(String[] args) {
int[] arr={9,5,2,7};
//insertSort(arr);
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
虽然希尔排序效率比普通插入排序高,但还是比不上后面的一些排序算法
(2)选择排序
直接选择排序
时间复杂度:O(N2)
空间复杂度:O(1)
稳定性:不稳定排序
原理:
把整个数组划分成两个部分,前面是有序区间,后面是无序区间
初始情况下,有序区间是空区间
从无序区间中找到最小值 (打擂台,以待排序区间的第一个元素位置作为"擂台",拿后续每个元素都和擂台的元素比较,如果比擂台元素小就交换),把这个值放到 无序区间的第一个位置
再把无序区间的第一个元素划分到有序区间,重复上述过程直到无序区间长度为0
实现:
java
//直接选择排序
public static void selectSort(int[] arr){
//bound为边界,界定有序和无序区间
for(int bound=0;bound<arr.length-1;bound++){
for (int cur=bound+1;cur<arr.length;cur++){
//cur表示要打擂台的元素位置
if(arr[cur]<arr[bound]){//打擂台成功
int t=arr[cur];
arr[cur]=arr[bound];
arr[bound]=t;
}
}
}
}测试运行:

堆排序
时间复杂度:O(NlogN)
空间复杂度:O(1)
稳定性:不稳定排序
堆排序比直接选择排序效率更高,甚至比前面所有排序算法的时间复杂度都低
前面选择排序是已排序在前面,待排序在后面,而堆排序想法,是已排序在后面,待排序在前面
如果要升序排序,就要建立大堆,根据堆顶元素最大的性质,把最大元素放到最后再向下调整,循环往复,直到待排序区间为0
设父节点下标为 i ,左子树下标2i +1,右子树下标2i+2
因为堆的父子下标关系有一个前提,根节点下标是0,所以前半部分不能是已排序区间
堆排序基本思路 :
1.针对整个数组建立大堆 ,初始情况下整个去加都是待排序区间
2.把堆顶 (最大元素)和最后一个元素位置交换 ,无序区间右区间减少一位
3.进行一次向下调整 ,重回大堆状态
4.重复上述过程,直到无序区间为0
实现:
java
public static void heapSort(int[] arr){
createHeap(arr);
for (int bound=arr.length-1;bound>=0;bound--){
int t=arr[0];
arr[0]=arr[bound];
arr[bound]=t;
shiftDown(arr,bound,0);
}
}
public static void shiftDown(int[] arr,int length,int index){
int parent=index;
int child=2*parent+1;
while (child<length){
if(child+1<length && arr[child+1]>arr[child]){
child++;
}
if(arr[child]>arr[parent]){
int t=arr[child];
arr[child]=arr[parent];
arr[parent]=t;
}else break;//调整完成
parent=child;
child=2*parent+1;
}
}
public static void createHeap(int[] arr){
for (int i=(arr.length-1-1)/2;i>=0;i--){
shiftDown(arr,arr.length,i);
}
}测试:

(3)交换排序
冒泡排序
时间复杂度:O(N2)
空间复杂度:O(1)
稳定性:稳定
原理:
比较交换相邻元素
一趟下来就能把最大值放到最后(或从后往前遍历,把最小值放到最前)
实现:
java
//从后往前遍历实现
public static void bubbleSort(int[] arr){
for (int i=0;i<arr.length-1;i++){
for (int j=arr.length-1;j>i;j--){
if(arr[j]<arr[j-1]){
int t=arr[j];
arr[j]=arr[j-1];
arr[j-1]=t;
}
}
}
}快速排序(hoare版)
时间复杂度:最坏情况 [ 待排序序列是反序的 ] 下是O(N2),平均时间复杂度是O(NlogN)
空间复杂度:最坏情况下是O(N),平均是O(logN) ---->因为递归会额外消耗空间
稳定性:不稳定排序
理解分治思想:即把一个大问题拆分成许多个小问题,然后慢慢解决小问题,从而将大问题解决
分治最理想的情况:分出来的左右区间长度差不多
快速排序思想 (这里选择最右侧为基准值):
给定一个待排序数组,从数组中选择一个 " 基准值 "
拿着数组中的每个元素和基准值比较,把该数组分 成三个部分
左侧:比基准值小的元素
中间:基准值
右侧:比基准值大的元素
然后对左右侧递归 ,重复上述过程(取基准值,分区间),直到区间只有三个或两个元素,排序完成
.
基准值分数组步骤 :1.选定数组最右侧元素为基准值,记录最左侧下标 i 和最右侧下标 j
2.先从左侧找 比基准值大 的元素(没找到则 i++),再从右侧下标找 比基准值小 的元素(没找到则 j - - )
第二步会出现两种情况
<1> 左右两侧都找到了元素 ,就交换两下标位置的元素,然后继续重复第二步
<2> 两下标位置重合,证明找完了(此时因为先从左侧找比基准值大的元素,所以该下标位置元素的值一定比基准值大),把基准值和该下标元素交换
快速排序的基准值也可以选最左侧元素作为基准值 ,此时要调整思路:
要先从右往左找 比基准值小的元素,再从左往右找比基准值大的元素
选取区间最右侧元素作为基准值,代码实现:
java
//快速查找,设置基准值为最右侧元素
private static void quickSort(int[] arr){
quickSort(arr,0,arr.length-1);
}
//规定区间为[left,right]
private static void quickSort(int[] arr,int left,int right){//实现递归
if(left>=right) return;
int index=partition(arr, left, right);//对区间进行调整,返回调整后基准值下标实现递归
quickSort(arr,left,index-1);//对左区间递归调整
quickSort(arr,index+1,right);//对右区间递归调整
}
private static int partition(int[] arr,int left,int right){
int l=left;
int r=right;
while (l<r){
while (l<r && arr[right]>arr[l]){//先从左往右找比基准值大的元素
l++;
}
while (l<r && arr[r]>arr[right]){
r--;
}
//两边都找到了,进行交换(就算下标重合交换也没事)
swap(arr,l,r);
}
//最后交换基准值和重合位置元素
swap(arr,l,right);
return l;//返回基准值下标位置
}
private static void swap(int[] arr,int left,int right){//交换两元素
int t=arr[left];
arr[left]=arr[right];
arr[right]=t;
}测试:

快速排序优化
1.为了避免反序效率低的极端情况,使用"三数取中" 的策略,即取出数组最左侧,最右侧,中间位置元素,比较三个数的大小,取中间值,再把这个中间值移到 最左侧 / 最右侧,方便后续交换操作
2.当递归到一定程度,每个区间比较小的时候,继续递归依然会消耗很多空间
此时在区间比较小的时候用插入排序速度更快
3.如果是特别大的数组,当地贵到一定深度时,此时区间长度还是比较大,可以使用堆排序对区间进行调整,而非继续递归
快速排序(非递归实现)
思路和上面快速排序一样,只是递归改为用栈模拟实现
java
static class Range{//保存左右区间
int left;
int right;
public Range(int left, int right) {
this.left = left;
this.right = right;
}
}
private static void quickSortByStack(int[] arr){
Stack<Range> stack=new Stack<>();
stack.push(new Range(0,arr.length-1));
while (!stack.isEmpty()){
Range range=stack.pop();
if(range.left>=range.right){
continue;
}
int index=partition(arr,range.left,range.right);
stack.push(new Range(range.left,index-1));//向左区间调整
stack.push(new Range(index+1,range.right));//向右区间调整
}
}
private static int partition(int[] arr,int left,int right){//就是之前的partitiong方法
int l=left;
int r=right;
while (l<r){
while (l<r && arr[right]>arr[l]){//先从左往右找比基准值大的元素
l++;
}
while (l<r && arr[r]>arr[right]){
r--;
}
//两边都找到了,进行交换(就算下标重合交换也没事)
swap(arr,l,r);
}
//最后交换基准值和重合位置元素
swap(arr,l,right);
return l;//返回基准值下标位置
}(4)归并排序
时间复杂度:O(NlogN)------>和logN相关
空间复杂度:O(N)
递归的空间复杂度:O(logN) ------->分区间是均匀的
由于合并数组要创建临时数组,所以整体复杂度为O(N)
稳定性:稳定排序
它也体现了分治思想
思路:
先把一个无序的数组拆分,如:
假设数组长度为N,先把这些数组对半拆,一直拆到每个区间长度为1,即只有一个元素
再两两合并数组,此时就是有序的数组了,一直合并直到整个区间长度为N
模拟实现:
java
private static void mergeSort(int[] arr){
mergeSort(arr,0,arr.length-1);//递归分区间
}
private static void mergeSort(int[] arr,int left,int right){//递归取得区间
if(left>=right) return;
int mid=(left+right)/2;//取得要分开的下标
mergeSort(arr,left,mid);//左半区间递归
mergeSort(arr,mid+1,right);//右半区间递归
//递归完了,对两个区间进行调整
merge(arr,left,mid,right);//合并区间
}
private static void merge(int[] arr,int left,int mid,int right){
int[] newArr=new int[right-left+1];
int resultSize=0;//记录位置
int cur1=left;
int cur2=mid+1;
while (cur1<=mid && cur2<=right){//模拟顺序表合并
if(arr[cur1]<=arr[cur2]){//稳定性取决于这个,两者相等取左边
newArr[resultSize++]=arr[cur1];
cur1++;
}else{
newArr[resultSize++]=arr[cur2];
cur2++;
}
}
while (cur1<=mid)
newArr[resultSize++]=arr[cur1++];
while (cur2<=right)
newArr[resultSize++]=arr[cur2++];
for(int i=0;i<resultSize;i++){//把临时数组的元素放到原数组中
arr[left+i]=newArr[i];
}
}归并排序与快速排序比较
1.快速排序:平均效率高,但是可能会出现极端情况,使得效率变低(发挥不稳定,忽高忽低)
2.归并排序:平均效率高,而且不存在极端最坏情况(发挥很稳定)
两者相较,归并排序更优
非递归版本的归并排序
时间复杂度和空间复杂度与前面的一致
思路:
数组从小区间开始合并,然后区间长度逐渐增大
实现:
java
//非递归版本归并排序
private static void mergeSortByLoop(int[] arr){
for(int size=1;size<arr.length;size*=2){//数组区间长度
for(int i=0;i<arr.length;i+=size*2){//对每个小区间合并
//左区间[i,i+size] 右区间[i+size+1,i+size*2-1]
int left=i;
int mid=i+size;
if(mid>arr.length-1){//避免超出范围
mid=arr.length-1;
}
int right=i+size*2-1;
if(right>arr.length-1){//避免超出范围
right=arr.length-1;
}
merge(arr,left,mid,right);
}
}
}
private static void merge(int[] arr,int left,int mid,int right){//和上面的的方法是一样的
int[] newArr=new int[right-left+1];
int resultSize=0;//记录位置
int cur1=left;
int cur2=mid+1;
while (cur1<=mid && cur2<=right){//模拟顺序表合并
if(arr[cur1]<=arr[cur2]){
newArr[resultSize++]=arr[cur1];
cur1++;
}else{
newArr[resultSize++]=arr[cur2];
cur2++;
}
}
while (cur1<=mid)
newArr[resultSize++]=arr[cur1++];
while (cur2<=right)
newArr[resultSize++]=arr[cur2++];
for(int i=0;i<resultSize;i++){//把临时数组的元素放到原数组中
arr[left+i]=newArr[i];
}
}归并排序的好处
1.归并排序是可以针对链表进行排序 的
堆排序/快速排序 (依赖下标)虽然效率都很高,但是只能针对数组,不能针对链表
归并排序是链表的高效排序的做法
2.归并排序,对于海量数据 (数据太多,内存无法同时保存下),也是能够处理 的
其他排序都要求所有数据必须同时在内存中才可以进行
例如有1000G的数据要排序,归并排序会先把1000GB拆分成1000个1GB,分别对1GB排序,再把这些数据合并
上述排序算法中,实用的排序
堆排序,快速排序,归并排序