【排队论】Probabilistic Forecasts of Bike-Sharing Systems for Journey Planning

abstract

我们研究了对共享单车系统（BSS）车站未来自行车可用性进行预测的问题。这是相关的，以便提出建议，保证用户能够进行旅行的概率足够高。为此，我们使用从BSS的排队理论时间非均匀模型中获得的概率预测。该模型已参数化，并使用巴黎市V'elib'BSS的历史数据成功验证。

我们对共享单车研究中常用的标准均方根误差（RMSE）进行了批判，将其作为预测准确性的指标，因为它没有考虑到真实系统中固有的随机性。相反，我们引入了一种基于评分规则的新指标。我们将模型的平均得分与文献中使用的经典预测因子进行比较。我们证明，在长达几个小时的预测范围内，我们的模型的表现优于这些模型。我们还讨论了，一般来说，测量当前可用自行车的数量仅适用于长达几个小时的预测范围。

一、要点

核心问题:如何预测共享单车站点未来自行车的可用性?

目标: 为用户提供高概率的行程可行性建议。

方法: 基于排队理论的时间非齐次模型。

数据验证:使用巴黎Vlib'系统的历史数据进行模型参数化和验证。

1.1 传统预测方法的局限性：RMSE的困局

传统方法采用RMSE（预测值和实际值的均方误差）进行评估，其在共享单车系统中具有局限性。忽略了系统的随机性（不可能完全准确，且永远不能为0），无法满足用户需求（无法表明用户是否借到车），RMSE具有下界。

传统指标:均方根误差(RMSE)广泛用于评估预测精度,
根本缺陷:RMSE未能充分考虑共享单车系统的固有随机性。这样导致预测误差不可避免。
理想情况下的RMSE:即使拥有完美信息，RMSE也无法达到零。经过案例研究，不同参数设置下，最佳预测器的RMSE仍然较高。
用户需求与RMSE脱节:用户更关心"能否成功骑行"，而非精确的自行车数量。

1.2 概率预测的优势：超越点估计

概率预测:预测未来自行车数量的概率分布，而非单一数值。
用户价值:直接提供用户关心的信息，如"出发站有自行车的概率"
系统优化:帮助运营商识别高风险站点，优化调度。
更全面的信息:提供更丰富的决策依据，例如平均值、方差等。

预测某个站点在半个小时后有车的概率是85%，对用户来说告诉成功的可能性有多大，对于运行商来说可识别哪些站点更容易出现空战或者满战的情况，从而进行更精准的调度。

二、数学模型

具体模型设计待补充

三、排队论模型：共享单车站点的数学建模

3.1 模型特点

核心思想：将共享单车站点建模为一个排队论系统。站点的两个过程--取车和还车--不是匀速的且是随机的；用时间非齐次性泊松过程的数学模型来描述；到达过程、离去过程都服从泊松过程。

时间非齐次性：充分考虑一天内不同时间段用户行为的差异（例如，早晚高峰到达和离开的速率肯定不一致）
泊松过程假设：简化模型，便于参数估计和分析
站点独立假设：简化分析，适用于大规模BSS网络（现实中站点之间会相互影响，但在站点数量足够多的情况下，这个假设盒里，且被一些理论和实证研究支持。）

模型的亮点在于抓住共享单车系统随机性的特点，还能预测出未来某个时间点站内的有多少车的概率是多少。

3.2 模型参数

例如，每15分钟一段，统计每段内多少车被取走，又有多少车被还回来。

参数估计:使用Vlib'系统历史数据估计到达率和离开率。
分段常数假设: 将一天划分为多个时间窗口，假设在每个窗口内速率恒定

3.3 模型验证

模型验证:验证到达和离开过程是否符合泊松分布。
K-S检验:使用Kolmogorov-Smirnov检验评估数据与泊松分布的拟合程度。
结果表明，大部分站点的数据确实比较接近泊松分布，验证了假设是靠谱的。

四、概率评分规则：评估概率预测的新标准

4.1 评分规则

即不去预测未来某一个确定的值，而去预测未来某个时间点，站点有X辆车的概率是多少。

衡量判断预测能否帮助用户判断是否成功借到车。

评分规则:用于评估概率预测准确性的度量标准。
Proper Scoring Rule:鼓励预测者诚实报告真实概率分布。
常用评分规则:Brier score, Spherical score, Logarithmic score.
用户中心评分规则:设计新的评分规则，直接评估行程可行性预测。

4.2 新定义的规则：用户中心评分规则

用户需求:用户更关心"是否有自行车可用"，而非具体数量。
阈值策略:用户根据预测概率p和阈值 p ∗ p^* p∗、决定是否前往站点。
评分规则设计:基于用户效用函数(衡量用户满意度)，设计新的评分规则，

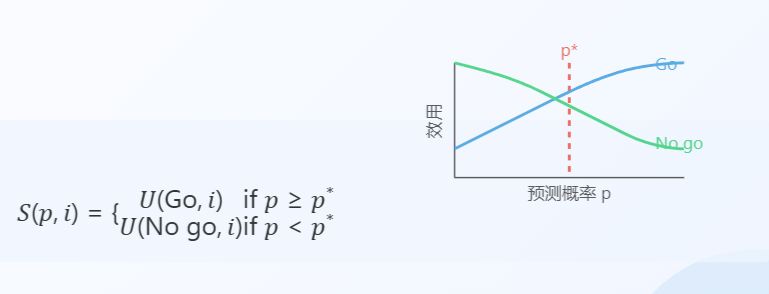
用户有一个效用函数，用于衡量用户满意度。比如，成功借到车的效用高于没借到车的效用，用户会根据预测的概率p和一个自己设定的阈值 p ∗ p^* p∗来决定是否去站点。如果预测概率大于等于阈值，就去;否则不去。评分规则是根据用户最终的决策结果和实际发生的情况来打分。

理解：用户会预测去完站点i有车的概率为p=85%，若大于其阈值 p ∗ p^* p∗=80% ，执行Go.去了之后能不能借到车是一个新的效用函数。因为现实情况是可能借到车,也可能借不到。

用户因为预测做出了正确的决策，得分就高；反之，则低。

这样可以直接评估模型在帮助用户决策方面的表现。

五、实验结果：概率预测模型的优越性

使用巴黎Vib'的真实数据，比较了我们提出的排队模型(QMP),历史预测模型(HP)和最后值预测模型(LVP)三种方法在不同评分规则下的表现。

预测时长：5min-10h不等

主要发现：

QMP模型在中短预测(2-5h)中表现最佳
HP模型在长期预测中略有优势
LVP模型在所有预测时长中表现最差

六错误决策概率分析：阈值策略下的模型表现

显然有不同的预测模型p以及不同的阈值p*,那么如何选择正确的模型和阈值是关键的。所以研究者分析了不同预测模型在不同的阈值下，导致错误决策的概率。结果发现，QMP模型表现更好，无论用户设定的阈值是高还是低，它导致错误决策的概率都相对较低。所以QMP模型不仅预测的准，而且能够更好的指导用户的实际决策。

七、结论和展望

结论

基于排队论的BSS站点可用性预测模型有效
概率预测和评分规则评估方法更贴合实际需求
QMP模型在中短期预测中优于传统方法

展望

考虑站点间的相关影响，构建更精细的网络模型
验证模型在其他BSS数据上的泛化能力
探索更复杂的用户行为和环境因素对预测的影响。