📝前言:
这篇文章我们来讲讲红黑树,本文章在有AVL树的基础上进行讲解。
🎬个人简介:努力学习ing
📋个人专栏:C++学习笔记
🎀CSDN主页 愚润求学
🌄其他专栏:C语言入门基础,python入门基础,python刷题专栏,Linux
文章目录
- 一,复习AVL的旋转操作
- 二,红黑树的特性
-
- [1 主要特性](#1 主要特性)
- [2 算法效率](#2 算法效率)
- 三,红黑树的调整方法
一,复习AVL的旋转操作
AVL树要求,左右子树高度差不超过1,当超过 1 的时候就要进行旋转操作。
旋转操作又分为单旋和双旋,当父亲和孩子同侧高时用单旋,异侧高时用双旋。
下面以右单选和左右双旋为例。(左右双旋其实也是两次单旋,孩子先左单选,变成同侧高,然后再对父亲右单旋)
当父亲A和孩子B同为左边高时(如图2),需要对A进行右单旋
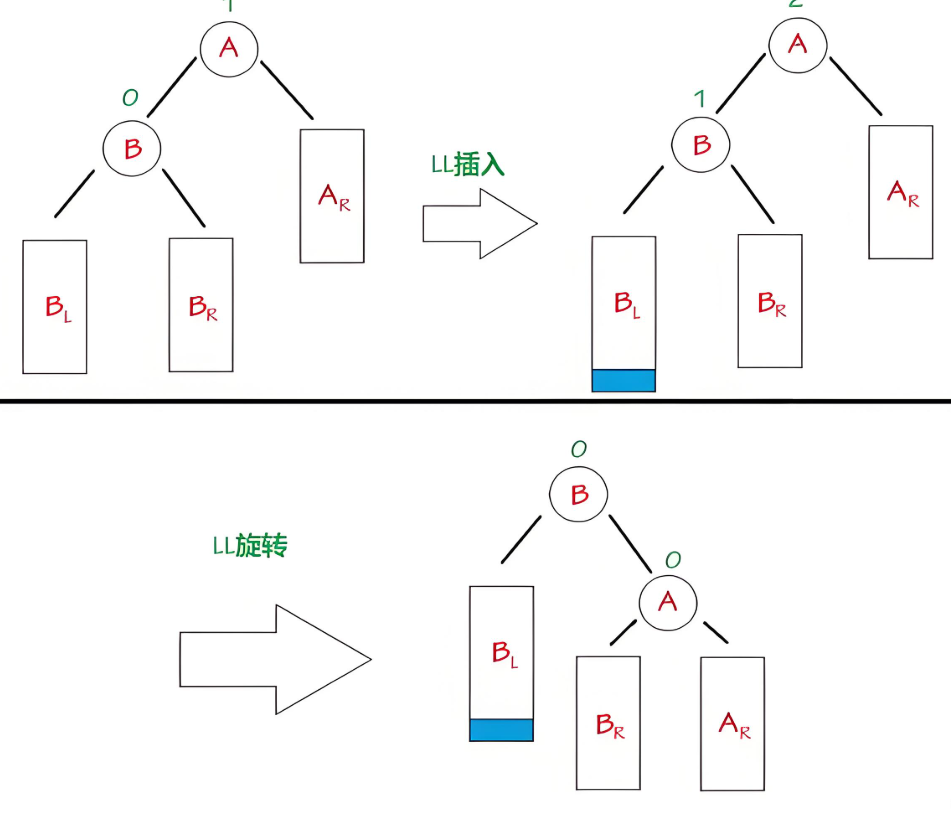
右单旋关键步骤:
- 把B的右孩子
BR给 A 的左边 - 然后把A压下来,当做B的右孩子
当下面这种情况就要进行双旋:

我们把插入后的BR展开,更好看两次单旋的过程拆分
先对孩子B进行左单旋,再对父亲A进行右单旋

这里的平衡因子结果只是在一开始插入后,C的平衡因子为零的结果。其他插入情况需要具体情况具体分析,如果不嫌弃可以看我的笔记:

二,红黑树的特性
红黑树是⼀棵⼆叉搜索树,他的每个结点增加⼀个存储位来表示结点的颜色,可以是红色或者黑色。通过对任何⼀条从根到叶子的路径上各个结点的颜色进行约束,红黑树确保没有⼀条路径会比其他路径长出2倍,因而是接近平衡的。
1 主要特性
主要的四大特性:
1. 每个节点不是红色就是黑色
2. 根节点是黑色
3. 红色节点的两个孩子必须是黑色
4. 对于任意一个节点,从该节点到其所有NULL结点的简单路径上,均包含相同数量的黑色结点(注意看路径的时候要数到空节点)
有些书上把这些空节点叫做NIL并且认为它们是黑色的
如:

通过规则2,3,4我们可以很容易求证:红黑树确保没有⼀条路径会比其他路径长出2倍。因为,最短路径情况:全是黑。最长路径情况:一黑一红。
2 算法效率
因为最长路径不会大于最短路径的两倍,而最短路径的最后一个节点所在层往上是一颗完全二叉树(因为要满足路径上有相同个数的黑色节点),所以,就算最长路径为最短路径的两倍,高度也不过:2*log(N)(N为节点个数),查找时间复杂度还是O(log(N))

(可见上图,节点10以上是一颗满二叉树,最长路径到达的节点50,深度只是节点10对应的满二叉树的两倍)
虽然查找的效率上可能比不过AVL树,但是因为红黑树对"平衡"的要求更宽松,所以,在调整操作的次数上,比AVL树少的多。
三,红黑树的调整方法
红黑树和AVL树大致相同,不过红黑树不利用平衡因子来标识是否平衡,而是通过节点的颜色来进行判断。
什么是调整
所谓调整平衡就是:每插入一个节点时,都通过调整,重新让红黑树满足前面提到的4大特性,使其依然是红黑树。
首先,我们思考一个问题:新插入的节点应该是什么颜色?
答案:必须是红色。
因为,插入黑色必然会导致当前路径上的黑色节点数量和其他路径不同了。(插入都是找找到NULL位置插入的,别忘了)
那插入时,什么时候需要调整呢?
答案:当插入的节点的父亲节点是红色时才需要调整!(此时出现了连红,父亲孩子都是红色)
当父亲为黑色时,插入后,依然满足4大特性,不需要调整
调整又分为下面4不同的场景:
在具体了解之前,我们先来理解一下下面这幅图:

如果我们把father节点的父亲叫做grandfather,cur代表我们插入的节点。
则,当插入红色节点后,三个节点的颜色是一定的:cur:红色,father:红色,grandfather:黑色(因为father原来是红色,grandfather原来只能是黑色)
这时候只有uncle不确定(uncle是唯一变量,也是我们采取不同调整策略的决定因素)
场景一:U为红
场景:

(当然F也可以是G的右孩子,C也可以是F的右孩子,这里只是示例)
你也可以暂停,先自己想一想怎么调整。
方法:仅变色
- F变黑(无论什么场景下F都要变黑,因为F不能和C连红)
- G变红
- U变黑
具体流程图:

我们可以想想为什么这样变?
- F必须要变黑,解决了连红 ,但是导致左侧这一路多了1个黑
- G变红,所有经过G的路径少一个黑,解决了1带来的问题,但是导致U这一路也少了一个黑
- U变黑,补回来一个黑
G变红了,但是,G的父节点(图中空白的节点)也是红呢?那就要把G当C继续向上调整。
【也就是说,其实C可以不仅代表一个节点,也可以代表一颗树(这可太关键了) ,因为如果代表一颗树,C原来是grandfather,为黑色。从grandfather这个节点往下,肯定也是一颗红黑树。】
你要问我为什么?因为满足四大特性,回头去看吧!
场景二:U不存在
此时C一定是新增的。
因为如果不是新增的,代表原来为下面子树的根节点grandfather变上来的,原来是黑色,但是这显然不可能,因为违反了特性,如图:

路径1比路径2少一个黑节点
场景:

方法(变色+单旋):
- F变黑,
- G变红,
- 单旋转
为什么要单旋?
F变黑,多一个黑。G变红,减了一个黑,原来从G节点右孩子NULL出的路径也少了一个黑(所以,可见,当一个黑节点作为路径终点的时候,无法轻易改变颜色)
具体流程 :

因为此时,F为黑,这时候无须再往上调整。
场景三:U为黑色,GFC成直线
这个场景下,C一定是原来的grandfather变来的。(不过多解释了,画图易知)

方法(变色+单旋):
- F变黑
- G变红
- 单旋
思路和场景二一样,为什么单旋,原因也一样,就不解释了。

这样操作以后也无须再向上更新,F的右孩子也不用担心和G连红,右孩子的根节点肯定是黑,因为本来F就是红
场景四:GFC不成直线,U为黑色或不存在
同样,U不存在,则C⼀定是新增结点,U存在且为⿊,则C⼀定不是新增

方法(变色+双旋)【我更喜欢记作:单旋 + (变色 + 单旋)(场景三)】:
- C 变黑
- G 变红
- 双旋
为什么变的是C和G?
我们先做一次单旋:

这就是场景三(只不过C与F换了位置,这就是变C颜色的原因),记住双旋多做一次旋就是为了转换成单旋的场景
具体流程:

调整方法总结
- U为红:仅变色(FGU)
- U不存在:变色(FG) + 单旋
- U为黑色,GFC成直线:变色(FG) + 单旋
- GFC不成直线,U为黑色或不存在:变色(CG)+ 双旋【单旋 + 变色(CG) + 单旋】
🌈我的分享也就到此结束啦🌈
要是我的分享也能对你的学习起到帮助,那简直是太酷啦!
若有不足,还请大家多多指正,我们一起学习交流!
📢公主,王子:点赞👍→收藏⭐→关注🔍
感谢大家的观看和支持!祝大家都能得偿所愿,天天开心!!!