弗洛伊德算法（Floyd）

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

介绍

弗洛伊德算法（Floyd算法）是一种用于解决图中任意两点之间的最短路径的算法。它是一种动态规划算法，由罗伯特·弗洛伊德（Robert Floyd）于1962年提出。弗洛伊德算法的基本思想是通过中间节点的递归遍历，逐步更新图中任意两点之间的最短路径。弗洛伊德算法的时间复杂度为O(n^3)，适用于解决稠密图中任意两点之间的最短路径问题。

弗洛伊德算法的应用领域非常广泛，包括网络路由算法、图像处理、自动化规划等。在网络路由算法中，弗洛伊德算法常用于计算路由表，以确定网络中任意两点之间的最短路径。在图像处理中，弗洛伊德算法常用于图像分割、图像匹配等领域。在自动化规划中，弗洛伊德算法常用于路径规划、机器人导航等应用。

弗洛伊德算法的核心思想是动态规划。在计算任意两点之间的最短路径时，弗洛伊德算法通过递归遍历中间节点，逐步更新最短路径。具体步骤如下：

初始化：将图中任意两点之间的距离初始化为无穷大，将图中任意两点之间的直接距离初始化为它们之间的距离。将中间节点初始化为无穷大。
递归更新：遍历图中的所有节点，以每个节点为中间节点，更新任意两点之间的最短路径。具体步骤如下：
- 对于每一对节点i、j，以节点k为中间节点，更新节点i、j之间的距离：如果节点i、j之间的距离大于节点i、k之间的距离加上节点k、j之间的距离，则更新节点i、j之间的距离为节点i、k之间的距离加上节点k、j之间的距离。
重复递归：重复步骤2，直到所有节点为中间节点的最短路径都被更新。
输出最短路径：最终得到任意两点之间的最短路径。

弗洛伊德算法的时间复杂度为O(n^3)，空间复杂度为O(n^2)，其中n为图中节点的个数。弗洛伊德算法的优点是能够解决任意两点之间的最短路径问题，适用于解决稠密图中的最短路径问题。弗洛伊德算法的缺点是时间复杂度较高，对于大规模图的计算较为耗时。

总之，弗洛伊德算法是一种用于解决图中任意两点之间的最短路径的动态规划算法。它的核心思想是通过递归遍历中间节点，逐步更新最短路径。弗洛伊德算法在网络路由算法、图像处理、自动化规划等领域有广泛的应用。弗洛伊德算法的时间复杂度为O(n^3)，适用于解决稠密图中的最短路径问题。弗洛伊德算法是图算法中的重要算法之一，对于解决图中的最短路径问题具有重要的意义。

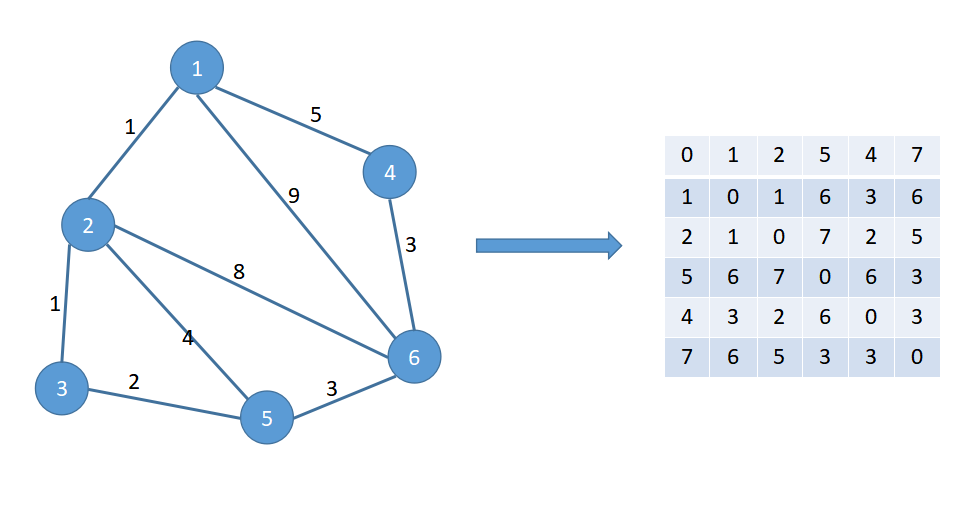
1. 弗洛伊德算法的基本思想

弗洛伊德算法的基本思想是动态规划。在计算任意两点之间的最短路径时，算法通过递归遍历中间节点，逐步更新最短路径。算法的核心在于利用中间节点的递归思想，通过动态规划的方式逐步优化路径长度，最终得到图中所有节点之间的最短路径。

2. 弗洛伊德算法的核心步骤

弗洛伊德算法的核心步骤包括初始化和递归更新两个阶段：

2.1 初始化阶段

将图中任意两点之间的距离初始化为无穷大，将图中任意两点之间的直接距离初始化为它们之间的距离。
将中间节点的距离初始化为无穷大。

2.2 递归更新阶段

遍历图中的所有节点，以每个节点为中间节点，更新任意两点之间的最短路径。
对于每一对节点i、j，以节点k为中间节点，更新节点i、j之间的距离：如果节点i、j之间的距离大于节点i、k之间的距离加上节点k、j之间的距离，则更新节点i、j之间的距离为节点i、k之间的距离加上节点k、j之间的距离。

2.3 重复递归阶段

重复递归更新阶段，直到所有节点为中间节点的最短路径都被更新。

2.4 输出最短路径

最终得到图中所有节点之间的最短路径。

3. 弗洛伊德算法的时间复杂度

弗洛伊德算法的时间复杂度为O(n^3)，其中n为图中节点的个数。算法中的三重循环是导致时间复杂度较高的原因，因此在大规模图的计算中，算法可能会耗费较长时间。

4. 弗洛伊德算法的优点和缺点

4.1 优点：

能够解决任意两点之间的最短路径问题，适用于解决稠密图中的最短路径问题。
算法思想简单，易于理解和实现。

4.2 缺点：

时间复杂度较高，对于大规模图的计算可能会耗费较长时间。
空间复杂度较高，需要维护大量的中间节点距离信息。

5. 弗洛伊德算法的应用

弗洛伊德算法在网络路由算法、图像处理、自动化规划等领域有广泛的应用。在网络路由算法中，弗洛伊德算法常用于计算路由表，以确定网络中任意两点之间的最短路径。在图像处理中，弗洛伊德算法常用于图像分割、图像匹配等领域。在自动化规划中，弗洛伊德算法常用于路径规划、机器人导航等应用。

6. 总结

弗洛伊德算法是一种经典的动态规划算法，用于解决图中任意两点之间的最短路径问题。算法通过递归遍历中间节点，逐步更新最短路径，最终得到图中所有节点之间的最短路径。弗洛伊德算法的时间复杂度为O(n^3)，适用于解决稠密图中的最短路径问题。算法在网络路由算法、图像处理、自动化规划等领域有广泛的应用，是图算法中的重要算法之一。弗洛伊德算法的优点是能够解决任意两点之间的最短路径问题，易于理解和实现，但缺点是时间复杂度较高，对于大规模图的计算可能会耗费较长时间。

算法实现

弗洛伊德算法（Floyd算法）是一种经典的动态规划算法，用于解决图中任意两点之间的最短路径问题。该算法的实现涉及到图的表示、距离矩阵的初始化、动态规划的递归更新等步骤。在本节中，我们将详细介绍弗洛伊德算法的实现过程，包括算法的伪代码、代码实现、时间复杂度分析等内容。

1. 弗洛伊德算法的伪代码

下面是弗洛伊德算法的伪代码实现：

```

procedure FloydWarshall (graph)

let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)

let next be a |V| × |V| array of vertex indices initialized to NULL

for each edge (u, v) in graph

dist[u][v] = graph[u][v]

next[u][v] = v

for each vertex v in graph

dist[v][v] = 0

next[v][v] = v

for k from 1 to |V|

for i from 1 to |V|

for j from 1 to |V|

if dist[i][j] > dist[i][k] + dist[k][j]

dist[i][j] = dist[i][k] + dist[k][j]

next[i][j] = next[i][k]

```

2. 弗洛伊德算法的代码实现（Python示例）

下面是弗洛伊德算法的Python代码实现示例：

```python

def floyd_warshall(graph):

dist = [[float('inf') for _ in range(len(graph))] for _ in range(len(graph))]

next = [[None for _ in range(len(graph))] for _ in range(len(graph))]

for u in range(len(graph)):

for v in range(len(graph)):

dist[u][v] = graph[u][v]

next[u][v] = v

for v in range(len(graph)):

dist[v][v] = 0

next[v][v] = v

for k in range(len(graph)):

for i in range(len(graph)):

for j in range(len(graph)):

if dist[i][j] > dist[i][k] + dist[k][j]:

dist[i][j] = dist[i][k] + dist[k][j]

next[i][j] = next[i][k]

return dist, next

```

3. 弗洛伊德算法的时间复杂度分析

弗洛伊德算法的时间复杂度为O(n^3)，其中n为图中节点的个数。算法中的三重循环是导致时间复杂度较高的原因。在实际应用中，算法的时间复杂度可能在处理大规模图的情况下导致较长的计算时间。

4. 弗洛伊德算法的应用示例

下面是一个简单的示例，展示如何使用弗洛伊德算法计算图中任意两点之间的最短路径：

```python

graph = [

0, 3, 8, float('inf')\], \[float('inf'), 0, 2, 4\], \[float('inf'), float('inf'), 0, 1\], \[float('inf'), float('inf'), float('inf'), 0

]

distances, next_vertices = floyd_warshall(graph)

print("Shortest distances between each pair of vertices:")

for i in range(len(graph)):

for j in range(len(graph)):

if distances[i][j] == float('inf'):

print(f"Distance from vertex {i} to vertex {j} is infinity")

else:

print(f"Distance from vertex {i} to vertex {j} is {distances[i][j]}")

```

5. 总结

弗洛伊德算法是一种经典的动态规划算法，用于解决图中任意两点之间的最短路径问题。算法的实现涉及到图的表示、距离矩阵的初始化、动态规划的递归更新等步骤。通过递归更新中间节点，算法能够高效地计算图中任意两点之间的最短路径。弗洛伊德算法在网络路由算法、图像处理、自动化规划等领域有广泛的应用，是图算法中的重要算法之一。

整体代码

cpp 复制代码

#include <iostream>
#include <vector>
#include <climits>

using namespace std;

const int INF = 1e9; // 定义无穷大

int main() {
    int n, m;
    cin >> n >> m;

    // 初始化距离矩阵
    vector<vector<int>> dist(n + 1, vector<int>(n + 1, INF));

    // 自身到自身的距离为0
    for (int i = 1; i <= n; ++i) {
        dist[i][i] = 0;
    }

    // 读取边并处理重边
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        if (w < dist[u][v]) {
            dist[u][v] = w;
            dist[v][u] = w;
        }
    }

    // Floyd-Warshall算法
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (dist[i][k] != INF && dist[k][j] != INF) {
                    dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
                }
            }
        }
    }

    // 输出结果
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (dist[i][j] == INF) {
                cout << "0 "; // 根据题目描述，边权都是正整数，所以不可达的情况可能不存在，但按题意输出0
            } else {
                cout << dist[i][j] << " ";
            }
        }
        cout << endl;
    }

    return 0;
}

例题