一、正则化
1.1、正则化
正则化是一种用于控制模型复杂度的技术。它通过在损失函数中添加额外的项(正则 化项)来降低模型的复杂度,以防止过拟合。
在机器学习中,模型的目标是在训练数据上获得较好的拟合效果。然而,过于复杂的 模型可能会在训练数据上表现良好,但在未见过的数据上表现较差,这种现象称为过 拟合。为了避免过拟合,正则化技术被引入。

1.2、为什么加入正则化可以解决过拟合?
加入正则化之后,想要损失函数尽可能的小,不仅仅要让原来的MSE的 值尽可能的小,还需要让后面正则化项的值尽可能的小。 要让正则化项的的值尽可能的小,那么就要使的参数 尽可能的小。
参数 小和解决过拟合的关系:
过拟合的实质是模型过于复杂或者训练样本较少,也可以理解为:针对当前 样本,模型过于复杂。 模型的复杂程度是由参数的个数和参数大小范围决定的,那么如果降低参数 的大 小范围,就可以降低模型的复杂度,因此可以用来解决过拟合问题。
1.3、正则化的基本思想
正则化的基本思想是在损失函数中引入一个额外的项,该项与模型的复杂度相关。这 个额外的项可以是参数的平方和(L2正则化),参数的绝对值和(L1正则化)或其 他形式的复杂度度量。通过调整正则化参数,可以控制正则化项在损失函数中的权 重。
正则化的目的是通过在损失函数中添加一个正则项(通常是权重的 L1 或 L2 范 数),以惩罚模型的复杂度,从而避免过拟合问题。
1.4、L1正则化和L2正则化


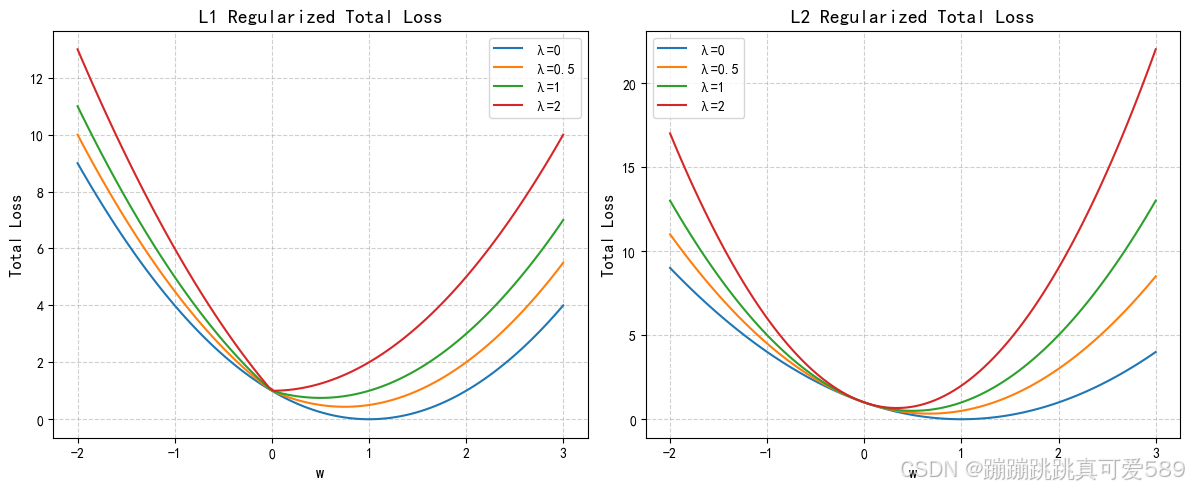
| 特性 | L1正则化 | L2正则化 |
|---|---|---|
| 稀疏性 | 产生稀疏解(部分权重为零) | 不产生稀疏解(权重接近零) |
| 优化特性 | 在零点不可导,需特殊处理 | 在零点可导,优化稳定 |
| 几何形状(2D) | 菱形 | 圆形 |
| 应用场景 | 特征选择、高维稀疏数据 | 防止过拟合、平滑权重分布 |
二、Dropout
Dropout是一种在神经网络训练过程中使用的正则化技术,旨在减少过拟合现象。其 思想是在每次训练迭代中,随机地将一部分神经元的输出置为0,即将其"丢弃",从 而降低神经网络对特定神经元的依赖性,减少神经网络的复杂度,增强神经网络的泛 化能力。

python
import torch
# 创建一个Dropout层,丢弃概率为0.2
m = torch.nn.Dropout(p=0.2)
# 生成一个形状为(10, 1)的随机输入张量
input = torch.randn(10, 1)
print("输入张量:")
print(input)
# 将Dropout层应用于输入张量
output = m(input)
print("应用Dropout后的输出:")
print(output)
def dropout_layer(X, dropout):
# 确保dropout概率在0和1之间
assert 0 <= dropout <= 1
# 如果dropout为1,返回与X形状相同的全零张量
if dropout == 1:
return torch.zeros_like(X)
# 如果dropout为0,返回原始张量X
if dropout == 0:
return X
# 创建一个掩码,其中值大于指定的dropout概率
mask = (X > dropout).float()
print("掩码张量:")
print(mask)
# 通过掩码调整输出,并按dropout概率进行缩放
return mask * X / (1.0 - dropout)
# 将自定义dropout层应用于输入张量
out = dropout_layer(input, 0.2)
print("自定义dropout层的输出:")
print(out) Dropout为什么能够解决过拟合:
(1)减少过拟合: 在标准的神经网络中,网络可能会过度依赖于一些特定的神经 元,导致对训练数据的过拟合。Dropout通过随机丢弃神经元,迫使网络学习对于任 何单个神经元的变化都要更加鲁棒的特征表示,从而减少了对训练数据的过度拟合。
(2)取平均的作用: 在训练过程中,通过丢弃随机的神经元,每次前向传播都相当 于在训练不同的子网络。在测试阶段,不再进行Dropout,但是通过保留所有的权 重,网络结构变得更加完整。因此,可以看作是在多个不同的子网络中进行了训练, 最终的预测结果相当于对这些子网络的输出取平均。这种"综合取平均"的策略有助于 减轻过拟合,因为一些互为反向的拟合会相互抵消。
三、设计思路

输入数据
python
class1_points = np.array(
[[-0.7, 0.7], [3.9, 1.5], [1.7, 2.2], [1.9, -2.4], [0.9, 1.4], [4.2, 0.9], [1.7, 0.7], [0.2, -0.2], [3.1, -0.4],
[-0.2, -0.9], [1.7, 0.2], [-0.6, -3.9], [-1.8, -4.0], [0.7, 3.8], [-0.7, -3.3], [0.8, 1.8], [-0.5, 1.5],
[-0.6, -3.6], [-3.1, -3.0], [2.1, -2.5], [-2.5, -3.4], [-2.6, -0.8], [-0.2, 0.9], [-3.0, 3.3], [-0.7, 0.2],
[0.3, 3.0], [0.6, 1.9], [-4.0, 2.4], [1.9, -2.2], [1.0, 0.3], [-0.9, -0.7], [-3.7, 0.6], [-2.7, -1.5], [0.9, -0.3],
[0.8, -0.2], [-0.4, -4.4], [-0.3, 0.8], [4.1, 1.0], [-2.5, -3.5], [-0.8, 0.3], [0.6, 0.6], [2.6, -1.0], [1.8, 0.4],
[1.5, -1.0], [3.2, 1.1], [3.3, -2.5], [-3.8, 2.5], [3.1, -0.9], [3.4, -1.1], [0.3, 0.8], [-0.1, 2.9], [-2.8, 1.9],
[2.8, -3.3], [-1.0, 3.1], [-0.8, -0.6], [-2.5, -1.5], [0.3, 0.2], [-1.0, -2.9], [0.7, 0.2], [-0.5, 0.9],
[-0.8, 0.7], [4.1, 0.5], [2.8, 2.3], [-3.9, 0.1], [2.2, -1.4], [-0.7, -3.5], [1.0, 1.2], [-0.7, -4.0], [1.3, 0.6],
[-0.1, 3.3], [0.0, -0.3], [1.8, -3.0], [0.6, 0.0], [3.6, -2.8], [-3.9, -0.9], [-4.3, -0.9], [0.1, -0.8],
[-1.6, -2.7], [-1.8, -3.3], [1.7, -3.5], [3.6, -3.1], [-2.4, 2.5], [-1.0, 1.8], [3.9, 2.5], [-3.9, -1.3],
[3.4, 1.6], [-0.1, -0.6], [-3.7, -1.3], [-0.3, 3.4], [-3.7, -1.7], [4.0, 1.1], [3.4, 0.2], [0.1, -1.6],
[-1.2, -0.5], [2.4, 1.7], [-4.4, -0.5], [-0.2, -3.6], [-0.8, 0.4], [-1.5, -2.2], [3.9, 2.5], [4.4, 1.4],
[-3.5, -1.1], [-0.7, 1.5], [-3.0, -2.6], [0.2, -3.5], [0.0, 1.2], [-4.3, 0.1], [-1.8, 2.8], [1.1, -2.5],
[0.2, 4.3], [-3.9, 2.2], [1.0, 1.6], [4.5, 0.2], [3.9, -1.6], [-0.4, -0.5], [0.3, -0.4], [-3.2, 1.7], [2.0, 4.1],
[2.5, 2.2], [-1.1, -0.3], [-3.7, -1.9], [1.5, -1.1], [-2.1, -1.9], [-0.1, 4.5], [3.8, -0.3], [-0.9, -3.8],
[-2.9, -1.6], [1.0, -1.2], [0.7, 0.0], [-0.8, 3.3], [-2.8, 3.1], [0.4, -3.2], [4.6, 1.0], [2.5, 3.1], [4.2, 0.8],
[3.6, 1.8], [1.4, -3.0], [-0.4, -1.4], [-4.1, 1.1], [1.1, -0.2], [-2.9, -0.0], [-3.5, 1.3], [-1.4, 0.0],
[-3.7, 2.2], [-2.9, 2.8], [1.7, 0.4], [-0.8, -0.6], [2.9, 1.1], [-2.3, 3.1], [-2.9, -2.0], [-2.7, -0.4],
[2.6, -2.4], [-1.7, -2.8], [1.2, 3.1], [3.8, 1.3], [0.1, 1.9], [-0.5, -1.0], [0.0, -0.5], [3.9, -0.7],
[-3.7, -2.5], [-3.1, 2.7], [-0.9, -1.0], [-0.7, -0.8], [-0.4, -0.1], [1.5, 1.0], [-2.6, 1.9], [-0.8, 1.7],
[0.8, 1.8], [2.0, 3.6], [3.2, 1.4], [2.3, 1.4], [4.9, 0.5], [2.2, 1.8], [-1.4, -2.7], [3.1, 1.1], [-1.0, 3.8],
[-0.4, -1.1], [3.3, 1.1], [2.2, -3.9], [1.0, 1.2], [2.6, 3.2], [-0.6, -3.0], [-1.9, -2.8], [1.2, -1.2],
[-0.4, -2.7], [1.1, -4.3], [0.3, -0.8], [-1.0, -0.4], [-1.1, -0.2], [0.1, 1.2], [0.9, 0.6], [-2.7, 1.6],
[1.0, -0.7], [0.3, -4.2], [-2.1, 3.2], [3.4, -1.2], [2.5, -4.0], [1.0, -0.8], [1.0, -0.9], [0.1, -0.6]])
class2_points = np.array(
[[-3.0, -3.8], [4.4, 2.5], [2.6, 4.1], [3.7, -2.7], [-3.7, -2.9], [5.3, 0.3], [3.9, 2.9], [-2.7, -4.5], [5.4, 0.2],
[3.0, 4.8], [-4.2, -1.3], [-2.1, -5.4], [-3.2, -4.6], [0.7, 4.5], [-1.4, -5.7], [0.5, 5.9], [-2.1, 4.0],
[-0.1, -5.1], [-3.4, -4.7], [3.3, -4.7], [-2.7, -4.1], [-4.5, -2.0], [4.3, 2.9], [-3.6, 4.0], [-0.5, 5.5],
[0.2, 5.2], [5.3, -0.9], [-4.5, 3.6], [3.4, -2.8], [-3.4, -3.7], [1.6, -5.5], [-5.9, -0.1], [-4.8, -2.5],
[-5.5, 0.3], [1.6, 4.4], [-0.9, -5.3], [-1.0, 5.4], [4.9, 0.8], [-3.1, -4.0], [2.3, 4.7], [4.0, -1.6], [4.9, -1.5],
[4.2, -2.5], [-3.5, 3.7], [4.7, 0.5], [5.3, -2.6], [-5.0, 2.4], [5.5, -1.2], [5.6, -1.3], [3.3, -4.3], [-1.3, 4.4],
[-4.1, 3.6], [3.3, -4.5], [-2.3, 5.2], [2.6, 4.6], [-4.4, -1.6], [4.7, -2.0], [-1.7, -4.9], [-5.1, -2.4],
[4.5, 3.2], [-3.9, -3.4], [6.0, -0.4], [3.5, 4.3], [-4.9, -0.6], [3.3, -3.2], [-0.3, -4.8], [-1.6, -4.7],
[-1.4, -4.6], [-3.1, 3.8], [-1.4, 4.9], [1.8, -4.5], [2.2, -5.5], [3.1, -3.4], [4.7, -2.8], [-5.3, -0.4],
[-6.0, -0.1], [1.4, -4.5], [-3.1, -4.3], [-1.8, -5.7], [1.7, -5.6], [4.5, -3.7], [-2.6, 4.3], [-3.4, 3.4],
[4.7, 3.1], [-5.2, -2.8], [5.4, 1.2], [-5.4, 1.2], [-4.9, -1.3], [-1.3, 5.6], [-4.1, -2.6], [5.0, 1.0], [5.2, 1.2],
[2.4, -4.9], [-3.2, 3.8], [3.3, 3.4], [-5.5, -0.8], [0.6, -5.0], [1.2, 5.4], [-3.4, -3.3], [4.6, 2.8], [5.2, 1.7],
[-4.4, -0.9], [-5.0, -1.3], [-3.1, -3.6], [-0.7, -4.5], [5.9, -0.9], [-5.1, -0.5], [-2.6, 5.2], [1.4, -4.8],
[-0.7, 5.6], [-5.3, 2.1], [4.9, 2.6], [5.3, 0.9], [5.1, -1.2], [2.7, -4.4], [-2.0, -5.6], [-4.9, 3.2], [2.8, 5.3],
[2.6, 3.9], [-0.0, 5.7], [-5.7, -1.8], [-1.1, -4.7], [-2.4, -3.8], [-1.1, 5.6], [5.3, -1.5], [-0.4, -5.8],
[-4.5, -1.6], [-4.4, -3.7], [-4.3, 2.4], [0.1, 4.8], [-3.0, 3.8], [0.3, -5.8], [5.6, 0.5], [4.1, 3.6], [5.0, 1.5],
[5.7, 1.5], [3.2, -4.1], [-1.7, -5.6], [-5.3, 0.9], [4.3, 3.0], [-5.4, 0.3], [-5.0, 0.8], [2.7, 5.1], [-5.0, 2.2],
[-4.0, 3.0], [-4.4, -3.9], [-3.5, -3.9], [5.3, 1.5], [-4.2, 4.2], [-3.9, -4.0], [-4.7, -0.1], [3.7, -4.7],
[-3.0, -4.7], [2.7, 4.4], [4.3, 2.0], [-3.6, -4.5], [5.5, 0.9], [-4.7, -2.8], [5.5, -2.2], [-5.1, -2.6],
[-3.6, 3.1], [-3.2, -4.0], [-4.8, 1.3], [-5.5, -1.6], [4.1, -1.6], [-4.2, 3.6], [5.6, -1.4], [4.9, -3.3],
[1.7, 4.9], [5.3, 2.5], [3.8, 2.8], [5.8, 0.7], [3.9, 2.6], [-2.1, -4.8], [5.2, 2.5], [-2.0, 4.3], [2.8, -4.1],
[5.6, 0.8], [2.2, -5.2], [-1.1, 5.5], [4.2, 3.8], [-1.8, -5.2], [-3.4, -3.6], [3.7, -3.6], [-0.5, -4.8],
[1.9, -5.6], [-1.1, 5.4], [2.3, 4.7], [0.0, -5.4], [2.1, -5.6], [4.8, -0.3], [-4.7, 2.9], [-3.8, 3.9], [0.9, -5.5],
[-2.3, 3.6], [5.3, -2.5], [3.7, -4.6], [-5.0, 2.4], [0.0, -5.7], [0.2, -5.9]])
# 合并两类点
points = np.concatenate((class1_points, class2_points))
# 标签 0表示类别1,1表示类别2
labels1 = np.zeros(len(class1_points))
labels2 = np.ones(len(class2_points))
labels = np.concatenate((labels1, labels2))构建模型
python
class ModelClass(nn.Module):
def __init__(self):
super().__init__()
# 定义网络层结构:
self.layer1 = nn.Linear(2, 16) # 输入层(2维特征)→ 16维隐藏层
self.layer2 = nn.Linear(16, 48) # 16维 → 48维隐藏层
self.layer3 = nn.Linear(48, 32) # 48维 → 32维隐藏层
self.layer4 = nn.Linear(32, 2) # 32维 → 输出层(2类概率)
# 定义Dropout层(随机丢弃神经元防止过拟合)
self.dropout1 = nn.Dropout(p=0.1) # 丢弃概率10%
self.dropout2 = nn.Dropout(p=0.1)
self.dropout3 = nn.Dropout(p=0.1)
def forward(self, x):
x = torch.relu(self.layer1(x)) # 第一层后接ReLU激活函数
x = self.dropout1(x) # 应用Dropout
x = torch.relu(self.layer2(x)) # 第二层 + ReLU
x = self.dropout2(x)
x = torch.relu(self.layer3(x)) # 第三层 + ReLU
x = self.dropout3(x)
x=self.layer4(x) # 输出层Softmax获取概率
return x
# 初始化模型实例
model = ModelClass()构建损失函数和优化器
python
criterion = nn.CrossEntropyLoss() # 交叉熵损失函数(多分类任务常用)
optimizer = optim.Adam(model.parameters(), lr=0.01) # Adam优化器,学习率0.01训练模型
python
num_iterations = 2000 # 总迭代次数
batch_size = 32 # 批量大小
for n in range(num_iterations + 1):
model.train() # 设置模型为训练模式(启用Dropout)
# 分批训练
for batch_start in range(0, len(points), batch_size):
# 获取当前批次的数据和标签
batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size], dtype=torch.float32)
batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)
# 前向传播
outputs = model(batch_inputs)
loss = criterion(outputs, batch_labels) # 计算损失
# 反向传播与优化
optimizer.zero_grad() # 清空梯度缓存
loss.backward() # 反向传播计算梯度
optimizer.step() # 更新权重参数
# 每隔100次迭代可视化结果
if n % 100 == 0 or n == 1:
print(n,loss.item())可视化
python
num_iterations = 2000 # 总迭代次数
batch_size = 32 # 批量大小
for n in range(num_iterations + 1):
model.train() # 设置模型为训练模式(启用Dropout)
# 分批训练
for batch_start in range(0, len(points), batch_size):
# 获取当前批次的数据和标签
batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size], dtype=torch.float32)
batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)
# 前向传播
outputs = model(batch_inputs)
loss = criterion(outputs, batch_labels) # 计算损失
# 反向传播与优化
optimizer.zero_grad() # 清空梯度缓存
loss.backward() # 反向传播计算梯度
optimizer.step() # 更新权重参数
# 每隔100次迭代可视化结果
if n % 100 == 0 or n == 1:
print(n,loss.item())
model.eval() # 设置模型为评估模式(关闭Dropout)
with torch.no_grad(): # 关闭梯度计算
# 预测所有网格点的类别概率
grid_points_tensor = torch.tensor(grid_points, dtype=torch.float32)
Z = model(grid_points_tensor).numpy()
Z = Z[:, 1] # 获取类别2的概率值
# 调整形状以匹配网格矩阵
Z = Z.reshape(xx.shape)
# 绘制分类结果
plt.cla() # 清空当前图像
plt.scatter(class1_points[:, 0], class1_points[:, 1], c='blue', label='Class 1')
plt.scatter(class2_points[:, 0], class2_points[:, 1], c='red', label='Class 2')
plt.contour(xx, yy, Z, levels=[0.5], colors='black') # 绘制0.5概率等高线作为决策边界
plt.title(f"Epochs: {n}")
plt.show() # 显示最终图像完整代码
python
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# --------------------------------------------- 数据准备部分 ---------------------------------------------
# 类别1的二维坐标点(蓝色点)
class1_points = np.array(
[[-0.7, 0.7], [3.9, 1.5], [1.7, 2.2], [1.9, -2.4], [0.9, 1.4], [4.2, 0.9], [1.7, 0.7], [0.2, -0.2], [3.1, -0.4],
[-0.2, -0.9], [1.7, 0.2], [-0.6, -3.9], [-1.8, -4.0], [0.7, 3.8], [-0.7, -3.3], [0.8, 1.8], [-0.5, 1.5],
[-0.6, -3.6], [-3.1, -3.0], [2.1, -2.5], [-2.5, -3.4], [-2.6, -0.8], [-0.2, 0.9], [-3.0, 3.3], [-0.7, 0.2],
[0.3, 3.0], [0.6, 1.9], [-4.0, 2.4], [1.9, -2.2], [1.0, 0.3], [-0.9, -0.7], [-3.7, 0.6], [-2.7, -1.5], [0.9, -0.3],
[0.8, -0.2], [-0.4, -4.4], [-0.3, 0.8], [4.1, 1.0], [-2.5, -3.5], [-0.8, 0.3], [0.6, 0.6], [2.6, -1.0], [1.8, 0.4],
[1.5, -1.0], [3.2, 1.1], [3.3, -2.5], [-3.8, 2.5], [3.1, -0.9], [3.4, -1.1], [0.3, 0.8], [-0.1, 2.9], [-2.8, 1.9],
[2.8, -3.3], [-1.0, 3.1], [-0.8, -0.6], [-2.5, -1.5], [0.3, 0.2], [-1.0, -2.9], [0.7, 0.2], [-0.5, 0.9],
[-0.8, 0.7], [4.1, 0.5], [2.8, 2.3], [-3.9, 0.1], [2.2, -1.4], [-0.7, -3.5], [1.0, 1.2], [-0.7, -4.0], [1.3, 0.6],
[-0.1, 3.3], [0.0, -0.3], [1.8, -3.0], [0.6, 0.0], [3.6, -2.8], [-3.9, -0.9], [-4.3, -0.9], [0.1, -0.8],
[-1.6, -2.7], [-1.8, -3.3], [1.7, -3.5], [3.6, -3.1], [-2.4, 2.5], [-1.0, 1.8], [3.9, 2.5], [-3.9, -1.3],
[3.4, 1.6], [-0.1, -0.6], [-3.7, -1.3], [-0.3, 3.4], [-3.7, -1.7], [4.0, 1.1], [3.4, 0.2], [0.1, -1.6],
[-1.2, -0.5], [2.4, 1.7], [-4.4, -0.5], [-0.2, -3.6], [-0.8, 0.4], [-1.5, -2.2], [3.9, 2.5], [4.4, 1.4],
[-3.5, -1.1], [-0.7, 1.5], [-3.0, -2.6], [0.2, -3.5], [0.0, 1.2], [-4.3, 0.1], [-1.8, 2.8], [1.1, -2.5],
[0.2, 4.3], [-3.9, 2.2], [1.0, 1.6], [4.5, 0.2], [3.9, -1.6], [-0.4, -0.5], [0.3, -0.4], [-3.2, 1.7], [2.0, 4.1],
[2.5, 2.2], [-1.1, -0.3], [-3.7, -1.9], [1.5, -1.1], [-2.1, -1.9], [-0.1, 4.5], [3.8, -0.3], [-0.9, -3.8],
[-2.9, -1.6], [1.0, -1.2], [0.7, 0.0], [-0.8, 3.3], [-2.8, 3.1], [0.4, -3.2], [4.6, 1.0], [2.5, 3.1], [4.2, 0.8],
[3.6, 1.8], [1.4, -3.0], [-0.4, -1.4], [-4.1, 1.1], [1.1, -0.2], [-2.9, -0.0], [-3.5, 1.3], [-1.4, 0.0],
[-3.7, 2.2], [-2.9, 2.8], [1.7, 0.4], [-0.8, -0.6], [2.9, 1.1], [-2.3, 3.1], [-2.9, -2.0], [-2.7, -0.4],
[2.6, -2.4], [-1.7, -2.8], [1.2, 3.1], [3.8, 1.3], [0.1, 1.9], [-0.5, -1.0], [0.0, -0.5], [3.9, -0.7],
[-3.7, -2.5], [-3.1, 2.7], [-0.9, -1.0], [-0.7, -0.8], [-0.4, -0.1], [1.5, 1.0], [-2.6, 1.9], [-0.8, 1.7],
[0.8, 1.8], [2.0, 3.6], [3.2, 1.4], [2.3, 1.4], [4.9, 0.5], [2.2, 1.8], [-1.4, -2.7], [3.1, 1.1], [-1.0, 3.8],
[-0.4, -1.1], [3.3, 1.1], [2.2, -3.9], [1.0, 1.2], [2.6, 3.2], [-0.6, -3.0], [-1.9, -2.8], [1.2, -1.2],
[-0.4, -2.7], [1.1, -4.3], [0.3, -0.8], [-1.0, -0.4], [-1.1, -0.2], [0.1, 1.2], [0.9, 0.6], [-2.7, 1.6],
[1.0, -0.7], [0.3, -4.2], [-2.1, 3.2], [3.4, -1.2], [2.5, -4.0], [1.0, -0.8], [1.0, -0.9], [0.1, -0.6]])
class2_points = np.array(
[[-3.0, -3.8], [4.4, 2.5], [2.6, 4.1], [3.7, -2.7], [-3.7, -2.9], [5.3, 0.3], [3.9, 2.9], [-2.7, -4.5], [5.4, 0.2],
[3.0, 4.8], [-4.2, -1.3], [-2.1, -5.4], [-3.2, -4.6], [0.7, 4.5], [-1.4, -5.7], [0.5, 5.9], [-2.1, 4.0],
[-0.1, -5.1], [-3.4, -4.7], [3.3, -4.7], [-2.7, -4.1], [-4.5, -2.0], [4.3, 2.9], [-3.6, 4.0], [-0.5, 5.5],
[0.2, 5.2], [5.3, -0.9], [-4.5, 3.6], [3.4, -2.8], [-3.4, -3.7], [1.6, -5.5], [-5.9, -0.1], [-4.8, -2.5],
[-5.5, 0.3], [1.6, 4.4], [-0.9, -5.3], [-1.0, 5.4], [4.9, 0.8], [-3.1, -4.0], [2.3, 4.7], [4.0, -1.6], [4.9, -1.5],
[4.2, -2.5], [-3.5, 3.7], [4.7, 0.5], [5.3, -2.6], [-5.0, 2.4], [5.5, -1.2], [5.6, -1.3], [3.3, -4.3], [-1.3, 4.4],
[-4.1, 3.6], [3.3, -4.5], [-2.3, 5.2], [2.6, 4.6], [-4.4, -1.6], [4.7, -2.0], [-1.7, -4.9], [-5.1, -2.4],
[4.5, 3.2], [-3.9, -3.4], [6.0, -0.4], [3.5, 4.3], [-4.9, -0.6], [3.3, -3.2], [-0.3, -4.8], [-1.6, -4.7],
[-1.4, -4.6], [-3.1, 3.8], [-1.4, 4.9], [1.8, -4.5], [2.2, -5.5], [3.1, -3.4], [4.7, -2.8], [-5.3, -0.4],
[-6.0, -0.1], [1.4, -4.5], [-3.1, -4.3], [-1.8, -5.7], [1.7, -5.6], [4.5, -3.7], [-2.6, 4.3], [-3.4, 3.4],
[4.7, 3.1], [-5.2, -2.8], [5.4, 1.2], [-5.4, 1.2], [-4.9, -1.3], [-1.3, 5.6], [-4.1, -2.6], [5.0, 1.0], [5.2, 1.2],
[2.4, -4.9], [-3.2, 3.8], [3.3, 3.4], [-5.5, -0.8], [0.6, -5.0], [1.2, 5.4], [-3.4, -3.3], [4.6, 2.8], [5.2, 1.7],
[-4.4, -0.9], [-5.0, -1.3], [-3.1, -3.6], [-0.7, -4.5], [5.9, -0.9], [-5.1, -0.5], [-2.6, 5.2], [1.4, -4.8],
[-0.7, 5.6], [-5.3, 2.1], [4.9, 2.6], [5.3, 0.9], [5.1, -1.2], [2.7, -4.4], [-2.0, -5.6], [-4.9, 3.2], [2.8, 5.3],
[2.6, 3.9], [-0.0, 5.7], [-5.7, -1.8], [-1.1, -4.7], [-2.4, -3.8], [-1.1, 5.6], [5.3, -1.5], [-0.4, -5.8],
[-4.5, -1.6], [-4.4, -3.7], [-4.3, 2.4], [0.1, 4.8], [-3.0, 3.8], [0.3, -5.8], [5.6, 0.5], [4.1, 3.6], [5.0, 1.5],
[5.7, 1.5], [3.2, -4.1], [-1.7, -5.6], [-5.3, 0.9], [4.3, 3.0], [-5.4, 0.3], [-5.0, 0.8], [2.7, 5.1], [-5.0, 2.2],
[-4.0, 3.0], [-4.4, -3.9], [-3.5, -3.9], [5.3, 1.5], [-4.2, 4.2], [-3.9, -4.0], [-4.7, -0.1], [3.7, -4.7],
[-3.0, -4.7], [2.7, 4.4], [4.3, 2.0], [-3.6, -4.5], [5.5, 0.9], [-4.7, -2.8], [5.5, -2.2], [-5.1, -2.6],
[-3.6, 3.1], [-3.2, -4.0], [-4.8, 1.3], [-5.5, -1.6], [4.1, -1.6], [-4.2, 3.6], [5.6, -1.4], [4.9, -3.3],
[1.7, 4.9], [5.3, 2.5], [3.8, 2.8], [5.8, 0.7], [3.9, 2.6], [-2.1, -4.8], [5.2, 2.5], [-2.0, 4.3], [2.8, -4.1],
[5.6, 0.8], [2.2, -5.2], [-1.1, 5.5], [4.2, 3.8], [-1.8, -5.2], [-3.4, -3.6], [3.7, -3.6], [-0.5, -4.8],
[1.9, -5.6], [-1.1, 5.4], [2.3, 4.7], [0.0, -5.4], [2.1, -5.6], [4.8, -0.3], [-4.7, 2.9], [-3.8, 3.9], [0.9, -5.5],
[-2.3, 3.6], [5.3, -2.5], [3.7, -4.6], [-5.0, 2.4], [0.0, -5.7], [0.2, -5.9]])
# 合并两类点
points = np.concatenate((class1_points, class2_points))
# 标签 0表示类别1,1表示类别2
labels1 = np.zeros(len(class1_points))
labels2 = np.ones(len(class2_points))
labels = np.concatenate((labels1, labels2))
# --------------------------------------------- 模型定义部分 ---------------------------------------------
class ModelClass(nn.Module):
def __init__(self):
super().__init__()
# 定义网络层结构:
self.layer1 = nn.Linear(2, 16) # 输入层(2维特征)→ 16维隐藏层
self.layer2 = nn.Linear(16, 48) # 16维 → 48维隐藏层
self.layer3 = nn.Linear(48, 32) # 48维 → 32维隐藏层
self.layer4 = nn.Linear(32, 2) # 32维 → 输出层(2类概率)
# 定义Dropout层(随机丢弃神经元防止过拟合)
self.dropout1 = nn.Dropout(p=0.1) # 丢弃概率10%
self.dropout2 = nn.Dropout(p=0.1)
self.dropout3 = nn.Dropout(p=0.1)
def forward(self, x):
x = torch.relu(self.layer1(x)) # 第一层后接ReLU激活函数
x = self.dropout1(x) # 应用Dropout
x = torch.relu(self.layer2(x)) # 第二层 + ReLU
x = self.dropout2(x)
x = torch.relu(self.layer3(x)) # 第三层 + ReLU
x = self.dropout3(x)
x=self.layer4(x) # 输出层Softmax获取概率
return x
# 初始化模型实例
model = ModelClass()
# --------------------------------------------- 训练配置部分 ---------------------------------------------
criterion = nn.CrossEntropyLoss() # 交叉熵损失函数(多分类任务常用)
optimizer = optim.Adam(model.parameters(), lr=0.01) # Adam优化器,学习率0.01
# 生成网格点用于绘制决策边界
x_min, x_max = points[:, 0].min() - 1, points[:, 0].max() + 1
y_min, y_max = points[:, 1].min() - 1, points[:, 1].max() + 1
step_size = 0.1
xx, yy = np.meshgrid(np.arange(x_min, x_max, step_size),
np.arange(y_min, y_max, step_size))
grid_points = np.c_[xx.ravel(), yy.ravel()] # 生成网格坐标矩阵
# --------------------------------------------- 训练循环部分 ---------------------------------------------
num_iterations = 2000 # 总迭代次数
batch_size = 32 # 批量大小
for n in range(num_iterations + 1):
model.train() # 设置模型为训练模式(启用Dropout)
# 分批训练
for batch_start in range(0, len(points), batch_size):
# 获取当前批次的数据和标签
batch_inputs = torch.tensor(points[batch_start:batch_start + batch_size], dtype=torch.float32)
batch_labels = torch.tensor(labels[batch_start:batch_start + batch_size], dtype=torch.long)
# 前向传播
outputs = model(batch_inputs)
loss = criterion(outputs, batch_labels) # 计算损失
# 反向传播与优化
optimizer.zero_grad() # 清空梯度缓存
loss.backward() # 反向传播计算梯度
optimizer.step() # 更新权重参数
# 每隔100次迭代可视化结果
if n % 100 == 0 or n == 1:
print(n,loss.item())
model.eval() # 设置模型为评估模式(关闭Dropout)
with torch.no_grad(): # 关闭梯度计算
# 预测所有网格点的类别概率
grid_points_tensor = torch.tensor(grid_points, dtype=torch.float32)
Z = model(grid_points_tensor).numpy()
Z = Z[:, 1] # 获取类别2的概率值
# 调整形状以匹配网格矩阵
Z = Z.reshape(xx.shape)
# 绘制分类结果
plt.cla() # 清空当前图像
plt.scatter(class1_points[:, 0], class1_points[:, 1], c='blue', label='Class 1')
plt.scatter(class2_points[:, 0], class2_points[:, 1], c='red', label='Class 2')
plt.contour(xx, yy, Z, levels=[0.5], colors='black') # 绘制0.5概率等高线作为决策边界
plt.title(f"Epochs: {n}")
plt.show() # 显示最终图像