实习 / 春秋招｜必知必会的 ACM 模式输入输出与构造

C++ ACM 模式输入输出

1. 输入输出的相关库函数

1️⃣ 输出格式化（精度）

C++ 提供了多种方式来控制输入输出的格式，常用的包括 std::setw、std::setprecision、std::fixed 等。

cpp 复制代码

#include <iostream>
#include <iomanip>  // 提供格式化工具

int main() {
    double pi = 3.14159265358979;
    
    std::cout << "原始值: " << pi << std::endl;

    // 设置输出精度为 2 位小数
    std::cout << "保留两位小数: " << std::fixed << std::setprecision(2) << pi << std::endl;
    return 0;
}

2️⃣ cin

cin 是标准输入流对象，通常用于从用户那里读取数据。当我们用 while (cin) 来读取输入时，它的工作原理是不断检查输入流是否有效。如果用户输入了数据并且没有遇到错误或者文件结束标志（例如 Ctrl+Z 或 Ctrl+D 表示 EOF），那么 cin 就会继续读取并进入循环。

注意，cin >> val 会一直从 标准输入流 中读取数据，以空白字符为分隔符，包括：

空格 ' '
回车 '\n'
制表符 '\t'

这些都是分隔符，但 不会终止输入流，只是划分输入的不同部分。

3️⃣ stringstream

std::stringstream 是 C++ 标准库中的一个类，位于 <sstream> 头文件中。它提供了一个用于在内存中进行输入输出操作的字符串流。std::stringstream 允许你像使用 std::cin 和 std::cout 一样操作字符串，它可以用来从字符串中读取数据，或将数据写入到字符串中。它的主要用途是进行字符串的格式化和数据的转换。

std::stringstream 继承自 std::iostream，因此可以使用 << 和 >> 运算符来进行数据流的输入输出。如果想清空 stringstream 中的数据，可以使用 str("") 方法，将流的内容设置为空字符串，或者使用 clear() 来重置流的状态。

cpp 复制代码

#include <iostream>
#include <sstream>

int main() {
    std::stringstream ss1;
    int x = 10;
    double y = 3.14;
    ss1 << "Integer: " << x << ", Double: " << y;
    std::cout << ss.str() << std::endl;
    
    std::stringstream ss2("123 456 3.14");
    int a, b;
    double c;
    ss >> a >> b >> c;
    std::cout << "a: " << a << ", b: " << b << ", c: " << c << std::endl;
    
    // 清空: ss.str("")
    ss1.str("");
}

4️⃣ getline

getline 函数是 C++ 中用于从输入流中读取一行文本的函数，通常用于读取用户输入或文件中的一行数据。它的基本用法是：读取一整行数据，直到遇到换行符（\n）为止。它不会将换行符包含在返回的字符串中。函数原型为：

cpp 复制代码

istream& getline (istream& is, string& str);

它接受两个参数：

is：输入流对象（如 cin 或 ifstream）。
str：存储读取内容的 string 对象。

cpp 复制代码

#include <iostream>
#include <string>
using namespace std;

int main() {
    // 输入 1 2 3 4
    string line;
    while (getline(cin, line)) {
        cout << "输入的行是: " << line << endl;
    }
    return 0;
}

cpp 复制代码

#include <iostream>
#include <string>
using namespace std;

int main() {
    std::string input;
    std::cin >> input;  // 输入 1,2,3,4

    std::stringstream ss(input);
    std::vector<int> nums;
    std::string number;
	// stringstream, string
    while (getline(ss, number, ',')) {
        nums.push_back(std::stoi(number));
    }
    return 0;
}

2. A+B+C+...（单行输入版）

输入样例：

复制代码

1 2 3 4 5

输出样例：

复制代码

题解：

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int main() {
  // 数据范围: -10^9 <= x <= 10^9
  long long val, s = 0;
  while (cin >> val) {
    s += val;
  }
  cout << s << endl;
  return 0;
}

3. A+B+C+...（多行输入版）

输入样例：

cpp 复制代码

1 2 3
4 5 6 7
8 9

输出样例：

cpp 复制代码

6
22
17

题解：

cpp 复制代码

#include <iostream>
#include <sstream>
using namespace std;

int main() {
  string line;
  while (getline(cin, line)) { // 持续读取完整一行，一直到 EOF
    // 使用 stringstream 解析每一行的输入
    // 假设读到的是"1 2 3"
    stringstream ss(line);
    long long num, sum = 0;
    while (ss >> num) { // 逐个读取这一行的整数
      sum += num;       // 将读取的整数累加到 sum 中
                        // 先是sum += 1
                        // 再是sum += 2
                        // 最后是sum += 3
    }
    cout << sum << endl; // 输出这一行所有整数的和 : 6
  }
  return 0;
}

🔥 4. A+B+C+...（带元素个数的多行输入版）

输入：

cpp 复制代码

输出：

cpp 复制代码

3
1
0

⚠️ 本题反而要注意：cin 不是读到 \n 停止，而是 EOF，所以 line 14 不能用 while(cin >> val) 来替代，否则后续元素都会被吸收到 nums 数组中。

cpp 复制代码

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int n, Q;
  cin >> n >> Q;

  vector<int> nums(n);
  for (int i = 0; i < n; i++) {
    cin >> nums[i];
  }
  vector<int> query(Q);
  for (int i = 0; i < Q; i++) {
    cin >> query[i];
  }
  return 0;
}

或者可以使用 cin.peek() != '\n' 搭配 cin >> val 使用（这一刻我才明白 cin.peek() 与 cin.ignore() 的作用）：

记得先处理上一行的末尾（如果需要处理）：cin.ignore() 或 cin.get()
再使用 cin.peek() != '\n' & cin >> val 来循环读取当前行元素

cpp 复制代码

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int n, Q;
  cin >> n >> Q;
  //vector<int> nums(n);
  //for (int i = 0; i < n; i++) {
  //  cin >> nums[i];
  //}
    
// 等价于
    
  // 🔥注意这里需要处理第一行的 '\n', 因为 cin >> n >> Q 后还没跳到下一行。
  cin.ignore();	// 或者 cin.get();
  vector<int> nums;
  int val;
  while (cin.peek() != '\n' && cin >> val) {
      nums.push_back(val);
  }
  vector<int> query(Q);
  for (int i = 0; i < Q; i++) {
    cin >> query[i];
  }
  return 0;
}

⚠️ 拓展延伸

1️⃣ 上述的输入是：

scss 复制代码

5 3⏎(换行)
1 2 2 3 2⏎(换行)
2⏎(换行)
3⏎(换行)
4⏎(换行)

2️⃣ 假设输入变成以下这种（即第二行换行符前还有一个␣(空格)）：

scss 复制代码

5 3⏎(换行)
1 2 2 3 2␣(空格)⏎(换行)
2⏎(换行)
3⏎(换行)
4⏎(换行)

那 nums 的个数会有 6 个，即第 3 行的 2 也会当成 nums 的元素，因为 ␣(空格) 不是 \n，所以会再触发一次 cin 操作，所以建议使用 for (int i = 0; i < n; i++) { cin >> nums[i]; } 的方式替代 peek() 判断！

OJ 时间复杂度限制与预估

在编写程序时，分析其时间复杂度（Time Complexity）是评估程序效率的重要手段。时间复杂度描述了程序运行时间与输入规模之间的关系，通常使用大O符号表示（如O(n)、O(n²)等）。下面将详细解释时间复杂度的概念，并分析这段代码的时间复杂度。

🔥 OJ 一般 C++ 1秒（即1000ms）大概能跑 1e8 量级（很多题目都会限制时间和内存，如下：

时间限制: C/C++ 1000ms , 其他语言： 2000ms

内存限制: C/C++ 256MB , 其他语言： 512MB

cpp 复制代码

#include <iostream>
using namespace std;
int x;
int ans = 0;
int main() {
	cin>>x;
	for (int i = 1; i <= x; i++) {
		ans++;
	}
	cout<<ans;
	return 0;
}

🔥对于这个简单的代码，x < 1e8 , 运行不会超时， x > 1e8 , 运行超时

✅ 时间复杂度衡量的是算法执行所需的时间增长率，随着输入规模的增加，算法的运行时间如何变化。常见的时间复杂度包括：

O(1)：常数时间，无论输入规模多大，执行时间保持不变。
O(log n)：对数时间，随着输入规模增加，执行时间按对数增长。例如二分操作。
O(n)：线性时间，执行时间与输入规模成正比。
O(n log n)：线性对数时间，常见于高效排序算法如快速排序、归并排序。
O(n²)：平方时间，常见于简单的嵌套循环，如冒泡排序。

✅ 如何计算时间复杂度：

识别基本操作：确定算法中最频繁执行的操作，如循环中的语句、递归调用等。
计算基本操作的执行次数：根据输入规模，计算这些操作随着输入增长的次数。
忽略低阶项和常数系数：在大O表示法中，只保留增长最快的项，忽略常数和低阶项。

🔥 对于一般情况：

n= <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 0 5 10^5 </math>105 或 n= <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 0 6 10^6 </math>106 左右考虑 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n l o g n ) O(n log n) </math>O(nlogn) 以下的做法
n= <math xmlns="http://www.w3.org/1998/Math/MathML"> 5 ∗ 1 0 3 5 * 10^3 </math>5∗103 左右考虑 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2) 以下的做法
n= <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 0 2 10^2 </math>102 左右考虑 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 3 ) O(n^3) </math>O(n3) 以下的做法
n= <math xmlns="http://www.w3.org/1998/Math/MathML"> 20 20 </math>20 左右考虑 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( 2 n ) O(2^n) </math>O(2n) 以下的做法

各数据类型的读入与构造

数组

cpp 复制代码

#include <bits/stdc++.h>
#include <numeric>
using namespace std;

int main() {
  int n;
  cin >> n;
  vector<int> nums(n);
  for (int i = 0; i < n; i++) {
    cin >> nums[i];
  }
  cout << accumulate(nums.begin(), nums.end(), 0) << endl;
  return 0;
}

链表

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

struct ListNode {
  int val;
  ListNode *next;
  ListNode(int x) : val(x), next(nullptr) {}
};

ListNode *createLinkedList(vector<int> &nums) {
  ListNode dummy(0);
  ListNode *cur = &dummy;
  for (int x : nums) {
    cur->next = new ListNode(x);
    cur = cur->next;
  }
  return dummy.next;
}

void printLinkedList(ListNode *head) {
  for (ListNode *cur = head; cur; cur = cur->next) {
    cout << cur->val << endl;
  }
}

int main() {
  int n;
  cin >> n; // 读取数组长度

  vector<int> nums(n);
  for (int i = 0; i < n; i++) {
    cin >> nums[i]; // 读取数组元素
  }

  ListNode *head = createLinkedList(nums); // 创建链表
  printLinkedList(head);                   // 遍历链表并输出

  return 0;
}

二叉树的读入与构建（输入为数组形式）

本题相当于根据「层序遍历」结果来构造二叉树：本质就是根据数组索引来构造

✅ 推荐阅读（题解）：

输入

cpp 复制代码

1 2 3 4 5 -1 6

树的结构

cpp 复制代码

输出

cpp 复制代码

题解

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

TreeNode *buildTree(const vector<int> &nums) {
  if (nums.empty() || nums[0] == -1)
    return nullptr;
  vector<TreeNode *> nodes(nums.size(), nullptr);
  for (size_t i = 0; i < nums.size(); i++) {
    if (nums[i] != -1)
      nodes[i] = new TreeNode(nums[i]);
  }
  for (size_t i = 0; i < nums.size(); i++) {
    if (nodes[i]) {
      if (2 * i + 1 < nums.size())
        nodes[i]->left = nodes[2 * i + 1];
      if (2 * i + 2 < nums.size())
        nodes[i]->right = nodes[2 * i + 2];
    }
  }
  return nodes[0];
}

void levelOrder(TreeNode *root) {
  if (!root)
    return;
  queue<TreeNode *> q;
  q.push(root);
  while (!q.empty()) {
    TreeNode *curr = q.front();
    q.pop();
    cout << curr->val << endl;
    if (curr->left)
      q.push(curr->left);
    if (curr->right)
      q.push(curr->right);
  }
}

int main() {
  string line;
  getline(cin, line);
  stringstream ss(line);
  vector<int> nums;
  int val;
  while (ss >> val) {
    nums.push_back(val);
  }
  TreeNode *root = buildTree(nums);
  levelOrder(root);
  return 0;
}

普通树的读入与构建（输入为相邻边 & father 数组）

分成两种形式的读入，一起讲解

题目描述

给定一棵 n 个节点的树，节点编号为1−n1−n ，树的根节点固定为 1。我们有两种方式表示树的结构：

方式一 ：通过 n-1 条边的形式，每条边 u v 表示节点 u 和节点 v 之间存在一条边。
方式二 ：通过一个 father 数组，father[i] 表示节点 i+1 的父节点。

请你编写程序，读入树的结构并使用深度优先搜索遍历打印这棵树的节点编号。

为了输出统一，从根节点开始遍历，优先访问序号小的子节点。

输入

输入包含三部分：

第一行包含一个整数 n，表示树的节点个数。
第二行包含一个整数 type，表示树的表示方式：
- 如果 type = 1，表示通过边的形式输入。
- 如果 type = 2，表示通过 father 数组输入。
如果 type = 1，接下来会有 n-1 行，每行两个整数 u v，表示树中节点 u 和节点 v 之间存在一条边。
如果 type = 2，接下来一行有 n 个整数，father[i] 表示节点 i+1 的父节点，其中 father[0] = 0，表示 1 号节点为根节点,没有父节点。

输出

打印遍历这棵树的节点编号。

输入样例 1

cpp 复制代码

输出样例 1

cpp 复制代码

1 2 4 5 3

样例1 图例

cpp 复制代码

输入样例 2

cpp 复制代码

5
2
0 1 1 2 2

输出样例 2

cpp 复制代码

1 2 4 5 3

数据范围

<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 ≤ n ≤ 1 0 5 1\le n \le 10^5 </math>1≤n≤105

🔥题解

cpp 复制代码

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

#define MAX 100005 // 假设最大节点数 10^5

vector<int> adjList[MAX];    // 邻接表
vector<int> traversalResult; // 存储先序遍历结果

void DFS(int node, int parent) {
  traversalResult.push_back(node);
  for (auto &child : adjList[node]) {
    if (child != parent) {
      DFS(child, node);
    }
  }
}

int main() {
  int n, type;
  cin >> n >> type;

  if (type == 1) {
    // type 1: 通过边的形式读入
    for (int i = 0; i < n - 1; i++) {
      int u, v;
      cin >> u >> v;
      adjList[u].push_back(v);
      adjList[v].push_back(u);
    }
  } else if (type == 2) {
    // type 2: 通过 father 数组输入
    vector<int> father(n + 1);
    for (int i = 1; i <= n; i++) {
      cin >> father[i];
      if (father[i] != 0) {
        adjList[father[i]].push_back(i);
        adjList[i].push_back(father[i]);
      }
    }
  }
  // 为了保证遍历顺序的一致性，先对每个节点的子节点进行排序
  for (int i = 1; i <= n; i++) {
    sort(adjList[i].begin(), adjList[i].end());
  }

  DFS(1, 0);

  for (int i = 0; i < (int)traversalResult.size(); i++) {
    if (i > 0)
      cout << ' ';
    cout << traversalResult[i];
  }
  return 0;
}

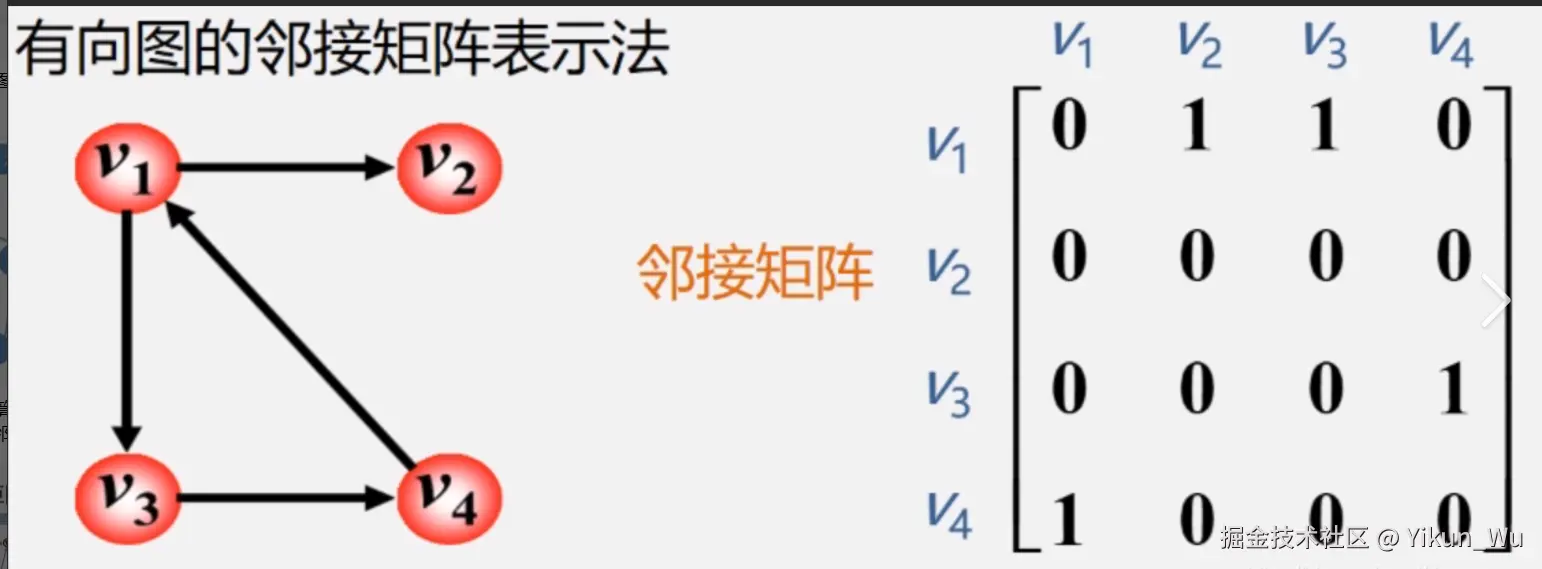
图的构造（邻接矩阵 & 邻接表）

题目描述

给定两张有向图 A 和 B，其中图 A 以邻接矩阵形式给出，图 B 以邻接表形式给出。请判断这两张图是否完全一样。我们将"完全一样"的定义为：每个节点的邻居集合完全一致。

输入

输入的第一行包含两个整数 n，表示图的节点数。

接下来的 n 行，给出图 A 的邻接矩阵。该矩阵的第 i 行第 j 列表示节点 i 和节点 j 之间是否有边。如果存在边，则该位置的值为 1，否则为 0。

接下来的 n 行，给出图 B 的邻接表。每行第一个数 node,后面跟的第一个数 k 表示接下来输入 k 个数 val 表示节点 node 向这些节点 val 连一条边。

输出

如果图 A 和图 B 完全一样，则输出 "YES"；否则输出 "NO"。

注意

图 A 和图 B 是有向图，即如果 A[i][j]=1，那么 i 到 j 有条有向边。
节点编号从 1 到 n。
图 A 和图 B 的节点数相同。
数据范围：
- <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 ≤ n ≤ 1 0 3 1≤n≤10^3 </math>1≤n≤103
- 图 A 的邻接矩阵大小为 n×n，其中每个元素为 0 或 1。
- 图 B 的邻接表中每个节点的邻居数量不超过 n−1。

样例输入 1

cpp 复制代码

样例输出 1

cpp 复制代码

YES

样例输入 2

cpp 复制代码

样例输出 2

cpp 复制代码

NO

样例 2 提示

图 A 的邻接矩阵为：

cpp 复制代码

0 1 1
1 0 1
1 1 0

表示图 A 中，节点 1 与节点 2 和节点 3 相连，节点 2 与节点 1 和节点 3 相连，节点 3 与节点 1 和节点 2 相连。

图 B 的邻接表为：

cpp 复制代码

1 2 2 3
2 2 1 3
3 1 1

表示图 B 中，节点 1 与节点 2 和节点 3 相连，节点 2 与节点 1 和节点 3 相连，节点 3 与节点 1 相连。

对比可以发现，在图 B 中，节点 3 不连向节点 2。因此，图 A 和图 B 不完全一样，输出 "NO"。

邻接矩阵

邻接表

题解

cpp 复制代码

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

int main() {
  int n; // 顶点数
  cin >> n;
  vector<vector<int>> adjA(n + 1), adjB(n + 1);

  // 读取并转换图 A
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
      int val;
      cin >> val;
      if (val == 1)
        adjA[i].push_back(j);
    }
  }

  // 读取图 B
  for (int i = 0; i < n; i++) {
    int node, k;
    cin >> node >> k;
    adjB[node].resize(k);
    for (int j = 0; j < k; j++) {
      cin >> adjB[node][j];
    }
  }

  // 对邻接表排序
  for (int i = 1; i <= n; i++) {
    sort(adjA[i].begin(), adjA[i].end());
    sort(adjB[i].begin(), adjB[i].end());
  }

  // 比较邻接表
  bool same = true;
  for (int i = 1; i <= n; i++) {
    if (adjA[i] != adjB[i]) {
      same = false;
      break;
    }
  }

  cout << (same ? "YES" : "NO") << endl;
  return 0;
}