参考资料:B站的视频解析
知乎神经常微分方程总结
论文链接:论文
什么是常微分方程?
微分方程式包含未知函数及其导数的方程,未知函数导数的最高阶数称为给i微分方程的阶。
常微分方程(ordinary differential equation,简称ODE)是未知函数只含有一个自变量的微分方程
F ( x , y , y ′ , y ′ ′ , . . . , y ( n ) ) = 0 F(x,y,y^{^{\prime}},y^{^{\prime\prime}},...,y^{(n)})=0 F(x,y,y′,y′′,...,y(n))=0
f ′ ( x ) − 7 f ( x ) = 0 f^{^{\prime}}(x)-7f(x)=0 f′(x)−7f(x)=0

对输入求解一个为微分方程的解的值。
Neural ODE的核心思想
Neural ODE将神经网络的前向传播视为微分方程的求解过程。具体来说,它用微分方程描述隐藏状态随"时间"的变化:
d h ( t ) d t = f ( h ( t ) , t , θ ) \frac {dh(t)}{dt} = f(h(t), t, θ) dtdh(t)=f(h(t),t,θ)
- h(t)是时间t的隐藏状态
- f是由神经网络参数化的函数(通常是MLP)
- θ是可学习参数
用ODE表示有什么优势
1.Powerful representation:微分方程可以用数值法求解,因此对于任何连续函数都有良好的逼近能力。
2.Memory efficiency:不需要用到反向传播,因此训练上节约内存
3.Simplicity:不需要考虑复杂的调参和网络设计,形式简洁
4.Abstraction:让网络不需要考虑每层需要做什么,只需要考虑怎么计算结果
求解微分方程
因为解析解并不总是好计算的

数值分析的内容。
欧拉法


ResNet与欧拉法的关系


一个是离散的,一个是连续的
.
求解的最大距离,计算步长,迭代更新方程


网络参数更新
不适用反向传播,因为相当于从把离散的值,用连续的值来进行扩散,数值太多了。

所以使用了反向的梯度扩散
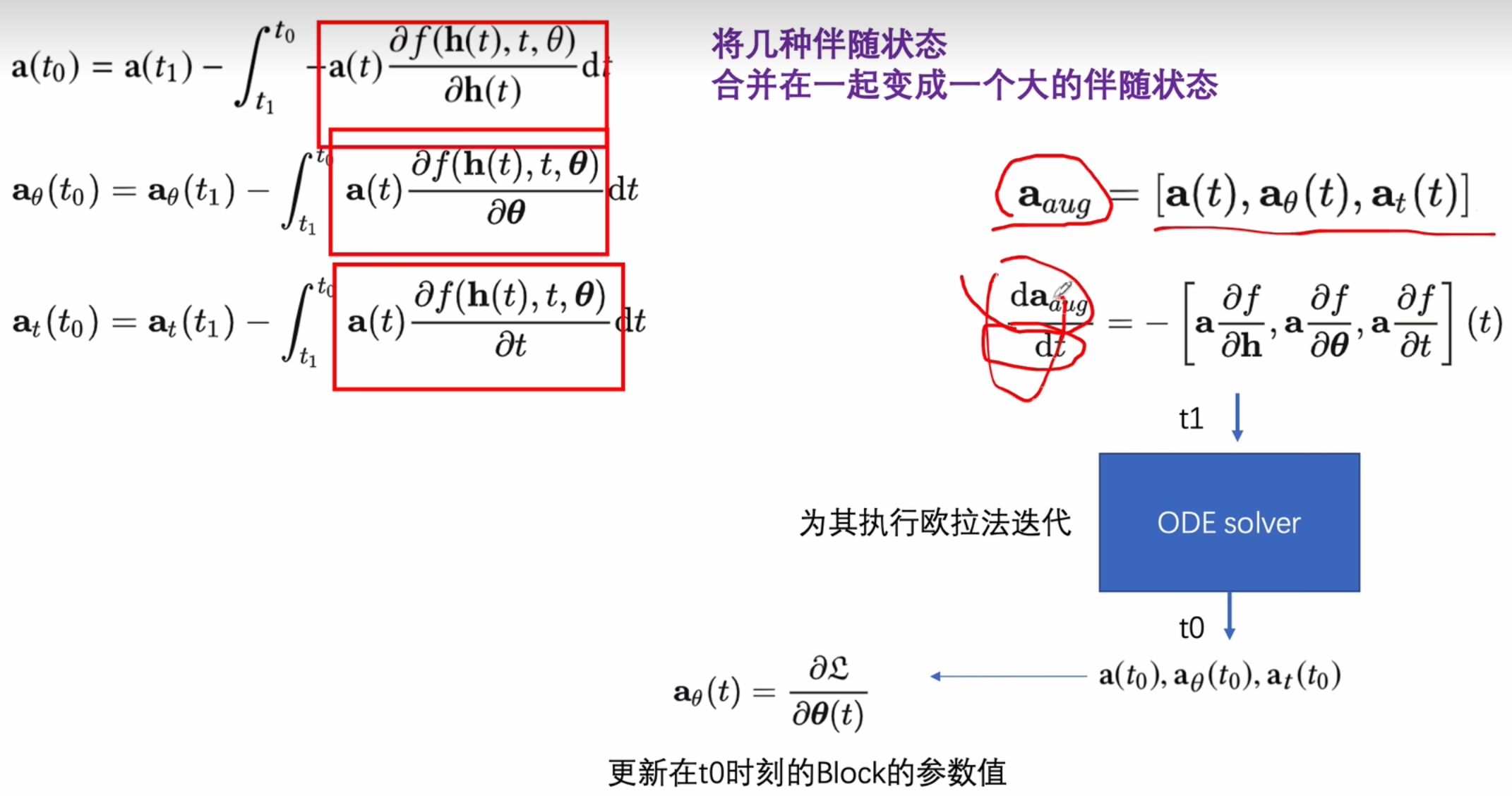
伴随灵敏度法

反向,建立和正向相同数量的state
构建中间的状态


利用了可变积分的定义形式。

和a相关的两个参数的偏微分


性能的对比

code example
ai生成的代码
python
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from torchdiffeq import odeint
matplotlib.rcParams['font.sans-serif']=['SimHei']
matplotlib.rcParams['axes.unicode_minus']=False
# 设置随机种子以确保结果可复现
torch.manual_seed(42)
np.random.seed(42)
# 1. 定义ODE函数
class ODEFunc(nn.Module):
def __init__(self, hidden_dim):
super(ODEFunc, self).__init__()
self.net = nn.Sequential(
nn.Linear(hidden_dim, 2*hidden_dim),
nn.Tanh(),
nn.Linear(2*hidden_dim, hidden_dim)
)
def forward(self, t, x):
return self.net(x)
# 2. 定义ODE块
class ODEBlock(nn.Module):
def __init__(self, odefunc):
super(ODEBlock, self).__init__()
self.odefunc = odefunc
self.integration_times = torch.tensor([0, 1], dtype=torch.float32)
def forward(self, x):
out = odeint(self.odefunc, x, self.integration_times, method='dopri5')
return out[-1] # 返回最终状态
# 3. 定义完整的Neural ODE模型
class NeuralODE(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(NeuralODE, self).__init__()
self.encoder = nn.Linear(input_dim, hidden_dim)
self.ode_block = ODEBlock(ODEFunc(hidden_dim))
self.decoder = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = self.encoder(x)
x = self.ode_block(x)
x = self.decoder(x)
return x
# 4. 创建一个简单的螺旋数据集作为示例
def generate_spiral_data(n_samples=1000, noise=0.2):
theta = np.sqrt(np.random.rand(n_samples)) * 2 * np.pi
# 两个不同的螺旋
r_a = theta + np.pi
data_a = np.stack([
r_a * np.cos(theta) + np.random.randn(n_samples) * noise,
r_a * np.sin(theta) + np.random.randn(n_samples) * noise
], axis=1)
label_a = np.zeros(n_samples)
r_b = -theta - np.pi
data_b = np.stack([
r_b * np.cos(theta) + np.random.randn(n_samples) * noise,
r_b * np.sin(theta) + np.random.randn(n_samples) * noise
], axis=1)
label_b = np.ones(n_samples)
data = np.vstack([data_a, data_b])
label = np.hstack([label_a, label_b])
indices = np.random.permutation(len(data))
return data[indices], label[indices]
# 5. 准备数据
X, y = generate_spiral_data(n_samples=1000, noise=0.2)
X_train = torch.tensor(X, dtype=torch.float32)
y_train = torch.tensor(y, dtype=torch.float32).reshape(-1, 1)
# 6. 初始化模型、损失函数和优化器
input_dim = 2
hidden_dim = 16
output_dim = 1
model = NeuralODE(input_dim, hidden_dim, output_dim)
criterion = nn.BCEWithLogitsLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# 7. 训练模型
n_epochs = 100
losses = []
print("开始训练Neural ODE模型...")
for epoch in range(n_epochs):
optimizer.zero_grad()
# 前向传播
outputs = model(X_train)
loss = criterion(outputs, y_train)
# 反向传播和优化
loss.backward()
optimizer.step()
losses.append(loss.item())
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch+1}/{n_epochs}], Loss: {loss.item():.4f}')
# 8. 可视化训练过程
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(losses)
plt.title('训练损失')
plt.xlabel('Epoch')
plt.ylabel('Loss')
# 9. 可视化决策边界
def plot_decision_boundary(model, X, y):
# 创建网格点
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
# 对网格点进行预测
with torch.no_grad():
grid = torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32)
Z = torch.sigmoid(model(grid)).numpy().reshape(xx.shape)
# 绘制决策边界和数据点
plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.RdBu)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdBu, edgecolors='k')
plt.title('Neural ODE 决策边界')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
# 可视化决策边界
plt.subplot(1, 2, 2)
plot_decision_boundary(model, X, y)
plt.tight_layout()
plt.savefig('neural_ode_results.png')
plt.show()
# 10. 可视化ODE轨迹
def plot_trajectories(model, X, n_samples=5):
# 选择几个样本
indices = np.random.choice(len(X), n_samples, replace=False)
samples = torch.tensor(X[indices], dtype=torch.float32)
# 获取起始隐藏状态
with torch.no_grad():
h0 = model.encoder(samples)
# 创建更多的时间点以可视化轨迹
t = torch.linspace(0, 1, 100)
# 计算轨迹
with torch.no_grad():
trajectories = odeint(model.ode_block.odefunc, h0, t)
# 轨迹形状应该是 [时间点数, 样本数, 隐藏维度]
# 首先转换为正确的形状进行处理
trajectories = trajectories.permute(1, 0, 2) # [样本数, 时间点数, 隐藏维度]
n_samples, n_times, hidden_dim = trajectories.shape
# 降维以便可视化 (使用简化的PCA)
trajectories_flat = trajectories.reshape(-1, hidden_dim) # 展平所有时间点和样本
# 计算协方差矩阵
mean = trajectories_flat.mean(dim=0, keepdim=True)
centered = trajectories_flat - mean
cov = centered.T @ centered / (centered.shape[0] - 1)
# 特征值分解
e, v = torch.linalg.eigh(cov)
# 选择最大的两个特征值/向量
indices = torch.argsort(e, descending=True)
proj_matrix = v[:, indices[:2]] # 投影矩阵使用前两个主成分
# 投影到2D
trajectories_2d = trajectories_flat @ proj_matrix
trajectories_2d = trajectories_2d.reshape(n_samples, n_times, 2) # [样本数, 时间点数, 2]
# 绘制轨迹
plt.figure(figsize=(8, 6))
colors = plt.cm.rainbow(np.linspace(0, 1, n_samples))
for i in range(n_samples):
# 获取当前样本的轨迹
sample_traj = trajectories_2d[i] # [时间点数, 2]
# 绘制完整轨迹
plt.plot(sample_traj[:, 0], sample_traj[:, 1],
'o-', color=colors[i], alpha=0.8, markersize=2,
label=f'Sample {i+1}')
# 标记起点和终点
plt.scatter(sample_traj[0, 0], sample_traj[0, 1],
color=colors[i], s=80, marker='*', label='_')
plt.scatter(sample_traj[-1, 0], sample_traj[-1, 1],
color=colors[i], s=100, marker='x', label='_')
plt.title('Neural ODE 特征空间中的轨迹')
plt.legend()
plt.grid(True)
plt.savefig('neural_ode_trajectories.png')
plt.show()
# 可视化部分样本的ODE轨迹
plot_trajectories(model, X, n_samples=5)
# 11. 评估模型性能
with torch.no_grad():
y_pred = torch.sigmoid(model(X_train))
preds = (y_pred > 0.5).float()
accuracy = (preds == y_train).float().mean()
print(f"模型准确率: {accuracy.item():.4f}")
# 12. 可视化不同时间步的状态演变
def visualize_state_evolution(model, X, sample_idx=0):
# 选择一个样本
sample = torch.tensor(X[sample_idx:sample_idx+1], dtype=torch.float32)
# 获取起始隐藏状态
with torch.no_grad():
h0 = model.encoder(sample)
# 创建更多的时间点以可视化演变
t = torch.linspace(0, 1, 10)
# 计算在不同时间点的状态
with torch.no_grad():
states = odeint(model.ode_block.odefunc, h0, t)
outputs = [model.decoder(state) for state in states]
probs = [torch.sigmoid(output).item() for output in outputs]
# 绘制不同时间步的输出概率
plt.figure(figsize=(8, 5))
plt.plot(t.numpy(), probs, 'o-', linewidth=2)
plt.axhline(y=0.5, color='r', linestyle='--', alpha=0.7)
plt.title(f'样本 {sample_idx} 在ODE求解过程中的输出演变')
plt.xlabel('时间 t')
plt.ylabel('预测概率')
plt.grid(True)
plt.savefig('neural_ode_evolution.png')
plt.show()
# 可视化一个样本的状态演变
visualize_state_evolution(model, X, sample_idx=42)
print("Neural ODE 示例运行完成!")解读
ode函数的定义
ODE函数(通常表示为f(t, x, θ))代表状态随时间的变化率
1. 神经网络参数化
class ODEFunc(nn.Module):
def __init__(self, hidden_dim):
super(ODEFunc, self).__init__()
self.net = nn.Sequential(
nn.Linear(hidden_dim, 2*hidden_dim),
nn.Tanh(),
nn.Linear(2*hidden_dim, hidden_dim)
)
def forward(self, t, x):
return self.net(x)这个神经网络接收当前状态x,输出状态的变化率dx/dt。关键点在于:
输入维度和输出维度必须相同(因为它代表同一状态空间中的变化率)
通常使用简单的MLP结构,但也可以使用更复杂的网络
激活函数的选择会影响ODE流的平滑性,常用Tanh或Softplus等光滑函数
2. 基于物理模型
对于某些领域特定问题,ODE函数可以基于已知的物理规律来定义,例如:
胡克定律:
d 2 x d t 2 = − k m x \frac{d^2x}{dt^2}=-\frac{k}{m}x dt2d2x=−mkx
拆分为两个方程:
{ d x d t = v d v d t = − k m x \begin{cases}\frac{dx}{dt}=v\\\frac{dv}{dt}=-\frac{k}{m}x&\end{cases} {dtdx=vdtdv=−mkx
python
def f(t, x, params):
# 例如简谐振动的微分方程
# 分解状态变量:位置(position)和速度(velocity)
position, velocity = x[..., 0], x[..., 1] # 使用 ... 处理批量维度
# 计算加速度:a = -k/m * x
acceleration = -params['k'] * position / params['m']
# 返回导数 [dx/dt, dv/dt]
return torch.stack([velocity, acceleration], dim=-1)使用示例
python
params = {'k': 2.0, 'm': 1.0} # 弹性系数和质量
x0 = torch.tensor([1.0, 0.0]) # 初始状态 [位置, 速度]
t = 0.0 # 当前时间(方程不显含时间t)
dxdt = f(t, x0, params) # 输出应为 [0.0, -2.0]3. 混合方法
将物理先验与神经网络结合:
python
def f(t, x, params, nn_params):
known_dynamics = physical_model(t, x, params)
unknown_dynamics = neural_network(x, nn_params)
return known_dynamics + unknown_dynamicsODE函数的设计原则
ODE函数的设计不是完全随意的,而是需要满足以下几个要点:
-
维度匹配:输入和输出维度必须相同,确保它真正表示变化率
-
平滑性:ODE求解器需要函数具有一定的平滑性,所以通常使用光滑的激活函数
-
稳定性:函数设计应当避免数值不稳定,例如避免输出极大的值
-
表达能力:函数应当具有足够的能力来表达所需的动态系统
如何选择ODE函数结构
选择ODE函数的结构通常基于以下考虑:
-
问题复杂度:对于简单问题,使用较小的网络;复杂问题则需要更强的表达能力
-
计算效率:复杂的ODE函数会增加求解器的计算负担
-
领域知识:当有领域先验知识时,可以将其编码到ODE函数中
-
实验验证:不同的ODE函数结构可以通过实验比较性能
实践中的调整
在实践中,ODE函数的确定往往遵循以下步骤:
- 从简单的MLP开始
- 调整网络宽度(隐藏层大小)
- 尝试不同的激活函数
- 根据验证集性能进行调整
- 如有领域知识,尝试将其整合到函数中
总结来说,Neural ODE中的函数不是随便定义的,而是根据问题特性、计算考虑和理论要求精心设计的。这个函数需要平衡表达能力、计算效率和数值稳定性。
odeblock
记录了一个odefunc,还有 integration_times积分的时间区间
forward方法中调用odeint进行求解,返回最后一个时间点的结果
表示使用自适应步长的Dormand-Prince 5(4)算法。
时间区间:[0, 1] 是抽象的时间跨度,可以理解为"虚拟时间"上的变换过程,与物理时间无关。
python
# 2. 定义ODE块
class ODEBlock(nn.Module):
def __init__(self, odefunc):
super(ODEBlock, self).__init__()
self.odefunc = odefunc
## 观察多个时间点(t=0, 0.5, 1)
self.integration_times = torch.tensor([0, 1], dtype=torch.float32)
def forward(self, x):
out = odeint(self.odefunc, x, self.integration_times, method='dopri5')
return out[-1] # 返回最终状态NeuralODE
python
# 3. 定义完整的Neural ODE模型
class NeuralODE(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(NeuralODE, self).__init__()
self.encoder = nn.Linear(input_dim, hidden_dim)# 编码器
self.ode_block = ODEBlock(ODEFunc(hidden_dim))# ODE动力学层
self.decoder = nn.Linear(hidden_dim, output_dim) # 解码器
def forward(self, x):
x = self.encoder(x)# 输入 → 隐藏空间
x = self.ode_block(x)# 通过ODE动力学演化
x = self.decoder(x)# 隐藏空间 → 输出
return x组件功能:
| 组件 | 功能 |
|---|---|
| Encoder | 将输入数据 x 从 input_dim 维度映射到 hidden_dim 的隐藏空间。 |
| ODEBlock | 在隐藏空间中通过微分方程定义的连续动力学系统对特征进行非线性变换。 |
| Decoder | 将演化后的隐藏状态映射回目标输出维度 output_dim。 |
3. 关键设计思想
① 连续深度模型
- 与传统神经网络的区别 :
- 传统网络:离散的层(如
nn.Linear+nn.ReLU)堆叠,深度固定。 - Neural ODE:用ODE求解器替代离散层,形成连续深度,允许动态调整"深度"(通过调整积分时间步长)。
- 传统网络:离散的层(如
② 参数效率
- 动力学共享 :所有时间步共享同一个
odefunc定义的动力学方程,参数数量与"深度"无关。 - 隐式正则化:ODE的平滑性天然避免过拟合。
③ 反向传播机制
- 伴随方法 (Adjoint Method) :通过求解伴随ODE 反向传播梯度,无需存储中间状态,内存复杂度为
O(1)(与积分步数无关)。
4. 工作流程示例
假设输入数据维度为 input_dim=3,隐藏层 hidden_dim=5,输出 output_dim=2:
- 编码阶段 :
encoder将输入x(维度3)映射到隐藏空间(维度5)。 - ODE演化 :隐藏状态在ODE定义的向量场中从时间
0演化到1。 - 解码阶段 :最终隐藏状态通过
decoder映射到输出(维度2)。
5. 与物理ODE的类比
如果将隐藏状态视为物理系统的状态:
odefunc:类似物理定律(如牛顿方程),定义状态如何随时间变化。ODEBlock:类似模拟器,根据物理定律演化系统状态。integration_times:模拟的时间跨度,控制演化"深度"。
6. 潜在扩展方向
- 复杂动力学 :在
ODEFunc中设计更复杂的微分方程(如引入非线性、外部控制项)。 - 可变时间跨度 :动态调整
integration_times实现自适应深度。 - 混合架构:将ODEBlock与传统神经网络层结合。
通过这种设计,Neural ODE 提供了一种连续、可逆且参数高效的建模方式,特别适合处理时序数据或需要连续变换的任务。
data
使用一个生成的数据集
python
# 4. 创建一个简单的螺旋数据集作为示例
def generate_spiral_data(n_samples=1000, noise=0.2):
theta = np.sqrt(np.random.rand(n_samples)) * 2 * np.pi
# 两个不同的螺旋
r_a = theta + np.pi
data_a = np.stack([
r_a * np.cos(theta) + np.random.randn(n_samples) * noise,
r_a * np.sin(theta) + np.random.randn(n_samples) * noise
], axis=1)
label_a = np.zeros(n_samples)
r_b = -theta - np.pi
data_b = np.stack([
r_b * np.cos(theta) + np.random.randn(n_samples) * noise,
r_b * np.sin(theta) + np.random.randn(n_samples) * noise
], axis=1)
label_b = np.ones(n_samples)
data = np.vstack([data_a, data_b])
label = np.hstack([label_a, label_b])
indices = np.random.permutation(len(data))
return data[indices], label[indices]
# 5. 准备数据
X, y = generate_spiral_data(n_samples=1000, noise=0.2)
X_train = torch.tensor(X, dtype=torch.float32)
y_train = torch.tensor(y, dtype=torch.float32).reshape(-1, 1)模型的初始化
python
# 6. 初始化模型、损失函数和优化器
input_dim = 2 # 模型输入维度(如二维特征)
hidden_dim = 16 # ODE隐藏状态维度
output_dim = 1 # 模型输出维度(如二分类概率)
model = NeuralODE(input_dim, hidden_dim, output_dim)
criterion = nn.BCEWithLogitsLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)类似于传统深度学习中的"编码-处理-解码"范式,但用ODEBlock替代了离散的中间层。
python
# 测试数据
x = torch.randn(32, input_dim) # batch_size=32, input_dim=2
# 前向传播
h = model.encoder(x) # 输出形状: (32, 16)
h_ode = model.ode_block(h) # 输出形状: (32, 16)
output = model.decoder(h_ode) # 输出形状: (32, 1)训练过程
python
# 7. 训练模型
n_epochs = 50
losses = []
print("开始训练Neural ODE模型...")
for epoch in range(n_epochs):
optimizer.zero_grad()
# 前向传播
outputs = model(X_train)
loss = criterion(outputs, y_train)
# 反向传播和优化
loss.backward()
optimizer.step()
losses.append(loss.item())
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch+1}/{n_epochs}], Loss: {loss.item():.4f}')
# 8. 可视化训练过程
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(losses)
plt.title('训练损失')
plt.xlabel('Epoch')
plt.ylabel('Loss')决策边界
预测出来的是坐标(x,y)在这个里面的分类
python
# 9. 可视化决策边界
def plot_decision_boundary(model, X, y):
# 创建网格点
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
# 对网格点进行预测
with torch.no_grad():
grid = torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32)
Z = torch.sigmoid(model(grid)).numpy().reshape(xx.shape)
# 绘制决策边界和数据点
plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.RdBu)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdBu, edgecolors='k')
plt.title('Neural ODE 决策边界')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
# 可视化决策边界
plt.subplot(1, 2, 2)
plot_decision_boundary(model, X, y)
plt.tight_layout()
plt.savefig('neural_ode_results.png')
plt.show()
可视化ODE轨迹
这个的意义不是很清晰。随着批次进行,某个样本点的hidden层的特征的主要部分的值变化。
python
# 10. 可视化ODE轨迹
def plot_trajectories(model, X, n_samples=5):
# 选择几个样本
indices = np.random.choice(len(X), n_samples, replace=False)
samples = torch.tensor(X[indices], dtype=torch.float32)
# 获取起始隐藏状态
with torch.no_grad():
h0 = model.encoder(samples)
# 创建更多的时间点以可视化轨迹
t = torch.linspace(0, 1, 100)
# 计算轨迹
with torch.no_grad():
trajectories = odeint(model.ode_block.odefunc, h0, t)
# 轨迹形状应该是 [时间点数, 样本数, 隐藏维度]
# 首先转换为正确的形状进行处理
trajectories = trajectories.permute(1, 0, 2) # [样本数, 时间点数, 隐藏维度]
n_samples, n_times, hidden_dim = trajectories.shape
# 降维以便可视化 (使用简化的PCA)
trajectories_flat = trajectories.reshape(-1, hidden_dim) # 展平所有时间点和样本
# 计算协方差矩阵
mean = trajectories_flat.mean(dim=0, keepdim=True)
centered = trajectories_flat - mean
cov = centered.T @ centered / (centered.shape[0] - 1)
# 特征值分解
e, v = torch.linalg.eigh(cov)
# 选择最大的两个特征值/向量
indices = torch.argsort(e, descending=True)
proj_matrix = v[:, indices[:2]] # 投影矩阵使用前两个主成分
# 投影到2D
trajectories_2d = trajectories_flat @ proj_matrix
trajectories_2d = trajectories_2d.reshape(n_samples, n_times, 2) # [样本数, 时间点数, 2]
# 绘制轨迹
plt.figure(figsize=(8, 6))
colors = plt.cm.rainbow(np.linspace(0, 1, n_samples))
for i in range(n_samples):
# 获取当前样本的轨迹
sample_traj = trajectories_2d[i] # [时间点数, 2]
# 绘制完整轨迹
plt.plot(sample_traj[:, 0], sample_traj[:, 1],
'o-', color=colors[i], alpha=0.8, markersize=2,
label=f'Sample {i+1}')
# 标记起点和终点
plt.scatter(sample_traj[0, 0], sample_traj[0, 1],
color=colors[i], s=80, marker='*', label='_')
plt.scatter(sample_traj[-1, 0], sample_traj[-1, 1],
color=colors[i], s=100, marker='x', label='_')
plt.title('Neural ODE 特征空间中的轨迹')
plt.legend()
plt.grid(True)
plt.savefig('neural_ode_trajectories.png')
plt.show()
# 可视化部分样本的ODE轨迹
plot_trajectories(model, X, n_samples=5)
先学习到这里。有应用的话,在进行补充。