在大规模深度学习时代,训练拥有数十亿甚至上万亿参数的巨型模型(如 GPT-3、LLaMA)对优化器提出了严苛的挑战。传统的随机梯度下降(SGD)或 Adagrad 等方法,往往因收敛速度慢、对学习率(Learning Rate)敏感等问题而难以胜任。Adam(Adaptive Moment Estimation)优化器凭借其融合**动量(Momentum)和自适应学习率(Adaptive Learning Rate)**的双重优势,在非凸优化空间中展现出卓越的稳定性和效率,已成为大模型训练的首选方案。
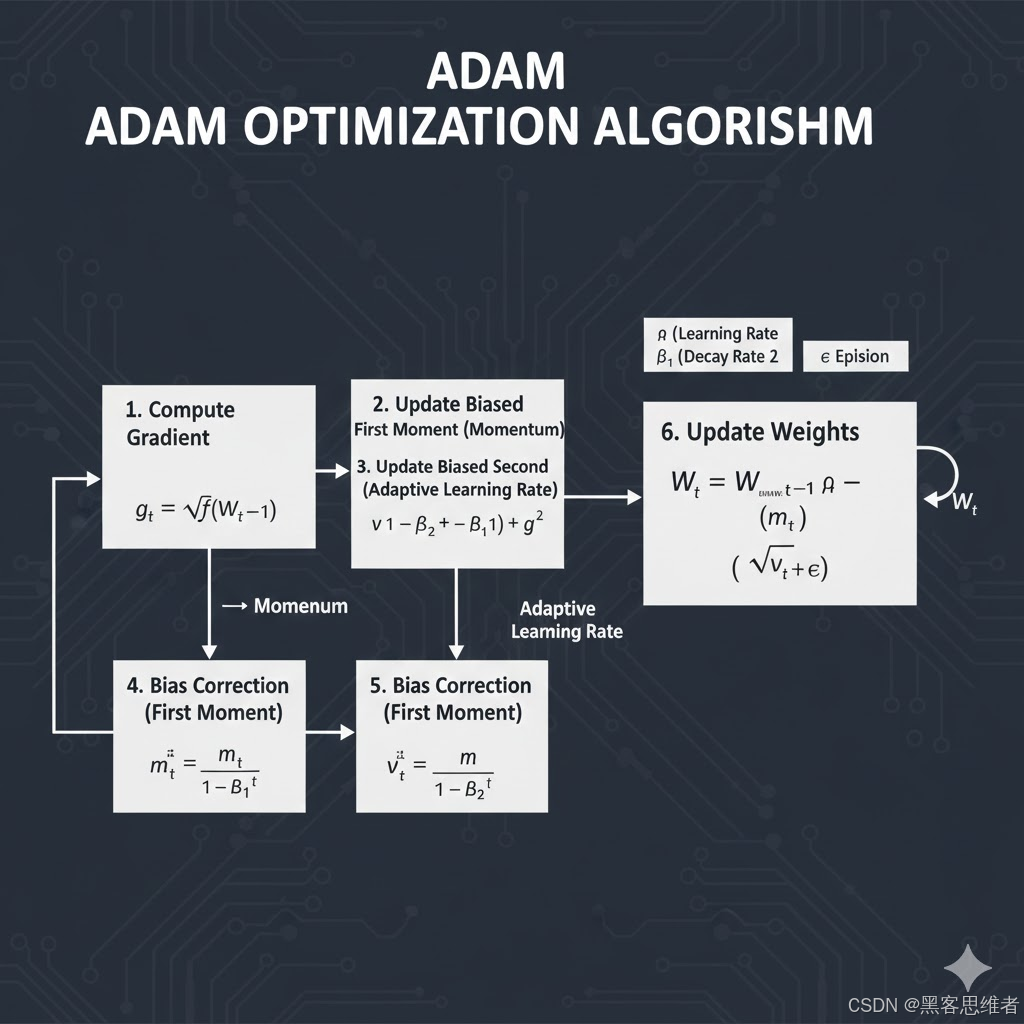
1. 大规模训练中的传统优化器困境
在模型参数量较小或数据集较小时,SGD 配合动量(SGD with Momentum)通常能取得稳健的结果。但面对大模型的训练场景,有两个核心问题使得传统方法效率低下:
1.1 梯度稀疏与学习速度不均
在自然语言处理(NLP)和大规模推荐系统等领域,数据通常是高维且稀疏的。许多特征的梯度更新频率极低,导致它们的权重更新非常缓慢。
- SGD 的问题: SGD 对所有参数都使用相同的全局学习率。对于那些更新频率低的参数,其学习率过小;而对于更新频率高的参数,学习率又可能过大,导致震荡。
1.2 优化空间复杂性与鞍点挑战
大型神经网络的损失函数曲面是极其复杂的非凸空间,充满了大量的**鞍点(Saddle Points)**而非真正的局部极小值。SGD 在鞍点附近由于梯度接近于零,很容易被困住,导致收敛停滞。
2. Adam 的核心机制:动量与自适应的完美融合
Adam 优化器的成功在于巧妙地结合了两个关键思想:一阶动量和二阶动量,从而解决了上述痛点。
2.1 融合动量:平滑方向(一阶矩)
Adam 借鉴了 SGD with Momentum 的思想,引入了一阶矩估计(First Moment Estimate) ,即指数加权移动平均的梯度 mtm_tmt。
mt=β1mt−1+(1−β1)gtm_t = \beta_1 m_{t-1} + (1 - \beta_1) g_tmt=β1mt−1+(1−β1)gt
这里的 mtm_tmt 可以理解为梯度在历史上的平均值,它赋予了优化方向"惯性"或动量。这能有效平滑 SGD 带来的随机性震荡,尤其是在损失曲面比较崎岖的峡谷地带,帮助参数快速冲过鞍点。
2.2 自适应学习率:定制化速度(二阶矩)
Adam 的革命性在于引入了二阶矩估计(Second Moment Estimate) ,即指数加权移动平均的梯度平方 vtv_tvt。
vt=β2vt−1+(1−β2)gt2v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2vt=β2vt−1+(1−β2)gt2
vtv_tvt 衡量的是每个参数的历史梯度幅度的平均平方。它本质上捕捉了每个参数的稀疏性 和波动性 。Adam 利用 vt\sqrt{v_t}vt 来动态调整学习率:
ηt=ηvt+ϵ⋅mt\eta_t = \frac{\eta}{\sqrt{v_t} + \epsilon} \cdot m_tηt=vt +ϵη⋅mt
- 对稀疏参数: 如果一个参数的梯度 gtg_tgt 很少出现(稀疏),那么 vtv_tvt 就会很小,最终导致 1vt\frac{1}{\sqrt{v_t}}vt 1 很大,从而提高该参数的学习率。
- 对频繁参数: 如果一个参数的梯度 gtg_tgt 频繁出现,那么 vtv_tvt 保持较大,学习率会被降低。
这种机制使得 Adam 对超参数学习率 η\etaη 的初始设置不敏感,因为它会自动为每个参数定制最合适的学习速度。这极大地减轻了大规模训练中学习率调参的负担。
3. 案例分析:大模型训练中的稳定表现
案例:Transformer 架构的训练
大型语言模型(LLMs)普遍采用 Transformer 架构,其特点是:
- 梯度不均: Embedding 层和最后的 Logit 层参数量大、梯度更新频率高;而中间的 Multi-Head Attention 层梯度相对平缓。
- 深度与复杂性: 网络层数深,优化空间极其复杂。
Adam 的作用: Adam 为 Embedding 层等更新频繁的参数降低学习率,防止其过度震荡,同时为 Attention 层的参数提供稳定的动量,使其能够有效地在复杂的优化曲面中推进。这种参数级别的收敛速度控制是 Adam 能够在大规模 Transformer 训练中保持稳定和快速收敛的关键。
4. AdamW:解决泛化性问题的关键变种
Adam 虽快,但其原始的权重衰减(Weight Decay)方式存在一个缺陷,这曾是其泛化性不如 SGD 的主要原因。
4.1 原始 Adam 的陷阱
在原始 Adam 中,权重衰减(L2L_2L2 正则化)与自适应学习率机制是耦合 的。权重衰减项被包含在二阶矩 vtv_tvt 的计算中。
- 问题: 学习率较大的参数,其权重衰减效果反而被削弱;而学习率较小的参数(通常是贡献小的参数),其权重衰减效果却被过度放大。这违背了权重衰减原本的意图。
4.2 AdamW 的分离(Decoupling)策略
AdamW 提出的核心改进是将权重衰减项从梯度更新中分离出来,单独应用于权重更新。
权重更新=Adam 更新−λ⋅Wt\text{权重更新} = \text{Adam 更新} - \lambda \cdot W_t权重更新=Adam 更新−λ⋅Wt
其中 λ\lambdaλ 是权重衰减系数,WtW_tWt 是当前权重。
- 效果: AdamW 确保了权重衰减的强度不再受参数历史梯度波动(即 vtv_tvt)的影响,从而实现了更有效的正则化。这使得 AdamW 在保持 Adam 快速收敛的同时,显著提高了模型的泛化性,减少了在大模型上常见的过拟合风险。
总结
Adam 优化器凭借其独特的动量与自适应学习率机制,为大规模神经网络训练提供了高效率、高稳定性和对超参数的低敏感性 。而 AdamW 变种的引入,通过解耦权重衰减,彻底解决了原始 Adam 在泛化性上的不足。因此,无论是追求速度还是追求最终精度,AdamW 都成为了当前训练数十亿级参数模型的默认启动器。