定义一个3D cube,并计算cube每个顶点的像素坐标
scratch a pixel课程:Your Starting Point!


3D场景中物体所有点与坐标系原点的连线,该连线与像素平面canvas的交点就是场景中3D点其投影点的位置

3D场景中的点均由这个坐标系描述

相似三角形ABC和A'B'C',由相似性得到:
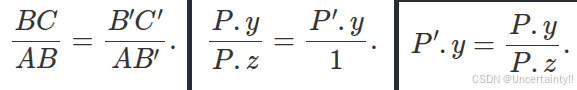
像素平面为z=-1处的平面
3D顶点在像素平面上的y'坐标=3D点的y坐标/该点深度z(也就是透视除法perspective divide)
同理,3D顶点在像素平面上的x'坐标=3D点的x坐标/该点深度z
3D顶点P的z值为负值,若P的x值为正,则投影后变为了负值,因为除以了z值(负数),若P的x值为负,则投影后变为了正值

这种投影是正交投影,也就是没有近大远小的效果
cpp
#include<iostream>
typedef float Point[3]; //定义了一个类型别名point,它表示一个包含3个float类型元素的数组,一个点三个float
int main() {
//represent the box,每个元素为Point类型
Point corners[8] = {
{ 1, -1, -5},
{ 1, -1, -3},
{ 1, 1, -5},
{ 1, 1, -3},
{-1, -1, -5},
{-1, -1, -3},
{-1, 1, -5},
{-1, 1, -3}
};
//projection
for (int i=0; i < 8; i++) {
float x_proj = corners[i][0] / -corners[i][2];
float y_proj = corners[i][1] / -corners[i][2];
printf("Projected corner %d: x:%f, y:%f\n", i, x_proj, y_proj);
}
return 0;
}
我们发现投影点坐标有正有负,因为像素坐标都是正的,所以我们需要对以上坐标进行重新映射
cpp
#include<iostream>
typedef float Point[3]; //定义了一个类型别名point,它表示一个包含3个float类型元素的数组,一个点三个float
int main() {
//represent the box,每个元素为Point类型
Point corners[8] = {
{ 1, -1, -5},
{ 1, -1, -3},
{ 1, 1, -5},
{ 1, 1, -3},
{-1, -1, -5},
{-1, -1, -3},
{-1, 1, -5},
{-1, 1, -3}
};
//projection
for (int i=0; i < 8; i++) {
//坐标范围[-1,1]
float x_proj = corners[i][0] / -corners[i][2];
float y_proj = corners[i][1] / -corners[i][2];
//printf("Projected corner %d: x:%f, y:%f\n", i, x_proj, y_proj);
//坐标范围重映射[-1,1] -> + 1 -> [0,2] -> /2 -> [0,1]
float x_proj_remap = (1 + x_proj)/2;
float y_proj_remap = (1 + y_proj)/2;
printf("After remapping,Projected corner %d: x:%f, y:%f\n", i, x_proj_remap, y_proj_remap);
}
return 0;
}坐标范围从[-1,1](屏幕空间,screen space)重映射到了[0,1](NDC空间,Normalized Device Coordinates)
重映射到NDC空间有什么好处?
为了后续可以适应不同大小的图片,我们首先将投影点映射到一个标准的空间,随后根据不同的图片大小进行再次适应性的变换。个人理解:想要呈现的图片大小可能是不一样的,我写一个渲染程序要同时适应这些不同大小的图片,就需要首先将它们统一到一个标准的空间,随后根据不同的图片大小来适应性的做出改变。

假设图片大小为512*512,我们对NDC空间中的点坐标进行变换
cpp
#include<iostream>
typedef float Point[3]; //定义了一个类型别名point,它表示一个包含3个float类型元素的数组,一个点三个float
int main() {
//represent the box,每个元素为Point类型
Point corners[8] = {
{ 1, -1, -5},
{ 1, -1, -3},
{ 1, 1, -5},
{ 1, 1, -3},
{-1, -1, -5},
{-1, -1, -3},
{-1, 1, -5},
{-1, 1, -3}
};
//define image width and height
const unsigned int image_width = 512, image_height = 512;
//projection
for (int i=0; i < 8; i++) {
//坐标范围[-1,1]
float x_proj = corners[i][0] / -corners[i][2];
float y_proj = corners[i][1] / -corners[i][2];
//printf("Projected corner %d: x:%f, y:%f\n", i, x_proj, y_proj);
//坐标范围重映射[-1,1] -> + 1 -> [0,2] -> /2 -> [0,1]
float x_proj_remap = (1 + x_proj)/2;
float y_proj_remap = (1 + y_proj)/2;
//printf("After remapping,Projected corner %d: x:%f, y:%f\n", i, x_proj_remap, y_proj_remap);
float x_proj_pix = x_proj_remap * image_width;
float y_proj_pix = y_proj_remap * image_height;
printf("After transforming to image size,Projected corner %d: x:%f, y:%f\n", i, x_proj_pix, y_proj_pix);
}
return 0;
}
上述计算结果还有小数点,而真实的像素坐标是整数,所以需要对结果进行round off
cpp
#include<cmath>
float x_proj_pix = round(x_proj_remap * image_width);
float y_proj_pix = round(y_proj_remap * image_height);
如果图片大小不是1:1,而是16:9,那么坐标应该如何变换?
一般来说,我们会用到投影矩阵(projection matrix)进行投影,投影矩阵会考虑图像的长宽比(aspect),也就是图像宽度和高度之间的比例。如果这个比率不是1(图像不是正方形的),那么投影矩阵就会正确地考虑到这图片不是方形的,也就是说投影矩阵已经考虑了图片的长宽比
aspect ratio = width height \text{aspect ratio}=\frac{\text{width}}{\text{height}} aspect ratio=heightwidth
可以通过两种方式实现图片为非正方形时的坐标变换
1.您可以计算图像的宽高比,如前所述:宽度除以高度(假设这里的宽度大于高度),然后将投影点的x坐标除以该宽高比(x/aspect),或者将y投影坐标乘以宽高比(y*aspect),这两种操作会给你不同的图像。
x / a s p e c t (可以用这种) y ∗ a s p e c t (或者用这种) x/aspect(可以用这种) ~\\ y*aspect(或者用这种) x/aspect(可以用这种) y∗aspect(或者用这种)
在这两种操作方式下,立方体都会正确地投影到图像表面上,而在第二种情况下,立方体会显得更大,如下图所示。
在该图像中,白色区域代表原始的正方形图像,灰色区域代表非正方形图像。正如您在左边的第一张图像中看到的,正方形图像的顶部和底部边缘与非正方形图像的顶部和底部边缘相匹配。在第二种情况下,在右边,正方形图像的左右边缘分别与非正方形图像的左右边缘相匹配,导致里面的立方体看起来更大。
cpp
#include<iostream>
#include<cmath>
typedef float Point[3]; //定义了一个类型别名point,它表示一个包含3个float类型元素的数组,一个点三个float
int main() {
//represent the box,每个元素为Point类型
Point corners[8] = {
{ 1, -1, -5},
{ 1, -1, -3},
{ 1, 1, -5},
{ 1, 1, -3},
{-1, -1, -5},
{-1, -1, -3},
{-1, 1, -5},
{-1, 1, -3}
};
//define image width and height
const unsigned int image_width = 640, image_height = 480;
float aspect_ratio = image_width / image_height;
//projection
for (int i=0; i < 8; i++) {
//坐标范围[-1,1]
float x_proj = corners[i][0] / -corners[i][2] / aspect_ratio; //option1:divide by aspect
float y_proj = corners[i][1] / -corners[i][2];//(或者这里*aspect)
//printf("Projected corner %d: x:%f, y:%f\n", i, x_proj, y_proj);
//坐标范围重映射[-1,1] -> + 1 -> [0,2] -> /2 -> [0,1]
float x_proj_remap = (1 + x_proj)/2;
float y_proj_remap = (1 + y_proj)/2;
//printf("After remapping,Projected corner %d: x:%f, y:%f\n", i, x_proj_remap, y_proj_remap);
float x_proj_pix = round(x_proj_remap * image_width);
float y_proj_pix = round(y_proj_remap * image_height);
printf("After transforming to image size,Projected corner %d: x:%f, y:%f\n", i, x_proj_pix, y_proj_pix);
}
return 0;
}使用 x/aspect 的结果


使用 y*aspect 的结果

