平衡二叉搜索树模拟实现1-------AVL树(插入,删除,查找)

本章目标

1.AVL树的概念

2.AVL树的模拟实现

1.AVL树的概念

1.AVL树是最先被发明的平衡二叉搜索树,AVL树是一颗空树或者具有以下的性质

它的左右子树都是AVL树,并且左右高度差不超过1,AVL树是一颗高度平衡二叉搜索树,通过高度差去控制平衡

2.为什么高度差是1?

当结点个数为8的情况举例

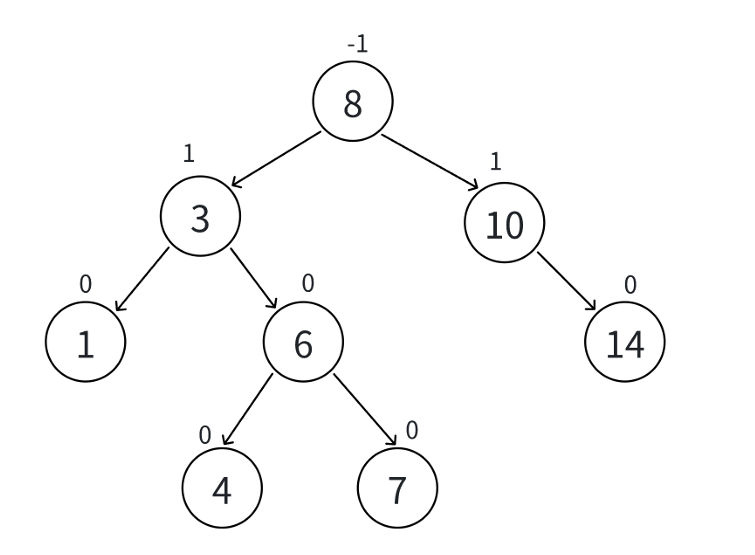
因为如果为0的话,条件过于苛刻了,这种情况是永远无法达到左右高度差为0的.

最好的情况下n-1层以上是完全二叉树,但是仍然会多出来一个结点让高度差为1.

3.AVL树得名于它的发明者G.M.Adelson-Velsky和E.M.Landis是两个前苏联的科学家，他们在1962年的论文《Analgorithmfortheorganizationofinformation》中发表了它。

4.AVL树的实现我们在这里引入了一个平衡因子的概念,每一个结点都有平衡因子,在这里我们规定平衡因子的计算为,右子树高度-左子树高度,也就是在这里平衡因子只有三种可能值,-1/0/1.AVL树并不是一定要平衡因子,我们只是在这里选择使用平衡因子这种方式去实现AVL树,我们通过平衡因子去控制每一个结点的高度让这课树变得平衡.

(如上的中每个结点上面的数字,就是平衡因子)

5.AVL树的整体结构是和完全二叉树类似的,所以搜索效率是logn,相对于二叉搜索树是本质的提升

6.在这里引入平衡因子我们一眼就可以看出以下这颗树不是AVL树因为下面这个2的结点左右高度差为2了.

2.AVL树的模拟实现

因为对于map和set,它们的底层是红黑树,这也是一种平衡二叉搜索树,它们底层的key和Value是用pair封装的,我们这里也使用pair封装,AVL树的实现不只有一种,在这里我们使用三叉链的方式实现,多增加一个parents指针去记忆父节点.在这里还有另一种实现思路是用栈实现.在这里推荐参考殷人昆老师的<<数据结构(用面向对象方法与c++语言描述)>>里面有详细记载用stack去记忆父节点去实现AVL树的方式,我们在这里不过多展开.相对于正常二叉搜索树在这里我们还增加了一个变量去记录平衡因子.

为了泛型编程,我们使用模板去控制数据类型

以下就是AVL树结点的结构

template<class K,class V>
struct AVLTree_Node
{
	typedef AVLTree_Node<K,V> Node;
	pair<K, V> _kv;
	Node* left;
	Node* right;
	Node* parents;
	
	int pf;
	AVLTree_Node(const pair<K,V>& data)
		:left(nullptr)
		,right(nullptr)
		,parents(nullptr)
		,_kv(data)
		,pf(0)
	{
	}
};

2.1插入

对于AVL树的插入过程来说,它只是在二叉搜索树过程中增加了两个部分,更新平衡因子,根据平衡因子进行调整.

因为我们新增一个结点是可能会印象整棵树的高度的,我们要不断更新二叉树中的平衡因子直到达到结束条件,结束条件我们后续会详细分析

对于不平衡的结点我们通过旋转进行调节.旋转的本质是降低高度,且不会影响上一层

2.1.2平衡因子更新规则

在前面我们规定了

1.平衡因子的大小 = 右子树的高度-左子树的高度

2.在这里只有树的高度出现变化才会影响平衡因子

3.我们在左子树进行插入相当于parents的平衡因子--,我们在右子树进行插入的话相当于parents的平衡因子++.

4.parents的平衡因子会决定是否往上更新

2,1.3停止条件

1.如果在更新完平衡因子之后,parents的平衡因子为0的话,我们就停止更新,因为parents在更新前只有两种可能,parents为-1或者1.也就是对于它的左右子树来说是一边高一边低的情况.我们插入结点到parents低的那一边,但对于parents所在的那条子树来说,它的整体高度并没有发生改变.不会影响parents的父节点的平衡因子,更新结束.

2.如果在更新完平衡因子之后,parents的平衡因子为1或者-1的话,我们就继续更新,因为在没有更新之前parents的平衡因子为0,也就是说它是平衡的,在我们新增一个结点之后parents的高度发生改变,它的改变必然引起parents的parents的结点发生改变.要继续更新

3.如果更新之后parents的结点的高度为2/-2,这也就说明parents之前为一高一低的情况,并且我们插入结点的时候也插入到高的那一边,这样就导致了该AVL不平衡了要进行旋转处理.

旋转的目的有两个

(1)让parents这棵子树平衡

(2)降低高度,恢复插入前的高度差,旋转之后无需更新,

4.更新到根如果根为-1/1,也结束.

插入的大概逻辑

bool insert(const pair<K,V>& val)
{
	//插入
	if (root == nullptr)
	{
		root = new Node(val);
		return true;
	}
	Node* cur = root;
	Node* parents = nullptr;
	while (cur)
	{
		if (cur->_kv.first<val.first)
		{
			parents = cur;
			cur = cur->right;
		}
		else if (cur->_kv.first > val.first)
		{
			parents = cur;
			cur = cur->left;
		}
		else
		{
			return false;
		}
	}
	//链接结点
	cur = new Node(val);
	if (val.first<parents->_kv.first)
	{
		cur->parents = parents;
		parents->left = cur;
	}
	else
	{
		cur->parents = parents;
		parents->right = cur;
	}
	//平衡因子
	while (parents)
	{
		//调整平衡因子
		if (cur == parents->left)
		{
			parents->pf--;
		}
		else if(cur==parents->right)
		{
			parents->pf++;
		}
		if (parents->pf == -1 || parents->pf == 1)
		{
			//更新
			cur = parents;
			parents = parents->parents;
		}
		else if(parents->pf==0)
		{
			//结束
			break;
		}
		else if (parents->pf == 2 || parents->pf == -2)
		{
			//旋转处理
			break;
		}
		else
		{
			assert(false);
		}
	}
	return true;
}

在这里,我们因为增加一个parents指针去进行维护父节点,所以在间接时也应该考虑.

2.2旋转

旋转出现时为了解决树出现不平衡的情况,它应该遵守以下规则

1.保持搜索树的规则

2.让不平衡的树变得平衡,降低树的高度.

旋转分为四种:右单旋/左单旋/左右双旋/右左双旋

2.2.1右单旋

在这里我们有一颗根为10的树,并有抽象为a/b/c三种类型的子树,三者均满足AVL树的要求,10可能时整棵树的根,也可能是局部的根,因为旋转的情况有很多种我们在这里并不会进行枚举,抽象为a/b/c来进行表示,下面也会用抽象的例子举例,不过多解释

右单旋主要的解决的是左边高的那边左边高,我们在a插入一个结点,让10不平衡,因为10的左边过高,所以要让10向右边旋转.

右单旋的核心规则

1.因为b的值是介于5和10之间的,我们把b给10的左边,让10成为5的右边,5成为整棵树的根.这样控制了平衡同时使高度重新回到了h+2.如果10为局部根就不需要继续调整了

2.右单旋出现条件cur的平衡因子为-1&&parents的平衡因子为-2

右单旋实现代码

void RotateR(Node* parents)
{
	//保存结点
	Node* subL = parents->left;
	Node* subLR = subL->right;
	//调整顺序
	
	parents->left = subLR;
	if (subLR != nullptr)
	{
		subLR->parents = parents;
	}
	Node* prevparents = parents->parents;
	subL->right = parents;
	parents->parents = subL;
	if (parents == root)
	{
		root = subL;
		subL->parents = nullptr;
	}
	else
	{
		if (prevparents->left == parents)
		{
			prevparents->left = subL;
		}
		else if (prevparents->right == parents)
		{
			prevparents->right = subL;
		}
		else
		{
			assert(false);
		}
		subL->parents = prevparents;
	}
	subL->pf = parents->pf = 0;
}

1.在这里我们要提出几点subLR的结点时三个我们要进行操作的结点中唯一一个可能为空的,我们要进行判断.后面我们去更新parents的时候就可能发生空指针的解引用,

2.如果根为局部根的话,要提前进行保存parents的parents,我们要更新parents的父节点的同时,要判断新的根在原来父结点的左边还是右边

3.更新后的平衡因子parents和subL均平衡所以为0.

4.如果更新的parents为根结点,我们要特殊处理,因为根结点没有父亲,同时修改root

2.2.2左单旋

左单旋处理的情况是右边高的右边高.因为右边太高,我们要让10向左边旋转,控制平衡,同时使高度回到h+2.

左单选的旋转规则

1.因为b的值是介于10和15之间的,我们让b成为10的左=右边,10成为15的左边,15成为新的根

2.左单选出现的情况是cur的平衡因子为1&&parents的平衡因子2.

void RotateL(Node* parents)
{
	Node* subR = parents->right;
	Node* subRL = subR->left;
	
	parents->right = subRL;
	if (subRL != nullptr)
	{
		subRL->parents = parents;
	}
	Node* prevparents = parents->parents;
	subR->left = parents;
	parents->parents = subR;
	if (prevparents == nullptr)
	{
		root = subR;
		subR->parents = nullptr;
	}
	else
	{
		if (prevparents->left == parents)
		{
			prevparents->left = subR;

		}
		else if (prevparents->right == parents)
		{
			prevparents->right = subR;
			//dadada
		}
		else
		{
			assert(false);
		}
		subR->parents = prevparents;
	}
	parents->pf =0, subR->pf = 0;

}

在这里的注意事项与右单旋一致.

2.2.3左右双旋

通过以上两张图,我们可以看到,如果我们插入数据如果在b的位置的话,仅仅单旋是解决不了问题的,它会让左边的高的右边高变为右边高的左边高.我们就要通过两次旋转解决.

因为涉及两次旋转,我们要将b展开进行讨论,分为以下三种情况

(1)场景1当h>=1的时候,我们插入在e子树使8的平衡因为为-1,5为-1,10为-2,不平衡旋转之后,parents的平衡因子为1,剩下两个均为0.

(2)场景2当h>=1的时候,我们插入到f子树,使8的平衡因子变为1,5为-1,10为-2,不平衡旋转之后,subL的平衡因子为-1,剩下两个均为0.

(3)场景3,当h==0的时候,这个时候为新插入的结点,为新增结点,不断更新之后,旋转不平衡,三者旋转后的平衡因子均为0.

在这里我们以第二种情况进行旋转的举例,本质上就是把8的左右结点分别给了两个其他结点.,其他的旋转是类似的

void RotateLR(Node* parents)
{
	Node* subL = parents->left;
	Node* subLR = subL->right;
	int pf = subLR->pf;
	RotateL(parents->left);
	RotateR(parents);
	if (pf == 0)
	{
		subL->pf = 0;
		subLR->pf = 0;
		parents->pf = 0;
	}
	else if (pf == -1)
	{
		parents->pf = 1;
		subL->pf = 0;
		subLR->pf = 0;
	}
	else if (pf == 1)
	{
		parents->pf = 0;
		subL->pf = -1;
		subLR->pf = 0;
	}
	else
	{
		assert(false);
	}
}

在这里要注意提前保存subL,和subLR以及subLR的平衡因子,因为进行单旋的时候会更新平衡因子,我们要根据subLR的平衡因子进行调整新的平衡因子.

2.2.4右左双旋

跟左右双旋类似，下面我们将a/b/c子树抽象为高度h的AVL子树进行分析，另外我们需要把b子树的细节进⼀步展开为12和左子树高度为h-1的e和f子树，因为我们要对b的父亲15为旋转点进行右单旋，右单旋需要动b树中的右⼦树。b子树中新增结点的位置不同，平衡因子更新的细节也不同，通过观察12的平衡因子不同，这里我们要分三个场景讨论。

(1)场景1,当h>=1的时候,我们插入在e子树的时候,会导致12的平衡因子变为-1,15的平衡因子变为-1,10的平衡因子变为2,导致不平衡需要旋转处理,处理之后,subR的平衡因子变为1,其他为0

(2)场景2,当h>=1的时候,我们插入到f子树的时候,会导致12的平衡因子变为1,15的平衡因子变为-1,10的平衡因子变为2不平衡旋转处理后,parents的平衡因子1变为-1,其他为0

(3)场景3,当h==0的时候,我们插入相当于新增结点,会直接导致不平衡发生旋转,旋转后三者的平衡因子均为0.

void RotateRL(Node* parents)
{
	Node* subR = parents->right;
	Node* subRL = subR->left;
	int pf = subRL->pf;
	RotateR(parents->right);
	RotateL(parents);
	if (pf == 0)
	{
		subR->pf = 0;
		subRL->pf = 0;
		parents->pf = 0;
	}
	else if (pf == -1)
	{
		parents->pf = 0;
		subRL->pf = 0;
		subR->pf = -1;
	}
	else if(pf == 1)
	{
		subR->pf = 0;
		parents->pf = -1;
		subRL->pf = 0;
	}
	else
	{
		assert(false);
	}
}

注意细节是与2.2.3的左右双旋一致的,要提前保存几个结点.

1.3删除

对于删除来说,它的整体逻辑是和二叉搜索树的删除时大差不差的,唯一要注意的时更新平衡因子,以及不平衡时要进行旋转调整.

根据我们所规定的

平衡因子的大小等于 = 右子树的高度-左子树的高度

在这里如果我们在左子树删除结点相当于平衡因子--,在右子树删除结点相当于平衡因子++.

平衡因子的结束的条件也有所不同.

1.当平衡因子在更新完之后为-1或者1我们结束,因为在之前它一定时0,也就是左右高度时均衡的,我们删除操作并没有影响整颗二叉树的高度所以要结束.

2.当更新完平衡因子为0的情况要继续更新,因为更新前它一定是-1/1,对于父节点来说,它的左右高度差为1,符合avl树的要求,但是在我们删除之后,它为0平衡了,但是父节点整体的子树高度要发生变化了,所以要继续更新

3.当为-2/2的时候是不平衡了,我们删除破坏了avl树的结构.但具体调节的情况是和插入一致的.在这里不冗余介绍.

bool erase(const pair<K, V>& val)
{
	Node* cur = root;
	Node* parents = nullptr;
	while (cur)
	{
		if (cur->_kv.first < val.first)
		{
			parents = cur;
			cur = cur->right;
		}
		else if (cur->_kv.first > val.first)
		{
			parents = cur;
			cur = cur->left;
		}
		else
		{
			if (cur->left == nullptr)
			{
				if (cur == root)
				{
					root = cur->right;
				}
				else
				{
					if (parents->left == cur)
					{
						parents->left = cur->right;
					}
					else if (parents->right == cur)
					{
						parents->right = cur->right;
					}
				}
				delete cur;
				
			}
			else if (cur->right == nullptr)
			{
				if (cur == root)
				{
					root = cur->left;
				}
				else
				{
					if (parents->left == cur)
					{
						parents->left = cur->left;
					}
					else if (parents->right == cur)
					{
						parents->right = cur->left;
					}
				}
				delete cur;
			}
			else
			{
				Node* pminright = cur;
				Node* minright = cur->right;
				while (minright->left)
				{
					pminright = minright;
					minright = minright->left;
				}
				swap(cur->_kv, minright->_kv);
				if (pminright->left == minright)
					pminright->left = minright->right;
				else
					pminright->right = minright->right;
				delete minright;
				parents = pminright;
			}
			while (parents)
			{
				if (parents->left == nullptr)
				{
					parents->pf++;
				}
				else if(parents->right==nullptr)
				{
					parents->pf--;
				}
				if (parents->pf == 1 || parents->pf == -1)
				{
					break;
				}
				else if(parents->pf==0)
				{
					cur = parents;
					parents = parents->parents;
				}
				else if (parents->pf == -2 || parents->pf == 2)
				{
					if (parents->pf == 2 && cur->pf == 1)
					{
						RotateL(parents);
					}
					else if (parents->pf == -2 && cur->pf == -1)
					{
						RotateR(parents);
					}
					else if (parents->pf == 2 && cur->pf == -1)
					{
						RotateRL(parents);
					}
					else if (parents->pf == -2 && cur->pf == 1)
					{
						RotateLR(parents);
					}
					else
					{
						assert(false);
					}
					
					
				}
			}
			return true;
		}
	}
	return false;
}

在这里需要注意的是在左右孩子都有的情况进行删除我们走的并不是parents的逻辑,而是寻找了一个值进行替代,在删除结束后要将pminright的值给parents;

1.4查找

查找是与二叉搜索树一致的,找到就返回当前结点找不到就返回nullptr

Node* find(const pair<K, V>& val)
{
	Node* cur = root;
	while (cur)
	{
		if (cur->_kv.first < val.first)
		{
			cur = cur->right;
		}
		else if (cur->_kv.first > val.first)
		{
			cur = cur->left;
		}
		else
		{
			return cur;
		}
	}
	return nullptr;
}

1.5平衡因子检测

我们可以通过递归求高度差相减来求平衡因子是否正确

bool _IsBalanceTree(Node* root)
{
	// 空树也是AVL树
	if (nullptr == root)
		return true;

	// 计算pRoot结点的平衡因子：即pRoot左右子树的高度差
	int leftHeight = height(root->left);
	int rightHeight = height(root->right);
	int diff = rightHeight - leftHeight;

	// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
	// pRoot平衡因子的绝对值超过1，则一定不是AVL树
	if (abs(diff) >= 2)
	{
		cout << root->_kv.first << "高度差异常" << endl;
		return false;
	}

	if (root->pf != diff)
	{
		cout << root->_kv.first << "平衡因子异常" << endl;
		return false;
	}

	// pRoot的左和右如果都是AVL树，则该树一定是AVL树
	return _IsBalanceTree(root->left) && _IsBalanceTree(root->right);
}

测试案例

 AVLTree<int, int> t;
 // 常规的测试用例
 //int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
 // 特殊的带有双旋场景的测试用例
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
 for (auto e : a)
 {
     //fsfsfsfsf
     /* if (e == 14)
      {
          int x = 0;
      }*/
   
     t.insert({ e, e });
     /*cout << "Insert" << e << "->";
     cout << t.IsBalanceTree() << endl;*/
 }
 t.Inorder();
 cout << t.IsBalanceTree() << endl;
 t.erase({3,3});
 t.erase({ 6,6 });
 t.Inorder();
 cout << t.IsBalanceTree() << endl;

1.6其他

在这里还有size,height等函数的实现,但与二叉搜索树的是一致的,同时包括1.5的函数均用类封装提供接口的形式实现具体代码可以参考我的代码仓库
代码参考