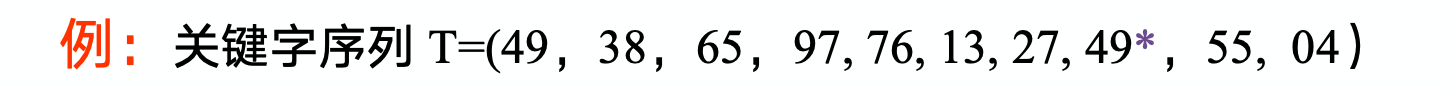要学的：

熟练掌握插入排序（直接插入排序、折半插入排序、希尔排序）、交换排序（冒泡排序、快速排序）、简单选择排序的算法实现及其性能分析

掌握希尔排序的方法及其性能分析

各种内部排序方法的比较（时间、空间、稳定性、选择原则）

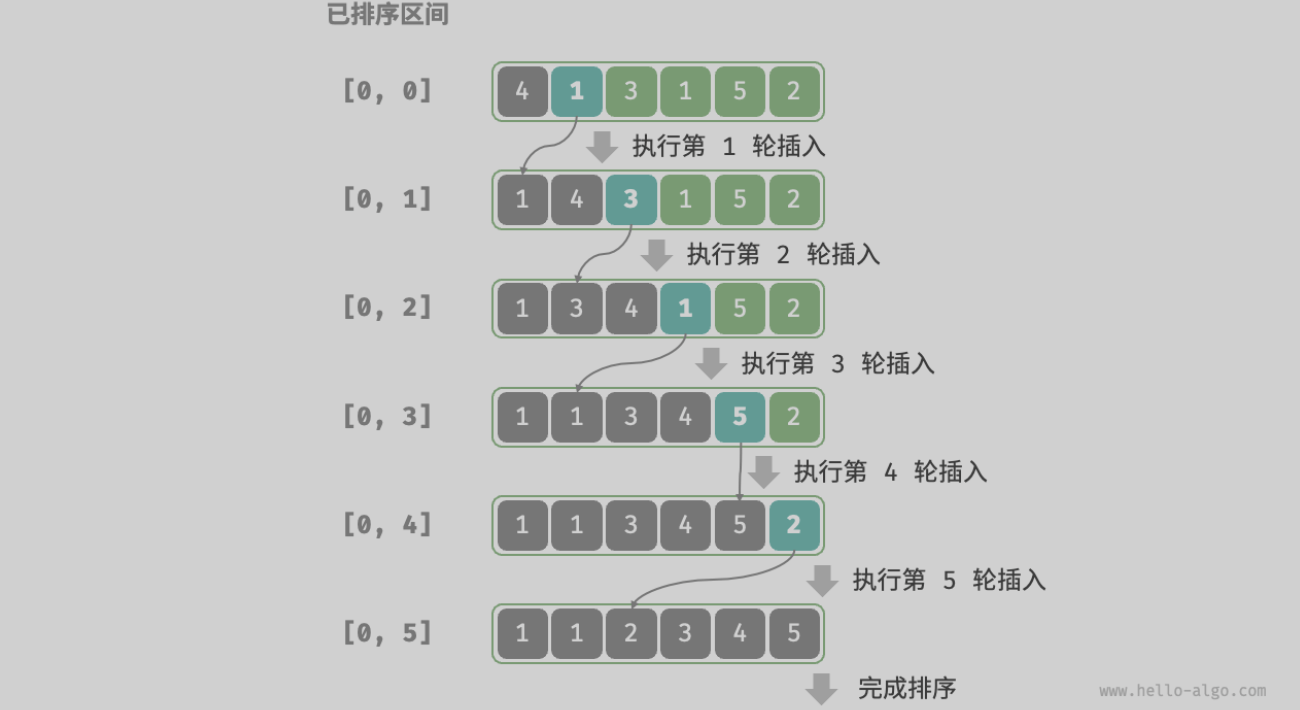
插入排序

直接插入排序(基于顺序查找)

工作原理类似理牌

在未排序区间选择一个基准元素，与其左侧已排序区间的元素逐一比较大小，找到要插入的正确位置
将该位置后面的元素依次向后移动一位 arr[j + 1] = arr[j]
再把元素赋给正确位置索引arr[ j + 1 ]

代码实现

c 复制代码

/* 插入排序 */
void insertionSort(int nums[], int length) {
    // 外循环：已排序区间为 [0, i-1]
    for (int i = 1; i < length; i++) {
        // 从未排序区间选取一个值作为基准
        int base = nums[i];
        //内循环：比较 base 与已排序区间中的元素
        int j = i - 1;
        //找到正确位置，将该位置后面的元素依次向后移动一位
        for(; j >= 0 && nums[j] > base; j--) {
            nums[j + 1] = nums[j];
        }
        // 将 base 赋值到正确位置
        nums[j + 1] = base;
    }
}

时间复杂度为 O(n^2)
空间复杂度为 O(1)
是一种稳定的排序方法
平均情况比较次数和移动次数为(n^2) / 4

最坏情况(输入数组是倒序)下，每次插入操作需要循环n-1，n-2，...，2，1次，求和得到(n−1)n/2，所以O(n^2)。

折半插入排序(基于折半查找)

步骤：

在未排序区间选择一个基准元素
先用折半查找找到要插入的正确位置区间[low,high]
从high+1开始，后面的元素向后移动一位
再把基准元素赋值给正确位置arr[ high+1 ]

代码实现

c 复制代码

void BInsertSort(int L[], int length)
{
    for (int i = 2; i <= length; ++i)
    {
        //折半查找找到要插入的正确位置区间[low,high]
        int base = L[i];
        int low = 1;
        int high = i - 1;
        while (low <= high)
        {
            int mid = (low + high) / 2;
            if (base < L[mid])
                high = mid - 1;
            else
                low = mid + 1;
        }
        //从high+1开始，后面的元素向后移动一位
        for (int j = i - 1; j >= high + 1; j--)
        {
            L[j + 1] = L[j];
        }
        //基准元素base赋值给正确位置arr[ high+1 ]
        L[high + 1] = base;
    }
}

性能分析

相较于直接插入排序，只是用折半查找减少了比较次数，但没有减少移动次数。

平均性能好于直接插入排序，但是最好情况性能弱于直接插入的最好情况

时间复杂度为 O(n^2)
空间复杂度为 O(1)
是一种稳定的排序方法

希尔排序(基于逐趟缩小增量)

本质还是直接插入排序，但是分多次

引入：直接插入排序在基本有序和待排序的元素较少时，效率较高

原理：

先将整个待排序列分割成若干子序列，分别进行直接插入排序
当每个子序列各自有序时，再对整个序列进行一次直接插入排序(也就是dk = 1)。

怎么分割子序列？

将相隔dk的记录组成一个子序列( dk逐趟缩短 )，直到dk＝1为止。

习题

	0	1	2	3	4	5	6	7	8	9
	49	38	65	97	76	13	27	49*	55	04
dk = 5	13	27	49*	55	04	49	38	65	97	76
dk = 3	13	04	49*	38	27	49	55	65	97	76
dk = 1	04	13	27	38	49*	49	55	65	76	97

对每个子序列进行直接插入排序，其实就相当于：

dk不为 1 的时候，把隔dk的两个值是否交换位置
dk = 1 的时候，把隔dk的值作为基准与前面已排序列一一比较，找到正确位置插入。

性能分析

时间复杂度是n和d的函数：
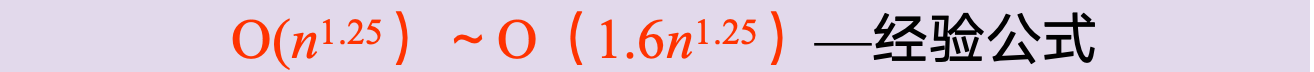
空间复杂度为 O(1)
是一种不稳定的排序方法
最后一个增量值必须为1
不宜在链式存储结构上实现
适合初始记录无序，n较大

习题

设待排序的关键字序列为{12，2，16，30，28，10，16*，20，6，18}，试写出使用希尔排序（增量选取5，3，1）排序方法，每趟排序结束后关键字序列的状态。

	1	2	3	4	5	6	7	8	9	10
	12	2	16	30	28	10	16*	20	6	18
dk = 5	10	2	16	6	18	12	16*	20	30	28
dk = 3	6	2	12	10	18	16	16*	20	30	28
dk = 1	2	6	10	12	16	16*	18	20	28	30

交换排序

下面都以从小到大序列为例

冒泡排序

内层循环：从头遍历，两两比较，较大的数放在后面，即交换位置，直到最大的数在最末尾。
外层循环：像这样遍历 length - 1 遍。

length - 1 怎么来的？

比如1，2排序，外循环只需遍历一遍，也就是length-1遍

代码实现

c 复制代码

/* 冒泡排序 */
void bubbleSort(int nums[], int length) {
    // 外循环：数组几个数就需要进行i轮冒泡
    for (int i = 0; i < length; i++) {
        // 内循环：
        // 每轮冒泡
        // 数组长度减去第i轮，因为每轮冒泡都会将最大的数冒泡到最后面，所以不需要再比较后面的数
        // length - 1是因为要防止数组越界，因为要比较 nums[j] > nums[j + 1]
        for (int j = 0; j < length- 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                int temp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = temp;
            }
        }
    }
}

用标志位记录交换，优化后的冒泡排序：

c 复制代码

/*优化后的冒泡排序*/
void bubbleSort2(int nums[], int length) {
    // 外循环：数组几个数就需要进行i轮冒泡
    for (int i = 0; i < length; i++) {
        //每轮冒泡开始前，标志位isSwap置为false
        bool isSwap = false;
        // 内循环：
        // 每轮冒泡
        // 数组长度减去第i轮，因为每轮冒泡都会将最大的数冒泡到最后面，所以不需要再比较后面的数
        // length - 1是因为要防止数组越界，因为要比较 nums[j] > nums[j + 1]
        for (int j = 0; j < length- 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                int temp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = temp;
                //每次交换后，isSwap置为true
                isSwap = true;
            }
        }
        //如果本轮没有发生交换，说明已经排序好了，即刻退出循环
        if(!isSwap)break;
    }
}

性能分析

最好情况：输入序列是顺序，只需 1趟排序，比较 n-1 次，不移动

最坏情况：输入序列是逆序，需 n 趟排序，第i趟比较 n -1 -i 次，移动3(n -1 -i)次

复制代码

总比较次数：

复制代码

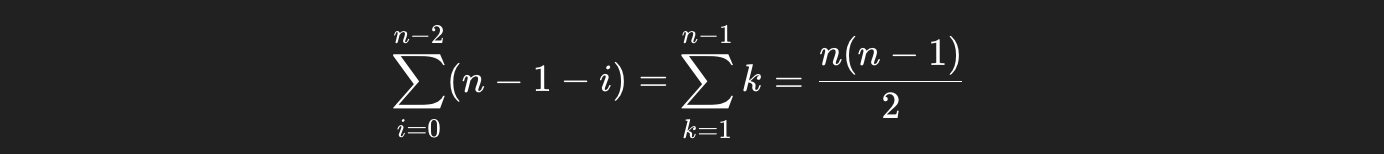
总移动次数：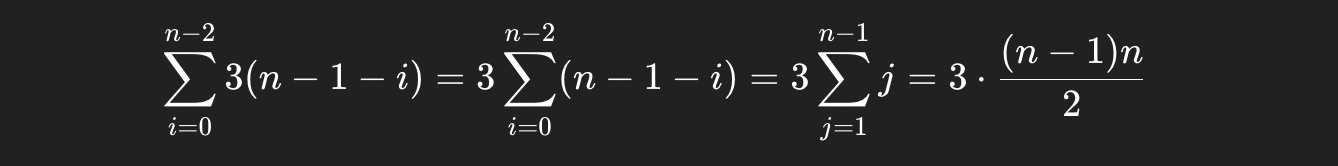

习题

对n个不同的元素进行冒泡排序，在元素无序的情况下比较的次数最多为（）。

A．n+1 B．n C．n-1 D．n(n-1)/2

选D

快速排序

步骤：

首先，对原数组执行一次"哨兵划分"，得到未排序的左子数组和右子数组。
然后，对左子数组和右子数组分别递归执行"哨兵划分"。
持续递归，直至子数组长度为 1 时终止，从而完成整个数组的排序。

哨兵划分：先把输入序列分成两个部分，左 <= 基准 <= 右

复制代码

1. arr[ left ] 作为基准
  2. 从arr[ right ] 出发，从右向左 和 基准比较，找到首个 大于 基准数的元素arr[ j ]
  3. 从arr[ left ] 出发，从左向右 和 基准比较，找到首个 小于 基准数的元素arr[ i ]
  4. 交换arr[ i ]和arr[ j ]
  5. 重复步骤2，直到两个子数组的分界线，把分界线处的元素arr[ i ]和arr[ left ]交换

得到如下形式：左 <= 基准 <= 右

左子数组	基准数	右子数组

左子数组任意元素 ≤ 基准数 ≤ 右子数组任意元素

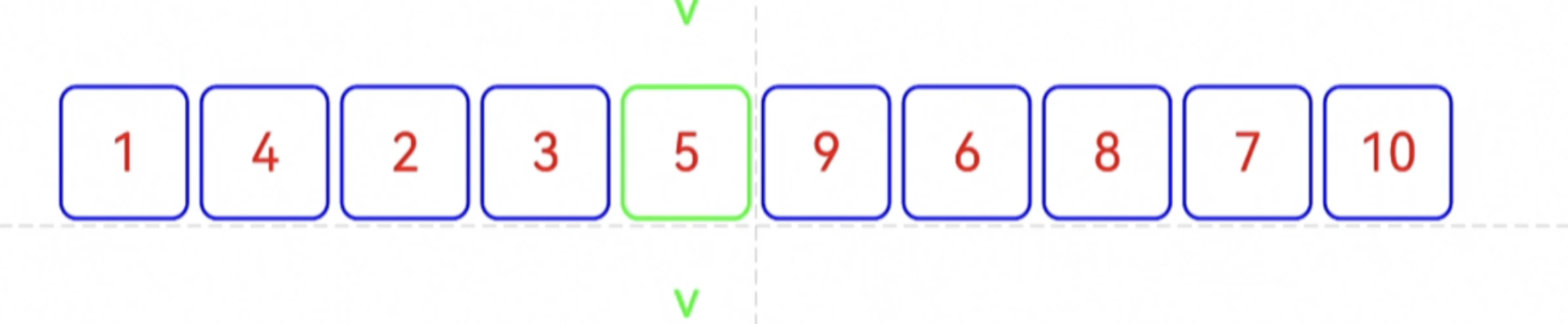
哨兵划分的代码实现

c 复制代码

/* 元素交换 */
void swap(int nums[], int i, int j) {
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

/* 哨兵划分 */
int partition(int nums[], int left, int right) {
    // 以 nums[left] 为基准数
    int i = left, j = right;
    while (i < j) {
        while (i < j && nums[j] >= nums[left]) {
            j--; // 从右向左找首个小于基准数的元素
        }
        while (i < j && nums[i] <= nums[left]) {
            i++; // 从左向右找首个大于基准数的元素
        }
        // 交换这两个元素
        swap(nums, i, j);
    }
    // 将基准数交换至两子数组的分界线
    swap(nums, i, left);
    // 返回基准数的索引
    return i;
}

递归上面的哨兵划分的代码实现

c 复制代码

/* 快速排序 */
void quickSort(int nums[], int left, int right) {
    // 子数组长度为 1 时终止递归
    if (left >= right) {
        return;
    }
    // 哨兵划分
    int pivot = partition(nums, left, right);
    // 递归左子数组、右子数组
    quickSort(nums, left, pivot - 1);
    quickSort(nums, pivot + 1, right);
}

习题1

每一趟：

	0	1	2	3	4	5	6	7	8
		49	38	65	97	76	13	27	49
第一趟	49		38	65	97	76	13	27	49
	49	27	38	13		76	97	65	49
		27	38	13	49	76	97	65	49
第二趟	27		38	13
	27	13		38
		13	27	38
	76						97	65	49
	76					49	65		97
						49	65	76	97
		13	27	38	49	49	65	76	97

每一步详解：

arr[ left ] 作为基准放在0处
从arr[ right ]开始向左一直找，直至找到首次小于基准的数，放在arr[ left ]空出来的1处
再从2处开始向右一直找，直至找到首次大于基准的数，放在步骤2空出来的位置处
一直重复上述步骤2和3，直到左右遍历指向同一个索引，把基准arr[ left ]放到这个位置
这时，构造出一个[左子数组，基准数，右子数组]的数组
分别对左右子数组进行步骤123，也就是哨兵划分递归
得到最终的有序序列

做题的话就按这个步骤就行，好理解
习题2

	0	1	2	3	4	5	6
		46	79	56	38	40	84
第一次划分	46		79	56	38	40	84
	46	40	38		56	79	84
		40	38	46	56	79	84

选C

性能分析

时间复杂度为 O(nlog⁡n)
空间复杂度为 O(n)
非稳定排序
平均计算时间是O( nlog2(n) )

对于平均计算时间来说，上述排序中快速排序是效率最高的

不过快速排序在某些输入下的时间效率可能降低，比如输入数组是完全倒序的，这时候的快速排序又变成了效率最低的起泡排序。

优化快速排序------基准数优化

在数组中选取三个候选元素（通常为数组的首、尾、中点元素）， 并将这三个候选元素的中位数作为基准数 。

选择排序

简单选择排序

原理

一共 length-1 轮排序

每轮在区间 [0,length-1 -n] 中找到最大值，放在末位arr[ length-1 -n ]处

或者

每轮在区间 [n,length−1] 中找到最小值，放在首位arr[ n ]处

n是当前的轮数，n从0到length-1

步骤

下面以找最小值的方法为例：

初始状态下，所有元素未排序，即未排序（索引）区间为 [0,length−1] 。
选取区间 [0,length−1] 中的最小元素，将其与索引 0 处的元素交换。完成后，数组前 1 个元素已排序。
选取区间 [1,length−1] 中的最小元素，将其与索引 1 处的元素交换。完成后，数组前 2 个元素已排序。
以此类推，每轮选取区间 [n,length−1] 中的最小元素。经过 n−1 轮选择与交换后，数组前 n−1 个元素已排序。
仅剩的一个元素必定是最大元素，无须排序，因此数组排序完成。

代码实现：

c 复制代码

/* 选择排序 */
void selectionSort(int nums[], int length) {
    // 外循环：n轮
    for (int n = 0; n < length - 1; n++) {
        // 内循环：找到未排序区间内的最小元素
        int minIndex = n;
        for (int j = n + 1; j < length; j++) {
            if (nums[j] < nums[minIndex])
                minIndex = j; // 记录最小元素的索引
        }
        // 将该最小元素与未排序区间的首个元素交换
        int temp = nums[minIndex];
        nums[minIndex] = nums[n];
        nums[n] = temp;
    }
}

性能分析

时间复杂度为 O(n^2)

空间复杂度为 O(1)

非稳定排序(如果要实现稳定的话，元素应该逐个向后移动)

排序

插入排序

直接插入排序(基于顺序查找)

代码实现

折半插入排序(基于折半查找)

代码实现

性能分析

希尔排序(基于逐趟缩小增量)

性能分析

交换排序

冒泡排序

代码实现

性能分析

快速排序

步骤：

哨兵划分的代码实现

递归上面的哨兵划分的代码实现

性能分析

优化快速排序------基准数优化

选择排序

简单选择排序

原理

步骤

代码实现：

性能分析

所有排序的总结