从零开始理解FlashAttention：算法细节图解

🧠 向所有学习者致敬！

"学习不是装满一桶水，而是点燃一把火。" ------ 叶芝

我的博客主页： https://lizheng.blog.csdn.net

🌐 欢迎点击加入AI人工智能社区！

🚀 让我们一起努力，共创AI未来！ 🚀

注意力机制无疑是现代深度学习架构中最重要的构建模块之一。它被广泛应用于各种任务的最先进模型中，从自然语言处理（NLP）到计算机视觉。然而，注意力机制也是这些模型中最昂贵的操作之一。因此，自然而然地，大量研究致力于让它变得更快、更节省内存。而这些研究大多基于对注意力机制的近似，这可能会导致精度损失。

在从零开始理解FlashAttention系列的第二部分中，我们将深入探讨FlashAttention的细节，看看它是如何实现7.6倍的巨大加速，以及如何在计算精确注意力分数的同时实现 O ( N ) O(N) O(N) 的内存复杂度。

🚀 那么，让我们马上开始吧！

好的呀！那我就开始啦！以下是翻译后的文档内容：

这是多部分系列文章从零开始理解FlashAttentio 的第 2 部分。

注意力机制无疑是现代深度学习架构中最重要的构建块之一。它被用于各种任务的最先进的模型中，从自然语言处理到计算机视觉都有它的身影。然而，注意力机制也是这些模型中最昂贵的操作之一。所以，很自然地，有很多研究致力于让它变得更快、更节省内存。大部分研究都是基于对注意力机制进行近似，但这可能会导致精度损失。

在从零开始理解FlashAttentio的第 2 部分，我们将深入探讨 FlashAttention 的细节，看看它是如何实现高达 7.6 倍的速度提升，以及如何在仍然计算精确注意力分数的同时，达到 O(N) 的内存复杂度。

🚀 那我们马上开始吧！

1. 第 1 部分的内容回顾

在本系列的第一部分，我们为理解 FlashAttention 论文奠定了基础。

我们对注意力机制有了基本的直觉，了解了它是如何工作的，以及它在模型中的位置。我们还简要讨论了现代 GPU、CUDA 编程模型以及 GPU 的内存层次结构。

接着，我们转向研究 GPU 上两个矩阵是如何相乘的，以及我们如何通过利用 GPU 的内存层次结构（共享内存 ）、在单个线程中计算多个结果（块分块 ）以及将多个内核融合成一个内核（内核融合）来优化这个过程。

最后，我们得到了下面这张图，它展示了我们在注意力机制上的主要问题：我们需要读取和写入巨大的 NxN 矩阵作为中间结果，这不仅耗时，还需要大量内存。

图 1：注意力层中每个内核的读取和写入操作。

我们最终搞清楚了什么阻止了我们将优化矩阵乘法时使用的技术应用到注意力机制上：

SoftMax 操作阻止了我们融合内核，因为它是在整个向量 x 上操作的，而不是在向量的块上操作，
而且我们需要在反向传播中使用这些中间结果来计算梯度。

理解这两点可真是费了不少功夫，如果你坚持到这里，那可真是太棒了！🎉

现在，让我们保持这股劲头，继续深入探索：用 FlashAttention 解决这些问题！

2. FlashAttention

论文的标题 "FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness" 很具体，已经告诉我们它解决了哪些问题：

快速：执行时间大幅减少。注意力层本身的速度提升了 7.6 倍，从头开始训练 GPT-2 的速度提升了 3.5 倍。
节省内存 ：内存使用大幅减少，让我们可以训练更大的模型、更大的上下文窗口和更大的批次。因为标准注意力是 O(N²) 的内存复杂度，而 FlashAttention 是 O(N) 的。
精确注意力 ：与其他通过近似注意力机制的部分来实现加速和减少内存需求的方法（如 Linformer、Performers 或 Reformer）不同，FlashAttention 在计算精确注意力分数的同时实现了减少。
IO 意识：FlashAttention 利用现代 GPU 的内存层次结构来优化不同内存层级之间的数据传输。这是通过使用共享内存来存储中间结果，并且只将最终结果写入全局内存来实现的。

将这些改进可视化后，看起来就像这样：

图 2：FlashAttention 与之前方法的改进对比。

虽然这些听起来对很多人来说还很抽象，但让我们明确一下它能让我们做什么：

更快地训练相同的模型，
在更大的批次上训练相同的模型，
以相同的成本训练更大（可能性能更好的）模型，
训练具有更大上下文窗口的模型，
在更小的 GPU 上训练模型。

例如，在 8 块 A100 上训练 GPT-2 小模型，从 9.5 天缩短到了 2.7 天；GPT-2 中模型从 21.0 天缩短到了 6.9 天（使用 OpenWebText 数据集）。

❓那我们究竟是如何达到这一点的，我们需要解决哪些问题呢？

让我们来一探究竟！

2.1.我们需要解决的问题是什么？

正如我们在第 1 部分学到的，我们面临的主要问题是，我们需要读取和写入巨大的 NxN 矩阵作为中间结果，这不仅耗时，还需要大量内存。理想情况下，如果我们能够将 SoftMax 内核与矩阵乘法内核融合，并且只将最终结果写入全局内存，那该多好呀。

但是，我们遇到了两个问题，阻止了我们这么做：

图 3：阻止我们在注意力层中融合内核的两个问题。

我们先从第一个问题说起：SoftMax 操作。

2.2. 修复 SoftMax

回想一下我们在第 1 部分中提到的，为了乘以两个矩阵，我们利用了共享内存。输入被分成更小的块，结果被累加起来以获得最终结果：

图 4：矩阵乘法中共享内存的使用。

如果我们想将 SoftMax 内核与矩阵乘法内核融合，我们也必须将输入分成块，并且以某种方式将它们结合起来以获得最终结果。这就是 SoftMax 操作的分解发挥作用的地方。

我们先假设我们能够访问到计算 SoftMax 所需的所有值，并且也将 SoftMax 的定义转换成更接近论文中使用的那种形式：

图 5：SoftMax 方程。

到目前为止，这仅仅是重新表述了标准的 SoftMax 定义。

❗接下来可能是这个系列中最重要的部分啦： 我们将看到如何分解 SoftMax 操作，以便它可以一次应用于单独的块，这将允许我们将 SoftMax 内核与矩阵乘法内核融合，因为它们将操作相同的数据。

与其使用一个完整的向量 x 来计算 SoftMax，我们实际上在共享内存中只有 x 的一半可用。

图 6：分解的 SoftMax 操作可用的数据。

说清楚一点：我们不能简单地为 x 的第一部分计算 SoftMax，然后再为第二部分计算 SoftMax，因为我们需要知道整个向量 x 的最大值，才能计算数值稳定的 SoftMax。

相反，我们将采取以下方法：我们跟踪一些额外的指标，然后在每次迭代中，我们为当前块的 x 计算 SoftMax，将当前迭代的结果与之前的迭代结果结合起来，更新指标，然后相应地更新输出。

如果你还不明白，别担心！我们会详细讲解。

首先，让我展示一下将 SoftMax 操作应用于向量 x 的两个块时的新方程：

图 7：分解的 SoftMax 函数的方程。

我知道这看起来很复杂。但如果你做数学运算并代入值，你会看到这与我们之前看到的标准 SoftMax 表达式是等价的。为了说明这一点，我深入研究并为你做了这个练习，用于 l(x)：

图 8：展示分解的 SoftMax 函数与标准 SoftMax 函数的等价性。

❓但我们从中学到了什么呢？

关键的见解是，我们现在可以为 x 的第一块计算 SoftMax，然后为第二块计算 SoftMax（这两次计算相对于整个向量 x 来说都是不正确的），重新缩放中间结果，然后将它们结合起来以获得最终且有效的 x 的 SoftMax。如果你仔细观察，函数 m(x) 和 l(x) 是那些需要知道 x 中所有值的。因此，我们在全局内存中跟踪它们，并在每次迭代中逐步更新它们。我们这样做的原因有两个：

我们需要它们来更新和重新缩放后续迭代中的中间结果。
我们不想在反向传播时重新计算它们，以计算梯度。

好的，这仍然有点抽象。而且，我们还一直在谈论迭代......所以，是时候更具体一点，展示一下 FlashAttention 的前向传播的实际算法啦。

2.3 前向传播

在深入细节之前，我觉得先看看前向传播的高级执行过程是有意义的，并说明我们是如何迭代数据的。这已经可以让我们理解算法的大部分内容啦。

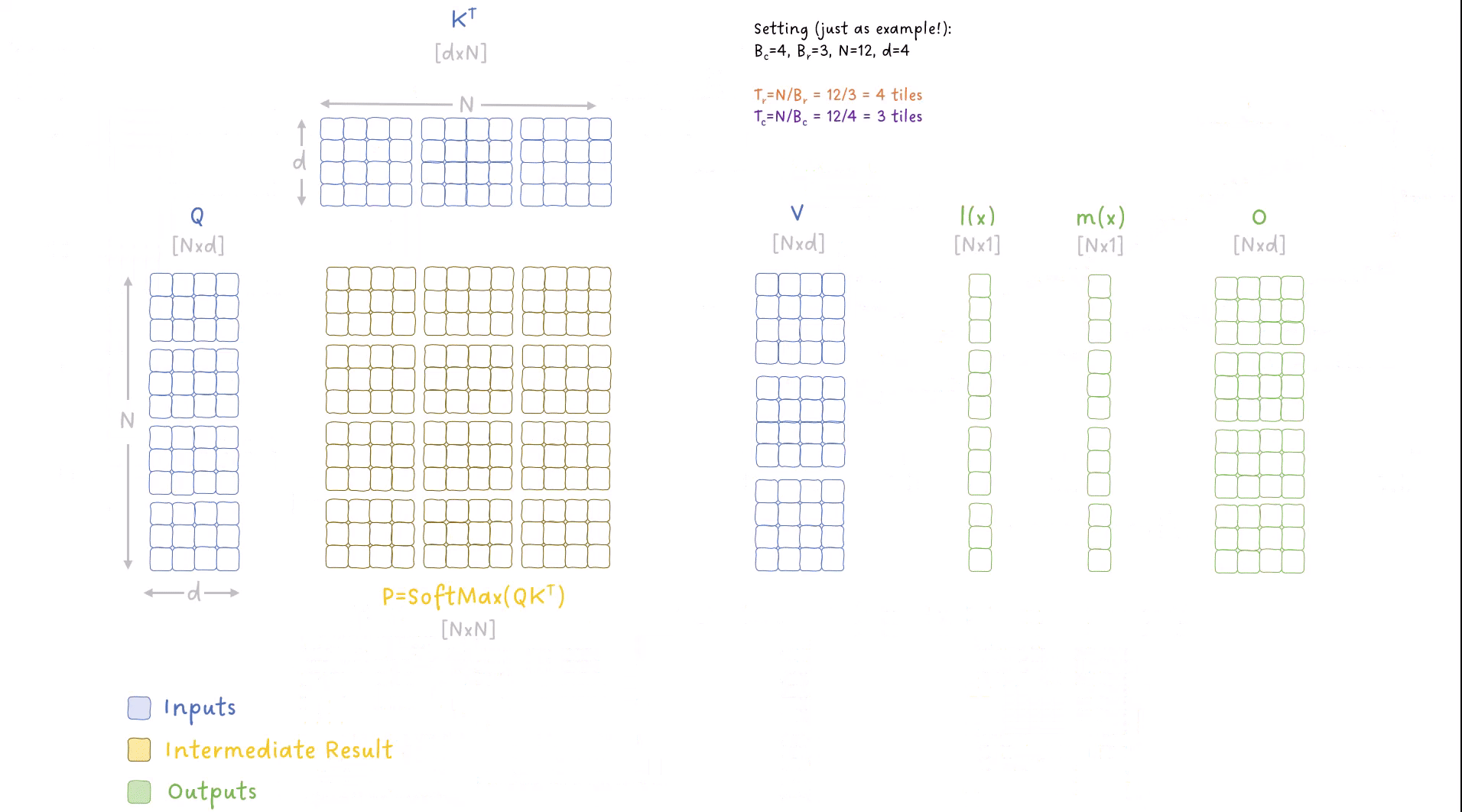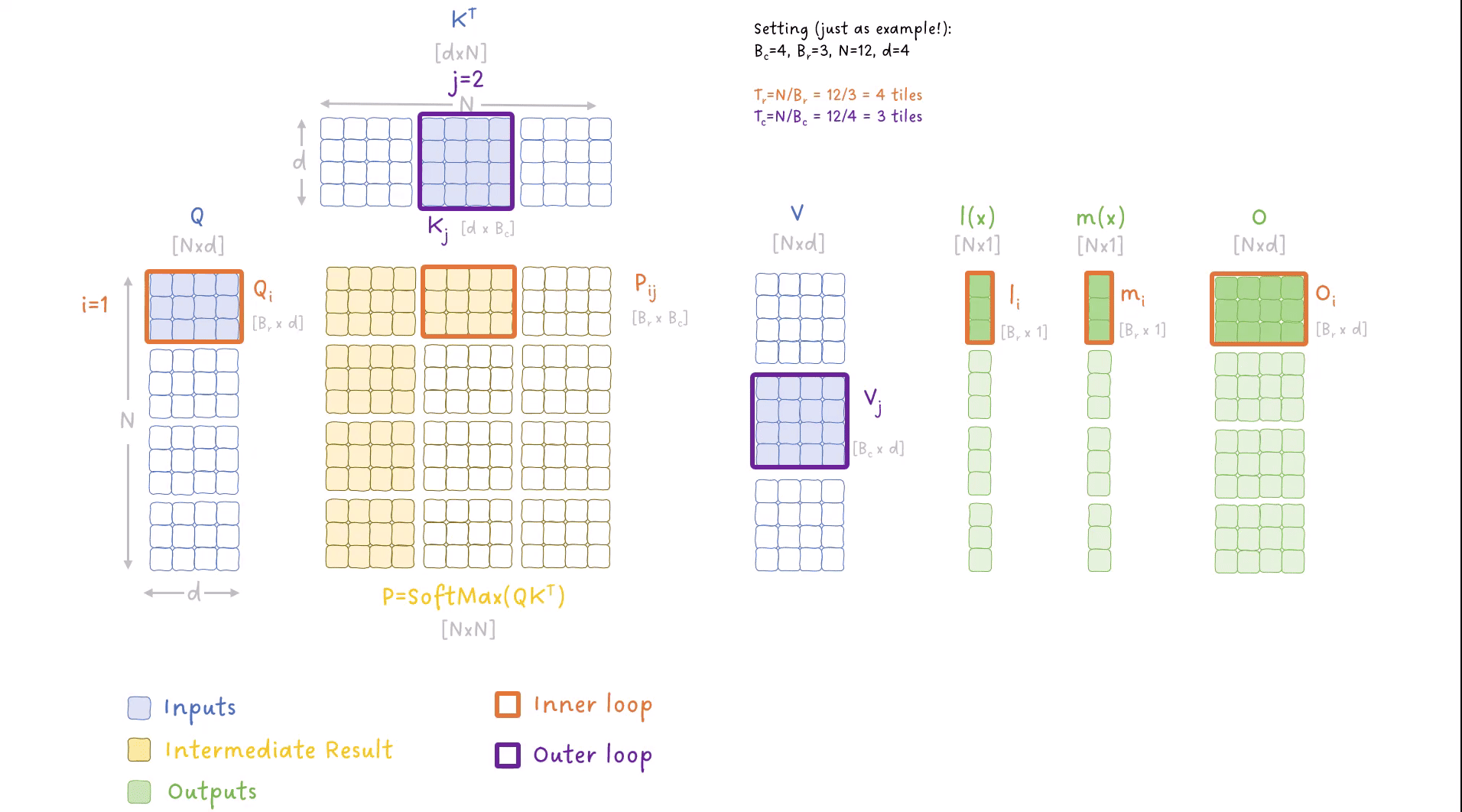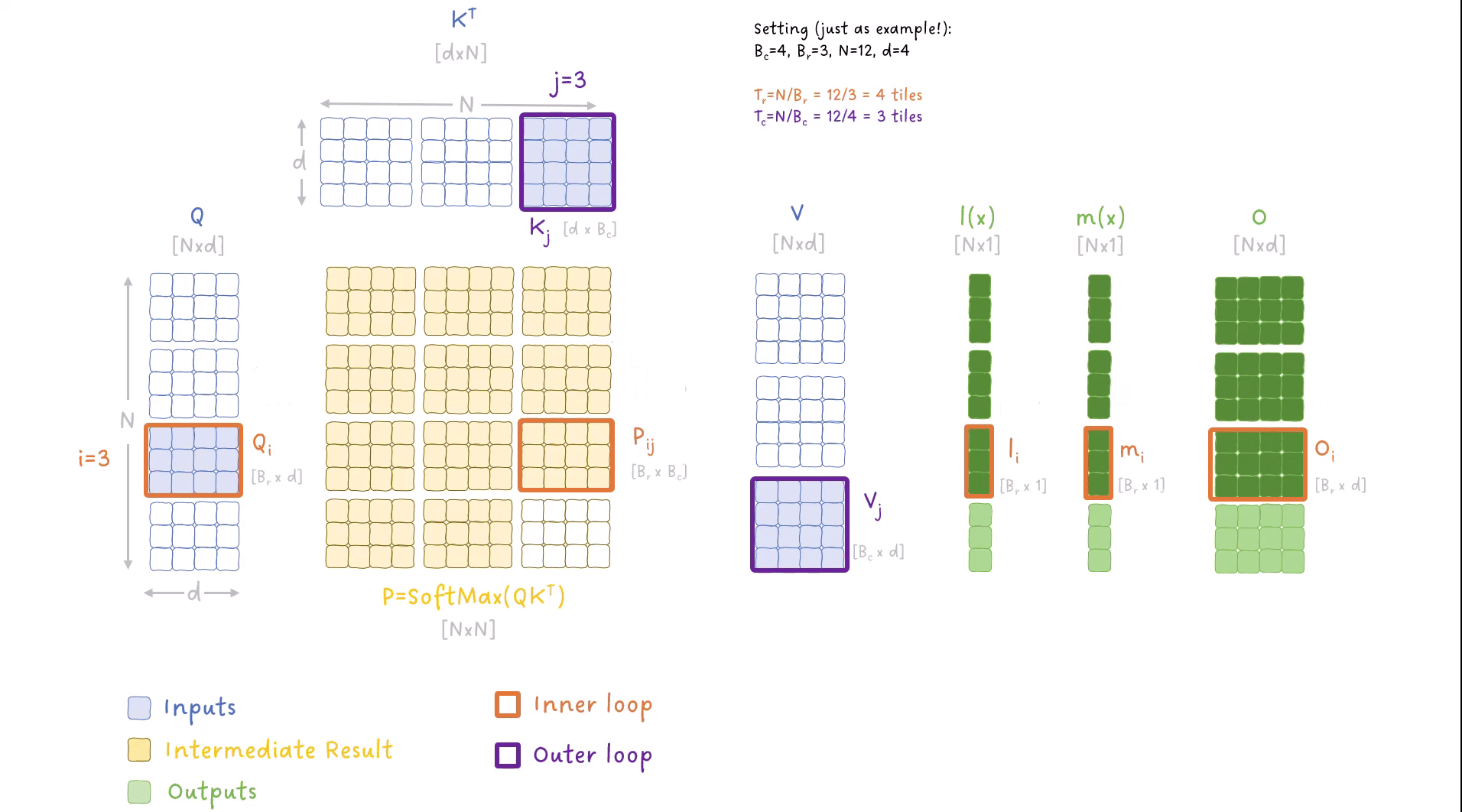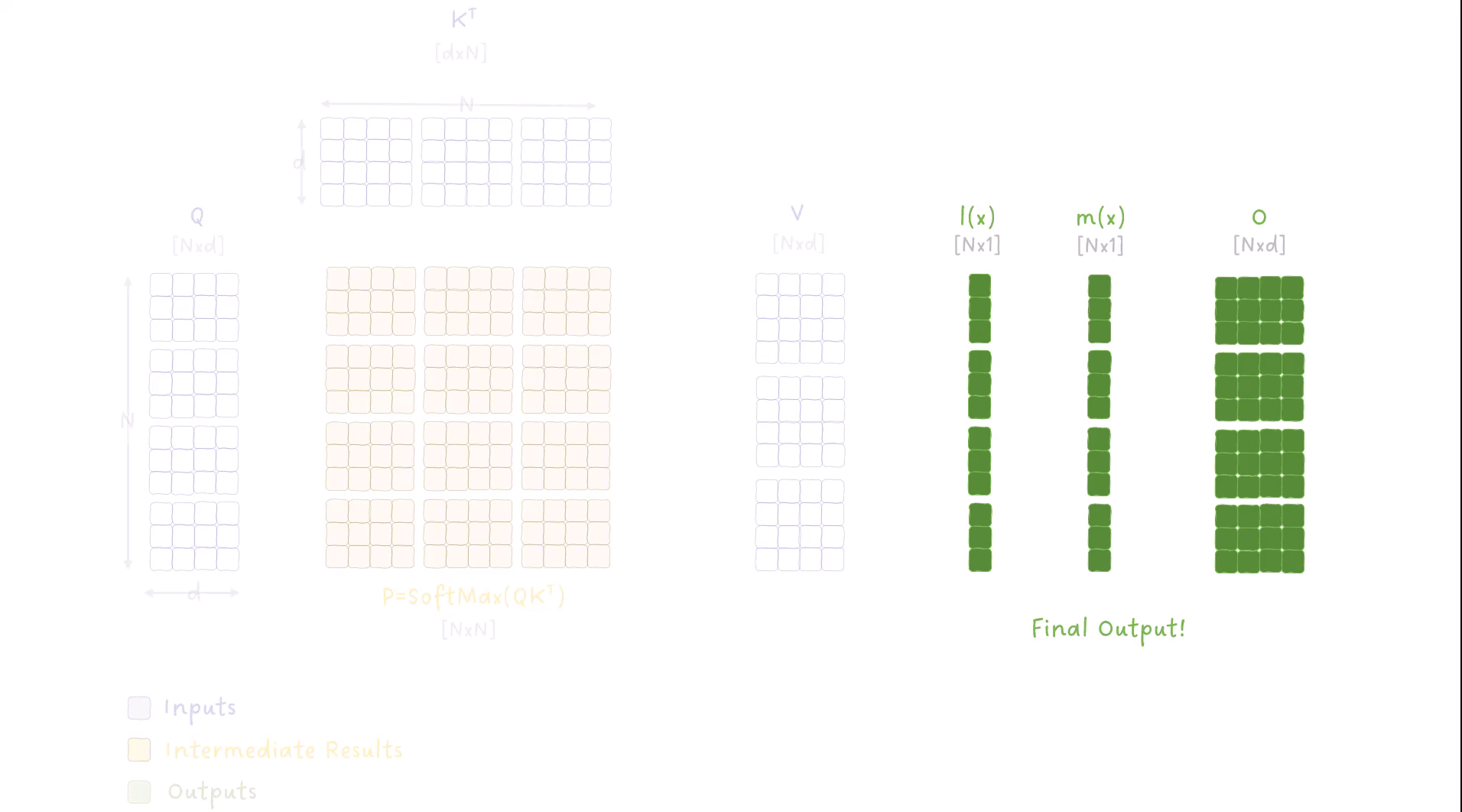
图 9：FlashAttention 算法中外循环和内循环迭代数据的动画。

这个动画里有很多东西（抱歉啦，我也是没办法 😅），所以你应该明白以下几点：

我们有两个循环来处理输入：
- 一个外循环，迭代 K 和 V 的块，索引为 j
- 一个内循环，迭代 Q 的块，索引为 i
我们多次迭代输出矩阵 O，在每次外循环迭代中更新其值。
我们还跟踪并逐步更新 SoftMax 计算中的指标 m(x) 和 l(x)。
我们不需要将 NxN 矩阵写入全局内存，而是将它们的小块保留在共享内存中，并且只将最终结果写入全局内存。
每个块包含多行，对应多个标记，因此我们并行计算多个 SoftMax 操作。

理解这个动画意味着你已经掌握了算法的核心，可能你已经开始明白它是如何节省时间和内存的啦。虽然对有些人来说这可能已经足够了，但我认为深入探究一下正在发生的事情是值得的。

我们继续来看看那些块状的中间结果，了解我们如何为它们计算 SoftMax。

图 10：SoftMax 如何应用于数据块。

虽然内循环迭代索引为 i 的行，但外循环迭代索引为 j 的列。回想一下，SoftMax 是针对每一行（代表输入序列中的一个单独标记）计算的。因此，如果我们处理一个数据块，我们需要同时计算多个 SoftMax 操作。此外，随着我们在外循环中向前推进，我们需要将当前块 x(2) 的 SoftMax 与之前块 x(1) 的 SoftMax 结合起来。

有了这些知识，我们终于可以看看 FlashAttention 论文中呈现的实际算法啦（我们稍后会详细讨论初始化和迭代更新）：

图 11：FlashAttention 前向传播算法。

试着将算法与上面的动画对应起来。同时，要明白这个算法融合了两个矩阵乘法内核和 SoftMax 内核，并且没有将 NxN 矩阵写入全局内存（即 HBM）。

你现在可能会问：如果我们没有中间结果，那我们该如何计算反向传播中的梯度呢？我们稍后会讨论这个问题。但首先，我们先完成前向传播。

我们来仔细看看步骤 6--11，我们在其中为当前块的 x 计算 SoftMax，并相应地更新指标 m(x) 和 l(x)。

此时，我们已经计算了 Q 和 K 的矩阵乘法，当前块的指标 m(x) 和 l(x)，并将它们与之前块的指标结合起来，以获得更新后的指标。

现在我们可以使用当前块的 x 和更新后的指标来更新输出矩阵 O 。这是在步骤 12 中完成的。这一步有点棘手，因为它已经融合了 P 和 V 的矩阵乘法内核与 SoftMax 内核。所以，让我们详细看看这一步：

图 12：解释 FlashAttention 算法内循环中的输出方程。

diag（向量）构造一个矩阵，该向量在对角线上，其余位置为零。这是一种技巧，用于将矩阵的每一行与向量中的对应值相乘。我们这样做是因为我们分别计算每个块的 SoftMax，因为这些对应于单独的标记。

再次强调，这种递归更新与融合内核相结合，确实很难理解 😅。但如果你代入值并进行数学运算，你会发现一切都很完美地结合在一起。

我们还没有涵盖的是算法中步骤 2 的初始化，即指标 m(x) 和 l(x) 以及输出矩阵 O 的初始化。

由于 O 、m(x) 和 l(x) 的更新是递归进行的（即我们重复使用之前迭代的结果），我们需要考虑一个基本情况，以防我们没有之前的迭代。因此，我们将 O 和 l(x) 初始化为零，将 m(x) 初始化为负无穷大。如果你进行数学运算并将初始值代入分解的 SoftMax 方程，你会发现我们得到了应用于 x 的第一块的标准 SoftMax 操作。

图 13：输出为何以这种方式初始化。

剩下的就是运行整个算法并输出最终的 Nxd 矩阵 O。这就是前向传播！🎉恭喜你还坚持到了这里！

接下来，让我们讲讲通常在大多数博客文章中被忽视的部分：反向传播。这里就是我们计算梯度并更新模型参数的地方。

你知道吗？FlashAttention 的作者 Tri Dao 还参与了 Mamba 状态空间模型的研究。这是一种用于序列建模的替代 Transformer 的方法，可以将计算复杂度从 O(N²) 降低。如果你想了解更多，可以看看我关于它的系列文章哦。

2.4 反向传播

通常，反向传播并不是什么大不了的事，那我们为什么还要在这里讲呢？原因有两个：

我们缺少前向传播中用于计算梯度的中间结果，因为我们为了节省内存和时间而没有保存它们。
在反向传播中，我们也有和前向传播一样的问题：我们不希望生成巨大的 NxN 矩阵。所以，我们仍然需要一个在共享内存上操作的融合内核。

不过好消息是，反向传播的算法与前向传播非常相似，我们分别在外循环和内循环中迭代相同的数据块。

那么，那些丢失的中间结果怎么办呢？其实，我们可以在反向传播中重新计算它们。记住，我们的 GPU 核心比从全局内存读取和写入数据的速度快得多。所以即使我们像在前向传播中那样低效地重新计算相同的中间结果，我们也比将它们写入全局内存要快。

实际上，我们不需要重新计算所有内容：还记得我们把指标 m(x) 和 l(x) 保留在全局内存中吗？现在我们可以利用它们来计算当前块的 x 的 SoftMax，并且这次从一开始就计算正确！

在跳到算法之前，我们先试着理解一下我们需要计算什么。

图 14：比较注意力层的前向传播和反向传播。

我们需要计算损失相对于模型参数的梯度。这是通过应用链式法则来完成的，一次计算一个梯度，直到我们得到相对于输入矩阵 Q 、K 和 V 的损失梯度。所以，就像我的教授过去常说的那样："这只是练习，不是惩罚"，让我们写下这些方程。

正如我们在后面将要看到的，这些方程中有一些需要注意的地方，我会明确指出：

计算 SoftMax 操作的梯度时，我们需要格外小心，因为 SoftMax 是按行计算的，而不是针对整个矩阵。这意味着我们需要分别计算输出矩阵 O 每一行的梯度！
术语可能会有点令人困惑，因为损失 L 相对于某个其他值（比如 V ）的梯度表示为 𝜕L/𝜕V ，并且用 dV 表示。
最后，我们仍然需要考虑分块迭代。

但，我们先从"简单"的开始，应用链式法则，看看我们需要计算哪些项。回想一下，我们感兴趣的是 dV 、dK 和 dQ。

图 15：在注意力层的反向传播中应用链式法则计算梯度。

现在，让我们逐层计算这些梯度。我们先从 O=PV 的矩阵乘法开始。

图 16：反向传播通过注意力层的第一步：P 和 V 的乘法。

通过这一步，我们已经计算出了我们感兴趣的第一个梯度：dV 。可能最复杂的部分是理解如何对矩阵求导，尤其是转置是从哪里来的，为什么 dO 要么从左边乘，要么从右边乘。如果你扩展了表达式，并计算了相对于矩阵每个元素的导数，你就会明白转置是从哪里来的。作为一个经验法则，如果相对于第一个矩阵求导，上游梯度 dO （这是数学上的花哨说法，表示相对于输出矩阵 O 的损失梯度）从左边乘；如果相对于第二个矩阵求导，从右边乘。

计算 dK 和 dQ 需要我们通过 SoftMax 和 Q 与 K 的矩阵乘法进行反向传播。我们继续来看 SoftMax。回想一下，SoftMax 是针对每一行 i 计算的，而不是针对整个矩阵。按照索引的表示，i: 表示第 i 行的所有列 j。

图 17：反向传播通过注意力层的第二步：SoftMax 操作。

通过一些代数技巧，我们得到了单行的梯度 dS ，并且通过计算所有行并将它们堆叠在一起，我们最终得到了 dS 。有了 dS ，我们现在可以计算相对于 Q 和 K 的矩阵乘法的梯度，以得到我们缺失的感兴趣梯度：dK 和 dQ。

图 18：反向传播通过注意力层的第三步：得到 dQ 和 dK。

就这样，我们已经计算出了注意力机制的所有梯度 dQ 、dK 和 dV，然后可以进一步向后传播并更新模型参数啦。

在查看论文中的实际算法之前，我们需要再讲最后一个内容：我们需要考虑分块和共享内存上的迭代，因为每次我们只有访问数据小块的权限。所以，在内循环的每次迭代中，我们需要重新计算中间结果。好消息是，我们已经将指标 m(x) 和 l(x) 保留在全局内存中，所以我们可以利用它们来计算当前块的 x 的 SoftMax，而不需要再次逐步更新。