趣味编程：四叶草

概述：在万千三叶草中寻觅，只为那一抹独特的四叶草之绿，它象征着幸运与希望。本篇博客主要介绍四叶草的绘制。

1. 效果展示

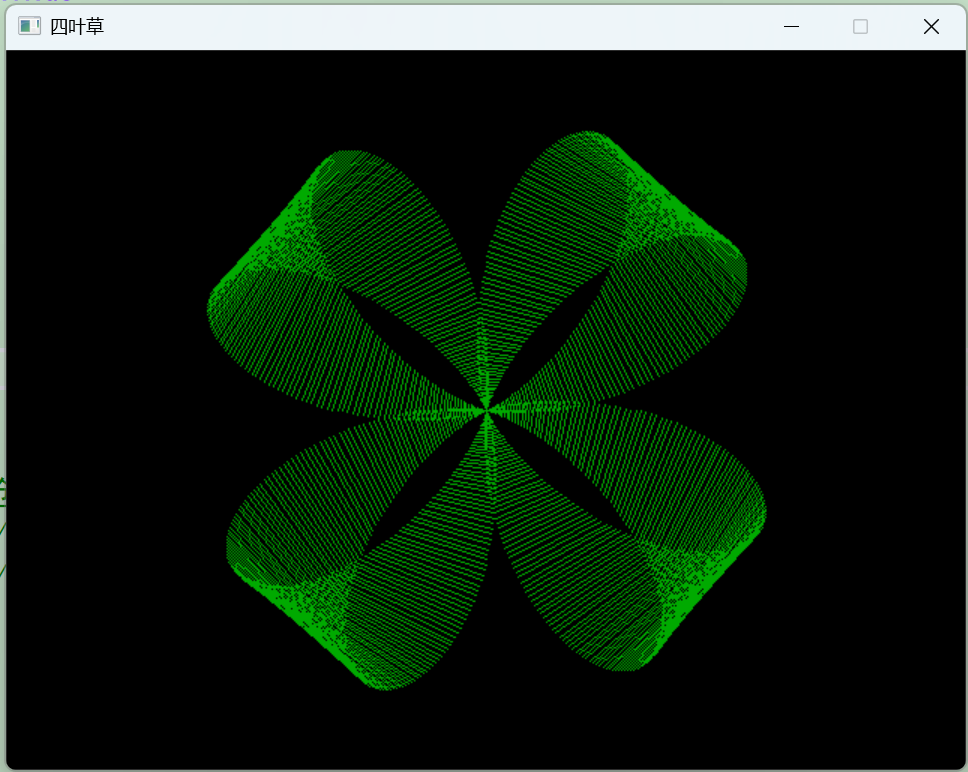
绘制四叶草的过程是一个动态的过程，因此博客中所展示的为绘制完成的四叶草。

2. 源码展示

复制代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>
#include<conio.h>
#include <graphics.h>

#define PI 3.1415926535

void main(void) 
{
	//初始化绘图窗口
	initgraph(640,480); //创建绘图窗口
	setcolor(GREEN);      //设置绘图颜色
	setorigin(320,240);  //设置原点坐标

	//画花朵
	double e;
	int x1, y1, x2, y2;
	for (double a = 0; a < 2 * PI; a += 2 * PI / 720)
	{
		e = 100 * (1 + sin(4 * a));
		x1 = (int)(e * cos(a));
		y1 = (int)(e * sin(a));
		x2 = (int)(e * cos(a + PI / 5));
		y2 = (int)(e * sin(a + PI / 5));

		line(x1, y1, x2, y2);

		Sleep(20);
	}

	_getch();
	closegraph();
}

3.逻辑概述

3.1 初始化图形环境

使用initgraph(640,480)创建了一个 640×480 像素的绘图窗口
设置绘图颜色为绿色 (GREEN)
将坐标系原点设置到窗口中心 (320, 240)

3.2 参数方程计算四叶草形状

使用极坐标方程 e = 100 * (1 + sin(4a)) 计算花瓣的轮廓
sin(4a) 中的系数 4 决定了花瓣数量（8 个花瓣）
当 a 从 0 到 2π 变化时，e 的值周期性变化形成花瓣形状

3.3 动态绘制四叶草

通过 720 次循环，每次增加微小角度增量 (2π/720)

对每个角度 a 计算两个点 ：

复制代码

x1 = e·cos(a), y1 = e·sin(a)
x2 = e·cos(a+π/5), y2 = e·sin(a+π/5)

连接这两个点形成线段，构成花朵的一部分
每次绘制后暂停 20 毫秒，形成动画效果

4. 参数改变

如果诸君对该程序想有所拓展，可以通过一些参数的修改改变四叶草的形状。

sin(4 * a) 中的系数 4 → 控制花瓣数量
PI / 5 → 控制线段连接角度
100 → 控制花朵大小
Sleep(20) → 控制绘制速度

5.小结

以上便是本篇博客的所有内容了，如果大家学到知识的话，还请给博主点点赞。