单因子实验方差分析模型的适应性检验

本文是实验设计与分析（第6版，Montgomery著傅珏生译)第3章单因子实验 方差分析第3.4节的python解决方案。本文尽量避免重复书中的理论，着于提供python解决方案，并与原书的运算结果进行对比。您可以从http://www.aluoyun.cn/details.php?article_id=36 下载实验设计与分析（第6版，Montgomery著傅珏生译)电子版。本文假定您已具备python基础，如果您还没有python的基础，可以从http://www.aluoyun.cn/details.php?article_id=26 下载相关资料进行学习。

残差检验是任一方差分析不可缺少的部分。如果模型是适合的，则残差是无定形的。也就是说，它们没有明显的模式。通过研究残差，可以发现很多模型不适合和基本假定不符合的例子。在这部分，我们将说明如何通过采用残差的图形分析来很容易地进行模型诊断检测，以及如何处置几种常见的反常现象。

3.4.1正态性假设

检验正态性假设可以利用残差直方图。如果满足关于误差的NID（O，s2）假定，则此直方图就应该类似于取自中心在零点处的正态分布的样本。可惜，对于小样本，经常会出现明显的波动，所以图像上中度偏离正态性的出现并不一定意味着严重违背正态性假定。而图像上对于正态性的严重偏离则有严重违背正态性假定的可能，并需要进行进一步的分析。

另一种极其有用的方法是构造一个残差的正态概率图。回顾第2章的飞检验，我们用原始数据画成的正态概率图来检验正态性假设。在方差分析中，对残差这样做通常更有效（且更直接）。如果潜在的误差分布是正态的，则图像呈直线状。在想象这一直线时，与极端值点相比，我们应该更看重直线附近的值点。

表3.6列出了例3.1中的蚀刻速率数据的原始数据和残差。图3.4是残差的正态概率图，审视这个图形，总的印象是误差分布是近似正态的。正态概率图在左边稍下弯曲，在右边稍有上磁，这意味着误差分布的尾部比起正态分布的尾部要更细一些：也就是说，最大的残差不完全如所期望的那样大（在绝对值的意义下）。但是，此图总体看起来却是正态的。

一般地，在固定效应方差分析中适度地偏离正态性我们并不大在意（回顾在3.3.2节中对随机化试验的讨论）。比起偏态分布来说，我们更为关心的是比正态分布的尾部明显的厚或薄的误差分布。因为F检验法只受轻微的影响，所以我们说，方差分析（及其有关的方法，例如多重比较法）对正态性假定是稳健的。偏离正态性通常会引起真正的显著性水平和功率与名义上的数值稍有差异，一般来说，功率会偏低。我们将在第12章中讨论的随机效应模型较多地受到非正态性的影响。

将以下数据保存为anovaoneway.txt

A B C D

575 565 600 725

542 593 651 700

530 590 610 715

539 579 637 685

570 610 629 710

#以下为3.1 图3.4pyhthon代码，与"anovaoneway.txt"放在同一目录下

import pandas as pd

import seaborn as sns

import statsmodels.api as sm

from statsmodels.formula.api import ols

load data file

d = pd.read_csv("anovatwoway.txt", sep="\t")

reshape the d dataframe suitable for statsmodels package

df_melt = pd.melt(df.reset_index(), id_vars=['index'], value_vars=['A', 'B', 'C', 'D'])

replace column names

df_melt.columns = ['index', 'treatments', 'value']

Ordinary Least Squares (OLS) model

model = ols('value ~ C(treatments)', data=df_melt).fit()

anova_table = sm.stats.anova_lm(model, typ=2)

anova_table

d['predicted']=model.predict()

d['residuals']=d.predicted-d.value

stats.normaltest(d.residuals)

>>> stats.normaltest(d.residuals)

NormaltestResult(statistic=3.718241068242035, pvalue=0.15580959935564462)

stats.probplot(d.residuals, plot=plt)

Plt.show()

import statsmodels.api as sm

import matplotlib.pyplot as plt

sm.qqplot(d.residuals,line='s')

#sm.qqplot(d.residuals)

plt.xlabel("Theoretical Quantiles")

plt.ylabel("Standardized Residuals")

plt.show()

fig, ax = plt.subplots(figsize=[5, 5])

sm.qqplot(d.residuals, line='s', ax=ax)

ax.get_lines()[0].set_color('grey')

ax.get_lines()[0].set_markerfacecolor('none')

ax.get_lines()[1].set_color('black')

plt.show()

# histogram

plt.hist(d.residuals,bins='auto',histtype='bar',ec='k')
plt.xlabel("Residuals")
plt.ylabel('Frequency')
plt.show()

res = stats.probplot(d.residuals)

r2_normal = res[1][2] ** 2

res = stats.probplot(d.residuals, dist=stats.lognorm, sparams=[1])

r2_lognormal = res[1][2] ** 2

plt.show()

正态概率图上的一种十分普遍的毛病，是有一个残差远大于其他的残差。这样的一个残差通常叫做异常值（outlier）。一个或多个异常值的出现会严重干扰方差分析，所以，要小心探究出现的异常值。引起异常值的原因经常是由于计算发生错误、规范数据或复制数据造成的误差所致。否则，则必须仔细研究该实验周围的实验环境。如果异常的响应是一个特别希望得到的值（高强度，低价格，等等），则异常值比其他数值更为有用。不要轻易拒绝或放弃一个异常的观测值，除非有合理的非统计性的根据。就是在最不利的情况下，也要做两次分析，一次包括异常值，另一次别除异常值。

有几种正式的统计方法可用来检测异常值[例如，参阅Barnett and Lewis（1994），Johnand Prescott（1975），以及Stefansky（1972）]。粗略检测异常值可以由验算标准化残差来做。

3.4.2依时间序列的残差图

依时间序列的残差图依照收集数据的时间顺序画出残差图有助于检测残差之间的相关性。具有正残差和负残差的趋势表明了正相关性。而这说明不符合误差的独立性假定（independence assumption）。这是一个潜在的严重问题且难于校正的问题，所以，要在收集数据时尽可能地防止这一问题的发生。而实验的适当随机化是获得独立性的一个重要步骤。

有时，实验者（或主体）的技巧可能会在实验进程中改变，或者，所研究的过程可能"漂移"或变得更加不稳定。这经常会导致误差方差随时间而改变。此条件常使残差关于时间的图形在一边比另一边更为伸展。非常数方差是一个潜在的严重问题.我们将在3.4.3节和3.4.4节中更多地讨论这个主题。

表3.6列出了例3，1中蚀刻速率数据的残差和收集数据的时间序列。残差与试验次序或时间的关系图如图35所示.没有理由去怀疑存在违反独立性或常数方差的假定。

3.4.3残差与拟合值的关系图

如果模型是正确的并且满足假定的条件，则残差应该是无定形的。特别地，它们应该与任一其他变量没有任何关系，自然也与用来预测响应的变量无关。一种简单的检测法是画出残差与拟合值的关系图。[对单因子实验模型来说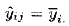，即第i种处理的平均值）。]该图应不显现出任何明显的模式.图3.6是例3.1中蚀刻速率数据的残差与拟合值的关系图。没有出现异常的结构。

从这种图形上偶尔会检测出非常数的方差。有时，观测值的方差会随着观测值数量的增加而增加。如果实验中的误差或背景噪音所占观测值大小的比例是一常数的话，这种情况就会发生。（这通常出现在测量工具的误差是读数尺寸的百分比的时侯。）万一出现这种情况，那么残差会随着yij的增大而增大，而残差与的关系图看起来就像一个向外开口的漏斗或喇叭简。当数据服从非正态的偏态分布时也会出现非常数方差，因为在偏态分布中，方差大体上是均值的函数。

如果违反了方差的齐性假定，则F检验法在平衡（所有处理的样本量相等）固定效应模型中只会受到轻微的影响。但是，在不平衡设计或一个方差远大于其他方差的情形中，问题就比较严重了。特别地，如果因子水平有很大的方差，同时有较小的样本量，则实际的第一类错误率远大于期望值（或置信水平比预期的低）。相反，如果因子水平有很大的方差，同时有较大的样本量，则显著水平比预期的要小（置信水平比预期的高）。这是尽可能选择等样本量（equal sample sizs）的一个充分理由。对于随机效应模型，不相等的误差方差可能会显著地干扰关于方差分量的推断，即使用平衡设计也是如此。

当非常数方差是因为上面的理由而出现的时候，通常的处理方案是应用方差稳定化变换（variance-stabilizing transformation），然后对变换后的数据进行方差分析。注意在这种处理方案中，我们是对经过变换后的总体应用方差分析的结论。

关于如何选取恰当的变换己有相当多的研究。如果实验者知道观测值的理论分布，他们就可以利用这一信息来选取变换。例如，如果观测值服从泊松分布，则可以用平方根变换。如果数据服从对数正态分布，则可用对数变换。对用分数表示的二项分布数据，则用反正弦变换。在没有明显的变换时，实验者通常凭经验来寻找使方差不变的变换，而不管均值的数值如何。在第5章所讨论的析因实验中，另一种处理方案是选取使交互作用的均方取最小值的变换，使实验所得的结果较易于解释。在第15章中，我们将较详细地讨论选取变换的解析方法。对方差的不等性所作的变换也会影响到误差分布的形式。在大多数情况下，变换带来的误差分布更接近于正态分布，关于变换的更详细的讨论，请参Bartlett（1947），Box and Cox（1964），Dolby（1963），Draper and Hunter（1969）。

1.方差相等性的统计检验

     一个广为应用的方法是Bartlet比检验法.

Bartlett检验法对正态性假定非常敏感，当怀疑正态性假定时，最好不要使用Bartlett检验法。

例3.4因为正态性假定不成问题，我们将Bartlett检验法应用于例3.1中的蚀刻速率实验数据。首先计算每种处理的样本方差，求得S12=400.7，S22=280.3，S32=421.3，S42=232.5。则

检验统计量是

因为，所以不能拒绝零假设，且结论是，所有4个方差是相同的。分析残差与拟合值的关系图也能得到同样的结论。

import scipy.stats as stat

sw,pvalue=stats.shapiro(d.residuals)

print(sw,pvalue)

print(sw, pvalue)

As the p value is non significant, we fail to reject null hypothesis and conclude that data is drawn from normal distribution.

import pandas as pd

df = pd.read_csv("anovaoneway.txt", sep="\t")

import scipy.stats as stat

sw,pvalue=stats.bartlett(df['A'],df['B'],df['C'],df['D'])

print(sw,pvalue)

print(sw, pvalue)

As the p value is non significant, we fail to reject null hypothesis and conclude that treatments have equal variances.

因为Bartlett检验法对正态性假定非常敏感，所以提出另一种方法也许是合适的。Ander-son and McLean（1974）很好地讨论了关于方差相等性的统计检验。修正后的Levene检验[见Levene（1960）和Conover，Johoson，and Johoson（1981）]是一种非常好的方法，它对正态性的偏离是稳健的。修正后的Levene检验评估了所有处理的平均偏差是相等的还是不等的。如果这些平均偏差是相等的，则所有处理中的观测值的方差将是相同的。Levene检验的检验统计量只是简单地把通常用于检验均值相等的ANOVA F统计量用到了绝对偏差上。

例3.5一位土木工程师试图确定：4种不同的洪水流量频率的估计方法在应用于同一流域时，是否能产生相同的峰值排水量估计。每种方法在此流域中使用6次，所得的排水量数据（单位为每秒立方英尺）如表3.7的上半部所示。数据的方差分析概括在表3.8中，它表明4种方法给出的洪峰排水量的均值不同。残差与拟合值的关系图如图3.7所示，令人不爽的是，开口向外的漏斗型表明所得数据不满足常值方差的假定

我们用修正后的Levene方法检验峰值排水量数据。表3.7的左半部含有处理的中位数：，而右半部含有对中位数的偏离dij。Levene检验进行dij的方差标准分析。得到的F检验统计量Fo=4.55，其P值是P=0.0137。因此，Levene检验拒绝了方差相等的零假设。我们的结论与图3.7所显示的信息一致。

峰值排水量数据是数据变换的一个好的例子。

将以下数据保存为anovaoneway.txt

A B C D

0.34 0.91 6.31 17.15

0.12 2.94 8.37 11.82

1.23 2.14 9.75 10.95

0.70 2.36 6.09 17.20

1.75 2.86 9.82 14.35

0.12 4.55 7.24 16.82

Levene's test can be used to check the Homogeneity of variances when the data is not drawn from normal distribution.

import pandas as pd

import scipy.stats as stats

df = pd.read_csv("anovaoneway.txt", sep="\t")

res=stats.levene(df['A'], df['B'], df['C'], df['D'])

statistic,pvalue=res

print ('statistic: ',statistic)

print ('pvalue: ',pvalue)

2.变换的经验选择（略，见原书）

3.4.4残差与其他变量的关系图

如果数据收集时还跟其他可能影响响应的变量有关，则应画出残差与那些变量的关系图。例如，在例3.1的蚀刻速率实验中，蚀刻速率可能受气压的显著影响，所以，应该画出残差与气压的关系图。如果用不同的蚀刻机来收集数据，则应画出残差与那些机器的关系图。只要在这类残差中呈现一定的棋式，就意味着相应变量影响响应。对于这种变量或者在将来的实验中更谨慎地控制，或者将它也包括在数据分析中。