GESPC++六级复习

1.树

1.树的基本概念

1.1.讲解

（0基础先大概浏览加粗部分）。

1.树：由若干个节点以及若干条边组成的具有层级关系且非线性的数据结构。
2.根节点：（Root）树的最顶层节点。
3.父节点：（Parent Node）节点沿着边往上一层的结点称为该节点的父节点。
4.子节点：（Child Node） 节点沿着边往下一层的结点称为该节点的子节点。
5.兄弟节点：（Sibling）同一个父亲节点的子节点互为兄弟节点。
6.叶子结点：（Leaf）没有子节点的节点称为叶子结点。
7.子树：（Subtree）以某个子节点为根节点的树分支。
8.节点的深度：（Depth）是指从根节点到该节点的距离。
9.节点的高度：（Height）该节点到叶子结点的最长距离。
10.树的高度：（Height of tree）根节点到叶子结点的最长距离。
11.节点的层级：（Level）该节点的父节点数量+1。
12.节点的度：（Degree）该节点的子节点数量。

你可能不懂，不妨看下面例子：

在上图中，是一棵树（见上1.树）。

其中根节点是1（根节点就是树冠，见上2.根节点）。

我们称1是2和3的父节点（见上3.父节点），反之，2和3是1的子节点（见上4.子节点）。

看到12和13，我们称它们互为兄弟节点（见上5.兄弟节点）。

再看到最后一层（这只是一个例子，不一定所有叶子结点都在最后一层哟！），我们称8至15都是这棵树的叶子结点（见上6.叶子结点）。

子树：仍然以上图为例，下图是上图中的一个子树（见上7.子树）。

相信上面的知识你懂了，但是下面的认真看，有点点难哟！

在图中，根节点 1 的深度为 0；节点 2 和 3 的深度为 1，因为从根节点 1 到节点 2 或 3 只经过 1 条边；节点 4、5、6、7 的深度为 2。（见上8.节点的深度）

接下来这个东西千万千万千万不要跟下面的搞混了！！！

叶子节点 8、9、10、11、12、13、14、15 的高度为 0，因为它们本身就是叶子节点；节点 4 的高度为 1，因为从节点 4 到叶子节点 8 或 9 最长距离是 1 条边。（见上9.节点的高度）

如果说8.9.是一组，那么10.11也是一组。

根节点到叶子节点的最长距离就是树的高度。图中从根节点 1 到最底层的叶子节点 8、9、10、11、12、13、14、15，最长距离是 3 条边，所以这棵树的高度为 3。（见上10.树的高度）

节点的父节点数量加 1 就是该节点的层级。根节点 1 没有父节点，它的父节点数量是 0，所以层级是 1；节点 2 和 3 有 1 个父节点（即根节点 1），它们的层级是 2（见上11.节点的层级）

节点的子节点数量就是节点的度。根节点 1 的度为 2，因为它有节点 2 和 3 两个子节点；节点 2 的度为 2，有节点 4 和 5 两个子节点；节点 3 的度为 2 ，有节点 6 和 7 两个子节点（节点的度）

1.2.题目练习

节点深度相关

已知一棵二叉树，根节点 A 下有子节点 B 和 C，B 节点下有子节点 D 和 E，节点 E 的深度是（ ）。

节点高度相关

在一棵树中，节点 F 有两个子节点 G 和 H，G 节点没有子节点，H 节点下有子节点 I 和 J，节点 F 的高度是（ ）。

树的高度相关

一棵树包含根节点 K，其下有三个子节点 L、M、N。L 节点下有四层子节点，M 节点下有两层子节点，N 节点下有三层子节点，这棵树的高度是（ ）

节点层级相关

有一棵树，根节点为 O，根节点下有两个子节点 P 和 Q，P 节点下又有三个子节点 R、S、T，节点 S 的层级是（ ）。

节点的度相关

在一棵树中，节点 U 有三个子节点 V、W、X，节点 V 有一个子节点 Y，节点 W 没有子节点，节点 X 有四个子节点，节点 U 的度是（ ），节点 V 的度是（ ）。

答案：

1. 2

2. 2

3. 5

4. 3

5. 3，1

2.二叉树的基本概念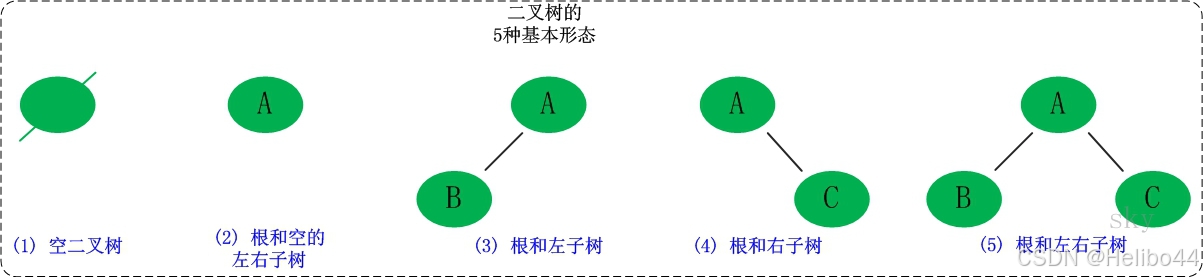

二叉树的概念很简单，二叉树，就是除了叶子结点的所有节点度都为2，叶子结点度为0（没有儿子节点）。

3.树和二叉树的基本性质

性质：

证明：

树：

二叉树：

4.特殊树：

完全二叉树（complete binary tree）：除了最后一层，其他所有层次都被填满的二叉树。

满二叉树（full binary tree）：除了叶子节点以外，其他结点的度均为2的二叉树(特殊完全二叉树)。

完美二叉树（perfect binary tree）：所有叶子结点均在同一层，其他节点的度均为2的二叉树。

二叉搜索树（binary search tree）：

1.若它的左子树不为空，则左子树上所有节点的值都小于根节点的值。

2.若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。

3.它的左右子树也分别为二叉搜索树。

4.中序遍历有序。

5.如果为空，无视1234性质。

平衡二叉树：

1.左右子树的高度之差的绝对值不能超过1。

2.任何一个节点的左右子树都是平衡二叉树。

二叉排序树：

1.左子树节点值<根节点值<右子树根节点值。

2.左子树和右子树又各是一棵二叉排序树。

3.如果为空，无视12性质。

注：二叉搜索树和二叉排序树是一个概念

路径：某节点到另一节点所经过的所有节点。

路径长度：从某节点到另一节点所经过边的数量。

节点的带权路径长度：这个值=树的根节点到该节点的路径长度*该节点的权重。

树的带权路径长度：这个值=所有叶子结点的带权路径长度之和，简称WPL。

哈夫曼树：在叶子节点和权重确定的情况下，带权路径长度最小的二叉也被称为最优二叉树。

构建哈夫曼树的方法：

1：把每一个节点都当成一颗独立的树。这样就形成了一个森林。

2：选择当前权重最小的两个节点，生成新的父节点。

3：从队列中移除上一步选择的两个最小节点，把新的父节点加入队列。

4：重复第23步。一直到队列为空，也就是没有节点的时候结束。

5.遍历方式：

深搜：

前序遍历：根左右。

中序遍历：左根右。

后序遍历：左右根。

广搜：

层次遍历：按层次遍历即可。

例如，求下边二叉树的各种遍历。

答案：

前序遍历：1 2 4 5 3 6 7

中序遍历：4 2 5 1 6 3 7

后序遍历：4 5 2 6 7 3 1

层次遍历：1 2 3 4 5 6 7

代码：

#include <bits/stdc++.h>
#include <vector>
#include <queue>
using namespace std;

// 定义二叉树节点结构
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 构建二叉树
TreeNode* buildTree() {
    string val;
    cin >> val;
    if (val == "#") {
        return NULL;
    }
    TreeNode* root = new TreeNode(stoi(val));
    queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* node = q.front();
        q.pop();
        cin >> val;
        if (val != "#") {
            node->left = new TreeNode(stoi(val));
            q.push(node->left);
        }
        cin >> val;
        if (val != "#") {
            node->right = new TreeNode(stoi(val));
            q.push(node->right);
        }
    }
    return root;
}

// 前序遍历（深搜）
void preorderTraversal(TreeNode* root, vector<int>& result) {
    if (root == NULL) {
        return;
    }
    result.push_back(root->val);
    preorderTraversal(root->left, result);
    preorderTraversal(root->right, result);
}

// 中序遍历（深搜）
void inorderTraversal(TreeNode* root, vector<int>& result) {
    if (root == NULL) {
        return;
    }
    inorderTraversal(root->left, result);
    result.push_back(root->val);
    inorderTraversal(root->right, result);
}

// 后序遍历（深搜）
void postorderTraversal(TreeNode* root, vector<int>& result) {
    if (root == NULL) {
        return;
    }
    postorderTraversal(root->left, result);
    postorderTraversal(root->right, result);
    result.push_back(root->val);
}

// 层次遍历（广搜）
void levelOrderTraversal(TreeNode* root, vector<int>& result) {
    if (root == NULL) {
        return;
    }
    queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* node = q.front();
        q.pop();
        result.push_back(node->val);
        if (node->left) {
            q.push(node->left);
        }
        if (node->right) {
            q.push(node->right);
        }
    }
}

// 辅助函数，用于打印结果
void printVector(const vector<int>& vec) {
    for (int num : vec) {
        cout << num << " ";
    }
    cout << endl;
}

int main() {
    cout << "请按层输入二叉树节点值，空节点用 # 表示：" << endl;
    TreeNode* root = buildTree();

    vector<int> preorderResult;
    preorderTraversal(root, preorderResult);
    cout << "前序遍历结果: ";
    printVector(preorderResult);

    vector<int> inorderResult;
    inorderTraversal(root, inorderResult);
    cout << "中序遍历结果: ";
    printVector(inorderResult);

    vector<int> postorderResult;
    postorderTraversal(root, postorderResult);
    cout << "后序遍历结果: ";
    printVector(postorderResult);

    vector<int> levelOrderResult;
    levelOrderTraversal(root, levelOrderResult);
    cout << "层次遍历结果: ";
    printVector(levelOrderResult);

    return 0;
}

2.编码

一、哈夫曼编码​

（一）编码基础概念​

在开始学习哈夫曼编码前，我们得先理解一些基本概念。我们日常使用的文本，比如一篇文章，本质上在计算机里都是由一个个字符组成。每个字符在计算机中都有对应的二进制编码，常见的 ASCII 编码就是一种方式，比如字母 'a' 对应二进制的 01100001 。但这种固定长度的编码方式，在一些情况下会造成存储空间的浪费。假如我们有一段文本，里面大部分字符都是 'a' ，少部分是其他字符，要是都用固定长度编码，对于大量重复的 'a' 就不划算，这时候就需要更高效的编码方式，哈夫曼编码就应运而生。​

（二）哈夫曼编码原理​

哈夫曼编码是一种数据压缩算法，它的核心思路是根据字符在数据中出现的频率来构建一棵特殊的树 ------ 哈夫曼树。频率高的字符在树中处于靠近顶部的浅层位置，它的编码就短；频率低的字符在树的深层位置，编码就长。通过这种变长编码，整体上能减少数据存储占用的空间。举个例子，假设有一篇文章，字母 'e' 出现的次数最多，那么在哈夫曼编码里，'e' 可能就会被赋予一个很短的编码，比如 '0' ，这样在存储这篇文章时，用 '0' 代替所有的 'e' ，就能节省空间。​

（三）哈夫曼编码实现步骤

1.统计字符频率

这一步就是数一数每个字符在要编码的数据里出现了多少次。比如有个字符串 "ababccc" ，我们就统计出 'a' 出现 2 次，'b' 出现 2 次，'c' 出现 3 次。

2.构建哈夫曼树：

• 给每个字符创建一个节点，节点里记录这个字符以及它出现的频率。像上面例子里，就创建分别代表 'a' 'b' 'c' 的节点，每个节点记录对应频率。

• 把这些节点都放进一个优先队列（简单理解就是一个会自动按特定规则排序的容器），这里按频率从小到大排序。

• 不断从队列里拿出两个频率最小的节点，创建一个新的父节点。新父节点的频率是这两个子节点频率之和。比如先拿出代表 'a' 和 'b' 的节点（假设它们频率最小），创建一个新节点，频率是 2 + 2 = 4 。

• 把新的父节点放回队列，一直重复这个过程，直到队列里只剩下一个节点，这个节点就是哈夫曼树的根节点。

3.生成哈夫曼编码

从根节点开始，沿着树的分支走。向左走就记为 '0' ，向右走记为 '1' 。当走到叶子节点（也就是代表具体字符的节点）时，记录下从根节点到这个叶子节点走过的路径，这就是该字符的哈夫曼编码。比如从根节点出发，向左走两步到了代表 'a' 的节点，那么 'a' 的编码就是 '00' 。

4.编码数据

根据前面生成的哈夫曼编码表，把要编码的数据里每个字符都替换成对应的编码。比如数据是 "ab" ，如果 'a' 编码是 '00' ，'b' 编码是 '01' ，那么编码后的数据就是 '0001' 。​

5.解码数据

解码时，从编码数据的开头开始，按位对照哈夫曼树的路径走。比如编码数据是 '0001' ，从根节点开始，遇到 '0' 向左走，再遇到 '0' 又向左走，走到代表 'a' 的节点，就解码出一个 'a' ，接着对后面的 '01' 重复这个过程，直到解码完所有数据。

例题（选自数据结构练习题【哈夫曼树、图、排序、散列表】_哈夫曼树练习题-CSDN博客）

假设用于通讯的电文由8种字母组成，字母及其在电文中出现的频率如下所示:

字母	A	B	C	D	E	F	G
频率	0.07	0.12	0.20	0.32	0.16	0.03	0.10

有⼀电⽂共使⽤五种字符 a, b, c, d, e，其出现频率依次为 4, 7, 5, 2, 9

试画出对应的编码哈夫曼树（要求左⼦树根结点的权⼩于等于右⼦树根结点的权）

计算该树的带权路径长度

求出每个字符的哈夫曼编码

求出传送电⽂的总长度

并译出编码系列11 00 011 10 00 10 10 11的相应电⽂。

二、格雷编码

（一）格雷编码概念引入​

格雷编码也是一种二进制编码方式。在一些数字系统中，比如数据传输或者计数器场景下，普通二进制编码在状态切换时，可能会有多位同时变化的情况。这就容易产生错误，因为电路等硬件在处理多位同时变化时可能会有延迟等问题。格雷编码的特点就是相邻的两个编码只有一位不同，很好地解决了这个问题。​

（二）格雷编码原理​

格雷编码可以通过对普通二进制编码进行转换得到。它的设计思路就是保证相邻的数值对应的编码只有一位差异，这样在系统状态切换时，出错的概率就大大降低。

（三）格雷编码实现步骤

二进制转格雷码

对于一个 n 位的二进制数 B ，它对应的格雷码 G 的第 i 位（从右往左数，i 从 0 开始），计算公式是：G [i] = B [i] ^ B [i + 1] 。这里的 '^' 是异或运算，意思是两个数不同时结果为 1 ，相同时结果为 0 ，并且 B [n] 规定为 0 。比如二进制数 1010 ，计算它的格雷码。从右往左，第 0 位：B [0] ^ B [1] = 0 ^ 1 = 1 ；第 1 位：B [1] ^ B [2] = 1 ^ 0 = 1 ；第 2 位：B [2] ^ B [3] = 0 ^ 1 = 1 ；第 3 位：B [3] ^ B [4]（B [4] 按规定为 0 ） = 1 ^ 0 = 1 ，所以 1010 对应的格雷码就是 1111 。

格雷码转二进制

已知格雷码 G 求二进制数 B ，B [0] = G [0] ，然后从第 1 位到第 n - 1 位，B [i] = B [i - 1] ^ G [i] 。比如格雷码 1111 ，B [0] = G [0] = 1 ，B [1] = B [0] ^ G [1] = 1 ^ 1 = 0 ，B [2] = B [1] ^ G [2] = 0 ^ 1 = 1 ，B [3] = B [2] ^ G [3] = 1 ^ 1 = 0 ，所以对应的二进制数就是 1010 。

例题

以下关于格雷码的描述哪些是正确的？

A. 卡诺图的坐标是按照格雷码的顺序标注的

B. 格雷码0110对应的二进制数是0100

C. 格雷码相邻的码组间仅有一位不同

D. 格雷码从编码形式上杜绝了逻辑冒险的发生

E. 格雷码常用于提高单一时钟域内总线数据的可靠信

答案：ABCD

解析：竞争冒险主要由于组合逻辑的两个输入同时向不同的方向变化，并且变化不同步导致的，而格雷码使得组合逻辑的输入端只有一个发生变化，因此杜绝了逻辑冒险的发生。

本文章总结了所有面向对象可能会用到的笔记以及知识，同时也是c++GESP6级的必考题，不推荐0基础阅读，请见谅！

3.面向对象

一.面向对象三大特性

C++面向对象的三大特性：封装、继承、多态

1.封装

1.1封装的意义

封装的意义如下：

• 将属性/行为作为整体，表现人、事、物。
• 将属性/行为加以权限以便控制。

1.2封装的格式（语法）：

class 类名{
    访问权限： 属性 / 行为
};

解释如下：

类名就是类的名字，访问权限一般有三种：

1. public 公共权限
2. protected 保护权限
3. private 私有权限

这三条也就是封装的第二条意义：将属性/行为加以权限以便控制。

2.继承

2.1继承的意义

继承的意义如下：利用继承的技术，减少重复代码。

2.2继承的好处

继承的好处：可以减少重复的代码

2.3继承的语法（格式）

语法（格式）：

class 子类 : 继承方式 父类

A 类称为子类 或 派生类；

B 类称为父类 或 基类。

2.4派生类成员分类

派生类中的成员，包含两大部分：

1.从基类继承过来的，2.自己增加的成员。

从基类继承过过来的表现其共性，而新增的成员体现了其个性。

2.5继承方式汇总

相信大家在看语法的时候愣在了继承方式，其实非常easy。

三大继承方式：

• 公共继承
• 保护继承
• 私有继承

3.多态

3.1多态的意义

3.1.1分类

多态分为两类

• 静态多态: 函数重载 和 运算符重载属于静态多态，复用函数名
• 动态多态: 派生类和虚函数实现运行时多态

3.1.2区别

静态多态和动态多态区别：

• 静态多态的函数地址早绑定 - 编译阶段确定函数地址
• 动态多态的函数地址晚绑定 - 运行阶段确定函数地址

3.2总结

多态满足条件

• 有继承关系
• 子类重写父类中的虚函数

多态使用条件

• 父类指针或引用指向子类对象

重写：函数返回值类型、函数名、参数列表完全一致称为重写

二.运算符重载

运算符重载概念：对已有的运算符重新进行定义，赋予其另一种功能，以适应不同的数据类型。

三.class与struct

在C++中 struct和class唯一的区别在于默认访问权限不同，如下：

• struct 默认权限为公共
• class 默认权限为私有