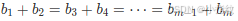目录
A-完美序列
解题思路
所谓完美序列,就是让我们找给定的序列a中,选任意元素任意排列顺序,能组成最长的一个满足
的序列的长度。那么我们可以用哈希表mp记录每个数字的个数,然后遍历可能的和的值2~10000,第二层循环从1 ~i/2,为了缩短时间同时防止重复记录,然后再令y=i-j,看满足这个条件的数有多少个,如果他的值和j相等,组合对数就加mp[j]/2,否则就取二者个数的最小值,最后更新一下最大值ans。输出即可。
AC代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=2e5+5;
const int inf=5000;
int n,num,mp[inf+10];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>num,mp[num]++;
int ans=0;
for(int i=2;i<=10000;i++)
{
int res=0;
for(int j=1;j<=i/2;j++)
{
int x=i-j;
if(x>inf)continue;
if(x==j)
res+=mp[x]/2;
else
res+=min(mp[x],mp[j]);
}
ans=max(res,ans);
}
cout<<ans*2;
}
signed main()
{
IOS;
int _=1;
// cin>>_;
while(_--)
solve();
return 0;
}C-合并石子
解题思路
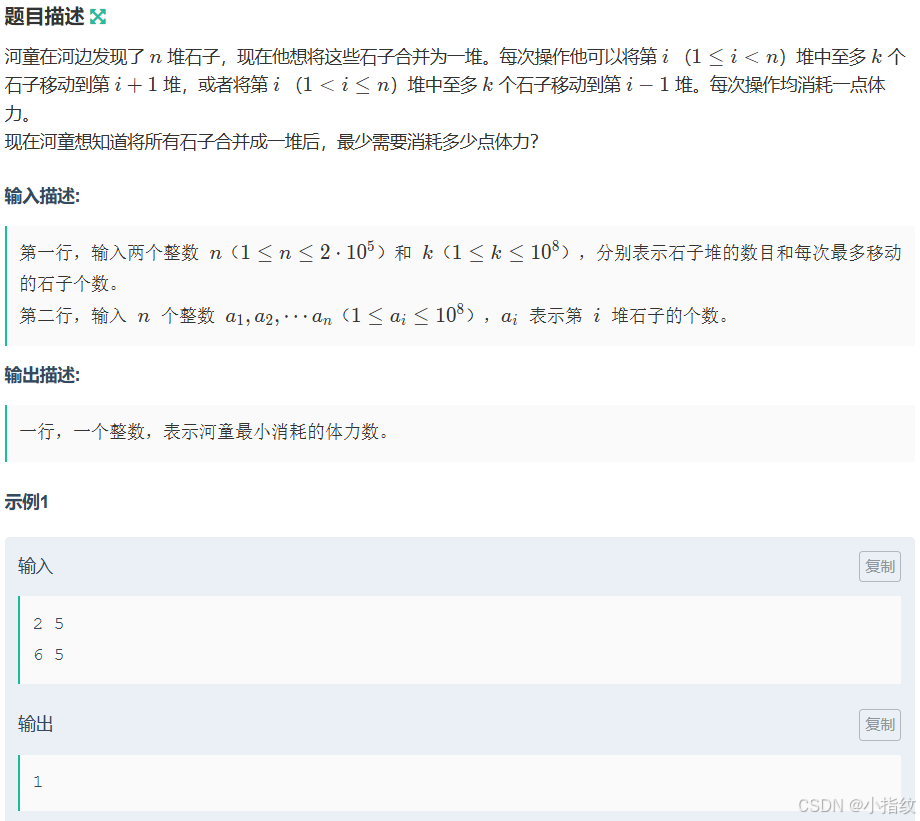
这道题我是分别记录位置i的左边所有数到达它需要的步数和右边所有数需要到达他的总步数,最后再将二者相加就是所有石子需要到达他的总步数。通过前缀和记录每个位置需要移动的石子个数,(数字+k-1)/k是向上取整的意思,再将每个位置的步数累加。然后遍历筛选一个最小的总和,ans初始值不能赋INT_MAX,不然会wa一半。。。因为题目中数字较大,所以初值赋1e18.
AC代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
int n,k,a[N],b[N],c[N],s1[N],s2[N],l[N],r[N];
void solve()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
l[i]=l[i-1]+a[i];
for(int i=n;i>=1;i--)
r[i]=r[i+1]+a[i];
for(int i=1;i<=n;i++)
s1[i]=s1[i-1]+(l[i]+k-1)/k;
for(int j=n;j>=1;j--)
s2[j]=s2[j+1]+(r[j]+k-1)/k;
int ans=1e18;
for(int i=1;i<=n;i++)
ans=min(ans,s1[i-1]+s2[i+1]);
cout<<ans;
}
signed main()
{
IOS;
int _=1;
// cin>>_;
while(_--)
solve();
return 0;
}G-封闭运算
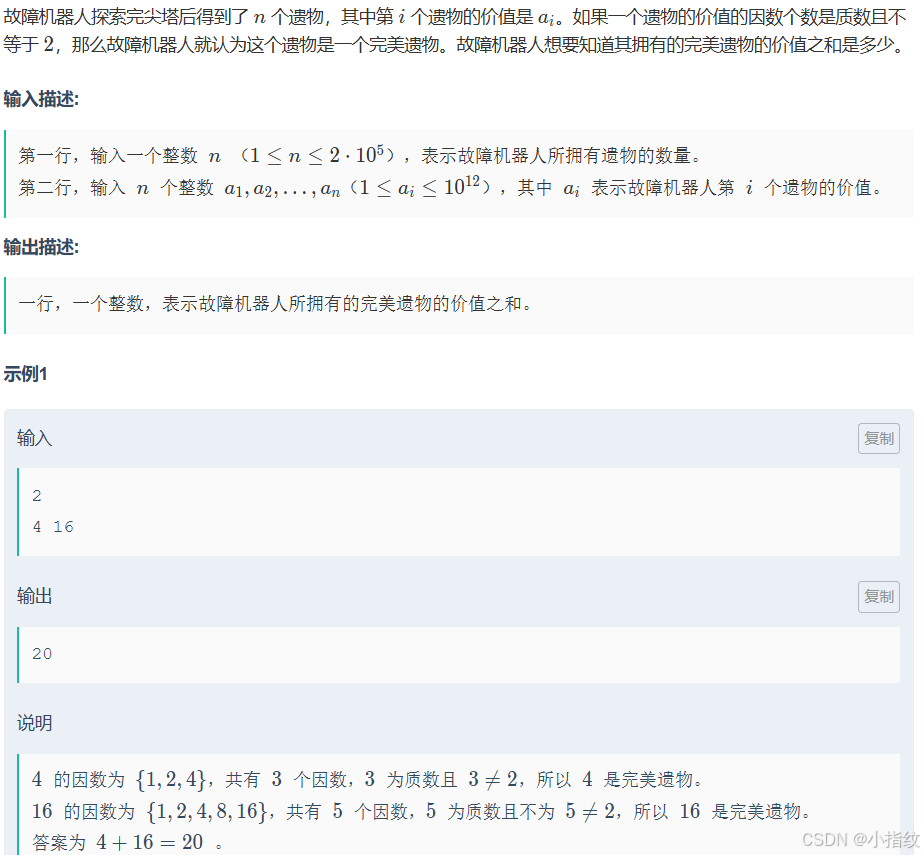
解题思路
将原有的值都标记,数据范围很小,开双层循环遍历,如果二者异或值在原数组中不存在就输出"NO"如果全都存在就输出"YES".
AC代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=106;
int n,a[N];
map<int,int>mp;
void solve()
{
cin>>n;
int f=1;
for(int i=1;i<=n;i++)
cin>>a[i],mp[a[i]]++;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
int x=a[i]|a[j];
if(mp[x]==0)
{
f=0;
break;
}
}
if(!f)
break;
}
if(f)
cout<<"YES";
else
cout<<"NO";
}
signed main()
{
IOS;
int _=1;
// cin>>_;
while(_--)
solve();
return 0;
}J-故障机器人的完美牌组
解题思路
简单的规律题,不过我错了很多发,第一看错题了,第二考虑少了。
首先如果是1,特判直接输出。
否则就从2~n找到最大值mx和最大值所在的位置j,然后看这个最大值是不是等于0,如果是,就不做处理,因为处理了不仅没有数变大而且长度会变小字典序就变小了。如果不是0,就将j标记,a[1]=a[1]+a[j],输出n-1,然后输出剩下的数,便利到j时不输出,因为已经用掉了。
AC代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6;
int n,a[N],mx=-1e10,j;
unordered_map<int,int>b;
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i],b[a[i]]++;
if(n==1)
{
cout<<n<<endl;
cout<<a[1]<<endl;
return ;
}
for(int i=2;i<=n;i++)
{
if(a[i]>=mx)
{
mx=a[i];
j=i;
}
}
if(mx!=0)
{
cout<<n-1<<endl;
cout<<a[1]+mx<<" ";
for(int i=2;i<=n;i++)
{
if(i!=j)
cout<<a[i]<<" ";
}
}
else
{
cout<<n<<endl;
for(int i=1;i<=n;i++)
cout<<a[i]<<" ";
}
}
signed main()
{
IOS;
int _=1;
// cin>>_;
while(_--)
solve();
return 0;
}L-故障机器人的完美遗物
解题思路
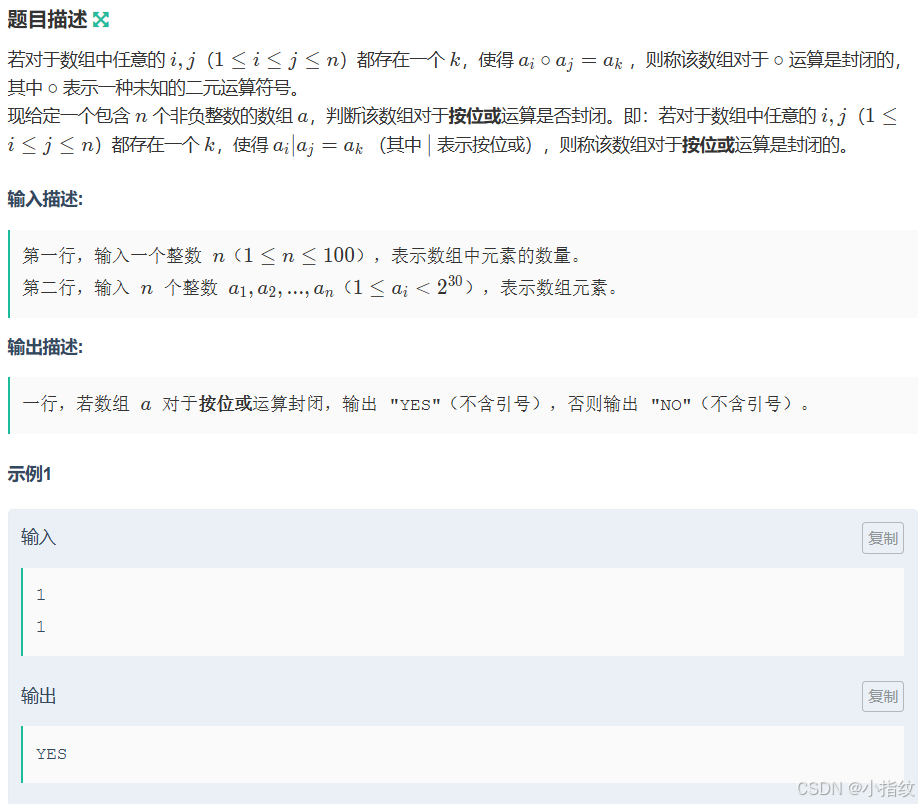
这道题的核心是判断一个数是否为"完美遗物",并计算所有完美遗物的价值之和 。完美遗物的定义是:该数的因数个数是质数且不等于 2。首先筛出可以开平方的数,这样它的因数一定是奇数个,就有可能是质数。
1. 数学原理(题解核心)

要让 ( d(n) ) 是质数且 ≠ 2,需满足:
- 因数个数的乘积结果是质数 → 乘积中只能有一个因子(否则质数相乘会得到合数)。
- 因此,( n ) 的素因数分解形式必须是 ( n = a^{b-1} ) (其中 ( a ) 是素数,( b ) 是质数且 ( b \neq 2 ) )。此时:
d(n) = (b-1 + 1) = b
( b ) 是质数且 ≠ 2,满足"完美遗物"条件。
2. 实现思路
(1)预处理素数(prime 函数)
用埃氏筛预处理出一定范围(如 ( 10^6 ) )内的素数,后续用于快速分解因数。
(2)因数个数计算(con 函数)
对输入的数 ( x ),先判断是否为平方数(因为完美遗物的形式是 ( a^{b-1} ),等价于平方数的变形)。若为平方数,对其平方根 ( \text{sqrt}(x) ) 做素因数分解,计算因数个数:
- 分解平方根的素因数,得到各素因子的指数 ( d )。
- 因数个数公式变为
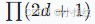
(因为原数是平方根的平方,指数翻倍)。
(3)筛选完美遗物(solve 函数)
遍历所有遗物值:
- 先判断是否为平方数(否则不可能满足 ( n = a^{b-1} ) 形式)。
- 对平方根分解,计算因数个数 ( f )。
- 检查 ( f ) 是否是质数且 ≠ 2,若是则累加价值。
(1)埃氏筛预处理素数
cpp
const int N = 1e6 + 5000;
int a[N], b[N], q, k = 0;
void prime() {
a[1] = 1; // 1 不是素数
for (int i = 2; i < N; i++) {
if (a[i] == 0) b[++k] = i; // 记录素数
for (int j = 1; j <= k && i * b[j] < N; j++) {
a[i * b[j]] = 1; // 标记非素数
if (i % b[j] == 0) break; // 保证每个合数只被最小素因子筛掉
}
}
}a[]标记是否为素数,b[]存储素数列表。- 埃氏筛的核心是"用已知素数标记其倍数",保证效率。
(2)因数个数计算(con 函数)
cpp
int con(int x) {
if (x == 1) return 1;
int c = 1;
for (int i = 1; i <= k; i++) {
int p = b[i];
if (p * p > x) break; // 超过平方根,无需继续
if (x % p == 0) {
int d = 0;
while (x % p == 0) { // 分解出所有 p 的因子
x /= p;
d++;
}
c *= (d * 2 + 1); // 原数是平方数,指数翻倍后计算因数个数
}
}
if (x > 1) c *= 3; // 剩余大素数因子(指数为1,翻倍后指数为2,d=1 → 2*1+1=3)
return c;
}(3)主函数(solve 函数)
cpp
void solve() {
int n, sum = 0;
prime(); // 预处理素数
cin >> n;
vector<int> e(n + 1);
for (int i = 1; i <= n; i++) cin >> e[i];
for (int i = 1; i <= n; i++) {
int x = e[i];
int ii = sqrt(x);
if (ii * ii != x) continue; // 不是平方数,直接跳过
int f = con(ii); // 计算平方根的因数个数(即原数的因数个数)
if (a[f] == 0 && f > 2) { // 因数个数是素数且 ≠2
sum += x;
}
}
cout << sum << endl;
}- 先筛出平方数(非平方数不可能满足完美遗物条件)。
- 对平方数,通过
con计算因数个数,再判断是否为"质数且 ≠2",若是则累加价值。
AC代码
cpp
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5000;
int a[N], b[N], k = 0; // a数组标记是否为素数,b数组存储素数
// 埃氏筛法预处理素数
void prime() {
a[1] = 1; // 1不是素数
for (int i = 2; i < N; i++) {
if (a[i] == 0) {
b[++k] = i; // 记录素数
}
// 标记非素数
for (int j = 1; j <= k && i * b[j] < N; j++) {
a[i * b[j]] = 1;
if (i % b[j] == 0) break; // 优化,避免重复标记
}
}
}
// 计算x的因数个数相关值(针对平方数的平方根)
int con(int x) {
if (x == 1) return 1;
int c = 1;
for (int i = 1; i <= k; i++) {
int p = b[i];
if (p * p > x) break; // 超过平方根,无需继续
if (x % p == 0) {
int d = 0;
// 分解出所有p的因子
while (x % p == 0) {
x /= p;
d++;
}
c *= (d * 2 + 1); // 计算因数个数
}
}
if (x > 1) c *= 3; // 处理剩余的大素数因子
return c;
}
signed main() {
prime(); // 预处理素数
int n, sum = 0;
cin >> n;
vector<int> e(n + 1);
for (int i = 1; i <= n; i++) {
cin >> e[i];
}
for (int i = 1; i <= n; i++) {
int x = e[i];
int ii = sqrt(x);
// 先判断是否为平方数(非平方数不可能是完美遗物)
if (ii * ii != x) continue;
// 计算因数个数
int f = con(ii);
// 判断因数个数是否为素数且不等于2
if (a[f] == 0 && f > 2) {
sum += x;
}
}
cout << sum << endl;
return 0;
}