数据预处理之数据平滑处理详解

信号数据收到噪声干扰，影响检测的准确性。数据平滑处理的关键步骤，旨在降低噪声同时保留信号特征。

1.1****移动平均（ Moving Average ）

原理：通过计算窗口内数据的平均值来平滑噪声，适用于快速去除高频噪声。

数据定义

设原始信号为 ，窗口大小为 （奇数），则第 i 个点的平滑值为：

其中 ，边缘点需特殊处理。

步骤：

（1）选择窗口大小：窗口宽度 N=2m+1 （奇数），如5点、7点等。

（2）滑动窗口：对每个数据点 xi ，取其前后各 m 个点，计算均值：

（3）边缘处理：

截断法：舍弃无法构成完整窗口的边缘点，导致输出数据变短。

填充法：用镜像、常数或延拓值填充边缘，保持数据长度。

移动平均算法计算简单，实时性强。但汉斯可能导致峰形展宽，细节丢失；窗口过大易导致信号失真。

参数选择：

噪声频率：高频噪声选择较小窗口（如5点），低频噪声需较大窗口。

信号特征：窗口应小于FBG反射谱主瓣宽度，避免过度平滑。

MATLAB****编程

对每个数据点 ，取其前后各 个点，计算均值：

需处理信号边缘的填充问题。

内部函数：smoothdata(data, 'movmean', N)

1.2 Savitzky-Golay****滤波（ SG 滤波）

原理：基于局部多项式拟合平滑算法，其数学核心为最小二乘拟合，在平滑的同时保留信号高阶特征（如峰形、宽度）。

SG 滤波数学推导

（1）多项式拟合模型

对窗口内每个点 ，假设其满足 k 阶多项式：

其中 是窗口内的局部索引（中心点 ）。

（2）矩阵形式与最小二乘解

设计矩阵：构造范德蒙矩阵 ，维度为 ：

目标向量：窗口内的观测值 。

拟合系数：通过最小二乘法解得：

a= X T X -1 X Ty

平滑值：取中心点 j=0 的拟合值，即 y i = a0 。

（3）卷积核生成

SG滤波可通过预计算卷积系数 \(C\) 实现快速计算：

其中 1 0 ...0 对应 j0 项的系数 a0 。

步骤：

（1）选择参数：

窗口大小 （奇数）。

多项式阶数 （通常2-4阶）。

（2）多项式拟合：对每个窗口内的数据，用最小二乘法拟合多项式：

（3）计算平滑值：取拟合多项式在窗口中心点 i=0 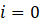的值作为平滑结果。

卷积实现：通过预计算的卷积系数（如SciPy的signal.savgol_filter）快速计算。

优缺点：

优点：保留信号细节，适合处理光谱峰。

缺点：计算量略大；需等间距数据。

参数选择：

窗口大小：通常5-15点，需平衡平滑与细节。

多项式阶数：2或3阶适用于多数光谱数据，高阶易过拟合。

边缘填充

MATLAB的 padarray 函数支持多种填充模式：

'symmetric': 镜像填充（对应Python的reflect）

'replicate': 复制边缘值（对应Python的edge）

'circular': 循环填充

MATLAB****编程

数学原理

对窗口内数据拟合 阶多项式：

通过最小二乘求解系数 并取中心点 的拟合值 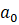作为平滑结果

MATLAB内部函数sgolayfilt函数

1.3****领域平均滤波法（ Adjacent Averaging ）

领域平均滤波法是一种基于局部均值运算的信号平滑方法，通过计算信号中每个数据点领域窗口内数据的平均值来抑制噪声。其核心思想是用局部数据的统计特性（均值）替代原始数据点，从而消除高频噪声，同时保留信号的主要趋势。

数学推导

设原始信号为 ，滤波窗口大小为 （奇数），则第 i 个点的滤波输出 ( yi 定义为：

其中：

i ，即窗口需完全覆盖信号范围。

边缘处理 ：对信号起始和结束的 个点需通过填充（如镜像、常数等）扩展数据。

步骤：

（1）边缘填充策略

镜像填充（'symmetric'）：复制边缘数据的镜像值，减少边界突变。

复制填充（'replicate'）：重复边缘值，适用于平稳信号。

常数填充（'constant'）：以固定值（默认0）填充，需额外参数指定填充值。

（2）窗口大小选择

小窗口，如5点，保留细节大噪声抑制弱。大窗口，如15点，强噪声抑制但可能导致信号失真。

1.4****三种平滑滤波方法对比表

以下是对 移动平均（Moving Average）、Savitzky-Golay滤波（SG滤波） 和 邻域平均滤波（ Adjacent Averaging ） 的详细对比，涵盖数学原理、参数选择、性能特点及适用场景。

|---------------------|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------|
| 对比维度 | 移动平均（ Moving Average ） | Savitzky-Golay 滤波（ SG 滤波） | 邻域平均滤波（ Adjacent Averaging ） |
| 数学原理 | 窗口内数据均值 | 窗口内多项式拟合，取中心点拟合值 | 窗口内数据均值（与移动平均本质相同） |
| 核心参数 | 窗口大小（奇数） | 窗口大小、多项式阶数 | 窗口大小（奇数） |
| 优点 | - 计算简单 - 实时性强 - 适合强噪声抑制 | - 保留信号细节（峰形、宽度） - 适合复杂峰形分析 | - 实现简单 - 与移动平均效果一致 |
| 缺点 | - 峰形展宽 - 高频细节丢失 | - 计算复杂（需多项式拟合）<br>- 参数调整敏感 | - 同移动平均 |
| 适用场景 | - 实时数据处理 - 高频噪声抑制 | - 光谱分析（FBG中心波长检测） - 需要保留峰形特征 | - 通用信号去噪 - 与移动平均应用场景一致 |
| 计算复杂度 | ON⋅W （滑动窗口）或 ON （卷积优化） | (ON⋅W⋅k （多项式拟合， k 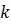为阶数） | ON⋅W （与移动平均相同） |
| 边缘处理策略 | 镜像填充、常数填充、截断 | 同左 | 同左 |
| MATLAB 内置函数 | smoothdata(data, 'movmean', W) | sgolayfilt(data, k, W) | 无直接内置，需自定义（等同于移动平均） |
| 信号保真度 | 低（平滑后信号展宽） | 高（保留高阶特征） | 低（同移动平均） |
| 噪声抑制能力 | 强（适合高斯噪声） | 中（依赖窗口与阶数） | 强（同移动平均） |

数学本质差异

移动平均 vs. 邻域平均：二者数学本质相同，均为窗口内均值计算。差异仅在于实现时的命名习惯（如"邻域平均"更强调局部邻域操作）。

SG 滤波：基于最小二乘多项式拟合，通过保留高阶导数信息（如峰形曲率）实现高保真平滑。

参数选择建议

|-----------|-------------------------|----------------|
| 参数 | 移动平均 / 邻域平均 | SG 滤波 |
| 窗口大小 | 5-25点（噪声越强，窗口越大） | 5-15点（需覆盖主峰宽度） |
| 多项式阶数 | 不适用 | 2-3阶（阶数过高易过拟合） |

适用场景推荐

选择移动平均 / 邻域平均：

实时性要求高（如传感器数据流处理）。

信号特征简单，无需保留高频细节（如温度趋势分析）。

对实时性要求高或噪声简单，可用移动平均。

选择 SG 滤波：

信号峰形关键（如FBG中心波长检测），优先选SG滤波。

光谱分析、色谱峰检测等需保留峰形特征的场景。

信号含复杂高频成分但需抑制随机噪声（如ECG信号去噪）。

边缘处理策略

镜像填充（'symmetric'）：减少边界突变，适合多数信号。

常数填充（'constant'）：适合信号首尾平稳的场景。

截断处理：输出数据变短，适合后续插值。

1.5****自定义函数编码

MATLAB实现

主要代码

clc
close all
clear
% 生成含噪声的正弦信号
t = linspace(0, 10, 1000);
signal = sin(t) + 0.5 * randn(size(t));
% 应用邻域平均滤波
window_size = 15;  % 窗口大小（奇数）
poly_order = 2;
tic;
smoothed_MA = moving_average(signal, window_size, 'symmetric');
elapsedTime = toc;    % 结束计时并返回耗时（秒）
fprintf('moving_average算法执行时间: %.4f 秒\n', elapsedTime);
% 使用Savitzky_Golay算法
tic;
smoothed_SG = Savitzky_Golay(signal, poly_order, window_size, 'symmetric');
elapsedTime = toc;    % 结束计时并返回耗时（秒）
fprintf('Savitzky_Golay算法执行时间: %.4f 秒\n', elapsedTime);
% 使用卷积实现邻域平均算法
tic;
smoothed_AAF = adjacent_averaging_fast(signal, window_size, 'symmetric');
elapsedTime = toc;    % 结束计时并返回耗时（秒）
fprintf('卷积邻域平均算法执行时间: %.4f 秒\n', elapsedTime);
% 绘图对比
figure
hold on
plot(t, signal, 'k', 'LineWidth', 0.5);
plot(t, smoothed_MA, 'r', 'LineWidth', 3);
plot(t, smoothed_SG, 'g', 'LineWidth', 1);
plot(t, smoothed_AAF, 'b--', 'LineWidth', 2);
legend('原始信号（含噪声）', '邻域平均滤波结果','Savitzky-Golay滤波结果','卷积邻域平均滤波结果');
title('邻域平均滤波效果对比');
xlabel('时间'); ylabel('幅值');
hold off

Python实现

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter
import time

# 设置中文字体
# 设置全局字体配置
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题



def moving_average(data, window_size, padding_mode):
    """
    移动平均滤波

    参数:
    data: 输入信号 (1D numpy array)
    window_size: 窗口大小 (必须为奇数)
    padding_mode: 边缘填充模式 ('symmetric', 'edge', 'wrap')

    返回:
    smoothed: 平滑后的信号
    """
    n = len(data)
    m = (window_size - 1) // 2

    # 边缘填充
    padded_data = np.pad(data, m, mode=padding_mode)

    # 初始化平滑结果
    smoothed = np.zeros(n)

    # 滑动窗口计算均值
    for i in range(n):
        window_start = i
        window_end = i + 2 * m + 1  # 注意Python切片不包含结束索引
        smoothed[i] = np.mean(padded_data[window_start:window_end])

    return smoothed


def Savitzky_Golay(data, poly_order, window_size, padding_mode):
    """
    Savitzky-Golay局部多项式拟合滤波

    参数:
    data: 输入信号 (1D numpy array)
    window_size: 窗口大小 (必须为奇数)
    poly_order: 多项式阶数
    padding_mode: 边缘填充模式 ('symmetric', 'edge', 'wrap')

    返回:
    smoothed: 平滑后的信号
    """
    n = len(data)
    m = (window_size - 1) // 2

    # 生成范德蒙矩阵（设计矩阵）
    j = np.arange(-m, m + 1)
    X = np.zeros((window_size, poly_order + 1))
    for p in range(poly_order + 1):
        X[:, p] = j ** p

    # 计算卷积核系数（提取a0）
    C = np.linalg.inv(X.T @ X) @ X.T
    C = C[0, :]

    # 边缘填充
    padded_data = np.pad(data, m, mode=padding_mode)

    # 初始化平滑结果
    smoothed = np.zeros(n)

    # 对每个点应用卷积核
    for i in range(n):
        window = padded_data[i:i + window_size]
        smoothed[i] = np.sum(C * window)

    return smoothed


def adjacent_averaging_fast(data, window_size, padding_mode):
    """
    使用卷积实现邻域平均（高效版）

    参数:
    data: 输入信号 (1D numpy array)
    window_size: 窗口大小 (必须为奇数)
    padding_mode: 边缘填充模式 ('symmetric', 'edge', 'wrap')

    返回:
    smoothed: 平滑后的信号
    """
    # 确保输入是numpy数组
    data = np.asarray(data)

    m = (window_size - 1) // 2

    # 创建卷积核（均匀权重）
    kernel = np.ones(window_size) / window_size

    # 边缘填充
    padded_data = np.pad(data, m, mode=padding_mode)

    # 使用卷积计算平滑结果
    smoothed = np.convolve(padded_data, kernel, mode='valid')

    return smoothed

# 生成含噪声的正弦信号
t = np.linspace(0, 10, 1000)
signal = np.sin(t) + 0.5 * np.random.randn(len(t))

# 应用邻域平均滤波
window_size = 15  # 窗口大小（奇数）
poly_order = 2

# 移动平均滤波
start_time = time.time()
smoothed_MA = moving_average(signal, window_size, 'symmetric')
elapsedTime_MA = time.time() - start_time
print(f'moving_average算法执行时间: {elapsedTime_MA:.4f} 秒')

# Savitzky-Golay滤波
start_time = time.time()
smoothed_SG = Savitzky_Golay(signal, poly_order, window_size, 'symmetric')
elapsedTime_SG = time.time() - start_time
print(f'Savitzky_Golay算法执行时间: {elapsedTime_SG:.4f} 秒')

# 卷积邻域平均滤波
start_time = time.time()
smoothed_AAF = adjacent_averaging_fast(signal, window_size, 'symmetric')
elapsedTime_AAF = time.time() - start_time
print(f'卷积邻域平均算法执行时间: {elapsedTime_AAF:.4f} 秒')

# 绘图对比
plt.figure(figsize=(10, 6))
plt.plot(t, signal, 'k', linewidth=0.5, label='原始信号（含噪声）')
plt.plot(t, smoothed_MA, 'r', linewidth=3, label='邻域平均滤波结果')
plt.plot(t, smoothed_SG, 'g', linewidth=1, label='Savitzky-Golay滤波结果')
plt.plot(t, smoothed_AAF, 'b--', linewidth=2, label='卷积邻域平均滤波结果')
plt.legend()
plt.title('邻域平均滤波效果对比')
plt.xlabel('时间')
plt.ylabel('幅值')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()