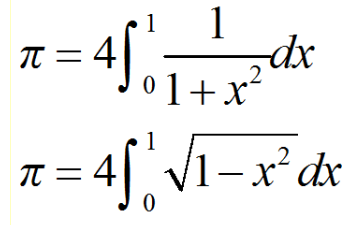一、符号对象的建立
Matlab符号运算特点
·计算以推理方式进行,因此不受计算误差积累所带来的困扰
·符号计算指令的调用比较简单,与数学教科书上的公式相近
Matlab符号运算举例


符号对象与符号表达式
·在进行符号运算时,必须先定义基本的符号对象,可以是符号常量、符号变量、符号表达式等。符号对象是一种数据结构。
符号对象的建立
·符号对象的建立:syms
-syms命令用来建立多个符号变量,格式为:
syms 符号变量1 符号变量2 ... 符号变量n
例:

·符号对象的建立:sym
-sym函数用来建立单个符号变量,一般调用格式为:
符号变量 = sym(x)
参数x可以是一个数或数值矩阵,也可以是字符串
例:

a是符号变量
符号表达式的替换
·用给定的数据替换符号表达式中的指定的符号变量

subs举例



符号表达式的数值化
·对符号求值的命令为vpa,即Variable precision arithmetic

例:

计算极限



上机练习:计算极限


计算导数

例:

上机练习:计算导数


二、符号微积分
计算积分



上机练习:计算积分


符号求和



三、级数求和
Taylor级数展开

例: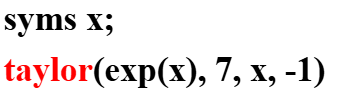

注意:新版本要使用 taylor(f,x,a,'order',n)

代数方程和微分方程求解
·代数方程求解

·微分方程求解

数值积分
(1)自适应Simpson法

功能:采用递推自适应Simpson法计算积分,精度较高,较常使用。求一元函数fun的积分,积分上限和下限分别为a和b,绝对误差为tol,函数fun是待求解的对象,可以是字符串、内联函数、M函数文件名的函数句柄。



(2)梯形法

trapz函数采用梯形法求取数值积分,适用于表格形式定义的函数关系的求定积分问题,求值速度过快,但精度差。其中向量X,Y定义函数关系Y=f(x)。


四、卫星的轨道长度

分析:人造卫星轨道可视为平面上的椭圆,由于地球位于卫星椭圆轨道的一个焦点上,根据近地点距离和远地点距离可分别计算出椭圆长半轴、椭圆半焦距、椭圆短半轴为

五、国土面积的计算



上机作业




六、补选实验